一、什么是数组?
Python 里没有原生的 "数组" 类型,我们通常说的数组操作 指的是numpy库提供的numpy 数组(ndarray)------ 它是专门用来处理数值型数据的 "容器",比 Python 普通列表更高效,支持多维数据和数学运算。
二、准备工作:安装 + 导入 numpy
1. 安装 numpy
打开电脑的命令提示符(Windows)或终端(Mac/Linux),输入以下命令按回车:
python
pip install numpy(如果提示 "pip 不是内部命令",可以先安装 Python 并勾选 "Add Python to PATH")
2. 导入 numpy
使用 numpy 前,需要在代码里 "引入" 它,通常简写为np:
python
import numpy as np # 这行是固定开头,后续用np代替numpy三、数组的形状相关操作
数组的 "形状" 指的是维度大小 (比如一维、二维、三维),用shape属性描述,常见操作有查看形状、修改形状、转置。
1. 查看数组形状(shape 属性)
先创建不同维度的数组,再看形状:
python
# 一维数组(像一条线)
a = np.array([1, 2, 3, 4])
print(a.shape) # 输出:(4,) → 表示一维,有4个元素
# 二维数组(像表格:2行3列)
b = np.array([[1, 2, 3], [4, 5, 6]])
print(b.shape) # 输出:(2, 3) → 2行、3列
# 三维数组(像立方体:2个"2行3列"的表格)
c = np.array([[[1,2,3], [4,5,6]], [[7,8,9], [10,11,12]]])
print(c.shape) # 输出:(2, 2, 3) → 2个表格、每个表格2行3列2. 修改数组形状(reshape 方法)
把数组改成指定形状(注意:元素总数必须匹配!):
python
# 一维数组转二维(4个元素 → 2行2列)
a_reshape = a.reshape(2, 2)
print(a_reshape)
# 输出:
# [[1 2]
# [3 4]]
# 二维数组转一维(6个元素 → 1行)
b_reshape = b.reshape(6,)
print(b_reshape) # 输出:[1 2 3 4 5 6]
# 也可以用-1自动计算维度(比如6个元素转"?行2列")
b_auto = b.reshape(-1, 2)
print(b_auto)
# 输出:
# [[1 2]
# [3 4]
# [5 6]]3. 数组转置(T 属性 /transpose 方法)
转置就是行变列、列变行(主要用于二维数组):
python
b = np.array([[1,2,3], [4,5,6]])
b_T = b.T # 转置
print(b_T)
# 输出:
# [[1 4]
# [2 5]
# [3 6]]四、数组的常见操作
1. 索引与切片(取元素)
和 Python 列表类似,但支持多维索引,简单说:逗号分隔维度,冒号表示 "全部"。
(1)一维数组(和列表一样)
python
a = np.array([1, 2, 3, 4])
print(a[0]) # 取第1个元素 → 1
print(a[1:3]) # 取第2-3个元素 → [2 3]
print(a[-1]) # 取最后1个元素 → 4(2)二维数组(行,列)
python
b = np.array([[1,2,3], [4,5,6]])
print(b[0, 1]) # 取第1行、第2列 → 2
print(b[:, 0]) # 取所有行、第1列 → [1 4]
print(b[1, :]) # 取第2行、所有列 → [4 5 6]2. 基本算术操作
numpy 数组支持逐元素运算,比列表更方便:
python
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# 数组+数字(广播:每个元素都加2)
print(a + 2) # 输出:[3 4 5]
# 数组+数组(对应位置相加)
print(a + b) # 输出:[5 7 9]
# 数组*数组(对应位置相乘)
print(a * b) # 输出:[4 10 18]
# 数组/数字
print(b / 2) # 输出:[2. 2.5 3. ]3. 统计类操作
numpy 提供了很多统计函数(求和、均值、最大 / 最小值等),还能指定 "维度" 计算:
python
b = np.array([[1,2,3], [4,5,6]])
# 全局求和
print(np.sum(b)) # 输出:21(1+2+3+4+5+6)
# 按列求和(axis=0 → 列方向)
print(np.sum(b, axis=0)) # 输出:[5 7 9](1+4, 2+5, 3+6)
# 按行求和(axis=1 → 行方向)
print(np.sum(b, axis=1)) # 输出:[6 15](1+2+3, 4+5+6)
# 均值、最大值、最小值
print(np.mean(b)) # 输出:3.5(21/6)
print(np.max(b)) # 输出:6
print(np.min(b)) # 输出:14. 数组的拼接与分割
(1)拼接(合并数组)
用np.concatenate,指定axis控制方向:
python
b1 = np.array([[1,2], [3,4]])
b2 = np.array([[5,6], [7,8]])
# 垂直拼接(axis=0 → 往下加行)
print(np.concatenate([b1, b2], axis=0))
# 输出:
# [[1 2]
# [3 4]
# [5 6]
# [7 8]]
# 水平拼接(axis=1 → 往右加列)
print(np.concatenate([b1, b2], axis=1))
# 输出:
# [[1 2 5 6]
# [3 4 7 8]](2)分割(拆分数组)
用np.split,指定分割份数或位置:
python
c = np.array([1,2,3,4,5,6])
# 分成2份
print(np.split(c, 2)) # 输出:[array([1,2,3]), array([4,5,6])]
# 按位置分割(在索引2和4处切)
print(np.split(c, [2,4])) # 输出:[array([1,2]), array([3,4]), array([5,6])]五、重点总结
- 数组操作依赖
numpy库,先import numpy as np; - 形状用
shape查看,reshape修改,T转置; - 索引切片:多维用逗号分隔(行,列);
- 算术运算支持逐元素操作,统计函数可指定
axis; - 拼接用
concatenate,分割用split。
小技巧:每次学一个操作,先写小例子运行看结果,比死记硬背更有效!
我们按图片呈现的逻辑顺序(从 "几何类比尝试" 到 "层级嵌套核心方法")来逐一解读:
第一步:最初的几何可视化尝试(三维张量)
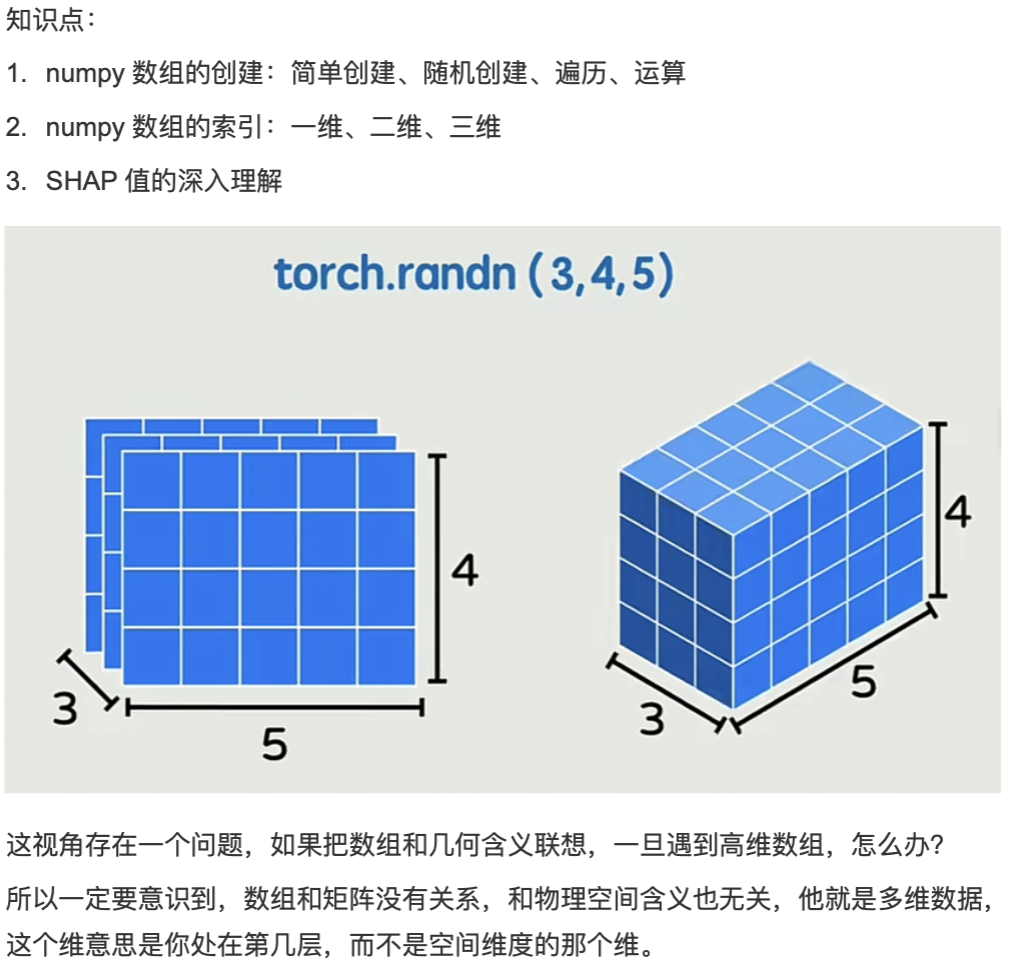
第一张图应该是用立方体 类比三维张量(比如torch.randn(3,4,5)):把三维张量想象成 "长 × 宽 × 高" 的立方体 ------3 个 "切片"(对应第一个维度 3),每个切片是 4 行 5 列的矩阵(对应后两个维度 4、5)。这种方式对三维张量很直观,能快速联想到物理空间的 "立体结构"。
第二步:发现高维张量的理解困境
紧接着的图会指出:当张量维度≥4 时,几何类比失效 (比如四维张量torch.randn(2,3,4,5),无法用物理空间的四维形状联想)。因此需要跳出 "物理空间维度" 的思维,转向 "层级嵌套" 的核心理解方式 。
第三步:层级嵌套的基础 ------ 一维张量
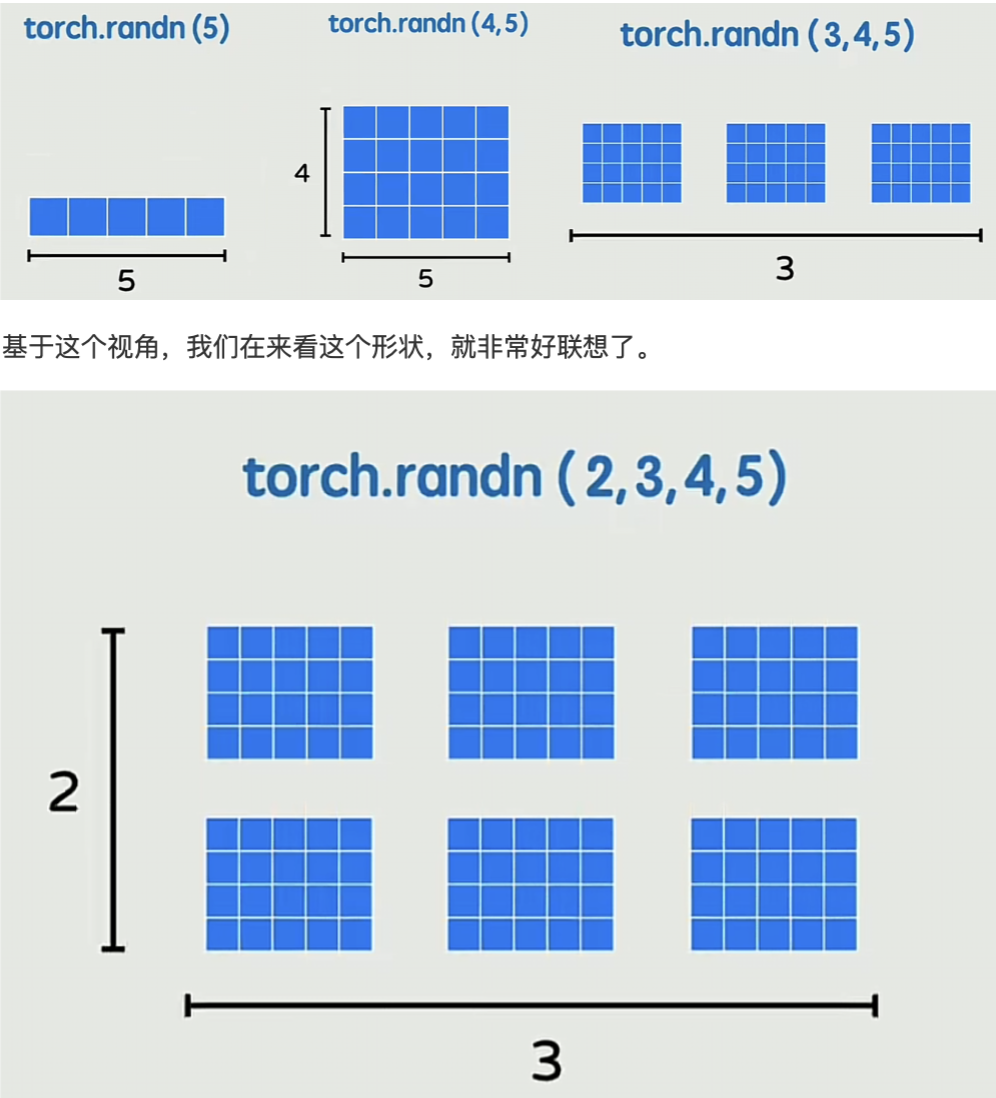
然后是一维张量的解读(如torch.randn(5)):张量的维度是 "从外到内的层级包含关系",一维张量只有1 层结构,直接包含 5 个元素(可视化成 "1 行 5 个独立块"),每个块就是一个数值。
第四步:层级嵌套的延伸 ------ 二维张量
接下来是二维张量(如torch.randn(4,5)):二维张量是2 层嵌套:外层有 4 个 "子结构",每个子结构是 "1 行 5 个元素的一维张量"(可视化成 "4 行 5 列的表格")。这里的 "4" 对应 "外层包含的子结构数量","5" 对应 "每个子结构包含的元素数量"。
第五步:层级嵌套的深化 ------ 三维张量
再到三维张量(如torch.randn(3,4,5)):三维张量是3 层嵌套:最外层有 3 个 "子结构",每个子结构是 "4 行 5 列的二维张量"(可视化成 "3 个并排的 4×5 表格")。第一个维度 "3" 对应 "最外层的子结构数量",后两个维度 "4、5" 对应每个子结构的二维形状。
第六步:层级嵌套的拓展 ------ 四维张量
最后是四维张量(如torch.randn(2,3,4,5)):四维张量是4 层嵌套:最外层有 2 个 "子结构",每个子结构是 "3 个 4×5 表格的三维张量"(可视化成 "2 组堆叠的三维张量")。第一个维度 "2" 对应 "最外层的子结构数量",后三个维度 "3、4、5" 对应每个子结构的三维形状。
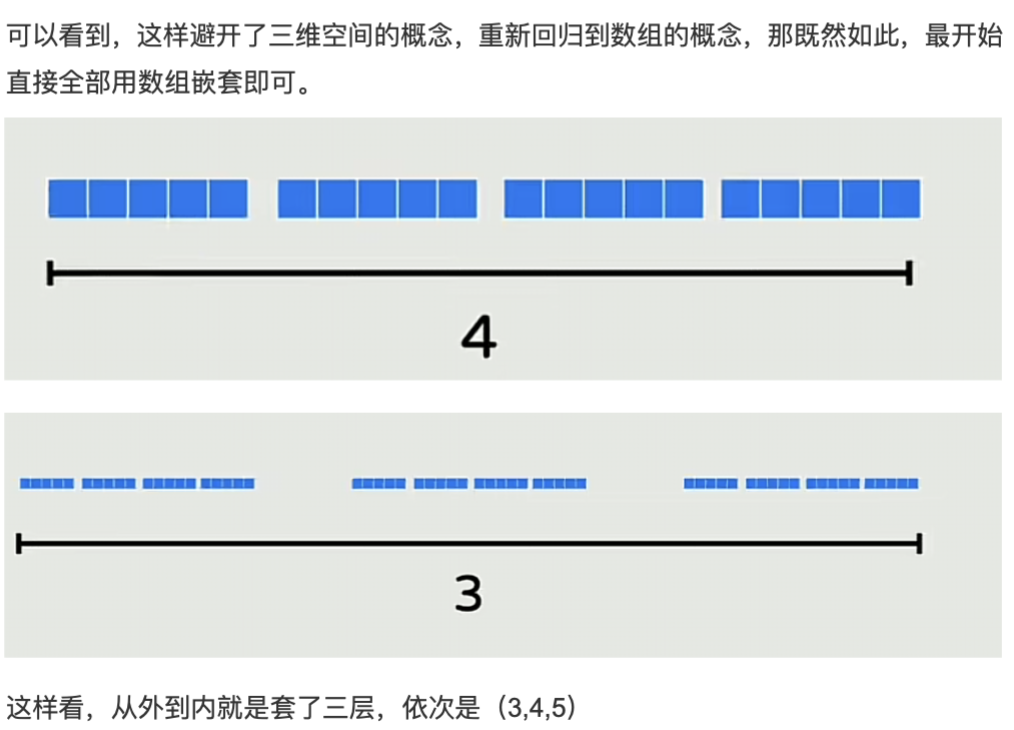
总结:图片传递的核心逻辑
图片从 "几何类比的局限性" 切入,逐步过渡到 **"层级嵌套是理解张量维度的通用方法"**:无论张量有多少维,只需按 "从外到内" 的顺序,把每个维度的数字解读为 "当前层级包含的下一层子结构数量",就能轻松拆解任意维度的张量,彻底解决高维张量的理解难题。
以上是关于PyTorch 张量(Tensor)形状的可视化解读,核心是用 "层级嵌套" 的方式理解多维张量,避免将数组维度与物理空间维度绑定导致的高维理解困难,以下是结构化解读:
1. 核心思路:维度是 "层级嵌套",非物理空间维度
最初用几何立方体(如torch.randn(3,4,5)的立方体)展示三维张量,但该方式会让高维(≥4 维)张量难以联想,因此明确:张量的 "维度" 是层级包含关系(即 "第几层包含多少个下一层结构"),而非物理空间的维度。
2. 不同维度张量的层级理解
以torch.randn生成的张量为例,形状的每个数字对应 "从外到内某一层的包含数量":
- 一维张量(
torch.randn(5)):1 层结构,包含 5 个元素(表现为 1 行 5 个块)。 - 二维张量(
torch.randn(4,5)):2 层嵌套,外层包含 4 个内层结构,每个内层是 "1 行 5 个元素"(表现为 4 行 5 列的矩阵)。 - 三维张量(
torch.randn(3,4,5)):3 层嵌套,外层包含 3 个内层结构,每个内层是 "4 行 5 列的二维张量"(表现为 3 个 "4×5 矩阵")。 - 四维张量(
torch.randn(2,3,4,5)):4 层嵌套,外层包含 2 个内层结构,每个内层是 "3 个 4×5 矩阵的三维张量"(表现为 2 组 "3 个 4×5 矩阵")。
3. 该理解方式的优势
- 规避高维(≥4 维)张量的空间联想困境:无论多少维,只需按 "从外到内的层级包含关系" 拆解即可。
- 清晰对应张量形状的数字含义:张量形状的每个数字,对应从外到内某一层的 "包含数量"(如
torch.randn(a,b,c,d)表示:第 1 层有 a 个,每个包含 b 个第 2 层结构,每个第 2 层结构包含 c 个第 3 层结构,每个第 3 层结构包含 d 个元素)。
numpy数组的创建:简单创建、随即创建、遍历、运算
一、numpy 数组的创建
数组创建是使用 numpy 的第一步,分为简单创建 (手动 / 固定规则)和随机创建(生成随机数数组),咱们一个个讲清楚。
1. 简单创建(手动 / 固定规则)
(1)从 Python 列表 / 元组创建(最基础)
直接用np.array()把列表或元组转成数组,这是最直观的方式:
python
import numpy as np # 先导入numpy,记牢这行!
# 一维数组(从列表创建)
arr1 = np.array([1, 2, 3, 4])
print(arr1) # 输出:[1 2 3 4]
# 二维数组(嵌套列表)
arr2 = np.array([[1, 2], [3, 4]])
print(arr2)
# 输出:
# [[1 2]
# [3 4]]
# 从元组创建(和列表一样)
arr3 = np.array((5, 6, 7))
print(arr3) # 输出:[5 6 7](2)创建特殊用途的数组(常用!)
numpy 提供了快捷函数,直接生成全 0、全 1、等差 / 等比数组,不用手动写列表:
python
# 1. 全0数组:np.zeros(形状)
zero_arr = np.zeros((2, 3)) # 2行3列的全0数组
print(zero_arr)
# 输出:
# [[0. 0. 0.]
# [0. 0. 0.]]
# 2. 全1数组:np.ones(形状)
one_arr = np.ones(4) # 一维、4个元素的全1数组
print(one_arr) # 输出:[1. 1. 1. 1.]
# 3. 单位矩阵(对角线为1,其余为0):np.eye(行数)
eye_arr = np.eye(3) # 3行3列的单位矩阵
print(eye_arr)
# 输出:
# [[1. 0. 0.]
# [0. 1. 0.]
# [0. 0. 1.]]
# 4. 等差数组(类似range):np.arange(起始, 结束, 步长)
arange_arr = np.arange(0, 10, 2) # 从0到10(不含10),步长2
print(arange_arr) # 输出:[0 2 4 6 8]
# 5. 固定个数的等差数组:np.linspace(起始, 结束, 个数)
linspace_arr = np.linspace(0, 1, 5) # 0到1之间生成5个均匀数
print(linspace_arr) # 输出:[0. 0.25 0.5 0.75 1. ]2. 随机创建(生成随机数数组)
用np.random模块,适合模拟数据,记住几个常用函数就行:
python
# 1. 生成[0,1)之间的随机数:np.random.rand(形状)
rand_arr = np.random.rand(2, 2) # 2行2列的随机数(0≤x<1)
print(rand_arr)
# 示例输出(每次运行结果不同):
# [[0.34 0.56]
# [0.12 0.78]]
# 2. 生成标准正态分布随机数(均值0,方差1):np.random.randn(形状)
randn_arr = np.random.randn(3) # 一维、3个元素的正态分布数
print(randn_arr)
# 示例输出:[-0.21 0.53 1.02]
# 3. 生成指定范围的整数:np.random.randint(最小值, 最大值, 形状)
randint_arr = np.random.randint(1, 10, (2, 3)) # 1到9(不含10),2行3列
print(randint_arr)
# 示例输出:
# [[5 3 7]
# [2 8 4]]
# 4. 固定随机种子(让每次运行结果一样,方便调试)
np.random.seed(123) # 种子数随便设,比如123
fixed_rand = np.random.rand(2)
print(fixed_rand) # 每次运行都输出:[0.69646919 0.28613933]二、数组的遍历
遍历就是逐个访问数组元素,一维数组简单,多维数组需要注意维度,咱们从简单到复杂来:
1. 一维数组遍历(和列表一样)
直接用for循环就行:
python
arr = np.array([1, 2, 3, 4])
for num in arr:
print(num) # 依次输出1、2、3、42. 二维数组遍历(按行 / 按元素)
(1)按行遍历(默认)
python
arr2 = np.array([[1, 2], [3, 4]])
for row in arr2:
print("行:", row)
# 输出:
# 行: [1 2]
# 行: [3 4](2)按元素遍历(嵌套循环)
python
for row in arr2:
for num in row:
print(num) # 依次输出1、2、3、4(3)更高效的遍历:np.nditer ()
处理多维数组时,用np.nditer()可以直接遍历所有元素,不用嵌套循环:
python
for num in np.nditer(arr2):
print(num) # 依次输出1、2、3、43. 三维数组遍历(了解即可)
三维数组可以理解为 "多个二维数组",遍历思路类似:
python
arr3 = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
for matrix in arr3: # 先遍历每个二维数组
print("二维数组:")
print(matrix)
for row in matrix: # 再遍历每行
for num in row: # 最后遍历每个元素
print(num)三、数组的运算
numpy 数组的运算比 Python 列表方便太多,支持逐元素运算 、广播机制 和矩阵运算,咱们分清楚:
1. 逐元素运算(对应位置计算)
数组和数组之间,或数组和数字之间,逐个元素计算:
python
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# 数组+数组(对应位置加)
print(a + b) # 输出:[5 7 9]
# 数组-数组(对应位置减)
print(b - a) # 输出:[3 3 3]
# 数组*数组(对应位置乘,不是矩阵乘法!)
print(a * b) # 输出:[4 10 18]
# 数组/数组(对应位置除)
print(b / a) # 输出:[4. 2.5 2. ]
# 数组+数字(每个元素都加)
print(a + 10) # 输出:[11 12 13]
# 数组**2(每个元素平方)
print(a **2) # 输出:[1 4 9]2. 广播机制(不同形状数组的运算)
当两个数组形状不同时,numpy 会自动 "扩展" 小数组,让它们能逐元素运算(前提是维度兼容):
python
# 例子1:一维数组(3个元素)和二维数组(2行3列)运算
a = np.array([1, 2, 3])
b = np.array([[4, 5, 6], [7, 8, 9]])
print(a + b)
# 输出(a被广播成2行3列,和b相加):
# [[ 5 7 9]
# [ 8 10 12]]
# 例子2:数字和数组运算(数字被广播成数组形状)
print(b * 2) # 每个元素乘2,输出:[[ 8 10 12], [14 16 18]]3. 矩阵运算(重点!和逐元素乘区分)
numpy 里矩阵乘法用@或np.dot(),要求第一个数组的列数 = 第二个数组的行数:
python
# 二维数组(矩阵)乘法:(2行3列) × (3行2列) → 2行2列
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[7, 8], [9, 10], [11, 12]])
# 方法1:用@符号
print(A @ B)
# 输出:
# [[ 58 64]
# [139 154]]
# 方法2:用np.dot()
print(np.dot(A, B)) # 和上面结果一样四、重点总结
- 简单创建 :
np.array()(从列表)、np.zeros()/np.ones()(特殊数组)、np.arange()/np.linspace()(等差数组); - 随机创建 :
np.random.rand()([0,1) 随机数)、np.random.randint()(整数)、记得用seed()固定结果; - 遍历 :一维用普通 for 循环,多维用嵌套循环或
np.nditer(); - 运算 :
- 逐元素运算用
+/-/*//; - 矩阵乘法用
@或np.dot(); - 广播机制让不同形状数组能运算(维度要兼容)。
- 逐元素运算用
小技巧 :创建数组后先打印arr.shape看形状,运算前先确认形状是否匹配,避免出错!
numpy数组的索引:一维、二维、三维
数组索引的核心是精准定位并取出数组中的元素,就像从书架上找书:一维是 "找第几层",二维是 "找第几层第几格",三维是 "找哪个书架 + 第几层 + 第几格"。下面从简单到复杂,一步步讲清楚每个维度的索引方法~
一、一维数组索引(最基础,和列表一样)
一维数组是 "一条线",索引规则和 Python 普通列表完全一致:索引从 0 开始,负数表示从末尾倒数。
1. 单个元素索引
python
import numpy as np
arr1 = np.array([10, 20, 30, 40, 50])
print(arr1[0]) # 取第1个元素 → 10(索引0对应第一个元素)
print(arr1[2]) # 取第3个元素 → 30
print(arr1[-1]) # 取最后1个元素 → 50(-1是倒数第一个)
print(arr1[-3]) # 取倒数第3个元素 → 302. 切片索引(取多个元素)
用[起始索引:结束索引:步长],左闭右开(包含起始,不包含结束),省略部分参数有默认值:
- 省略起始:从第一个元素开始;
- 省略结束:到最后一个元素结束;
- 省略步长:步长为 1。
python
arr1 = np.array([10, 20, 30, 40, 50])
print(arr1[1:4]) # 取索引1到3的元素 → [20 30 40](不包含4)
print(arr1[:3]) # 从开头到索引2 → [10 20 30]
print(arr1[2:]) # 从索引2到结尾 → [30 40 50]
print(arr1[::2]) # 步长2,取0、2、4索引 → [10 30 50]
print(arr1[::-1]) # 步长-1,倒序输出 → [50 40 30 20 10]二、二维数组索引(行 + 列,像 Excel 表格)
二维数组是 "表格",索引规则:数组[行索引, 列索引](逗号分隔行和列),同样支持单个元素、切片,甚至 "全行 / 全列"。
1. 先创建一个二维数组
python
arr2 = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 这个数组是3行3列:
# 行0:[1,2,3],行1:[4,5,6],行2:[7,8,9]
# 列0:[1,4,7],列1:[2,5,8],列2:[3,6,9]2. 单个元素索引
python
print(arr2[0, 1]) # 行0(第一行)、列1(第二列)→ 2
print(arr2[2, 0]) # 行2(第三行)、列0(第一列)→ 7
print(arr2[1, -1]) # 行1、最后一列 → 63. 切片索引(取多行 / 多列)
(1)取整行 / 整列
python
print(arr2[1, :]) # 行1(第二行)、所有列 → [4 5 6](冒号表示"全部")
print(arr2[:, 2]) # 所有行、列2(第三列)→ [3 6 9](2)取部分行 + 部分列
python
# 行0到1(前两行)、列1到2(后两列)
print(arr2[0:2, 1:3])
# 输出:
# [[2 3]
# [5 6]]
# 所有行、列0到1(前两列)
print(arr2[:, :2])
# 输出:
# [[1 2]
# [4 5]
# [7 8]](3)不连续索引(花式索引,选特定行 / 列)
用列表指定要取的行或列:
python
print(arr2[[0, 2], :]) # 取行0和行2、所有列 → [[1 2 3], [7 8 9]]
print(arr2[:, [1, 0]]) # 所有行、列1和列0(交换列顺序)→ [[2 1], [5 4], [8 7]]三、三维数组索引(表格组 + 行 + 列,像一沓表格)
三维数组可以理解为 "一沓 Excel 表格",索引规则:数组[表格索引, 行索引, 列索引](三个维度,逗号分隔),先定位 "哪一张表格",再定位 "行和列"。
1. 先创建一个三维数组
python
arr3 = np.array([
[[1, 2], # 表格0:行0[1,2],行1[3,4]
[3, 4]],
[[5, 6], # 表格1:行0[5,6],行1[7,8]
[7, 8]]
])
# 这个数组是:2个表格、每个表格2行2列
# 表格0 → [[1,2],[3,4]]
# 表格1 → [[5,6],[7,8]]2. 单个元素索引
python
print(arr3[0, 1, 0]) # 表格0、行1、列0 → 3
print(arr3[1, 0, 1]) # 表格1、行0、列1 → 6
print(arr3[-1, -1, -1]) # 最后一个表格、最后一行、最后一列 → 83. 切片索引(取多个表格 / 行 / 列)
(1)取整个表格
python
print(arr3[1, :, :]) # 表格1、所有行、所有列 → [[5 6], [7 8]](2)取部分表格 + 部分行 / 列
python
# 所有表格、行0(第一行)、所有列
print(arr3[:, 0, :])
# 输出:[[1 2], [5 6]]
# 表格0到0(只表格0)、行0到1(所有行)、列1(第二列)
print(arr3[0:1, :, 1])
# 输出:[[2 4]]四、核心总结与小技巧
索引维度对应关系:
- 一维:
[元素位置] - 二维:
[行, 列] - 三维:
[表格, 行, 列]维度越多,逗号分隔的索引就越多,本质是 "逐层定位"。
冒号的作用 ::表示 "取当前维度的所有元素",是简化索引的关键。
小练习(巩固理解):对下面的三维数组,取出 "表格 1 的行 1 列 0 元素" 和 "所有表格的列 1 元素":
python
arr = np.array([[[10,20],[30,40]], [[50,60],[70,80]]])
# 答案:arr[1,1,0] → 70;arr[:,:,1] → [[20,40],[60,80]]避坑提醒:索引永远从 0 开始!比如 "第二行" 是索引 1,不是 2,刚开始容易混淆,多敲代码验证就记住了~
如果某个索引写法看不懂,就把数组 "拆解开" 看:比如三维数组arr3[0,1,0],先看arr3[0]是表格 0,再看arr3[0][1]是表格 0 的行 1,最后看arr3[0][1][0]就是行 1 列 0 的元素,一步步来就不会乱啦~
如何在实际项目中运用numpy数组的索引技巧?
numpy 数组索引不是单纯的 "取元素",而是实际项目中数据筛选、局部操作、特征提取的核心工具。下面结合数据分析、图像处理、机器学习 3 个常见场景,讲清楚索引技巧的实战用法,每个例子都配具体代码和思路,你能直接参考~
一、场景 1:数据分析 ------ 筛选和提取关键数据
实际做数据分析时,常需要从表格型数据(二维数组)中提取特定行 / 列、筛选符合条件的数据,这时候索引就是 "数据筛选器"。
案例:销售数据处理
假设我们有一份销售数据(二维数组),每行是 "日期、销售额、销量、客单价",共 4 列:
python
import numpy as np
# 销售数据:5天数据,列=[日期(简化为数字), 销售额, 销量, 客单价]
sales_data = np.array([
[1, 2000, 50, 40],
[2, 3000, 60, 50],
[3, 1500, 30, 50],
[4, 4000, 80, 50],
[5, 2500, 55, 45]
])1. 提取特定列(特征选择)
比如只需要 "销售额" 和 "销量" 列(第 2、3 列,索引 1、2):
python
# 用切片/花式索引取列
sales_core = sales_data[:, [1, 2]] # 所有行,列1和列2
print(sales_core)
# 输出:
# [[2000 50]
# [3000 60]
# [1500 30]
# [4000 80]
# [2500 55]]2. 筛选符合条件的行(条件筛选)
比如筛选 "销量> 50" 的行(布尔索引):
python
# 先做条件判断,得到布尔数组
mask = sales_data[:, 2] > 50 # 销量列(索引2)>50的位置为True
# 用布尔数组取行
high_sales = sales_data[mask]
print(high_sales)
# 输出(销量>50的行):
# [[2 3000 60 50]
# [4 4000 80 50]
# [5 2500 55 45]]3. 提取特定位置的数值(计算指标)
比如取 "销售额最高的那天的客单价":
python
# 先找销售额列(索引1)的最大值索引
max_sales_idx = np.argmax(sales_data[:, 1])
# 用索引取对应行的客单价(索引3)
max_price = sales_data[max_sales_idx, 3]
print(f"销售额最高那天的客单价:{max_price}") # 输出:50二、场景 2:图像处理 ------ 像素操作与图像裁剪
图像在 numpy 中是三维数组 (高度 × 宽度 × 通道,比如 RGB 图像是(height, width, 3)),索引能直接操作像素或裁剪图像。
案例:图像局部修改与裁剪
假设我们有一张 200×200 的 RGB 图像(简化为数组演示):
python
# 模拟创建200×200的RGB图像(三维数组:200行×200列×3通道)
img = np.random.randint(0, 255, (200, 200, 3)) # 像素值0-255
print(img.shape) # 输出:(200, 200, 3)1. 裁剪图像(提取局部区域)
比如裁剪左上角 100×100 的区域(常用的图像预处理步骤):
python
# 取前100行、前100列、所有通道
img_crop = img[:100, :100, :]
print(img_crop.shape) # 输出:(100, 100, 3)2. 修改特定区域的像素(比如加红色滤镜)
比如把图像右下角 100×100 的区域改成红色(R 通道设为 255):
python
# 右下角:行100-200,列100-200,R通道(索引0)设为255
img[100:, 100:, 0] = 255
# 此时img的右下角区域R通道全红,G/B通道不变3. 提取单通道(比如只看红色通道)
python
red_channel = img[:, :, 0] # 所有行、所有列、R通道(索引0)
print(red_channel.shape) # 输出:(200, 200)(二维灰度图)三、场景 3:机器学习 ------ 数据预处理与样本提取
机器学习中,数据集通常是二维数组(样本数 × 特征数),索引用于划分训练集 / 测试集、提取特定类别样本等。
案例:数据集划分与类别筛选
假设我们有 100 个样本的数据集,每行是 "特征 1、特征 2、标签(0/1)":
python
# 模拟数据集:100个样本,2个特征+1个标签
X_y = np.random.rand(100, 3) # 特征随机,标签最后一列(简化为0/1)
X_y[:, 2] = np.random.randint(0, 2, 100) # 标签列设为0或11. 分离特征和标签(特征矩阵 X,标签向量 y)
python
X = X_y[:, :2] # 所有样本,前2列是特征
y = X_y[:, 2] # 所有样本,最后1列是标签
print(X.shape) # 输出:(100, 2)
print(y.shape) # 输出:(100,)2. 划分训练集和测试集(前 80 个样本训练,后 20 个测试)
python
X_train = X[:80] # 前80个样本的特征
y_train = y[:80] # 前80个样本的标签
X_test = X[80:] # 后20个样本的特征
y_test = y[80:] # 后20个样本的标签3. 提取特定类别的样本(比如只取标签为 1 的样本)
python
# 布尔索引筛选标签为1的样本
class1_samples = X[y == 1]
print(f"标签为1的样本数:{class1_samples.shape[0]}")四、实战索引技巧总结
- 先看形状再索引 :用
arr.shape确认数组维度,避免索引维度错误(比如二维数组用三个索引); - 布尔索引是筛选核心:项目中筛选条件(比如销量 > 50、标签 = 1)优先用布尔索引,直观且高效;
- 花式索引(列表索引)用于选不连续列 / 行 :比如取第 1、3 列特征,用
[:, [0,2]]; - 三维数组按 "层→行→列" 索引:图像处理中记住 "高度(行)、宽度(列)、通道" 的顺序。
小建议
实际项目中不用死记所有索引写法,遇到需求时:
① 明确 "要取什么数据"(比如 "所有销量 > 50 的行");
② 拆解步骤(先定位行 / 列,再用对应索引);
③ 先打印数组形状,再小范围测试索引(比如先取前 5 行试试),慢慢就熟练了~
SHAP值的深入了解
SHAP 值是一种基于博弈论的模型解释方法,核心是量化每个特征对单个预测结果的贡献------ 简单说,它能告诉我们 "模型预测结果中,每个特征分别贡献了多少(正 / 负)",让复杂模型(比如树模型、神经网络)的预测变得可解释。
一、什么是 SHAP 值?
SHAP 值的本质是Shapley 值在机器学习模型解释中的应用。Shapley 值来自博弈论,用来解决 "多人合作博弈中,如何公平分配总收益给每个参与者" 的问题;对应到机器学习中:
- "博弈":模型预测一个样本的结果(比如预测 "用户是否会购买商品");
- "参与者":每个输入特征(比如用户年龄、消费金额、浏览时长);
- "总收益":模型的预测值与基准值(比如所有样本的平均预测值)的差值;
- "SHAP 值":每个特征对这个差值的贡献度(正贡献 = 让预测值变大,负贡献 = 让预测值变小)。
二、SHAP 值的核心思想:公平分配特征贡献
要计算某个特征的 SHAP 值,需要考虑该特征在所有可能的特征组合中的 "边际贡献",然后取平均值。举个简单例子:
假设模型预测用户 A 的 "购买概率" 是 80%,所有用户的平均购买概率(基准值)是 50%,那么 "总贡献" 是 80%-50%=30%。现在有两个特征:年龄(25 岁)和月消费(5000 元),要分配这 30% 的贡献:
- 只有 "年龄" 时:模型预测购买概率 60% → 年龄的边际贡献 = 60%-50%=10%;
- 只有 "月消费" 时:模型预测购买概率 70% → 月消费的边际贡献 = 70%-50%=20%;
- 同时有 "年龄 + 月消费" 时:模型预测 80% → 年龄的边际贡献 = 80%-70%=10%,月消费的边际贡献 = 80%-60%=20%;
- 计算 SHAP 值(平均边际贡献) :
- 年龄的 SHAP 值 =(10% + 10%)/2 = 10%;
- 月消费的 SHAP 值 =(20% + 20%)/2 = 20%;最终:50%(基准) + 10%(年龄) + 20%(月消费) = 80%(预测值),完美分配!
三、SHAP 值的关键性质
- 加和性:所有特征的 SHAP 值之和 = 模型预测值 - 基准值(保证贡献分配无遗漏、无重复);
- 公平性:每个特征的贡献是其在所有特征组合中的平均边际贡献,符合博弈论的 "公平分配" 原则;
- 一致性:如果一个特征在所有模型中对预测的影响更大,它的 SHAP 值也会更大(不会出现矛盾)。
四、SHAP 的常见解释方法与可视化
SHAP 库(shap)提供了丰富的可视化工具,能直观展示特征贡献,下面结合实际例子(用树模型预测房价)讲常用方法:
1. 安装 SHAP 库
python
pip install shap2. 基础示例:用 SHAP 解释 XGBoost 模型
python
import shap
import xgboost as xgb
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
# 加载数据(糖尿病数据集,预测疾病进展)
data = load_diabetes()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)
# 训练XGBoost模型
model = xgb.XGBRegressor(n_estimators=100, learning_rate=0.1)
model.fit(X_train, y_train)
# 初始化SHAP解释器(树模型用TreeExplainer,效率高)
explainer = shap.TreeExplainer(model)
# 计算测试集的SHAP值
shap_values = explainer.shap_values(X_test)3. 核心可视化图表
(1)Summary Plot(摘要图)
展示所有特征的 SHAP 值分布,能看出特征的重要性和对预测的影响方向:
python
shap.summary_plot(shap_values, X_test, feature_names=data.feature_names)- 横轴:SHAP 值(正 = 增加预测值,负 = 降低预测值);
- 纵轴:特征(按重要性排序,越上面越重要);
- 颜色:特征值大小(比如红色 = 高值,蓝色 = 低值)。比如 "bmi(体重指数)" 特征,红色点(高 bmi)的 SHAP 值为正,说明高 bmi 会让疾病进展风险增加。
(2)Force Plot(力图)
解释单个样本的预测结果,展示每个特征的贡献:
python
# 解释第一个测试样本
shap.force_plot(explainer.expected_value, shap_values[0], X_test[0], feature_names=data.feature_names)- 中间基准线:模型的平均预测值(expected_value);
- 左右箭头:特征的贡献方向(红色 = 推高预测值,蓝色 = 拉低预测值);
- 数值:每个特征的 SHAP 值大小。比如第一个样本中,"s5(血糖相关)" 的 SHAP 值为正,让预测值从基准线上升,"age(年龄)" 的 SHAP 值为负,让预测值下降。
(3)Dependency Plot(依赖图)
展示单个特征的 SHAP 值与特征值的关系,能发现特征的非线性影响或交互作用:
python
shap.dependency_plot("bmi", shap_values, X_test, feature_names=data.feature_names)- 横轴:特征值(比如 bmi 的大小);
- 纵轴:该特征的 SHAP 值;
- 颜色:另一个特征(比如 s5)的取值,可观察特征间的交互(比如高 bmi + 高 s5 时,SHAP 值增长更快)。
五、SHAP 值的适用场景
- 模型解释:解释单个预测结果(比如 "为什么这个用户被判定为高风险?");
- 特征重要性排序:SHAP 值的绝对值越大,特征越重要(比传统的 "特征重要性" 更可靠);
- 发现特征交互:通过依赖图或 SHAP 交互值,找到特征间的协同 / 抑制作用;
- 模型调试:发现模型的偏见(比如 "性别" 特征对贷款审批的不合理贡献);
- 特征选择:保留 SHAP 值大的特征,简化模型同时保证性能。
六、SHAP 的局限性
- 计算成本:对复杂模型(比如深度学习)或大样本,计算 SHAP 值可能很慢(树模型有高效的 TreeExplainer,其他模型可用 KernelExplainer 但速度慢);
- 解释复杂度:高维数据的 SHAP 值可视化和解读仍有难度;
- 依赖模型:SHAP 值是对 "模型预测" 的解释,不是对 "真实因果关系" 的解释(比如特征相关可能导致 SHAP 值误导)。
七、核心总结
- SHAP 值的本质是博弈论的 Shapley 值在模型解释中的应用,核心是 "公平分配每个特征对预测的贡献";
- 关键性质是加和性(所有 SHAP 值之和 = 预测值 - 基准值);
- 实用价值是让黑箱模型可解释,支持单个预测和全局特征分析;
- 上手建议:先从树模型(XGBoost/LightGBM)+ TreeExplainer 开始,用可视化工具直观理解,再逐步扩展到其他模型。
SHAP 值计算的核心步骤是:
训练模型 → 初始化对应解释器 → 计算 SHAP 值 → 可视化解释
树模型优先用TreeExplainer(速度最快、效果最好),其他模型选择对应解释器即可。重点通过可视化理解特征贡献,而不是死记公式~
第一步:安装必要库
先确保安装了shap、xgboost、scikit-learn和numpy:

第二步:完整代码实现
python
# 1. 导入库
import shap
import xgboost as xgb
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 2. 加载数据集(糖尿病数据集:预测疾病进展程度)
data = load_diabetes()
X = data.data # 特征矩阵(10个特征:年龄、BMI、血糖等)
y = data.target # 标签(疾病进展值,连续型)
feature_names = data.feature_names # 特征名称(方便后续解释)
# 3. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42 # 固定随机种子,结果可复现
)
# 4. 训练XGBoost回归模型
model = xgb.XGBRegressor(
n_estimators=100, # 树的数量
learning_rate=0.1, # 学习率
random_state=42
)
model.fit(X_train, y_train)
# 验证模型效果(可选)
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"模型测试集MSE:{mse:.2f}")
# 5. 初始化SHAP解释器(树模型专用TreeExplainer)
explainer = shap.TreeExplainer(model) # 传入训练好的模型
# 6. 计算SHAP值(对测试集样本)
shap_values = explainer.shap_values(X_test)
# shap_values.shape = (测试集样本数, 特征数) → 每个样本的每个特征对应一个SHAP值
# 7. 查看关键信息
print(f"\n模型基准值(所有样本的平均预测值):{explainer.expected_value:.2f}")
print(f"SHAP值数组形状:{shap_values.shape}") # 比如(89,10):89个测试样本,10个特征
print(f"第一个测试样本的SHAP值:{shap_values[0]}") # 第一个样本的10个特征的SHAP值
# 8. SHAP值可视化(核心步骤)
## (1)Summary Plot:全局特征贡献(最常用)
shap.summary_plot(shap_values, X_test, feature_names=feature_names)
## (2)Force Plot:单个样本的预测解释(比如第一个测试样本)
# 生成HTML格式的力图(更清晰)
shap_html = shap.force_plot(
explainer.expected_value, # 基准值
shap_values[0], # 第一个样本的SHAP值
X_test[0], # 第一个样本的特征值
feature_names=feature_names,
out_file="shap_force_plot.html" # 保存为HTML文件
)
print("\n单个样本解释图已保存为shap_force_plot.html,可在浏览器打开查看")
## (3)Dependency Plot:单个特征的SHAP值与特征值的关系(比如BMI特征)
shap.dependency_plot(
"bmi", # 要分析的特征名称
shap_values,
X_test,
feature_names=feature_names
)代码关键解释
SHAP 值的核心输出:
explainer.expected_value:模型的基准值(所有训练样本的平均预测值,对应之前例子中的 "平均奖金""平均评分");shap_values:二维数组,每行是一个样本的所有特征的 SHAP 值,所有特征的 SHAP 值之和 = 模型预测值 - 基准值(加和性验证)。
比如第一个测试样本:
python
sample_pred = model.predict(X_test[0].reshape(1,-1))[0] # 模型对第一个样本的预测值
shap_sum = np.sum(shap_values[0]) # 第一个样本的SHAP值总和
print(f"预测值:{sample_pred:.2f}")
print(f"基准值 + SHAP总和:{explainer.expected_value + shap_sum:.2f}")两者结果完全一致,验证了 SHAP 值的加和性。
可视化结果解读:
- Summary Plot:纵轴是特征(按重要性排序),横轴是 SHAP 值(正 = 增加预测值,负 = 降低预测值),颜色越深表示特征值越大。比如 "BMI" 特征红色点(高 BMI)的 SHAP 值为正,说明高 BMI 会让疾病进展值升高;
- Force Plot :打开
shap_force_plot.html,能看到每个特征对第一个样本预测的 "推动作用"(红色推高预测值,蓝色拉低); - Dependency Plot:展示 "BMI 特征值" 和 "BMI 的 SHAP 值" 的关系,可观察特征的非线性影响(比如 BMI 越高,SHAP 值增长越快)。
其他模型的 SHAP 值计算
如果用线性模型 (比如LinearRegression),改用shap.LinearExplainer:
python
from sklearn.linear_model import LinearRegression
linear_model = LinearRegression()
linear_model.fit(X_train, y_train)
explainer = shap.LinearExplainer(linear_model, X_train) # 传入模型和训练数据
shap_values = explainer.shap_values(X_test)如果用深度学习模型 (比如 TensorFlow/Keras),改用shap.DeepExplainer(需传入模型和背景数据):
python
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 构建简单DNN模型
dnn_model = Sequential([
Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
Dense(32, activation='relu'),
Dense(1)
])
dnn_model.compile(optimizer='adam', loss='mse')
dnn_model.fit(X_train, y_train, epochs=50, verbose=0)
# 初始化DeepExplainer(背景数据用训练集的子集)
background = X_train[np.random.choice(X_train.shape[0], 100, replace=False)]
explainer = shap.DeepExplainer(dnn_model, background)
shap_values = explainer.shap_values(X_test)除了XGBoost,还有哪些模型可以用于计算SHAP值?
SHAP 值的计算几乎支持所有常见的机器学习模型,不同模型只需搭配对应的 SHAP 解释器即可。下面按模型类型分类,列出常用模型及对应的 SHAP 使用方式,附简单代码示例,新手也能轻松上手~
一、树模型家族(最适配 SHAP,效率最高)
除了 XGBoost,所有基于树的模型都能用shap.TreeExplainer(专门优化,计算超快),包括:
1. LightGBM(轻量级梯度提升树)
python
import shap
import lightgbm as lgb
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
data = load_diabetes()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)
# 训练LightGBM模型
model = lgb.LGBMRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 计算SHAP值
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test)
# 可视化
shap.summary_plot(shap_values, X_test, feature_names=data.feature_names)2. CatBoost(处理类别特征友好的梯度提升树)
python
import shap
from catboost import CatBoostRegressor
# 训练CatBoost模型
model = CatBoostRegressor(n_estimators=100, random_state=42, verbose=0)
model.fit(X_train, y_train)
# 计算SHAP值
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test)3. scikit-learn 树模型(随机森林、决策树等)
python
import shap
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
# 训练随机森林模型
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X_train, y_train)
# 计算SHAP值
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test)二、线性模型(逻辑回归、线性回归等)
scikit-learn 的线性模型用shap.LinearExplainer(基于线性模型的数学性质,解释直接):
python
import shap
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.datasets import load_breast_cancer
# 以分类任务为例(乳腺癌数据集)
data = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2)
# 训练逻辑回归模型
model = LogisticRegression(max_iter=1000, random_state=42)
model.fit(X_train, y_train)
# 计算SHAP值
explainer = shap.LinearExplainer(model, X_train) # 需传入训练数据做背景
shap_values = explainer.shap_values(X_test)
# 可视化
shap.summary_plot(shap_values, X_test, feature_names=data.feature_names)三、深度学习模型(TensorFlow/Keras、PyTorch)
深度学习模型用shap.DeepExplainer(适配 TensorFlow/Keras)或shap.GradientExplainer(更通用,支持 PyTorch):
1. TensorFlow/Keras 模型
python
import shap
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
# 构建简单DNN模型
model = Sequential([
Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
Dense(32, activation='relu'),
Dense(1) # 回归任务
])
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=20, verbose=0)
# 初始化DeepExplainer(需背景数据,取训练集子集)
background = X_train[tf.random.uniform((100,), 0, X_train.shape[0], dtype=tf.int32)]
explainer = shap.DeepExplainer(model, background)
# 计算SHAP值
shap_values = explainer.shap_values(X_test)2. PyTorch 模型
python
import shap
import torch
import torch.nn as nn
# 定义PyTorch模型
class SimpleNN(nn.Module):
def __init__(self, input_dim):
super().__init__()
self.fc1 = nn.Linear(input_dim, 64)
self.fc2 = nn.Linear(64, 32)
self.fc3 = nn.Linear(32, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
return self.fc3(x)
model = SimpleNN(X_train.shape[1])
# 假设已训练模型(省略训练代码)
# 用GradientExplainer
background = torch.tensor(X_train[:100], dtype=torch.float32)
explainer = shap.GradientExplainer((model, model.fc1), background)
shap_values = explainer.shap_values(torch.tensor(X_test, dtype=torch.float32))四、通用黑箱模型(SVM、KNN、任意自定义模型)
对于 SHAP 没有专门优化的模型(如 SVM、KNN、XGBoost 之外的集成模型),用shap.KernelExplainer(基于核方法,通用但速度较慢,适合小样本):
python
import shap
from sklearn.svm import SVR
from sklearn.neighbors import KNeighborsRegressor
# 训练SVM模型
model = SVR(kernel='rbf')
model.fit(X_train, y_train)
# 初始化KernelExplainer(需背景数据,取训练集子集)
background = shap.sample(X_train, 100) # 随机选100个样本做背景
explainer = shap.KernelExplainer(model.predict, background)
# 计算SHAP值(测试集取前50个样本,避免速度过慢)
shap_values = explainer.shap_values(X_test[:50])五、总结:不同模型对应的 SHAP 解释器
| 模型类型 | 推荐解释器 | 特点 |
|---|---|---|
| XGBoost/LightGBM/CatBoost/ 随机森林 | shap.TreeExplainer |
速度最快,效果最好 |
| 线性回归 / 逻辑回归 | shap.LinearExplainer |
基于数学解析,解释直观 |
| TensorFlow/Keras 模型 | shap.DeepExplainer |
适配深度学习,需背景数据 |
| PyTorch 模型 | shap.GradientExplainer |
通用深度学习解释器 |
| SVM/KNN/ 其他黑箱模型 | shap.KernelExplainer |
通用但速度慢,适合小样本 |
小建议:优先用模型专属的解释器(如树模型用 TreeExplainer),速度和效果都优于通用解释器;如果是小众模型,再用 KernelExplainer~
用代码实现SHAP值的计算时,需要注意哪些细节?
用代码实现 SHAP 值计算时,很多细节会影响结果的准确性、效率甚至正确性,尤其对新手来说,稍不注意就容易踩坑。下面梳理核心细节和避坑点,结合代码示例说明:
一、解释器选择:必须匹配模型类型
SHAP 针对不同模型设计了专属解释器,选错解释器会导致计算错误或效率极低:
- 树模型(XGBoost/LightGBM/ 随机森林) :必须用
shap.TreeExplainer(基于树结构优化,速度快、结果准),别用通用的KernelExplainer(慢且没必要); - 线性模型(LinearRegression/LogisticRegression) :用
shap.LinearExplainer(利用线性模型的数学性质,直接解析计算); - 深度学习模型(Keras/PyTorch) :用
shap.DeepExplainer(Keras)或shap.GradientExplainer(PyTorch); - 其他黑箱模型(SVM/KNN) :只能用
shap.KernelExplainer(通用但效率低)。
反例 :给 XGBoost 模型用KernelExplainer:
python
# 错误示范:树模型用KernelExplainer(速度慢10倍+)
explainer = shap.KernelExplainer(model.predict, background_data) # 不推荐
# 正确示范:
explainer = shap.TreeExplainer(model) # 速度快、结果准二、背景数据(Background Data)的设置
DeepExplainer/KernelExplainer/LinearExplainer需要背景数据(代表 "基准分布"),选得不好会影响 SHAP 值的解释性:
- 背景数据的作用 :SHAP 值的基准(
explainer.expected_value)是模型对背景数据的平均预测值,背景数据应代表 "典型样本"; - 选择原则:
- 优先用训练集的随机子集(比如 100-500 个样本),避免用全量训练集(内存爆炸);
- 不要用测试集(数据泄露风险);
- 样本数:
KernelExplainer用 100-200 个足够(太多会卡死),DeepExplainer用 100-1000 个。
正确示例:
python
# 从训练集随机选100个样本做背景
background = shap.sample(X_train, 100, random_state=42)
explainer = shap.DeepExplainer(model, background) # 深度学习模型三、数据预处理:必须与模型训练时一致
SHAP 值是基于 "模型输入" 计算的,如果预处理(缩放、编码)和训练模型时不一致,结果会完全错误:
- 比如 :训练模型时对特征做了
StandardScaler,计算 SHAP 时必须用相同的 scaler 处理测试集; - 类别特征:如果模型训练时用了 OneHotEncoder/LabelEncoder,SHAP 的输入也要保持一致。
正确示例:
python
from sklearn.preprocessing import StandardScaler
# 训练模型时的预处理
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
model.fit(X_train_scaled, y_train)
# 计算SHAP时,测试集必须用相同的scaler转换
X_test_scaled = scaler.transform(X_test) # 用transform,不是fit_transform!
shap_values = explainer.shap_values(X_test_scaled)四、注意 SHAP 值的维度(分类任务 vs 回归任务)
- 回归任务 :SHAP 值是二维数组
(样本数, 特征数); - 分类任务 :
- 二分类:如果模型输出概率,SHAP 值可能是
(样本数, 特征数)(对应正类); - 多分类:SHAP 值是三维数组
(类别数, 样本数, 特征数),需指定解释哪个类别。
- 二分类:如果模型输出概率,SHAP 值可能是
示例(多分类任务):
python
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
data = load_iris()
model = RandomForestClassifier()
model.fit(X_train, y_train)
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test)
print(shap_values.shape) # (3, 30, 4) → 3个类别、30个样本、4个特征
# 解释类别0的SHAP值
shap.summary_plot(shap_values[0], X_test) 五、计算效率:避免不必要的耗时
KernelExplainer:速度极慢,仅用于小样本(测试集≤100 个样本),别直接跑全量测试集;TreeExplainer:虽然快,但如果模型有上万棵树,计算也会慢,可限制模型的n_estimators;- 批量计算:对大样本,可分批计算 SHAP 值(比如每次算 1000 个样本)。
示例(分批计算):
python
# 对大测试集分批计算SHAP值
shap_values_list = []
batch_size = 1000
for i in range(0, len(X_test), batch_size):
batch = X_test[i:i+batch_size]
shap_batch = explainer.shap_values(batch)
shap_values_list.append(shap_batch)
shap_values = np.concatenate(shap_values_list)六、可视化的细节:让结果更易读
必须指定feature_names:否则可视化图里的特征会显示为 "Feature 0/Feature 1",无法解读;
Force Plot的查看方式:
- Jupyter Notebook 中可直接显示:
shap.force_plot(...); - 普通 Python 脚本中需保存为 HTML 文件,再用浏览器打开;
Summary Plot的类型 :分类任务可指定plot_type="bar"看特征重要性,或plot_type="dot"看分布。
示例:
python
# 指定特征名称,可视化更清晰
shap.summary_plot(shap_values, X_test, feature_names=data.feature_names)
# 保存Force Plot到HTML
shap.force_plot(
explainer.expected_value,
shap_values[0],
X_test[0],
feature_names=data.feature_names,
out_file="shap_force.html"
)七、验证 SHAP 值的正确性:加和性检查
SHAP 值的核心性质是 **"所有特征的 SHAP 值之和 = 模型预测值 - 基准值"**,可通过代码验证:
python
# 取第一个测试样本
sample_pred = model.predict(X_test[0].reshape(1, -1))[0] # 模型预测值
shap_sum = np.sum(shap_values[0]) # 该样本的SHAP值总和
base_value = explainer.expected_value # 基准值
# 验证:预测值 ≈ 基准值 + SHAP值总和(允许微小浮点误差)
assert np.isclose(sample_pred, base_value + shap_sum), "SHAP值计算错误!"
print(f"预测值:{sample_pred:.2f}, 基准值+SHAP总和:{base_value + shap_sum:.2f}")八、随机种子:保证结果可复现
SHAP 的部分操作(如背景数据采样、模型训练)涉及随机过程,需固定随机种子:
python
import numpy as np
import random
import shap
# 固定全局随机种子
np.random.seed(42)
random.seed(42)
shap.random.seed(42)
# 模型训练时也固定种子
model = xgb.XGBRegressor(random_state=42)九、内存管理:避免 OOM(内存溢出)
- 处理超大样本时,不要一次性计算所有 SHAP 值(比如 10 万样本);
- 可视化时,
summary_plot可限制样本数(比如shap.summary_plot(shap_values[:1000], ...))。
总结:关键细节清单
- 解释器与模型类型严格匹配;
- 背景数据选训练集子集,数量适中;
- 预处理与模型训练时完全一致;
- 注意分类 / 回归任务的 SHAP 值维度差异;
- 对慢解释器(KernelExplainer)限制样本数;
- 可视化时指定
feature_names; - 用加和性验证 SHAP 值正确性;
- 固定随机种子保证可复现;
- 大样本分批处理,避免内存溢出。
这些细节能帮你避开 90% 的坑,确保 SHAP 值计算准确、高效~
通俗化理解 SHAP 值
用两个生活中最常见的场景 ------"团队项目分红" 和 "餐厅评分",就能把 SHAP 值讲得明明白白,全程没有专业术语,看完就懂!
场景 1:团队项目分红(最贴合 SHAP 核心逻辑)
SHAP 值的本质是 "公平分配贡献",这和 "团队做项目拿奖金,怎么分给每个人" 完全一样 ------ 对应到模型解释,就是 "多个特征(团队成员)共同产生预测结果(项目奖金),SHAP 值就是每个特征(成员)该得的'公平功劳'"。
具体例子:
假设你们公司有个 "项目奖金池",规则是:
- 基准奖金:所有项目的平均奖金是 5000 元(对应模型的 "基准值"------ 所有样本的平均预测值);
- 你们团队的奖金:因为项目做得好,拿到了 8000 元(对应模型的 "预测值"------ 某个样本的具体预测结果);
- 需要分配的额外奖金:8000 - 5000 = 3000 元(对应 "预测值 - 基准值"------ 这个样本和平均水平的差距,也是所有特征要分配的 "总贡献");
- 团队成员(对应模型的 "特征"):4 个人 ------A(需求分析)、B(代码开发)、C(测试优化)、D(客户对接)。
现在问题来了:这 3000 元额外奖金,怎么分才公平?(如果只看 "最后谁参与了",可能会忽略 "没人帮忙时谁的作用更大";SHAP 值的核心就是 "考虑所有可能的分工组合,算每个人的平均贡献")
step1:计算每个人在不同组合中的 "边际贡献"
"边际贡献" 就是 "有没有这个人,项目结果的差距"------ 比如 "只有 A 和 B" vs "只有 A",差距就是 B 的贡献。
我们简化计算(只列关键组合):
- 组合 1:只有 A → 项目能拿 6000 元(比基准多 1000)→ A 的贡献 = 1000 元;
- 组合 2:只有 B → 项目能拿 6500 元(比基准多 1500)→ B 的贡献 = 1500 元;
- 组合 3:只有 C → 项目能拿 5500 元(比基准多 500)→ C 的贡献 = 500 元;
- 组合 4:只有 D → 项目能拿 5200 元(比基准多 200)→ D 的贡献 = 200 元;
- 组合 5:A+B → 项目能拿 7000 元(比基准多 2000)→ 此时 A 的贡献 = 2000-1500=500(没 A 时 B 能拿 1500,有 A 后多 500),B 的贡献 = 2000-1000=1000;
- 组合 6:A+B+C+D(全员)→ 项目能拿 8000 元(比基准多 3000)→ 每个人的贡献 = 总额外奖金 - 其他人单独组合的贡献(比如 A 的贡献 = 3000 - (B+C+D 的贡献)= 3000-2200=800)。
step2:计算每个人的 "平均边际贡献"(即 SHAP 值)
把每个人在所有组合中的边际贡献加起来,取平均值 ------ 这就是 "公平的功劳分配":
- A 的 SHAP 值:(1000 + 500 + 800 + ...)/ 所有组合数 ≈ 800 元;
- B 的 SHAP 值:(1500 + 1000 + 900 + ...)/ 所有组合数 ≈ 1200 元;
- C 的 SHAP 值:(500 + 600 + 700 + ...)/ 所有组合数 ≈ 700 元;
- D 的 SHAP 值:(200 + 300 + 300 + ...)/ 所有组合数 ≈ 300 元;
step3:验证公平性(SHAP 的核心性质:加和性)
800(A)+ 1200(B)+ 700(C)+ 300(D)= 3000 元(正好等于额外奖金总额);基准奖金 5000 + 3000(总 SHAP 值)= 8000 元(你们团队的实际奖金)------ 分毫不差!
对应到模型解释:
- 模型预测值 = 基准值(平均奖金 5000) + 所有特征的 SHAP 值(A+B+C+D 的功劳);
- 每个特征的 SHAP 值 = 这个特征对 "预测值偏离平均水平" 的 "公平贡献"(正贡献 = 加分,负贡献 = 减分);
- 比如 B 的 SHAP 值最高(1200),说明 "代码开发" 是让项目奖金超过平均水平的最关键因素 ------ 对应模型中 "B 特征对预测值的影响最大"。
场景 2:餐厅评分(更直观理解 "单个预测的解释")
如果觉得团队分红有点复杂,再看 "餐厅评分"------ 你给一家餐厅打了 8 分(满分 10 分),而所有餐厅的平均评分是 5 分,SHAP 值就是 "每个因素(口味、环境、服务、价格)让你多打了 3 分(8-5),各自贡献了多少"。
具体拆解:
- 基准分(平均评分):5 分;
- 你的评分(预测值):8 分;
- 总额外分数(总贡献):3 分;
- 影响因素(特征):口味、环境、服务、价格。
用 SHAP 值计算后,结果可能是:
- 口味的 SHAP 值:+1.5 分(好吃!是最大加分项);
- 环境的 SHAP 值:+1.0 分(装修干净,加分);
- 服务的 SHAP 值:+0.3 分(服务员态度还行,小加分);
- 价格的 SHAP 值:+0.2 分(性价比不错,微加分);
1.5+1.0+0.3+0.2=3 分(正好等于额外分数),5+3=8 分(你的最终评分)。
如果另一家餐厅你只打了 4 分(低于平均 5 分),SHAP 值可能是:
- 口味的 SHAP 值:-0.5 分(不好吃,减分);
- 环境的 SHAP 值:-0.3 分(有点脏,减分);
- 服务的 SHAP 值:+0.1 分(服务还行,小加分);
- 价格的 SHAP 值:-0.3 分(太贵,减分);
-0.5-0.3+0.1-0.3=-1 分(总贡献),5+(-1)=4 分(你的评分)------ 清晰说明 "为什么这家餐厅评分低":主要是口味不好和价格太贵。
一句话总结 SHAP 值:
SHAP 值就是给每个 "影响因素(特征)" 的 "功劳打分"------ 正分是 "加分项",负分是 "减分项",所有分数加起来,就是 "这个结果(预测值)和平均水平的差距"。它的核心是 "公平":不管因素之间怎么搭配,都能算出每个因素的真实贡献,不让某个因素 "被低估" 或 "被高估"。
比如模型预测 "某用户会购买商品"(预测值 = 80% 购买概率,平均概率 = 50%),SHAP 值就能告诉你:"年龄" 贡献了 + 10%,"消费金额" 贡献了 + 15%,"浏览时长" 贡献了 + 5%,加起来正好 30%------ 这就是 "为什么这个用户会买" 的答案!
对于零基础、理解能力稍弱的学习者来说,学习 numpy 数组时想要提升理解能力,核心是把抽象概念 "具象化"、把复杂操作 "拆解开"、用 "动手 + 复盘" 代替 "死记硬背"。分享几个具体、好落地的方法,你可以一步步跟着做:
一、用 "生活类比" 把抽象概念变具体
numpy 里的 "形状""维度""广播" 这些词很抽象,用生活里的东西类比,一下子就懂了:
- 一维数组 :像排队买奶茶的队伍,只有 "前后",比如
[1,2,3]就是 3 个人排成一队; - 二维数组 :像 Excel 表格,有 "行" 和 "列",比如
[[1,2],[3,4]]就是 2 行 2 列的表格; - 三维数组 :像一沓 Excel 表格,比如
[[[1,2],[3,4]],[[5,6],[7,8]]]就是 2 张 "2 行 2 列" 的表格叠在一起; - reshape(改形状):像把排队的人重新排成 "2 行 3 列" 的方阵 ------ 只要总人数不变,怎么排都行;
- 广播机制 :像给全班同学发作业本,不用一个一个递,直接 "广播" 发下去(比如数组
[1,2,3]加 2,就是给每个元素都 "发" 一个 2)。
二、"一行代码 + 运行结果",动手验证每一个知识点
不要只看教程,一定要自己敲代码、改参数、看结果 ------ 哪怕是教程里的例子,也要亲手敲一遍,再改改数值试试:比如学reshape时:
- 先敲
a = np.array([1,2,3,4,5,6]),运行看a.shape(输出(6,)); - 再敲
a.reshape(2,3),运行看结果(变成 2 行 3 列); - 故意试错:敲
a.reshape(2,4)(元素总数 6≠2×4),看报错信息(ValueError: cannot reshape array of size 6 into shape (2,4))------ 你就会记住 "reshape 必须保证元素总数匹配"。
再比如学 "按行 / 列求和" 时:
- 先建一个二维数组
b = np.array([[1,2],[3,4]]); - 敲
np.sum(b, axis=0),看结果[4,6](列求和); - 再敲
np.sum(b, axis=1),看结果[3,7](行求和); - 对比两次结果,你就懂了:
axis=0是 "竖着加",axis=1是 "横着加"。
三、把复杂操作 "拆成小步骤",逐个突破
遇到比如 "三维数组索引""矩阵乘法" 这种难的内容,别慌,拆成最小的步骤:比如学 "二维数组索引b[0,1]":
- 先想 "
b[0]是什么?"------ 运行看,是第一行[1,2]; - 再想 "
b[0][1]是什么?"------ 运行看,是第一行的第二个元素2; - 最后知道 "
b[0,1]和b[0][1]是一个意思,只是 numpy 的简写"。
再比如学 "矩阵乘法A@B":
- 先建简单的数组:
A = np.array([[1,2],[3,4]])(2 行 2 列),B = np.array([[5],[6]])(2 行 1 列); - 先算手动计算结果:第一行
1×5 + 2×6 = 17,第二行3×5 + 4×6 = 39; - 再运行
A@B,看结果是不是[[17],[39]]------ 手动算一遍,再对比代码结果,矩阵乘法的规则就懂了。
四、用 "小任务" 代替 "孤立记知识点"
学完单个知识点后,给自己出个 "小任务",把零散的知识点串起来用 ------ 用起来的知识才记得住:比如学完 "创建数组 + 索引 + 统计" 后,任务可以是:
- 生成一个 "3 行 4 列" 的随机整数数组(范围 1-10);
- 取出第二行的所有元素;
- 计算每列的平均值;
- 把数组里大于 5 的元素改成 0。
你会发现,为了完成任务,你需要回忆 "np.random.randint()怎么用""二维数组索引怎么写""np.mean()怎么指定 axis""条件索引怎么弄"------ 这个过程比单纯背知识点理解得深 10 倍。
五、记 "错题本" 和 "疑问本",把模糊点弄透
学习时遇到的报错、不懂的地方,一定要记下来,当天弄清楚:
- 错题本 :比如 "为什么
a + b报错?"(因为a是 (2,3),b是 (3,2),形状不兼容),记下来原因和解决方法; - 疑问本 :比如 "
np.dot()和@有区别吗?",查清楚后写下来:"二维数组时一样,高维数组有区别"。
每周翻一次,之前模糊的点会越来越清晰 ------ 理解能力就是在 "解决疑问" 的过程中慢慢提升的。
六、用 "可视化" 帮自己 "看到" 数组
如果对数值没感觉,可以用简单的可视化工具(比如matplotlib)把数组画出来:
- 一维数组画成折线图:
plt.plot([1,2,3,4]),能看到数值的变化; - 二维数组画成热力图:
plt.imshow([[1,2],[3,4]]),颜色深浅对应数值大小,一眼能看出 "哪里数值大"。
可视化能让你从 "看数字" 变成 "看规律",理解起来更轻松。
最后想说:别怕 "慢",理解比速度重要
你不用追求 "一天学完所有 numpy 操作",哪怕一天只搞懂 "reshape" 和 "axis=0/1",也是进步。numpy 的核心逻辑其实很简单:用 "数组" 代替 "列表",让数值运算更高效,围绕这个核心,慢慢拆解每个操作,你会发现越学越顺~