如何给Three.js中ExtrudeGeometry的不同面设置不同材质

前言

Three.js有很多基础的几何体，对于一些简单的图形形状，可以不用每次都劳烦建模的同学去提供一个模型，常常这些基础几何体就可以绘制了。ExtrudeGeometry是在开发中非常常用的一种几何体，它非常灵活，可以先用一系列二维顶点绘制一个二维图形，然后沿着一定的方向将这个二维图形拉成一个三维几何体，这在很多场景下非常有用，比如隧道、建筑大楼，都可以用这种方式生成一个简单的示意性的几何体。

但是，如果需要给这个几何体设置材质时，又会感觉不够灵活了，要么只能全部表面都用一直材质；要么就是两种材质：顶面底面一种，侧面一种。这在对于很多场景就不够用了，很多场景下，我们希望给不同的面使用不同的材质，甚至我们想自己设置顶点的uv属性。

其实从WebGL的角度来说，一个几何体的形状无非就是设置顶点，给几何体贴纹理无非就是传入一张纹理贴图然后给每个顶点设置正确的uv值。所以想实现灵活的给ExtrudeGeometry使用材质，还是要探究ExtrudeGeometry的顶点是如何生成的。这又来到了我们的传统艺能------阅读源码，这篇文章的就是通过阅读ExtrudeGeometry的源码，来探究ExtrudeGeometry的顶点是怎样生成的，然后我们可以将顶点设置不同的group，然后就可以为每一组设置不同的材质了。

这里还是要提一句，我们给场景中添加一个mesh时，一般要传入一个geometry和一个material,分别代表这个mesh的几何形态和外观材质，material通常是一个Material的子类对象，比如MeshLambertMaterial、MeshPhongMaterial、MeshPhysicalMaterial等。但也可以是一个数组，在这种情况下，这个数组的index就对应geometry的顶点的group，geometry上记录这所有group的起始顶点start、顶点数量count和材质索引materialIndex。所以只要我们能给ExtrudeGeometry对象中的的顶点设置group，我们可以任意给不同的面设置不同的材质。

ExtrudeGeometry绘制原理

1.绘制二维平面

首先绘制一个二维平面，我们这里就以官方示例为例，也就是最简单的矩形，长宽都是1。然后获取这个二维平面的二维顶点vertices，这里就是四边形的四个顶点(0,0),(0,1),(1,1),(1,0)，可以注意到，这里的顶点是顺时针排列的。如果是逆时针，还得将其转为顺时针。这里可以看到这个shape中间可能还会有空洞（holes），我们这篇文章就不考虑这种比较复杂的情况了（其实原理上也相差不大，就是要增加很多顶点和表面）。将vertices赋值给contour，如果有holes，要将holes的顶点写入vertices中，所以这里有一行注释，意思是contour是外圈的顶点，vetices还有holes的顶点。对于本文这种没有holes的实例，contour和vertices的值就是一模一样的。

const shapePoints = shape.extractPoints( curveSegments );

let vertices = shapePoints.shape;
const holes = shapePoints.holes;

const reverse = ! ShapeUtils.isClockWise( vertices );

if ( reverse ) {

        vertices = vertices.reverse();

        // Maybe we should also check if holes are in the opposite direction, just to be safe ...

        for ( let h = 0, hl = holes.length; h < hl; h ++ ) {

                const ahole = holes[ h ];

                if ( ShapeUtils.isClockWise( ahole ) ) {

                        holes[ h ] = ahole.reverse();

                }

        }

}
................
const contour = vertices; // vertices has all points but contour has only points of circumference
for ( let h = 0; h < numHoles; h ++ ) {

        const ahole = holes[ h ];

        vertices = vertices.concat( ahole );

}

2.求顶点向外扩的向量

ExtrudeGeometry是可以设置斜面倒角的，这里牵扯到三个参数，bevelEnabled、bevelThickness、bevelSize、bevelOffset、bevelSegments。这里bevelEnabled表示是否有斜面倒角，bevelSegments表示斜面倒角分为几段。 bevelThickness表示这个斜面倒角在纵线（z方向）上的长度。bevelSize和bevelOffset就得结合图来看了。bevelOffset表示shape还需要在其基础上向外扩大多少，bevelSize表示倒角顶面和底面的高度差。
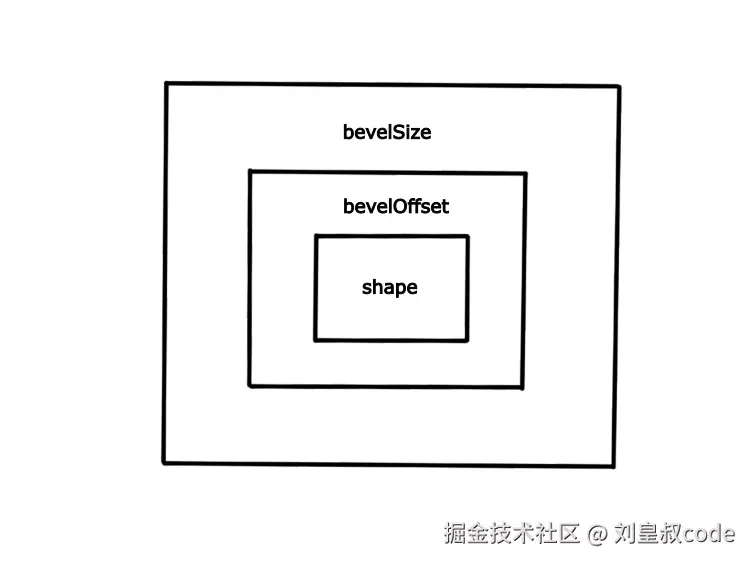要将shape的顶点外扩，也就是求每个顶点向外扩后得到的新顶点的坐标，那就要求每个顶点外扩的方向向量。这一节主要就是介绍如何求这个外扩向量。

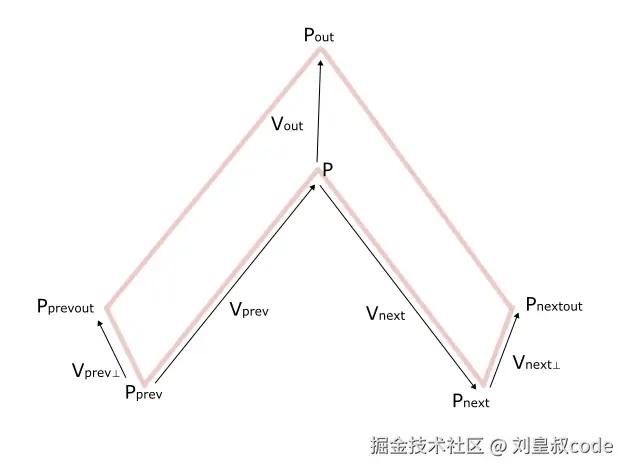
设某个顶点的坐标是 <math xmlns="http://www.w3.org/1998/Math/MathML"> P ( x v , y v ) P(x_v,y_v) </math>P(xv,yv)，这个点的前一个点为 <math xmlns="http://www.w3.org/1998/Math/MathML"> P p r e v ( x p r e v , y p r e v ) P_{prev}(x_{prev},y_{prev}) </math>Pprev(xprev,yprev)，后一个点为 <math xmlns="http://www.w3.org/1998/Math/MathML"> P n e x t ( x n e x t , y n e x t ) P_{next}(x_{next},y_{next}) </math>Pnext(xnext,ynext)。这三个点可以构成两个向量，分别是：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> V p r e v ( x v p r e v , y v p r e v ) = P − P p r e v V_{prev}(x_{vprev},y_{vprev})=P-P_{prev} </math>Vprev(xvprev,yvprev)=P−Pprev
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> V n e x t ( x v n e x t , y v n e x t ) = P n e x t − P V_{next}(x_{vnext},y_{vnext})=P_{next}-P </math>Vnext(xvnext,yvnext)=Pnext−P

与 <math xmlns="http://www.w3.org/1998/Math/MathML"> V p r e v V_{prev} </math>Vprev垂直，指向shape外的显然向量为 <math xmlns="http://www.w3.org/1998/Math/MathML"> V p r e v ⊥ ( − y v p r e v , x v p r e v ) V_{prev\bot}(-y_{vprev},x_{vprev}) </math>Vprev⊥(−yvprev,xvprev)；同理与 <math xmlns="http://www.w3.org/1998/Math/MathML"> V n e x t V_{next} </math>Vnext垂直，指向shape外的向量为 <math xmlns="http://www.w3.org/1998/Math/MathML"> V n e x t ⊥ ( − y v n e x t , x v n e x t ) V_{next\bot}(-y_{vnext},x_{vnext}) </math>Vnext⊥(−yvnext,xvnext)。 将 <math xmlns="http://www.w3.org/1998/Math/MathML"> V p r e v V_{prev} </math>Vprev垂直边向外扩1个单位，得到一个点：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P p r e v o u t ( x p r e v o u t , y p r e v o u t ) = P p r e v + V p r e v ⊥ ∣ V p r e v ⊥ ∣ P_{prevout}(x_{prevout},y_{prevout})=P_{prev}+\frac{V_{prev\bot}}{|V_{prev\bot}|} </math>Pprevout(xprevout,yprevout)=Pprev+∣Vprev⊥∣Vprev⊥

同理，将 <math xmlns="http://www.w3.org/1998/Math/MathML"> V n e x t V_{next} </math>Vnext垂直边向外扩1个单位，得到一个点：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P n e x t o u t ( x n e x t o u t , y n e x t o u t ) = P n e x t + V n e x t ⊥ ∣ V n e x t ⊥ ∣ P_{nextout}(x_{nextout},y_{nextout})=P_{next}+\frac{V_{next\bot}}{|V_{next\bot}|} </math>Pnextout(xnextout,ynextout)=Pnext+∣Vnext⊥∣Vnext⊥

然后以 <math xmlns="http://www.w3.org/1998/Math/MathML"> P p r e v o u t P_{prevout} </math>Pprevout为起点，以 <math xmlns="http://www.w3.org/1998/Math/MathML"> V p r e v V_{prev} </math>Vprev为方向画一条直线,表达式为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P = P p r e v o u t + t V p r e v P=P_{prevout}+tV_{prev} </math>P=Pprevout+tVprev

同理，以 <math xmlns="http://www.w3.org/1998/Math/MathML"> P n e x t o u t P_{nextout} </math>Pnextout为起点，以 <math xmlns="http://www.w3.org/1998/Math/MathML"> V n e x t V_{next} </math>Vnext为方向也可以画一条直线,表达式为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P = P n e x t o u t + s V n e x t P=P_{nextout}+sV_{next} </math>P=Pnextout+sVnext

这两条直线的交点就是P点向外扩后的点（特殊的三点共线的情况就先不考虑了），解方程：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P p r e v o u t + t V p r e v = P n e x t o u t + s V n e x t P_{prevout}+tV_{prev}=P_{nextout}+sV_{next} </math>Pprevout+tVprev=Pnextout+sVnext

就可以将交点位置的t和s都解出来。解方程的过程这里就省略了，感兴趣的可以手动解一下，最终：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> t i = ( x n e x t o u t − x p r e v o u t ) y v n e x t − ( y n e x t o u t − y p r e v o u t ) x v n e x t x v p r e v y v n e x t − y v p r e v x v n e x t t_i=\frac{(x_{nextout}-x_{prevout})y_{vnext}-(y_{nextout}-y_{prevout})x_{vnext}}{x_{vprev}y_{vnext}-y_{vprev}x_{vnext}} </math>ti=xvprevyvnext−yvprevxvnext(xnextout−xprevout)yvnext−(ynextout−yprevout)xvnext

顶点 <math xmlns="http://www.w3.org/1998/Math/MathML"> P P </math>P向外扩后的点为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P o u t = P p r e v o u t + t i V p r e v P_{out}=P_{prevout}+t_iV_{prev} </math>Pout=Pprevout+tiVprev

外扩向量为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> V o u t = P o u t − P V_{out}=P_{out}-P </math>Vout=Pout−P

如图所示：

这里注意一下，这个外扩的向量不是单位向量，所以也不用做归一化，除非原来的两个向量的夹角非常尖锐，需要做一定的缩短处理,可以看源码。

在ExtrudeGeometry的源码中，上文的过程被写为一个函数getBevelVec，这个函数就是专门用来求每个点的外扩向量的。代码基本上和我上文介绍的一致。要注意就两点：一是对三点共线做了判断；二是如果外扩的向量模大于2，就将它的长度归一化到2。

将每个点的外扩向量写入到oneHoleMovements和verticesMovements这两个数组中。（和上节一样，本文中的示例没有holes,所以这两个是一模一样的。）

function getBevelVec( inPt, inPrev, inNext ) {

        // computes for inPt the corresponding point inPt' on a new contour
        //   shifted by 1 unit (length of normalized vector) to the left
        // if we walk along contour clockwise, this new contour is outside the old one
        //
        // inPt' is the intersection of the two lines parallel to the two
        //  adjacent edges of inPt at a distance of 1 unit on the left side.

        let v_trans_x, v_trans_y, shrink_by; // resulting translation vector for inPt

        // good reading for geometry algorithms (here: line-line intersection)
        // http://geomalgorithms.com/a05-_intersect-1.html

        const v_prev_x = inPt.x - inPrev.x,
                v_prev_y = inPt.y - inPrev.y;
        const v_next_x = inNext.x - inPt.x,
                v_next_y = inNext.y - inPt.y;

        const v_prev_lensq = ( v_prev_x * v_prev_x + v_prev_y * v_prev_y );

        // check for collinear edges
        const collinear0 = ( v_prev_x * v_next_y - v_prev_y * v_next_x );
        //判断三点是否贡献
        if ( Math.abs( collinear0 ) > Number.EPSILON ) {

                // not collinear

                // length of vectors for normalizing

                const v_prev_len = Math.sqrt( v_prev_lensq );
                const v_next_len = Math.sqrt( v_next_x * v_next_x + v_next_y * v_next_y );

                // shift adjacent points by unit vectors to the left

                const ptPrevShift_x = ( inPrev.x - v_prev_y / v_prev_len );
                const ptPrevShift_y = ( inPrev.y + v_prev_x / v_prev_len );

                const ptNextShift_x = ( inNext.x - v_next_y / v_next_len );
                const ptNextShift_y = ( inNext.y + v_next_x / v_next_len );

                // scaling factor for v_prev to intersection point

                const sf = ( ( ptNextShift_x - ptPrevShift_x ) * v_next_y -
                                ( ptNextShift_y - ptPrevShift_y ) * v_next_x ) /
                        ( v_prev_x * v_next_y - v_prev_y * v_next_x );

                // vector from inPt to intersection point

                v_trans_x = ( ptPrevShift_x + v_prev_x * sf - inPt.x );
                v_trans_y = ( ptPrevShift_y + v_prev_y * sf - inPt.y );

                // Don't normalize!, otherwise sharp corners become ugly
                //  but prevent crazy spikes
                const v_trans_lensq = ( v_trans_x * v_trans_x + v_trans_y * v_trans_y );
                // 如果外扩向量的模大于2，就将它归一化到2，避免太尖锐的夹角。
                if ( v_trans_lensq <= 2 ) {

                        return new Vector2( v_trans_x, v_trans_y );

                } else {

                        shrink_by = Math.sqrt( v_trans_lensq / 2 );

                }

        } else {

                // handle special case of collinear edges

                let direction_eq = false; // assumes: opposite

                if ( v_prev_x > Number.EPSILON ) {

                        if ( v_next_x > Number.EPSILON ) {

                                direction_eq = true;

                        }

                } else {

                        if ( v_prev_x < - Number.EPSILON ) {

                                if ( v_next_x < - Number.EPSILON ) {

                                        direction_eq = true;

                                }

                        } else {

                                if ( Math.sign( v_prev_y ) === Math.sign( v_next_y ) ) {

                                        direction_eq = true;

                                }

                        }

                }

                if ( direction_eq ) {

                        // console.log("Warning: lines are a straight sequence");
                        v_trans_x = - v_prev_y;
                        v_trans_y = v_prev_x;
                        shrink_by = Math.sqrt( v_prev_lensq );

                } else {

                        // console.log("Warning: lines are a straight spike");
                        v_trans_x = v_prev_x;
                        v_trans_y = v_prev_y;
                        shrink_by = Math.sqrt( v_prev_lensq / 2 );

                }

        }

        return new Vector2( v_trans_x / shrink_by, v_trans_y / shrink_by );

}


const contourMovements = [];

for ( let i = 0, il = contour.length, j = il - 1, k = i + 1; i < il; i ++, j ++, k ++ ) {

        if ( j === il ) j = 0;
        if ( k === il ) k = 0;

        //  (j)---(i)---(k)
        console.log('i,j,k', contour[ i ], contour[ j ], contour[ k ])

        contourMovements[ i ] = getBevelVec( contour[ i ], contour[ j ], contour[ k ] );

}

const holesMovements = [];
let oneHoleMovements, verticesMovements = contourMovements.concat();

for ( let h = 0, hl = numHoles; h < hl; h ++ ) {

        const ahole = holes[ h ];

        oneHoleMovements = [];

        for ( let i = 0, il = ahole.length, j = il - 1, k = i + 1; i < il; i ++, j ++, k ++ ) {

                if ( j === il ) j = 0;
                if ( k === il ) k = 0;

                //  (j)---(i)---(k)
                oneHoleMovements[ i ] = getBevelVec( ahole[ i ], ahole[ j ], ahole[ k ] );

        }

        holesMovements.push( oneHoleMovements );
        verticesMovements = verticesMovements.concat( oneHoleMovements );

}

3.生成顶点

之前我们所介绍的都是生成二维顶点，接下来就是生成三维顶点了。三维顶点就是二维顶点作为x和y，再增加一个z方向上的值就行了。所以三维顶点的生成就是给原来的二维顶点增加z值。具体的顺序是沿着拉长的方向从z值依次增大。具体z值是多少，是和bevelSegments、bevelThickness、steps、depth这些参数有关，分别代表倒角斜面的分段和在z方向上的长度，主体的分段和在z方向上的长度。

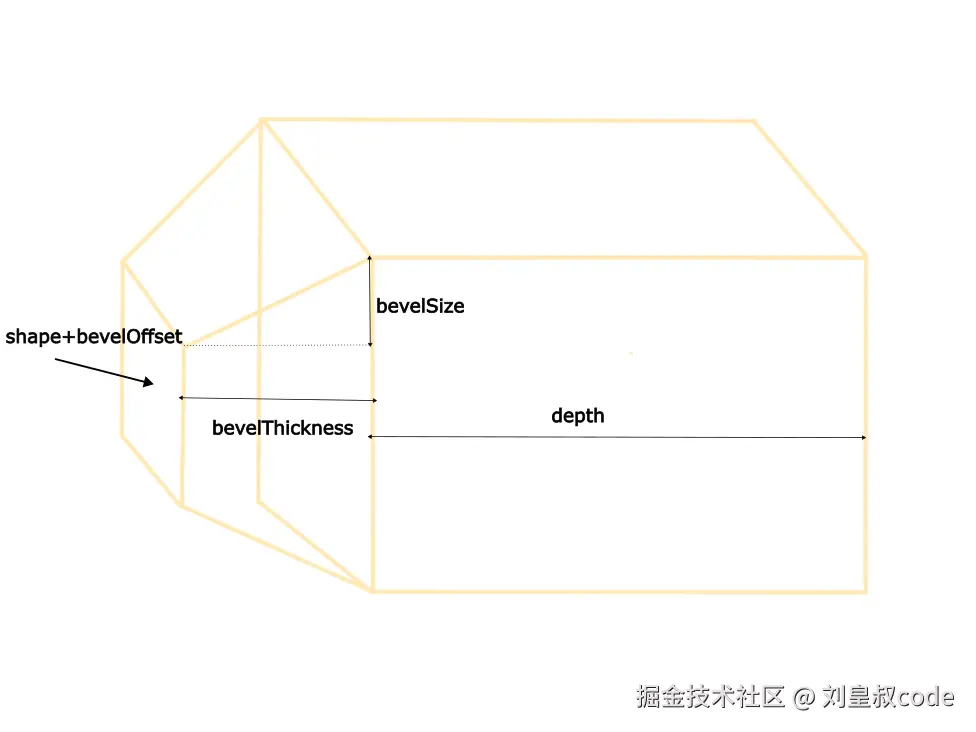先生成底面的倒角斜面，可以看到，根据bevelSegments的大小，有几个bevelSegments就分为几段，每一段都是contour.length个顶点。每一段中，会计算一个z值和bs值，底面倒角的z值是负值，bs值是contour中顶点在xy平面上向外扩时，加上节求的外扩向量时，向量乘的系数。可以看到，底面的系数为0，就是一点都不外扩，后面越扩越大，形成一个斜面。scalePt2函数的功能是给一个二维顶点加上一个向量乘系数，正好用作计算外扩的顶点坐标。这里注意生成了一个faces数组，这个数组存着顶面和底面每个三角面的顶点索引，下一节会用到。

let faces;

if ( bevelSegments === 0 ) {

        faces = ShapeUtils.triangulateShape( contour, holes );

} else {

        const contractedContourVertices = [];
        const expandedHoleVertices = [];

        // Loop bevelSegments, 1 for the front, 1 for the back

        for ( let b = 0; b < bevelSegments; b ++ ) {

                //for ( b = bevelSegments; b > 0; b -- ) {

                const t = b / bevelSegments;
                const z = bevelThickness * Math.cos( t * Math.PI / 2 );
                const bs = bevelSize * Math.sin( t * Math.PI / 2 ) + bevelOffset;

                // contract shape

                for ( let i = 0, il = contour.length; i < il; i ++ ) {

                        const vert = scalePt2( contour[ i ], contourMovements[ i ], bs );

                        v( vert.x, vert.y, - z );
                        if ( t === 0 ) contractedContourVertices.push( vert );

                }

                // expand holes

                for ( let h = 0, hl = numHoles; h < hl; h ++ ) {

                        const ahole = holes[ h ];
                        oneHoleMovements = holesMovements[ h ];
                        const oneHoleVertices = [];
                        for ( let i = 0, il = ahole.length; i < il; i ++ ) {

                                const vert = scalePt2( ahole[ i ], oneHoleMovements[ i ], bs );

                                v( vert.x, vert.y, - z );
                                if ( t === 0 ) oneHoleVertices.push( vert );

                        }

                        if ( t === 0 ) expandedHoleVertices.push( oneHoleVertices );

                }

        }

        faces = ShapeUtils.triangulateShape( contractedContourVertices, expandedHoleVertices );

}

const flen = faces.length;

接下来生成主体部分，主体部分的bs值为bevelSize加bevelOffset。第一段的z值为0，接下来每一段的z值与段号s和长度depth有关，为 <math xmlns="http://www.w3.org/1998/Math/MathML"> d e p t h / s t e p s × s depth/steps×s </math>depth/steps×s。

const bs = bevelSize + bevelOffset;

// Back facing vertices

for ( let i = 0; i < vlen; i ++ ) {

        const vert = bevelEnabled ? scalePt2( vertices[ i ], verticesMovements[ i ], bs ) : vertices[ i ];

        if ( ! extrudeByPath ) {

                v( vert.x, vert.y, 0 );

        } else {

                // v( vert.x, vert.y + extrudePts[ 0 ].y, extrudePts[ 0 ].x );

                normal.copy( splineTube.normals[ 0 ] ).multiplyScalar( vert.x );
                binormal.copy( splineTube.binormals[ 0 ] ).multiplyScalar( vert.y );

                position2.copy( extrudePts[ 0 ] ).add( normal ).add( binormal );

                v( position2.x, position2.y, position2.z );

        }

}

// Add stepped vertices...
// Including front facing vertices

for ( let s = 1; s <= steps; s ++ ) {

        for ( let i = 0; i < vlen; i ++ ) {

                const vert = bevelEnabled ? scalePt2( vertices[ i ], verticesMovements[ i ], bs ) : vertices[ i ];

                if ( ! extrudeByPath ) {

                        v( vert.x, vert.y, depth / steps * s );

                } else {

                        // v( vert.x, vert.y + extrudePts[ s - 1 ].y, extrudePts[ s - 1 ].x );

                        normal.copy( splineTube.normals[ s ] ).multiplyScalar( vert.x );
                        binormal.copy( splineTube.binormals[ s ] ).multiplyScalar( vert.y );

                        position2.copy( extrudePts[ s ] ).add( normal ).add( binormal );

                        v( position2.x, position2.y, position2.z );

                }

        }

}

最后是顶面倒角斜面，和底面类似，不过多介绍了。

for ( let b = bevelSegments - 1; b >= 0; b -- ) {

        const t = b / bevelSegments;
        const z = bevelThickness * Math.cos( t * Math.PI / 2 );
        const bs = bevelSize * Math.sin( t * Math.PI / 2 ) + bevelOffset;

        // contract shape

        for ( let i = 0, il = contour.length; i < il; i ++ ) {

                const vert = scalePt2( contour[ i ], contourMovements[ i ], bs );
                v( vert.x, vert.y, depth + z );

        }

        // expand holes

        for ( let h = 0, hl = holes.length; h < hl; h ++ ) {

                const ahole = holes[ h ];
                oneHoleMovements = holesMovements[ h ];

                for ( let i = 0, il = ahole.length; i < il; i ++ ) {

                        const vert = scalePt2( ahole[ i ], oneHoleMovements[ i ], bs );

                        if ( ! extrudeByPath ) {

                                v( vert.x, vert.y, depth + z );

                        } else {

                                v( vert.x, vert.y + extrudePts[ steps - 1 ].y, extrudePts[ steps - 1 ].x + z );

                        }

                }

        }

}

生成的顶点的x,y,z值依次由v函数加入到placeholder数组中：

function v( x, y, z ) {

        placeholder.push( x );
        placeholder.push( y );
        placeholder.push( z );

}

生成三角面

有了顶点，下来就是根据顶点生成三角面了，这里的所说的三角面，其实就对应的顶点着色器中vec3类型的position属性。一个三角面有三个顶点，每个顶点是一个三维坐标。

所以，一个三角面可以用三个顶点索引来表示，顶点索引乘3就可以找到顶点坐标值的索引，坐标值的索引+0，+1，+2分别就对应顶点x，y，z的坐标值，可以用这三个索引去placeholder中查询。

先生成顶面和底面，上文中生成的faces正好派上用场，这里底面的顶点索引就是face中的值，顶面的顶点由于在队尾，需要加上偏移量。f3函数就是通过三个顶点索引将顶点数据加入到verticesArray数组中，这个数组最终要传给顶点着色器的position属性的。

function buildLidFaces() {

        const start = verticesArray.length / 3;

        if ( bevelEnabled ) {

                let layer = 0; // steps + 1
                let offset = vlen * layer;

                // Bottom faces

                for ( let i = 0; i < flen; i ++ ) {

                        const face = faces[ i ];
                        f3( face[ 2 ] + offset, face[ 1 ] + offset, face[ 0 ] + offset );

                }

                layer = steps + bevelSegments * 2;
                offset = vlen * layer;

                // Top faces

                for ( let i = 0; i < flen; i ++ ) {

                        const face = faces[ i ];
                        f3( face[ 0 ] + offset, face[ 1 ] + offset, face[ 2 ] + offset );

                }

        } else {

                // Bottom faces

                for ( let i = 0; i < flen; i ++ ) {

                        const face = faces[ i ];
                        f3( face[ 2 ], face[ 1 ], face[ 0 ] );

                }

                // Top faces

                for ( let i = 0; i < flen; i ++ ) {

                        const face = faces[ i ];
                        f3( face[ 0 ] + vlen * steps, face[ 1 ] + vlen * steps, face[ 2 ] + vlen * steps );

                }

        }

        scope.addGroup( start, verticesArray.length / 3 - start, 0 );

}

再生成四个侧面，四个侧面依次生成，每个侧面都根据分段生成一系列四边形，每个四边形由两个三角形组成。具体的四边形的四个顶点为： <math xmlns="http://www.w3.org/1998/Math/MathML"> V i s V_{is} </math>Vis， <math xmlns="http://www.w3.org/1998/Math/MathML"> V i + 1 s V_{i+1s} </math>Vi+1s， <math xmlns="http://www.w3.org/1998/Math/MathML"> V i s + 1 V_{is+1} </math>Vis+1， <math xmlns="http://www.w3.org/1998/Math/MathML"> V i + 1 s + 1 V_{i+1s+1} </math>Vi+1s+1，i代表侧面的棱号，i+1代表下一条棱，s代表段号，s+1代表下一段。f4函数就是通过四个顶点索引将两个三角面的顶点数据加入到verticesArray数组中。

function buildSideFaces() {

        const start = verticesArray.length / 3;
        let layeroffset = 0;
        sidewalls( contour, layeroffset );
        layeroffset += contour.length;

        for ( let h = 0, hl = holes.length; h < hl; h ++ ) {

                const ahole = holes[ h ];
                sidewalls( ahole, layeroffset );

                //, true
                layeroffset += ahole.length;

        }


        scope.addGroup( start, verticesArray.length / 3 - start, 1 );


}

function sidewalls( contour, layeroffset ) {

        let i = contour.length;

        while ( -- i >= 0 ) {

                const j = i;
                let k = i - 1;
                if ( k < 0 ) k = contour.length - 1;

                //console.log('b', i,j, i-1, k,vertices.length);

                for ( let s = 0, sl = ( steps + bevelSegments * 2 ); s < sl; s ++ ) {

                        const slen1 = vlen * s;
                        const slen2 = vlen * ( s + 1 );

                        const a = layeroffset + j + slen1,
                                b = layeroffset + k + slen1,
                                c = layeroffset + k + slen2,
                                d = layeroffset + j + slen2;

                        f4( a, b, c, d );

                }

        }

}

这里注意，在生成上下底面和生成侧面后各调用了一下addGroup，这就是给这两部分分别设置group，这也就是为什么在Mesh的Material属性为数组时，数组中的两种Material对象分别设置给顶底面和侧面。

给不同面设置不同材质

生成顶点和三角面介绍完了，可以看到，ExtrudeGeometry中只设置了两个group，一种是顶底面，一种是侧面。那么其实给每个面都设置一个group值，就可以给每个面设置不同的材质了。这个只需要将源码略作修改就能做到。将原来的buildLidFaces函数拆成两个函数buildBottomFaces和buildTopFaces，分别生成底面和顶面，然后分别设置group的索引为0和1。

function buildBottomFaces() {

        const start = verticesArray.length / 3;

        if (bevelEnabled) {

                let layer = 0; // steps + 1
                let offset = vlen * layer;

                // Bottom faces

                for (let i = 0; i < flen; i++) {

                        const face = faces[i];
                        f3(face[2] + offset, face[1] + offset, face[0] + offset);

                }

        } else {

                // Bottom faces

                for (let i = 0; i < flen; i++) {

                        const face = faces[i];
                        f3(face[2], face[1], face[0]);

                }

        }

        scope.addGroup(start, verticesArray.length / 3 - start, 0);

}

function buildTopFaces() {

        const start = verticesArray.length / 3;

        if (bevelEnabled) {
                let layer = steps + bevelSegments * 2;
                let offset = vlen * layer;

                // Top faces

                for (let i = 0; i < flen; i++) {

                        const face = faces[i];
                        f3(face[0] + offset, face[1] + offset, face[2] + offset);

                }

        } else {

                // Top faces

                for (let i = 0; i < flen; i++) {

                        const face = faces[i];
                        f3(face[0] + vlen * steps, face[1] + vlen * steps, face[2] + vlen * steps);

                }

        }

        scope.addGroup(start, verticesArray.length / 3 - start, 1);

}

生成侧面时，修改buildSideFaces和sidewalls每个侧面都设置一次group。

function buildSideFaces() {

        // const start = verticesArray.length / 3;
        let layeroffset = 0;
        sidewalls(contour, layeroffset);
        layeroffset += contour.length;

        for (let h = 0, hl = holes.length; h < hl; h++) {

                const ahole = holes[h];
                sidewalls(ahole, layeroffset);

                //, true
                layeroffset += ahole.length;

        }


        // scope.addGroup(start, verticesArray.length / 3 - start, 2);


}

function sidewalls(contour, layeroffset) {

        let i = contour.length;
        let group = 2
        while (--i >= 0) {
                const start = verticesArray.length / 3;
                const j = i;
                let k = i - 1;
                if (k < 0) k = contour.length - 1;

                //console.log('b', i,j, i-1, k,vertices.length);

                for (let s = 0, sl = (steps + bevelSegments * 2); s < sl; s++) {

                        const slen1 = vlen * s;
                        const slen2 = vlen * (s + 1);

                        const a = layeroffset + j + slen1,
                                b = layeroffset + k + slen1,
                                c = layeroffset + k + slen2,
                                d = layeroffset + j + slen2;

                        f4(a, b, c, d);

                }
                //每个侧面都设置一个group值
                scope.addGroup(start, verticesArray.length / 3 - start, group);
                group++;
        }

}

对比

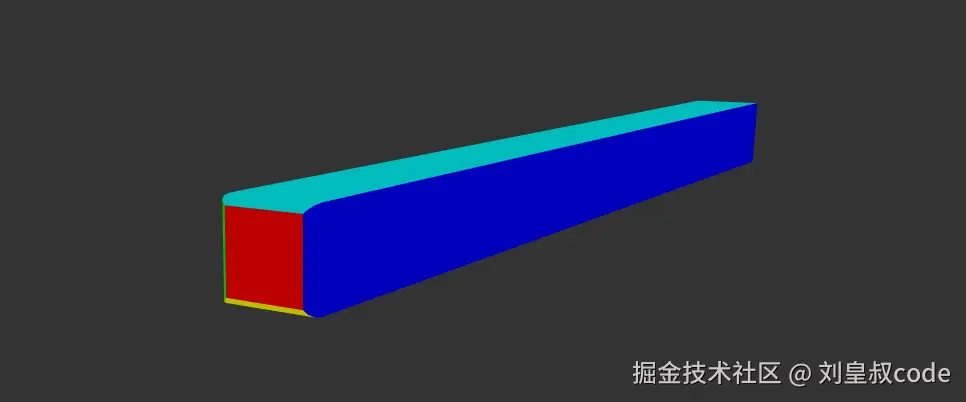
绘制了一个底面为正方形的ExtrudeGeometry，Material设置了一个数组，这个数组中包含六种不同颜色的material,未改源码之前只显示前两种，分别设置给顶底面和四个侧面。修改后六个面就设置成六个不同的material。

import { useEffect, useRef } from "react"
import * as THREE from './threeSource/Three.js';
import { OrbitControls } from 'three/addons/controls/OrbitControls.js';
import { RGBELoader } from 'three/addons/loaders/RGBELoader.js';
let camera
let scene
let renderer
let controls
let requestId

function ThreeContainer() {
  const threeContainer = useRef(null);

  useEffect(() => {
    if (threeContainer.current) {
      scene = new THREE.Scene();
      scene.background = new THREE.Color(0x333333);
      scene.environment = new RGBELoader().load('/venice_sunset_1k.hdr');
      scene.environment.mapping = THREE.EquirectangularReflectionMapping;
      camera = new THREE.PerspectiveCamera(40, window.innerWidth / window.innerHeight, 0.1, 100);
      camera.position.set(4.25, 1.4, - 4.5);
      renderer = new THREE.WebGLRenderer({ antialias: true });
      renderer.toneMapping = THREE.ReinhardToneMapping;
      renderer.setSize(threeContainer.current.clientWidth, threeContainer.current.clientHeight);
      renderer.setPixelRatio(window.devicePixelRatio);

      controls = new OrbitControls(camera, renderer.domElement);
      threeContainer.current.appendChild(renderer.domElement);
      const length = 1, width = 1;

      const shape = new THREE.Shape();
      shape.moveTo(0, 0);
      shape.lineTo(0, width);
      shape.lineTo(length, width);
      shape.lineTo(length, 0);
      shape.lineTo(0, 0);

      const extrudeSettings = {
        steps: 2,
        depth: 4,
        bevelEnabled: true,
      };

      const geometry = new THREE.ExtrudeGeometry(shape, extrudeSettings);
      const material1 = new THREE.MeshBasicMaterial({ color: 0xFF0000,  });
      const material2 = new THREE.MeshBasicMaterial({ color: 0xFFA500,  });
      const material3 = new THREE.MeshBasicMaterial({ color: 0xFFFF00, });
      const material4 = new THREE.MeshBasicMaterial({ color: 0x00FF00, });
      const material5 = new THREE.MeshBasicMaterial({ color: 0x00FFFF, });
      const material6 = new THREE.MeshBasicMaterial({ color: 0x0000FF, });
      const mesh = new THREE.Mesh(geometry, [material1, material2, material3, material4, material5, material6]);
      scene.add(mesh);

      requestId = requestAnimationFrame(animate);
    }
    return () => {
      destroyRenderer()
    };
  }, [])

  function destroyRenderer() {
    if (requestId) {
      window.cancelAnimationFrame(requestId)
    }
    if (scene) {
      scene.traverse(obj => {
        if (obj instanceof THREE.Mesh) {
          if (obj.isMesh) {
            obj.geometry?.dispose();
            if (Array.isArray(obj.material)) {
              obj.material.forEach(m => disposeMaterial(m));
            } else {
              disposeMaterial(obj.material);
            }
          }
        }
      });
    }

    if (renderer) {
      renderer.domElement.remove();
      renderer.dispose();
      renderer.forceContextLoss();
      renderer = null
    }
  }
  function disposeMaterial(material) {
    material.dispose();
    Object.keys(material).forEach(key => {
      const val = material[key];
      if (val && val instanceof THREE.Texture) {
        // 类型断言后安全调用 dispose 方法
        val.dispose();
      }
    });
  }
  function animate() {
    // renderer?.clear()
    renderer?.render(scene, camera);
    if (controls) {
      controls.update()
    }
    requestAnimationFrame(animate);
  }

  return (
    <div ref={threeContainer} className="w-[100%] h-[100%]" id="three-container"></div>
  )
}

export default ThreeContainer

修改前：

修改后：