146. LRU缓存 - 技术栈

一种数据结构（哈希表+双向链表）

实现方式一：

使用语言自带的、封装好的数据结构。在python中这种数据结构为collections包中的OrderedDict。
其中move_to_end(key)函数，是将该key移到链表的最后。
popitem() 是 collections.OrderedDict 的方法，用于移除并返回一个键值对，其中``last=False 参数指定移除最先插入的项（最旧的）。

Code

python 复制代码

class LRUCache(collections.OrderedDict):      ### 使用语言自带的、封装好的数据结构（哈希表+双向链表）

    def __init__(self, capacity: int):
        self.capacity = capacity
        

    def get(self, key: int) -> int:

        if key not in self:
            return -1
        
        self.move_to_end(key)
        return self[key]

        
    def put(self, key: int, value: int) -> None:

        if key in self:
            self.move_to_end(key)
        
        self[key] = value
        if len(self) > self.capacity:
            self.popitem(last=False)        ## popitem 用于移除并返回一个键值对, last=False 参数指定移除最先插入的项（最旧的）


# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

实现方式二：

自己手动创建一个哈希表+双向链表的数据结构。

Code

python 复制代码

class DLinkedNode:     ### 哈希表+双向链表的数据结构定义(这里只是其中的一个点)
    def __init__(self, key=0, value=0):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None


class LRUCache:

    def __init__(self, capacity: int):
        self.cache = dict()             ### 哈希表，用于快速判断是否存在, 存储这个key对应的node
        self.head = DLinkedNode()       ### 双向链表，用于定位存储的位置并进行修改
        self.tail = DLinkedNode()       ### head和tail都是dummy_node
        self.head.next = self.tail
        self.tail.prev = self.head
        self.capacity = capacity
        self.size = 0      

    def get(self, key: int) -> int:
        if key not in self.cache:
            return -1
        
        node = self.cache[key]      ### 
        self.move_to_head(node)
        return node.value
        

    def put(self, key: int, value: int) -> None:
        
        if key in self.cache:
            node = self.cache[key]
            self.move_to_head(node)
            node.value = value
        else:
            node = DLinkedNode(key=key,value=value)
            self.cache[key] = node
            self.add_to_head(node)          ## 添加到头部
            self.size += 1
            if self.size > self.capacity:
                remove = self.remove_tail()
                self.cache.pop(remove.key)
                self.size -= 1
    
    def move_to_head(self, node):
        self.remove_node(node)
        self.add_to_head(node)

    def add_to_head(self, node):
        node.prev = self.head
        node.next = self.head.next
        self.head.next.prev = node
        self.head.next = node

    def remove_tail(self):
        node = self.tail.prev
        self.remove_node(node)
        return node

    def remove_node(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev

    
# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

图解

数据结构初始化

head和tail是两个dummy_node，添加的节点位于这两个中间，其中越靠近head，越是最新添加进来的；相反，越靠近tail，则在缓存中待留的时间越久。双向链表中的每一个节点都是一个node，node下存储的是一个字典，我们可以通过存key，然后value是该key在双向链表中的node，这样的话就可以根据key快速定位到其在双向链表中的位置。

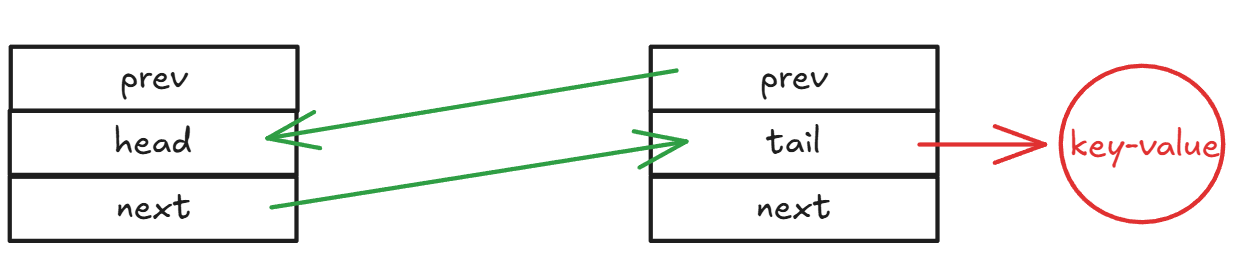
get()，查询函数

首先判断要get的key是否添加过，如果添加过的话，则根据key的值定位到node的位置，然后输出node下的value值，随后需要将该node移动到head处。

put()，添加函数

首先判断要添加的key是否添加过，如果添加过，则根据key的值定位到node的位置，然后修改node下的value值，随后需要将该node移动到head处。
如果没有添加过，那么需要新创建一个node，来存储key和value，随后需要在一个字典下存储这个key和node，以方便后续根据key直接在双向链表中找到node的位置。
如果添加后发现超出capacity，那需要移除最接近tail的尾部node。

add_to_head()，添加到头部函数

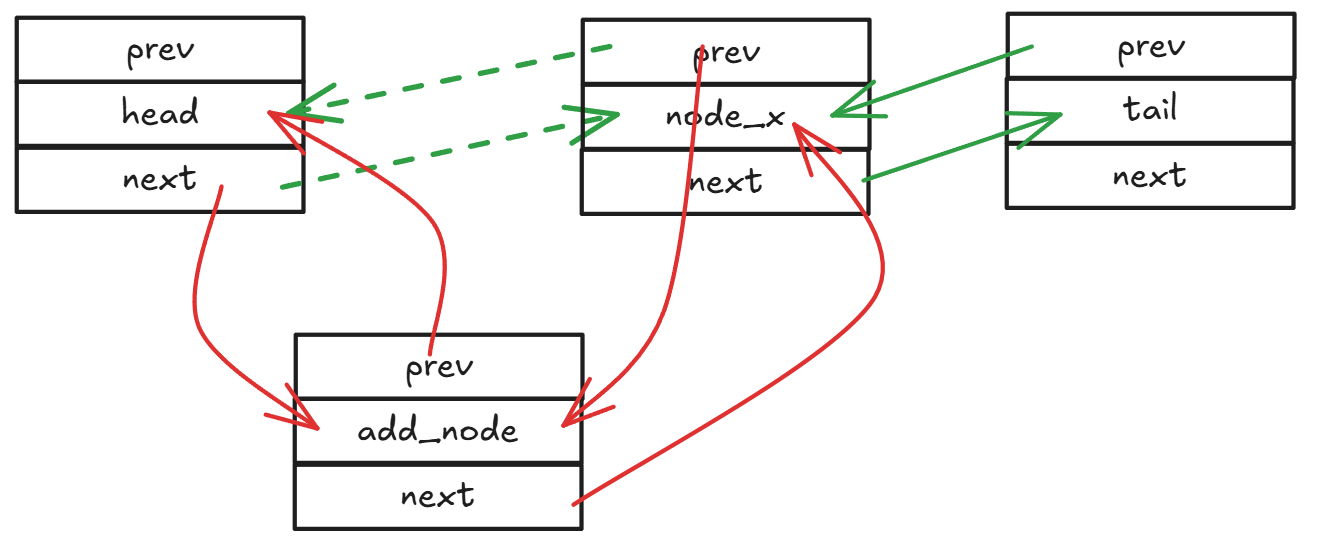
需要修改head、靠近head的节点、添加节点的prev和next指针，从而将节点添加到头部。

remove_node()，删除节点函数。

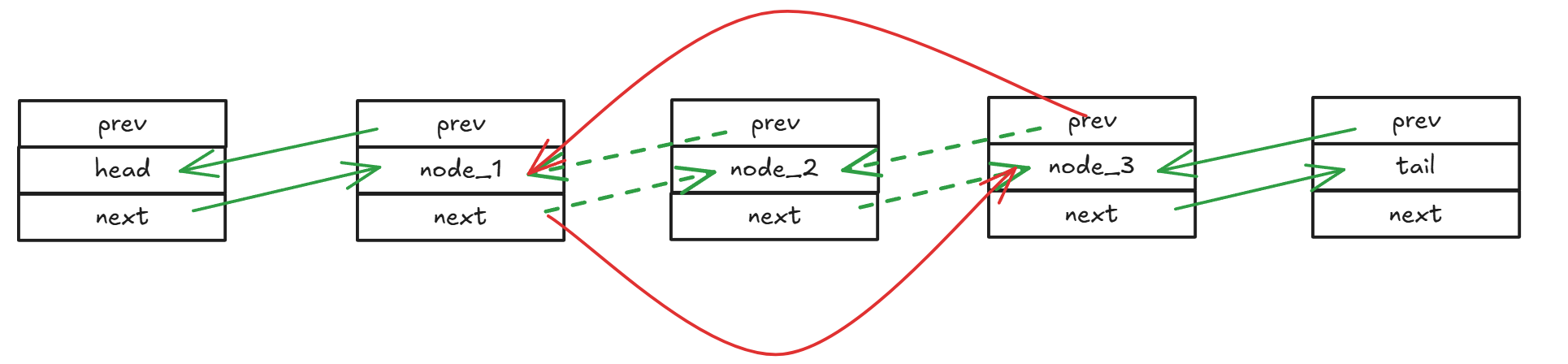
首先需要找到要删除节点的上一个节点和下一个节点，然后修改指针。

move_to_head()，移动到头部函数。

那实际上可以通过先把这个节点删除remove_node()，然后再将这个节点添加到头部add_to_head()。

remove_tail()，移动尾部的节点函数。

直接找到tail的上一个节点，然后用remove_node()直接对该节点进行删除。