大数据-106 Spark Graph X案例：1图计算、2连通图算法、3寻找相同用户高效分区、负载均衡与迭代优化

点一下关注吧！！！非常感谢！！持续更新！！！

🚀 AI篇持续更新中！（长期更新）

AI炼丹日志-31- 千呼万唤始出来 GPT-5 发布！"快的模型 + 深度思考模型 + 实时路由"，持续打造实用AI工具指南！📐🤖

💻 Java篇正式开启！（300篇）

目前2025年09月22日更新到： Java-130 深入浅出 MySQL MyCat 深入解析核心配置文件 server.xml 使用与优化 MyBatis 已完结，Spring 已完结，Nginx已完结，Tomcat已完结，分布式服务正在更新！深入浅出助你打牢基础！

📊 大数据板块已完成多项干货更新（300篇）：

包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！ 大数据-278 Spark MLib - 基础介绍机器学习算法梯度提升树 GBDT案例详解

章节内容

上节完成了如下的内容：

Spark Graph X
基本概述
架构基础
概念详解
核心数据结构

编写 Spark GraphX 程序注意的事情

数据分区与负载均衡

1. 分区策略的重要性

在 GraphX 分布式图计算框架中，数据分区是性能优化的关键环节。合理的数据分区策略能够：

减少节点间的网络通信开销
提高计算资源的利用率
降低数据倾斜带来的性能影响
优化迭代计算过程中的数据交换

2. 常见分区方法

GraphX 提供了多种内置分区策略：

2.1 边分区 (EdgePartition)

这是 GraphX 的默认分区方式，特点包括：

基于边的哈希值进行分区
每个分区包含完整的顶点信息
实现简单但可能导致数据倾斜

2.2 顶点分区 (VertexPartition)

基于顶点 ID 进行分区
适合顶点度分布不均匀的图
需要配合 2D 分区策略使用

2.3 2D 分区

同时考虑边和顶点的分布
将顶点和边都划分到不同的分区中
显著减少计算过程中的通信量

3. 负载均衡优化技巧

针对不同场景的优化建议：

3.1 预处理阶段

使用 graph.partitionBy() 方法显式指定分区策略
对于社交网络图，推荐使用 PartitionStrategy.EdgePartition2D
对于二分图，考虑使用 PartitionStrategy.RandomVertexCut

3.2 运行时监控

scala 复制代码

// 检查分区情况示例
val partitions = graph.edges.partitions.size
println(s"当前分区数: $partitions")

// 检查各分区数据量
graph.edges.mapPartitions(iter => Iterator(iter.size)).collect()

3.3 应对数据倾斜

当出现数据倾斜时，可以：

使用 repartition() 方法重新分配数据
自定义分区器实现更均衡的分布
对高度数顶点采用特殊处理策略

4. 实际应用案例

在 PageRank 算法实现中：

采用 2D 分区策略可以减少约 30% 的网络传输
迭代计算时每个分区的负载更加均衡
整体计算时间可缩短 20-40%

5. 高级分区策略

对于特殊场景，还可以考虑：

基于社区发现的分区方法
动态调整分区策略
混合分区方案（如核心-边缘分区）

处理大规模数据时的内存管理

GraphX 会对顶点和边的数据进行分区和缓存，但在处理大规模图数据时，内存管理尤为重要。需要注意内存使用情况，合理配置 Spark 的内存参数，避免内存溢出或垃圾回收频繁的问题。

迭代计算的收敛条件

许多图算法（如 PageRank）是基于迭代计算的，因此要合理设置收敛条件（例如迭代次数或结果变化阈值）。过多的迭代会浪费计算资源，过少的迭代可能导致结果不准确。

图的变换和属性操作

在对图进行操作时，特别是更新顶点和边的属性时，要确保变换操作不会导致数据不一致或图结构的破坏。使用 mapVertices、mapEdges 等操作时，要谨慎处理每个顶点和边的属性。

错误处理与调试

在编写分布式程序时，错误处理和调试尤为重要。GraphX 的操作涉及复杂的图结构，调试时应充分利用 Spark 的日志和错误信息，使用小规模数据集进行初步验证，逐步扩展到大规模数据。

数据存储与序列化

GraphX 在处理大规模图数据时，可能需要将数据保存到外部存储中（如 HDFS）。要注意选择合适的数据格式和序列化方式，以保证数据读写的高效性和可靠性。

扩展性与性能优化

在开发 GraphX 应用时，考虑到未来可能的扩展需求，程序设计应具有一定的扩展性。同时，针对性能的优化也是关键，要通过测试和调整参数来找到最佳的执行配置。

编写 Spark GraphX 程序

以下是编写 Spark GraphX 程序的主要步骤：

构建顶点和边 RDD

顶点和边是构建图的基本元素。我们可以通过 RDD 来定义这些元素

scala 复制代码

// 顶点RDD (VertexId, 属性)
val vertices: RDD[(VertexId, String)] = sc.parallelize(Array(
  (1L, "Alice"), 
  (2L, "Bob"), 
  (3L, "Charlie"), 
  (4L, "David")
))

// 边RDD (源顶点ID, 目标顶点ID, 属性)
val edges: RDD[Edge[Int]] = sc.parallelize(Array(
  Edge(1L, 2L, 1), 
  Edge(2L, 3L, 1), 
  Edge(3L, 4L, 1), 
  Edge(4L, 1L, 1)
))

构建图 (Graph)

使用顶点和边的 RDD 来构建图。

scala 复制代码

val graph = Graph(vertices, edges)

进行图操作或算法计算

你可以对图进行各种操作或使用图算法库进行计算。下面的示例是计算 PageRank。

scala 复制代码

val ranks = graph.pageRank(0.01).vertices

收集和处理结果

通过 collect 或 saveAsTextFile 等方法获取和处理计算结果。

scala 复制代码

ranks.collect().foreach { case (id, rank) => 
  println(s"Vertex $id has rank: $rank") 
}

关闭 SparkContext

在程序结束时，关闭 SparkContext 以释放资源。

scala 复制代码

sc.stop()

导入依赖

xml 复制代码

<dependency>
  <groupId>org.apache.spark</groupId>
  <artifactId>spark-graphx_2.12</artifactId>
  <version>${spark.version}</version>
</dependency>

案例一：图的基本计算

编写代码

scala 复制代码

package icu.wzk
object GraphExample1 {

  def main(args: Array[String]): Unit = {
    val conf = new SparkConf()
      .setAppName("GraphExample1")
      .setMaster("local[*]")
    val sc = new SparkContext(conf)
    sc.setLogLevel("WARN")

    // 初始化数据
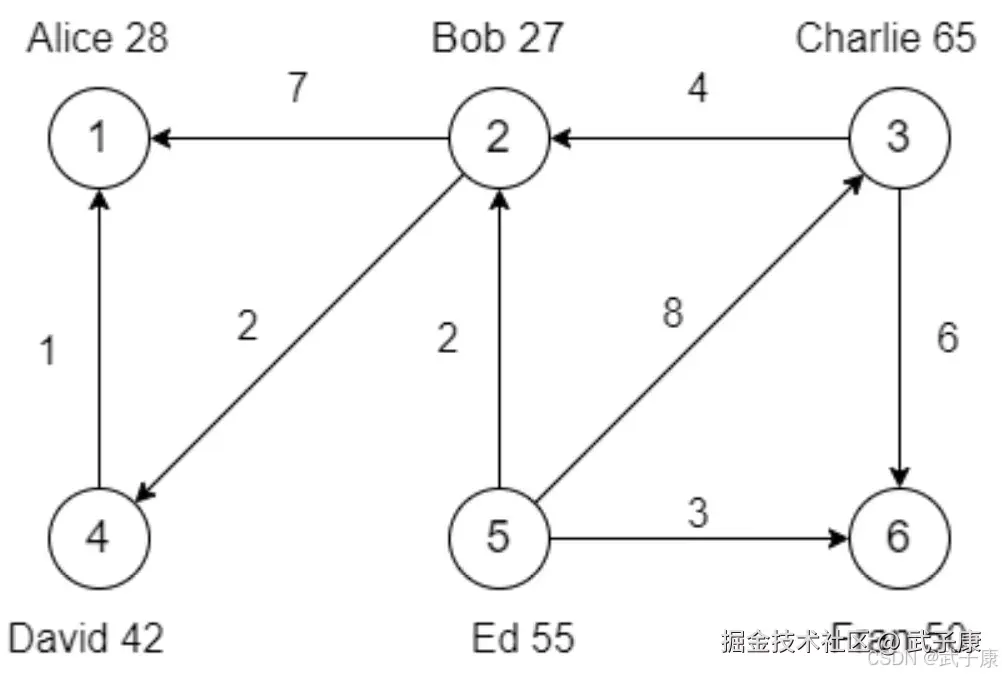
    // 定义定点（Long，info）
    val vertexArray: Array[(VertexId, (String, Int))] = Array(
      (1L, ("Alice", 28)),
      (2L, ("Bob", 27)),
      (3L, ("Charlie", 65)),
      (4L, ("David", 42)),
      (5L, ("Ed", 55)),
      (6L, ("Fran", 50))
    )

    // 定义边（Long，Long，attr）
    val edgeArray: Array[Edge[Int]] = Array(
      Edge(2L, 1L, 7),
      Edge(2L, 4L, 2),
      Edge(3L, 2L, 4),
      Edge(3L, 6L, 3),
      Edge(4L, 1L, 1),
      Edge(5L, 2L, 2),
      Edge(5L, 3L, 8),
      Edge(5L, 6L, 3),
    )

    // 构造vertexRDD和edgeRDD
    val vertexRDD: RDD[(Long, (String, Int))] = sc.makeRDD(vertexArray)
    val edgeRDD: RDD[Edge[Int]] = sc.makeRDD(edgeArray)

    // 构造图Graph[VD,ED]
    val graph: Graph[(String, Int), Int] = Graph(vertexRDD, edgeRDD)

    // 属性操作实例
    // 找出图中年龄大于30的顶点
    graph.vertices
      .filter {
        case (_, (_, age)) => age > 30
      }
      .foreach(println)

    // 找出图中属性大于5的边
    graph.edges
      .filter {
        edge => edge.attr > 5
      }
      .foreach(println)

    // 列出边属性 > 5 的triplets
    graph.triplets
      .filter(t => t.attr > 5)
      .foreach(println)

    // degrees操作
    // 找出图中最大的出度、入度、度数
    println("==========outDegrees=============")
    graph.outDegrees.foreach(println)
    val outDegrees: (VertexId, Int) = graph.outDegrees
      .reduce {
        (x, y) => if (x._2 > y._2) x else y
      }
    println(s"Out degree: ${outDegrees}")

    println("==========inDegrees=============")
    graph.inDegrees.foreach(println)
    val inDegrees: (VertexId, Int) = graph.inDegrees
      .reduce {
        (x, y) => if (x._2 > y._2) x else y
      }
    println(s"In degree: ${inDegrees}")

    // 转换操作
    // 顶点的转换操作 所有人年龄+10岁
    graph.mapVertices {
      case (id, (name, age)) => (id, (name, age + 10))
    }
      .vertices
      .foreach(println)

    // 边的转换操作 边的属性 * 2
    graph.mapEdges(e => e.attr * 2)
      .edges
      .foreach(println)

    // 结构操作
    // 顶点年龄 > 30的子图
    val subGraph: Graph[(String, Int), Int] = graph.subgraph(vpred = (id, vd) => vd._2 >= 30)
    println("==========SubGraph=============")
    subGraph.vertices.foreach(println)
    subGraph.edges.foreach(println)

    // 连接操作
    println("============连接操作==============")
    // 创建一个新图 顶点VD的数据类型 User，并从Graph做类型转换
    val initialUserGraph: Graph[User, Int] = graph.mapVertices {
      case (_, (name, age)) => User(name, age, 0, 0)
    }
    // initialUserGraph 与 inDegree outDegree 进行 JOIN 修改 inDeg outDeg
    var userGraph: Graph[User, Int] = initialUserGraph
      .outerJoinVertices(initialUserGraph.inDegrees) {
        case (id, u, inDegOut) => User(u.name, u.age, inDegOut.getOrElse(0), u.outDeg)
      }
      .outerJoinVertices(initialUserGraph.outDegrees) {
        case (id, u, outDegOut) => User(u.name, u.age, u.inDeg, outDegOut.getOrElse(0))
      }

    userGraph.vertices.foreach(println)

    // 找到 出度=入度 的人员
    userGraph.vertices
      .filter {
      case (id, u) => u.inDeg == u.outDeg
    }
      .foreach(println)

    // 聚合操作
    // 找到5到各顶点的最短距离
    // 定义源点
    val sourceId: VertexId = 5L
    val initialGraph: Graph[Double, Int] = graph
      .mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)
    val sssp: Graph[Double, Int] = initialGraph.pregel(Double.PositiveInfinity)(
      // 两个消息来的时候，取它们当中路径的最小值
      (id, dist, newDist) => math.min(dist, newDist),
      // Send Message 函数
      // 比较 triplet.srcAttr + triplet.attr 和 triplet.dstAttr
      // 如果小于，则发送消息到目的顶点
      triplet => {
        // 计算权重
        if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {
          Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))
        } else {
          Iterator.empty
        }
      },
      // mergeMsg
      (a, b) => Math.min(a, b)
    )

    println("找到5到各个顶点的最短距离")
    println(sssp.vertices.collect.mkString("\n"))

    sc.stop()

  }
}

case class User(name: String, age: Int, inDeg: Int, outDeg: Int)

运行结果

运行截图如下：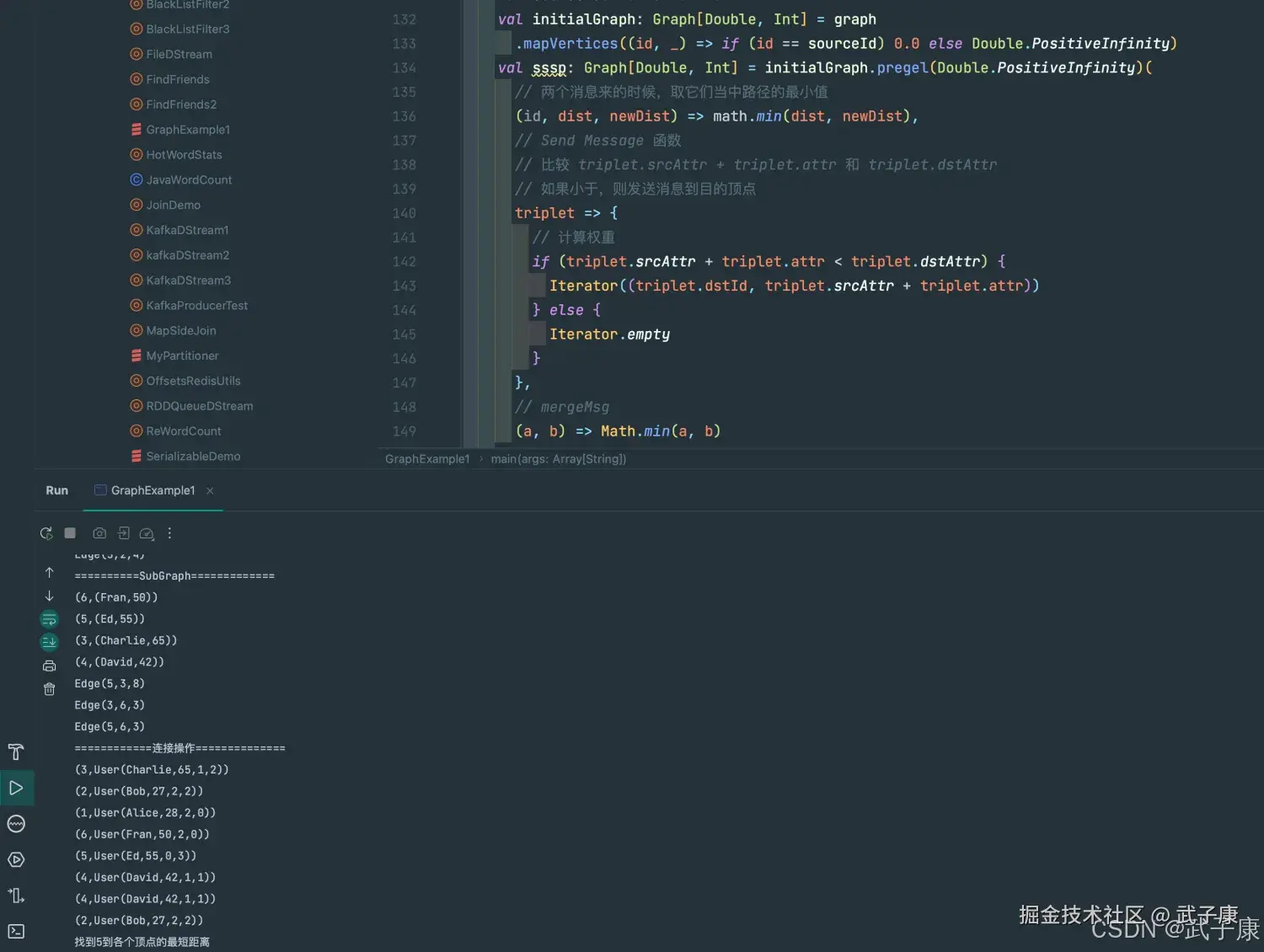

Pregel API

图本身是递归数据结构，顶点的属性依赖于它们的邻居的属性，这些邻居的属性又依赖于自己的邻居的属性。所以需要重要的算法都是迭代的重新计算每个顶点的属性，直到满足某个确定的条件。一系列的图并发抽象被提出来用来表达这些迭代算法。 GraphX公开了一个类似Pregel的操作

vprog：用户定义的顶点运行程序，它所用每一个顶点，负责接收进来的信息，并计算新的顶点值
sendMsg：发送消息
mergeMsg：合并消息

案例二：连通图算法

给定数据文件，找到存在的连通体

数据内容

自己生成一些即可：

shell 复制代码

编写代码

scala 复制代码

package icu.wzk
object GraphExample2 {

  def main(args: Array[String]): Unit = {
    val conf = new SparkConf()
      .setAppName("GraphExample2")
      .setMaster("local[*]")
    val sc = new SparkContext(conf)
    sc.setLogLevel("WARN")

    // 从数据文件中加载 生成图
    val graph: Graph[Int, Int] = GraphLoader.edgeListFile(sc, "graph.txt")
    graph.vertices.foreach(println)
    graph.edges.foreach(println)
    // 生成连通图
    graph.connectedComponents()
      .vertices
      .sortBy(_._2)
      .foreach(println)

    // 关闭 SparkContext
    sc.stop()
  }
}

运行结果

运行截图如下所示：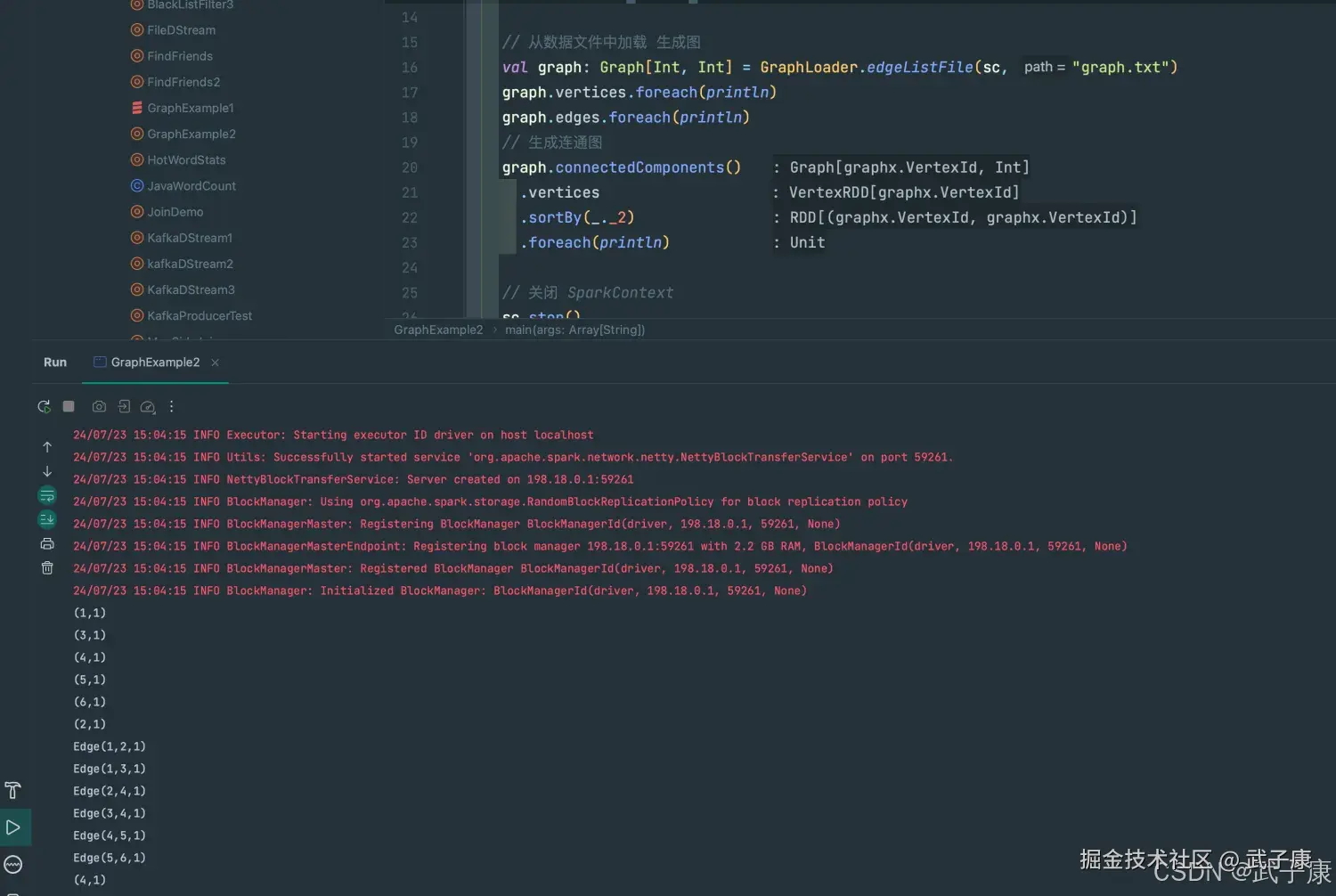

案例三：寻找相同的用户，合并信息

需求明确

假设：

假设五个不同信息可以作为用户标识，分别：1X，2X，3X，4X，5X
每次可以选择使用若干为字段作为标识
部分标识可能发生变化，如 12变为13 或 24变为25

根据以上规则，判断以下标识是否代表同一用户：

11-21-32、12-22-33（X）
11-21-32、11-21-52（OK）
21-32、11-21-33（OK）
11-21-32、32-48（OK）

问题：在以下数据中，找到同一个用户，合并相同用户的数据

对于用户标识（id）：合并后去重
对于用户的信息：key相同，合并权重

编写代码

scala 复制代码

package icu.wzk
object GraphExample3 {

  def main(args: Array[String]): Unit = {
    val conf = new SparkConf()
      .setAppName("GraphExample3")
      .setMaster("local[*]")
    val sc = new SparkContext(conf)
    sc.setLogLevel("WARN")

    val dataRDD: RDD[(List[Long], List[(String, Double)])] = sc.makeRDD(
      List(
        (List(11L, 21L, 31L), List("kw$北京" -> 1.0, "kw$上海" -> 1.0, "area$中关村" -> 1.0)),
        (List(21L, 32L, 41L), List("kw$上海" -> 1.0, "kw$天津" -> 1.0, "area$回龙观" -> 1.0)),
        (List(41L), List("kw$天津" -> 1.0, "area$中关村" -> 1.0)),
        (List(12L, 22L, 33L), List("kw$大数据" -> 1.0, "kw$spark" -> 1.0, "area$西二旗" -> 1.0)),
        (List(22L, 34L, 44L), List("kw$spark" -> 1.0, "area$五道口" -> 1.0)),
        (List(33L, 53L), List("kw$hive" -> 1.0, "kw$spark" -> 1.0, "area$西二旗" -> 1.0))
      )
    )

    // 1 将标识信息中的每一个元素抽取出来，作为ID
    // 备注1 这里使用了 flatMap 将元素压平
    // 备注2 这里丢掉了标签信息，因为这个RDD主要用于构造顶点、边
    // 备注3 顶点、边的数据要求Long，这个程序修改后才能用在我们的程序中
    val dotRDD: RDD[(VertexId, VertexId)] = dataRDD.flatMap {
      case (allids, _) => allids.map(id => (id, allids.mkString.hashCode.toLong))
    }

    // 2 定义顶点
    val vertexesRDD: RDD[(VertexId, String)] = dotRDD.map {
      case (id, _) => (id, "")
    }
    // 3 定义边(id: 单个标识信息：ids：全部的标识信息)
    val edgesRDD: RDD[Edge[Int]] = dotRDD.map {
      case (id, ids) => Edge(id, ids, 0)
    }
    // 4 生成图
    val graph = Graph(vertexesRDD, edgesRDD)
    // 5 找到强连通体
    val connectRDD: VertexRDD[VertexId] = graph.connectedComponents().vertices;
    // 6 定义中心点的数据
    val centerVertexRDD: RDD[(VertexId, (List[VertexId], List[(String, Double)]))] = dataRDD.map {
      case (allIds, tags) => (allIds.mkString.hashCode.toLong, (allIds, tags))
    }
    // 7 步骤5、6的数据做join 获取需要合并的数据
    val allInfoRDD = connectRDD.join(centerVertexRDD).map {
      case (_, (id2, (allIds, tags))) => (id2, (allIds, tags))
    }
    // 8 数据聚合（将同一个用户的标识、标签放在一起）
    val mergeInfoRDD: RDD[(VertexId, (List[VertexId], List[(String, Double)]))] = allInfoRDD
      .reduceByKey {
        case ((bufferList, bufferMap), (allIds, tags)) =>
          val newList = bufferList ++ allIds

          // map 合并
          val newMap = bufferMap ++ tags
          (newList, newMap)
      }

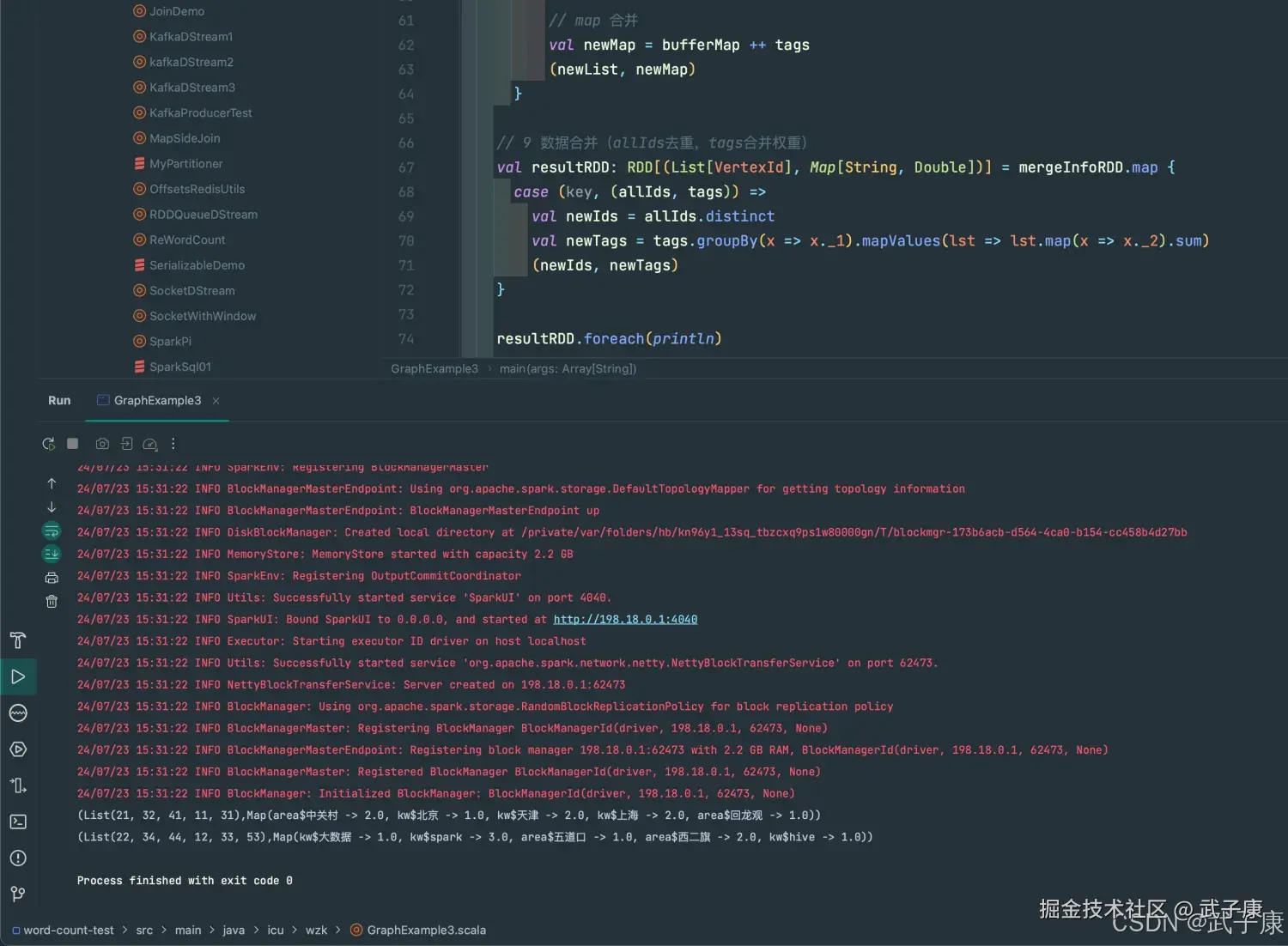
    // 9 数据合并（allIds去重，tags合并权重）
    val resultRDD: RDD[(List[VertexId], Map[String, Double])] = mergeInfoRDD.map {
      case (key, (allIds, tags)) =>
        val newIds = allIds.distinct
        val newTags = tags.groupBy(x => x._1).mapValues(lst => lst.map(x => x._2).sum)
        (newIds, newTags)
    }

    resultRDD.foreach(println)

    sc.stop()
  }

}

运行结果

运行的截图如下图：

大数据-106 Spark Graph X案例：1图计算、2连通图算法、3寻找相同用户 高效分区、负载均衡与迭代优化

点一下关注吧！！！非常感谢！！持续更新！！！

🚀 AI篇持续更新中！（长期更新）

💻 Java篇正式开启！（300篇）

📊 大数据板块已完成多项干货更新（300篇）：

章节内容

编写 Spark GraphX 程序注意的事情

数据分区与负载均衡

1. 分区策略的重要性

2. 常见分区方法

2.1 边分区 (EdgePartition)

2.2 顶点分区 (VertexPartition)

2.3 2D 分区

3. 负载均衡优化技巧

3.1 预处理阶段

3.2 运行时监控

3.3 应对数据倾斜

4. 实际应用案例

5. 高级分区策略

处理大规模数据时的内存管理

迭代计算的收敛条件

图的变换和属性操作

错误处理与调试

数据存储与序列化

扩展性与性能优化

编写 Spark GraphX 程序

构建顶点和边 RDD

构建图 (Graph)

进行图操作或算法计算

收集和处理结果

关闭 SparkContext

导入依赖

案例一：图的基本计算

编写代码

运行结果

Pregel API

案例二：连通图算法

数据内容

编写代码

运行结果

案例三：寻找相同的用户，合并信息

需求明确

编写代码

运行结果

大数据-106 Spark Graph X案例：1图计算、2连通图算法、3寻找相同用户高效分区、负载均衡与迭代优化