secp256k1算法详解四（关键点补充说明）

1 magnitude及normalized

由于当前许多项目都用到secp256k1库，比特币作为体量最大的数字货币项目，这里建议直接参考bitcoin-core提供的最新secp256k1源码。仍以field的10x26实现版本为例，相关定义如下：

/** This field implementation represents the value as 10 uint32_t limbs in base
 *  2^26. */
typedef struct {
   /* A field element f represents the sum(i=0..9, f.n[i] << (i*26)) mod p,
    * where p is the field modulus, 2^256 - 2^32 - 977.
    *
    * The individual limbs f.n[i] can exceed 2^26; the field's magnitude roughly
    * corresponds to how much excess is allowed. The value
    * sum(i=0..9, f.n[i] << (i*26)) may exceed p, unless the field element is
    * normalized. */
    uint32_t n[10];
    /*
     * Magnitude m requires:
     *     n[i] <= 2 * m * (2^26 - 1) for i=0..8
     *     n[9] <= 2 * m * (2^22 - 1)
     *
     * Normalized requires:
     *     n[i] <= (2^26 - 1) for i=0..8
     *     sum(i=0..9, n[i] << (i*26)) < p
     *     (together these imply n[9] <= 2^22 - 1)
     */
    SECP256K1_FE_VERIFY_FIELDS
} secp256k1_fe;

对于magnitude，可称其为"量级"，当m=0时，这时n[i] <= 0(i=0...9)，由此可知此时secp256k1_fe大数必为0，当m=1时，n[i] <= 2*(2^26 - 1)对于i=0...8，n[9] <= 2*(2^22 - 1)，有些说法是当m=1时，是将大数限制到[0,到2p)范围内，这是不准确的，此时secp256k1_fe大数范围是[0, 2*(2^256-1)]（上限是稍大于2p的），magnitude设计本质是"存储约束"而非"模p范围"，通过magnitude约束将大数控制在可高效约简的范围内，magnitude表示大概是2m个p的量级。

对于normalized，可称其为"规范化（归一化）"，从注释中可知每个n[i]都小于或等于其对应的MASK，且sum(n[i]) < p，即规范化后的大数是[0, p)之内的数。由此可知规范化的大数一定是magnitude为0或1的数，但是magnitude为1的数不一定是规范化的大数。

函数secp256k1_fe_normalize对大数实现规范化操作，其本质是将大数看作为特殊的2^26进制大数，即N=∑n_i*w_i，这里n_i <= 2 * m * (2^26 - 1) for i=0..8，n₉ <= 2 * m * (2^22 - 1)，w_i=2^(i*26)，之所以说它特殊，是因为由于m的存在，每个位上数值是可以大于或等于基数2^26的（正常情况下每个位上取值小于基数，如10进制数，每个位上数值都小于基数10，另外最高位取值有特殊限制），在secp256k1_fe_normalize函数中有两部分操作，第一部分先将大数A规范为最多为257位的大数B（m确定时，该数对应确定最大值，后续详解），第二部分将大数B规范为小于模数p的大数。

在secp256k1源码中其实定义了各个参数大数中magnitude的最大值，在定义VERIFY宏时会对参数合法性进行检查。

#define SECP256K1_GE_X_MAGNITUDE_MAX  4
#define SECP256K1_GE_Y_MAGNITUDE_MAX  3
#define SECP256K1_GEJ_X_MAGNITUDE_MAX 4
#define SECP256K1_GEJ_Y_MAGNITUDE_MAX 4
#define SECP256K1_GEJ_Z_MAGNITUDE_MAX 1

由以上定义可知，在secp256k1算法中0 <= m <= 4，当m=0时，显而易见大数即为0，当m>=1且m<=4时，其实大数对应最大值分别为：

pow(2,256)-1)*2*1=0x1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffe
pow(2,256)-1)*2*2=0x3fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffc
pow(2,256)-1)*2*3=0x5fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffa
pow(2,256)-1)*2*4=0x7fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff8

当m取值为4时对应最大值在调用规范化函数时，第一部分规范完以后对应最大值为0x100003c00000f000000000001e000003c00000f000003c00000f0000f3c00393e，为一个257位的大数，函数secp256k1_fe_normalize_weak其实就是secp256k1_fe_normalize第一部分执行完以后的输出，该值就是weak函数在m<=4下输出的最大值，该值本身为m<=1的大数。

2 常用函数magnitude值分析

先分析大数取反原型函数secp256k1_fe_negate，其原型如下：

SECP256K1_INLINE static void secp256k1_fe_negate(secp256k1_fe *r, const secp256k1_fe *a, int m) {
    r->n[0] = 0x3FFFC2FUL * 2 * (m + 1) - a->n[0];
    r->n[1] = 0x3FFFFBFUL * 2 * (m + 1) - a->n[1];
    r->n[2] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[2];
    r->n[3] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[3];
    r->n[4] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[4];
    r->n[5] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[5];
    r->n[6] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[6];
    r->n[7] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[7];
    r->n[8] = 0x3FFFFFFUL * 2 * (m + 1) - a->n[8];
    r->n[9] = 0x03FFFFFUL * 2 * (m + 1) - a->n[9];
}

这里m是输入参数a的magnitude，当m=0时，输出参数r为2p，显然其对应的m'=1；当输入参数a的m=1时，其取值范围为[1, 0x1fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffe]，则2*(m+1)*p-a取值范围是[0x1fffffffffffffffffffffffffffffffffffffffffffffffffffffffbfffff0be, 0x3fffffffffffffffffffffffffffffffffffffffffffffffffffffffbfffff0bb]，所以输出r的m'<=2，所以对于任意输入m，输出r的m'<=m+1。

对于secp256k1_fe_add函数，其源码如下：

SECP256K1_INLINE static void secp256k1_fe_add(secp256k1_fe *r, const secp256k1_fe *a) {
    SECP256K1_FE_VERIFY(r);
    SECP256K1_FE_VERIFY(a);
    VERIFY_CHECK(r->magnitude + a->magnitude <= 32);

    secp256k1_fe_impl_add(r, a);
    r->magnitude += a->magnitude;
    r->normalized = 0;

    SECP256K1_FE_VERIFY(r);
}

secp256k1_fe_add

显而易见，对于输出r来说m(r)<=m(r)+m(a)，r和a都是secp256k1_fe型数据。

对于secp256k1_fe_mul_int(r, a)，a为int型数据，m(r)<=m(r)*a。

对于secp256k1_fe_mul/secp256k1_fe_sqr函数，在实现中包含内部规约，会把输出参数的"量级"规约回magnitude = 1，使输出可以当作normalized-like使用。

下面以函数为例给出各个步骤的详细magnitude值：

static void secp256k1_gej_add_var(secp256k1_gej *r, const secp256k1_gej *a, const secp256k1_gej *b, secp256k1_fe *rzr) {
    /* 12 mul, 4 sqr, 11 add/negate/normalizes_to_zero (ignoring special cases) */
    secp256k1_fe z22, z12, u1, u2, s1, s2, h, i, h2, h3, t;
    SECP256K1_GEJ_VERIFY(a);
    SECP256K1_GEJ_VERIFY(b);

    if (a->infinity) {
        VERIFY_CHECK(rzr == NULL);
        *r = *b;
        return;
    }
    if (b->infinity) {
        if (rzr != NULL) {
            secp256k1_fe_set_int(rzr, 1);
        }
        *r = *a;
        return;
    }

    secp256k1_fe_sqr(&z22, &b->z);
    secp256k1_fe_sqr(&z12, &a->z);
    secp256k1_fe_mul(&u1, &a->x, &z22);
    secp256k1_fe_mul(&u2, &b->x, &z12);
    secp256k1_fe_mul(&s1, &a->y, &z22); secp256k1_fe_mul(&s1, &s1, &b->z);
    secp256k1_fe_mul(&s2, &b->y, &z12); secp256k1_fe_mul(&s2, &s2, &a->z);
    secp256k1_fe_negate(&h, &u1, 1); secp256k1_fe_add(&h, &u2);
    secp256k1_fe_negate(&i, &s2, 1); secp256k1_fe_add(&i, &s1);
    if (secp256k1_fe_normalizes_to_zero_var(&h)) {
        if (secp256k1_fe_normalizes_to_zero_var(&i)) {
            secp256k1_gej_double_var(r, a, rzr);
        } else {
            if (rzr != NULL) {
                secp256k1_fe_set_int(rzr, 0);
            }
            secp256k1_gej_set_infinity(r);
        }
        return;
    }

    r->infinity = 0;
    secp256k1_fe_mul(&t, &h, &b->z);
    if (rzr != NULL) {
        *rzr = t;
    }
    secp256k1_fe_mul(&r->z, &a->z, &t);

    secp256k1_fe_sqr(&h2, &h);
    secp256k1_fe_negate(&h2, &h2, 1);
    secp256k1_fe_mul(&h3, &h2, &h);
    secp256k1_fe_mul(&t, &u1, &h2);

    secp256k1_fe_sqr(&r->x, &i);
    secp256k1_fe_add(&r->x, &h3);
    secp256k1_fe_add(&r->x, &t);
    secp256k1_fe_add(&r->x, &t);

    secp256k1_fe_add(&t, &r->x);
    secp256k1_fe_mul(&r->y, &t, &i);
    secp256k1_fe_mul(&h3, &h3, &s1);
    secp256k1_fe_add(&r->y, &h3);

    SECP256K1_GEJ_VERIFY(r);
}

secp256k1_gej_add_var

首先以输入参数a，b中的x，y，z都为magnitude=1（normalized-like）为前提，在此基础上给出按代码顺序的表：

步	代码（操作）	输入 m	输出 m（上限）	说明
1	secp256k1_fe_sqr(&z22, &b->z)	b->z:1	1	fe_sqr → 规约为 1
2	secp256k1_fe_sqr(&z12, &a->z)	a->z:1	1
3	secp256k1_fe_mul(&u1, &a->x, &z22)	1,1	1	fe_mul → 规约为 1
4	secp256k1_fe_mul(&u2, &b->x, &z12)	1,1	1
5	secp256k1_fe_mul(&s1, &a->y, &z22)	1,1	1
6	secp256k1_fe_mul(&s1, &s1, &b->z)	1,1	1
7	secp256k1_fe_mul(&s2, &b->y, &z12)	1,1	1
8	secp256k1_fe_mul(&s2, &s2, &a->z)	1,1	1
9	secp256k1_fe_negate(&h, &u1, 1)	u1:1	2	fe_negate → m_out = 1 + 1 = 2
10	secp256k1_fe_add(&h, &u2)	h:2, u2:1	3	fe_add: 2 + 1 = 3
11	secp256k1_fe_negate(&i, &s2, 1)	s2:1	2
12	secp256k1_fe_add(&i, &s1)	i:2, s1:1	3
13	if (secp256k1_fe_normalizes_to_zero_var(&h)) ...	---	---	特殊分支（不进入一般流程）
14	secp256k1_fe_mul(&t, &h, &b->z)	h:3, b.z:1	1	fe_mul → 规约为 1
15	if (rzr != NULL) *rzr = t;	t:1	1
16	secp256k1_fe_mul(&r->z, &a->z, &t)	a.z:1, t:1	1
17	secp256k1_fe_sqr(&h2, &h)	h:3	1	fe_sqr → 规约为 1
18	secp256k1_fe_negate(&h2, &h2, 1)	h2:1	2
19	secp256k1_fe_mul(&h3, &h2, &h)	h2:2, h:3	1	fe_mul → 规约为 1
20	secp256k1_fe_mul(&t, &u1, &h2)	u1:1, h2:2	1
21	secp256k1_fe_sqr(&r->x, &i)	i:3	1
22	secp256k1_fe_add(&r->x, &h3)	r->x:1, h3:1	2
23	secp256k1_fe_add(&r->x, &t)	r->x:2, t:1	3
24	secp256k1_fe_add(&r->x, &t)	r->x:3, t:1	4
25	secp256k1_fe_add(&t, &r->x)	t:1, r->x:4	5	（t 被覆盖为 t + r->x）
26	secp256k1_fe_mul(&r->y, &t, &i)	t:5, i:3	1	fe_mul → 规约为 1
27	secp256k1_fe_mul(&h3, &h3, &s1)	h3:1, s1:1	1
28	secp256k1_fe_add(&r->y, &h3)	r->y:1, h3:1	2
29	函数返回	r->x:4, r->y:2, r->z:1	---	这些是按最小合法上界得到的值（未再 normalize 前）

由表可知对于secp256k1_gej_add_var函数，虽然运行过程中，零时变量可能会出现相对较高的magnitude值，但最终返回值r->x的magnitude值是满足SECP256K1_GE_X_MAGNITUDE_MAX值的，同理y，z也满足SECP256K1_GEJ_Y_MAGNITUDE_MAX和SECP256K1_GEJ_Z_MAGNITUDE_MAX限制。

3 大数求逆

最新版大数求逆函数实现原型如下：

1 static void secp256k1_fe_impl_inv(secp256k1_fe *r, const secp256k1_fe *x) {
2     secp256k1_fe tmp = *x;
3     secp256k1_modinv32_signed30 s;
4 
5     secp256k1_fe_normalize(&tmp);
6     secp256k1_fe_to_signed30(&s, &tmp);
7     secp256k1_modinv32(&s, &secp256k1_const_modinfo_fe);
8     secp256k1_fe_from_signed30(r, &s);
9 }

3.1 高层概览

1. 主要步骤

函数做的是对域元素x求模逆，即求r = x^-1 mod p，这里p = 2^256 - 2^32 - 977，其实现流程如下：

1）先把tmp（x）规范化，保证tmp是库约定的limb范围下唯一表示；

2）把规范化的tmp（10x26-bit limbs）转换成一种signed30的中间表示（若干个30-bit的有符号limbs），以便后面用32-bit算法实现逆元算法；

3）在signed30表示上运行secp256k1_modinv32------这是一个针对30-bit/32-bit limbs优化、并做过constant-time处理的模逆实现，基于safegcd/division-steps（改进的欧几里得/半GCD）的思想；

4）把得到的signed30结果再转换回库的secp256k1_fe（10x26表示），并写入r（该转换同时完成必要的约减/规范化）。

2. divsteps算法

divsteps是一种高效计算GCD（Greatest Common Divisor最大公约数）的方法，它通过连续多次除法步骤减少迭代次数，特别适合硬件实现和大数计算。它是GCD算法的优化版本，主要特点：

• 利用二进制表示的优势，通过右移操作快速消除因子2
• 一次迭代处理多个 "减法 - 移位" 步骤，减少循环次数
• 使用比较和差值运算替代昂贵的除法操作

求u和v最大公约数算法步骤如下：

1）消除因子2

• 统计并移除两数中的所有因子2
• 设a = u / 2^sa，b = v / 2^sb（这里sa是u可整除2的最大次数，sb是v可整除2的最大次数）

2）divsteps迭代

• 比较a和b
• 计算差值d = | a - b |
• 消除d中的所有因子2得到d'
• 用min(a, b)和d'替换(a, b)
• 重复直到a == b

3）得出最终结果

gcd(u, v) = b * 2^min(sa, sb)

算法基于以下假设：如果gcd(u, v)是最大公约数，那么它可以分成两部分的乘积，一部分是2的整数次幂，另一部分是非2的倍数。步骤1其实是获取u、v最大公因数中能2整数次幂部分，即2^min(sa, sb)^，步骤2获取非2的倍数部分。步骤1比较好理解，这里分析下步骤2，假设得出最后一步结论a==b时，具体值为a'，b'，则a'必然满足a' - b' = b'*2^x，则有a' = b'*(1+2^x)，即a'是b'的倍数，则在上一步必有d'=b'*2^y = a'' - a'，由此a'' = a' + b'*2^y，即a''也为b的倍数，由此类推，可知最一开始的a和b闭然都是b'的倍数。由以上推理可知最终gcd(u, v) = b' * 2^min(sa, sb)。

以下是算法示例代码：

#include <stdint.h>
#include <stdlib.h>

// 计算二进制表示中后缀0的个数
static int count_trailing_zeros(uint64_t x) {
    if (x == 0) return 64;
    int cnt = 0;
    while ((x & 1) == 0) {
        cnt++;
        x >>= 1;
    }
    return cnt;
}

uint64_t gcd_divsteps(uint64_t u, uint64_t v) {
    if (u == 0) return v;
    if (v == 0) return u;

    // 步骤1: 移除所有因子2
    int sa = count_trailing_zeros(u);
    int sb = count_trailing_zeros(v);
    u >>= sa;
    v >>= sb;

    // 步骤2: divsteps迭代
    while (u != v) {
        if (u < v) { uint64_t t = u; u = v; v = t; }  // 确保u >= v
        
        uint64_t d = u - v;
        int sd = count_trailing_zeros(d);
        d >>= sd;  // 一次消除所有因子2
        
        u = d;
    }

    // 步骤3: 恢复共同的因子2
    return u << (sa < sb ? sa : sb);
}

divsteps

计算示例：gcd(270, 324)：

1）初始值：u=270，v=324

2）移除因子2：sa=1，sb=2 → u=135, v=81

3）第一次迭代：

• d=135-81=54
• 移除因子2: sd=1 → d=27
• 新值: u=81, v=27

4）第二次迭代：

• d=81-27=54
• 移除因子2: sd=1 → d=27
• 新值: u=27, v=27

5）循环结束，结果：gcd(270, 324) = 27*2^1 = 54。

3.2 逐步详解

步骤1将大数进行规范化，这一步由secp256k1_fe_normalize实现，该函数已经在之前文章中详细介绍，这里不再进行分析。

步骤2调用secp256k1_fe_to_signed30函数实现，该函数源码如下：

static void secp256k1_fe_to_signed30(secp256k1_modinv32_signed30 *r, const secp256k1_fe *a) {
    const uint32_t M30 = UINT32_MAX >> 2;
    const uint64_t a0 = a->n[0], a1 = a->n[1], a2 = a->n[2], a3 = a->n[3], a4 = a->n[4],
                   a5 = a->n[5], a6 = a->n[6], a7 = a->n[7], a8 = a->n[8], a9 = a->n[9];

    r->v[0] = (a0       | a1 << 26) & M30;
    r->v[1] = (a1 >>  4 | a2 << 22) & M30;
    r->v[2] = (a2 >>  8 | a3 << 18) & M30;
    r->v[3] = (a3 >> 12 | a4 << 14) & M30;
    r->v[4] = (a4 >> 16 | a5 << 10) & M30;
    r->v[5] = (a5 >> 20 | a6 <<  6) & M30;
    r->v[6] = (a6 >> 24 | a7 <<  2
                        | a8 << 28) & M30;
    r->v[7] = (a8 >>  2 | a9 << 24) & M30;
    r->v[8] =  a9 >>  6;
}

secp256k1_fe_to_signed30

该函数实现很清晰，就是把原有的10个无符号26bit数重新按30bit窗口打包到一组32-bit有符号整数中（共9个元素，每个元素保存30位有效位，并且用int32_t保存以允许出现负数中间值）。

步骤3调用secp256k1_modinv32函数求模逆，该步骤是算法的核心，后续详细解析。

步骤4调用secp256k1_fe_from_signed30函数将30bit格式逆元再转换到标准10x26bit形式。

1. 扩展欧几里得算法

扩展欧几里得定理：对于任意整数a和b，必然存在整数x和y满足贝祖等式：a·x + b·y = gcd(a, b)，且gcd(a, b)是能表示为a·x + b·y形式的最小正整数。

1）基础引理：欧几里得算法的余数性质

欧几里得算法通过反复求余计算GCD：

gcd(a, b) = gcd(b, a mod b)

其中a mod b = a - b*⌊a/b⌋（⌊⌋为向下取整），且0 ≤ a mod b < |b|。

2）数学归纳法证明贝祖等式存在性

归纳基础：

当b = 0 时，gcd(a, 0) = a，此时取 x = 1，y = 0（这里y可以取任意值，只不过取0后续计算最简单），显然满足 a·1 + 0·0 = a = gcd(a, 0)。

归纳步骤：

假设对于 (b, a mod b) 存在整数 x' 和 y' 满足：b·x' + (a mod b)·y' = gcd(b, a mod b)

根据余数定义 a mod b = a - b·⌊a/b⌋，代入上式：b·x' + (a - b·⌊a/b⌋)·y' = gcd(a, b)（因 gcd(a, b) = gcd(b, a mod b)）

整理得：

a·y' + b·(x' - ⌊a/b⌋·y') = gcd(a, b)，令 x = y'，y = x' - ⌊a/b⌋·y'，则有：a·x + b·y = gcd(a, b)

因此，若 (b, a mod b) 存在解，则 (a, b) 也存在解。由数学归纳法，对任意整数 a, b 均存在这样的 x, y。

3）最小性证明

设 d = gcd(a, b)，则 d 整除 a 和 b，因此 d 整除 a·x + b·y 的所有可能结果。即任何能表示为 a·x + b·y 的整数都是 d 的倍数，故 d 是其中最小的正整数。

其实以上结论是基于一个前提：对于任意两个整数a和b，在应用欧几里得算法若干步后，都能转化成将gcd(a, b)转换成gcd(b', 0)的形式，这个结论可以自己查阅相关整理过程，又因为gcd(a, b) = gcd(-a, -b)，所以该结论对于所有非零整数都成立。

接下来看看在算法层面如何推导系数x和y：

首先，对于gcd(a, b)中的a和b来说都可以看作是各次除法迭代的"余数r"，即gcd(a, b) = gcd(b, a%b))，如果将a%b看作是new_r，b看作是r，a看作是old_r，则有：old_r = q⋅r + new_r，这里q是整数商a//b。

接下来，因为求系数x和y其实也是一个迭代推导的过程，假设当前有：

可以先把最一开始old_r和r的由系数表示出来：old_r = 1*a + 0*b，r = 0*a + 1*b，即存在初始余数对：(old_r, r) = (a, b)，初始a的系数对：(old_x, x) = (1, 0)，初始b的系数对：(old_y, y) = (0, 1)满足方程。

再接下来，继续进行迭代q = old_r//r，new_r = old_r - q*r，将(1)中old_r和(2)中的r代入该等式并进行整理可得：

由此可得：new_x = old_x - q*x，new_y = old_y - q*y，即new_r仍是a，b的线性组合，且new_x，new_y是相应系数。以下是完整算法伪代码：

(old_r, r) = (a, b)
(old_x, x) = (1, 0)  # 表示 a 的系数
(old_y, y) = (0, 1)  # 表示 b 的系数

while r ≠ 0:
    q = old_r // r
     
    # 更新余数
    (old_r, r) = (r, old_r - q * r)
    
    # 更新系数
    (old_x, x) = (x, old_x - q * x)
    (old_y, y) = (y, old_y - q * y)
   
# 最终结果   
gcd(a,b) = old_r
x = old_x, y = old_y

以a=240，b=46为例，给出算法迭代过程：

初始值：(old_r, r) = (240, 46), (old_x, x) = (1, 0), (old_y, y) = (0, 1)
第1步：240/46=5...10, q = 5, (old_r, r) = (46, 10), (old_x, x) = (0, 1), (old_y, y) = (1, -5)
第2步：46/10=4...6, q = 4, (old_r, r) = (10, 6), (old_x, x) = (1, -4), (old_y, y) = (-5, 21)
第3步：10/6=1...4, q = 1, (old_r, r) = (6, 4), (old_x, x) = (-4, 5), (old_y, y) = (21, -26)
第4步：6/4=1...2, q = 1, (old_r, r) = (4, 2), (old_x, x) = (5, -9), (old_y, y) = (-26, 47)
第5步：4/2=2...0, q = 2, (old_r, r) = (2, 0), (old_x, x) = (-9, 23), (old_y, y) = (47, -120)
此时因r=0，得最终结果gcd(240, 46)=2，x=-9，y=47

2. 二进制GCD算法变种

二进制GCD算法有以下演进时间线：

1961年: 原始二进制GCD概念出现
1967年: Josef Stein正式发表算法
1970年代: Knuth在TAOCP中分析和优化
1980-90年代: 各种优化变种出现，包括这个delta版本
2000年代: 被广泛用于密码学库和大数运算

接下来重点分析带有delta状态变量的版本，算法如下：

 1 def gcd(f, g):
 2     """Compute the GCD of an odd integer f and another integer g."""
 3     assert f & 1  # require f to be odd
 4     delta = 1     # additional state variable
 5     while g != 0:
 6         assert f & 1  # f will be odd in every iteration
 7         if delta > 0 and g & 1:
 8             delta, f, g = 1 - delta, g, (g - f) // 2
 9         elif g & 1:
10             delta, f, g = 1 + delta, f, (g + f) // 2
11         else:
12             delta, f, g = 1 + delta, f, (g    ) // 2
13     return abs(f)

该算法要求第一个参数f必须是奇数（第3行），并引入了状态变量delta，用于指导算法选择不同的约减策略，避免陷入低效循环。该算法证明分两部分：

1）先证明算法保持 gcd 不变（正确性不破坏）；

2）然后给出一个势函数（potential），并用它证明在每次若干步内势函数会严格下降，从而不可能无限迭代------也就保证终止（收敛）。同时指出 delta 在防止振荡 / 保证下降中的关键作用。

第1部分结论很容易得出，在结合f，g奇偶情况下gcd(g, (g - f)//2)，gcd(f, (g + f)//2)，gcd(f, g//2)这三种情况显然和gcd(f, g)是一样的。第2部分的证明比较复杂，涉及到势函数相关理论，知识盲区，请自行查阅相关资料，这里不再详细说明。

总之，相比如下未引入delta的算法一（在某些情况下会不收敛），上述算法是能保证收敛的。

def gcd_no_delta(f, g):
    assert f & 1
    while g != 0:
        assert f & 1
        if g & 1:
            g = (g - f) // 2
        else:
            g = g // 2
    return abs(f)

gcd_no_delta

另外相比，如下未引入delta的算法二，f，g直接判断属于"输入依赖型分支"，不同输入会导致不同的分支走向，容易在硬件层面产生 "分支预测错误"（尤其在加密算法中，输入的随机性会放大这种问题）。而delta引入后，分支判断虽然存在，但更多依赖内部状态变量 delta 的符号（delta > 0 或 delta ≤ 0），而非输入 f 和 g 的直接比较，delta 的更新规则是固定的（1 - delta 或 1 + delta），其变化模式相对可预测，降低了对输入随机性的敏感度，更适合常数时间实现（密码学算法的关键要求）。尤其在大数运算情况下，a > b 这类比较操作需要完整的减法和符号判断（硬件层面是减法器 + 符号位检测），而delta的状态更新（1 - delta 或 1 + delta）是简单的算术操作（本质是 delta 在0和1之间交替，或递增递减），计算成本更低。

def bad_gcd(f, g):
    n = 1
    while g != 0:
        if g & 1:  # g为奇数
            if f > g:
                f, g = g, (f - g) // 2  # 总是用f-g
            else:
                f, g = g, (g - f) // 2
        else:  # g为偶数
            f, g = f, g // 2
        print("{}: {} {}".format(n, f, g))
        n += 1
    return f

bad_gcd

3. 由GCD求模逆

对于质数M（大于2）来说求x（0<x<M）的模逆，因为M是质数所以gcd(M, x)=1，则存在a*x + b*M = 1，即a*x = 1 mod M，所以结合以上1和2小节的内容，可以由在gcd算法求解过程中求得x系数a，以下是详细算法：

def div2(M, x):
    """Helper routine to compute x/2 mod M (where M is odd)."""
    assert M & 1
    if x & 1: # If x is odd, make it even by adding M.
        x += M
    # x must be even now, so a clean division by 2 is possible.
    return x // 2

def modinv(M, x):
    """Compute the inverse of x mod M (given that it exists, and M is odd)."""
    assert M & 1
    delta, f, g, d, e = 1, M, x, 0, 1
    while g != 0:
        # Note that while division by two for f and g is only ever done on even inputs, this is
        # not true for d and e, so we need the div2 helper function.
        if delta > 0 and g & 1:
            delta, f, g, d, e = 1 - delta, g, (g - f) // 2, e, div2(M, e - d)
        elif g & 1:
            delta, f, g, d, e = 1 + delta, f, (g + f) // 2, d, div2(M, e + d)
        else:
            delta, f, g, d, e = 1 + delta, f, (g    ) // 2, d, div2(M, e    )
        # Verify that the invariants d=f/x mod M, e=g/x mod M are maintained.
        assert f % M == (d * x) % M
        assert g % M == (e * x) % M
    assert f == 1 or f == -1  # |f| is the GCD, it must be 1
    # Because of invariant d = f/x (mod M), 1/x = d/f (mod M). As |f|=1, d/f = d*f.
    return (d * f) % M

该算法基于二进制扩展GCD算法，通过不断将问题规模减半来高效计算模逆元，首先明确算法以下关键变量：

• M: 模数（必须是奇数）

• x: 要求逆元的数

• f, g: 跟踪GCD计算的两个值

• d, e: 跟踪系数，维护关键不变量

• delta: 控制算法分支的状态变量

算法关键在于每次迭代都维护了以下等式λ：

f ≡ d * x (mod M)
g ≡ e * x (mod M)

这意味着每次迭代d和e始终是f和g在模M下关于x的系数，这样只要保证初始时等式成立，以及每次迭代更新f，g时，按计算规则得到的d，e和f，g仍满足以上等式，这就能保证到最后求得最大公约数1时，以上等式仍成立，及找出了最终的逆元d。

以循环迭代中第1种情况为例进行分析，根据规则更新后的f' = g，g' = (g - f)//2，也就是将g替换为新的f，将(g-f)//2替换为新的g，那么对应的系数更新规则必须保证：

由于更新后f' = g，由最一开始的等式g ≡ e * x (mod M)，可知要保证f' ≡ d' * x (mod M)成立，取d' = e即可，这正是算法中更新d的逻辑。算法中g的更新逻辑是g' = (g - f)//2，将初始等式λ代入更新逻辑得：

这就要求更新后的e'满足：

等价于：

而while迭代中第1种情况中的e的更新函数div2正是实现了该逻辑，在函数中由于输入e-d可能为奇数，此时需要加上奇数M（在模M下不影响最终结果）使得和为偶数再除于2。

同理可以分析while迭代中的另外两个分支，最终当算法终止时，有gcd(M, x) = |f| = 1，则当f = 1时，由f≡d*x≡1 mod M可知，d即为x逆元；当f = -1时，由d*x≡-1 mod M可知-d即为x逆元，正是算法返回值。

4. 模逆算法进一步优化

上述每次divstep迭代可以表示为矩阵乘法，对向量[f g]和[d e]应用如下的转换矩阵（1/2*t）：

其中根据迭代中分支的不同，(u, v, q, r)分别有不同的取值(0, 2, -1, 1)，(2, 0, 1, 1)，(2, 0, 0, 1)，在while每次迭代中都会用转换矩阵乘于相应的向量，而在转换矩阵中又包含除于2的操作，这样整个while循环会包含除于2^N的操作，对于f和g来说算法已经保证了每次迭代的除法可以通过移位来实现，而对于d和e来说，这些个除法是非常费时的操作，所以可以在每次迭代的矩阵乘法时不执行除于2的操作，而把该除法操作留到最后步骤执行除于2^N操作，由此得到以下函数：

def divsteps_n_matrix(delta, f, g):
    """Compute delta and transition matrix t after N divsteps (multiplied by 2^N)."""
    u, v, q, r = 1, 0, 0, 1 # start with identity matrix
    for _ in range(N):
        if delta > 0 and g & 1:
            delta, f, g, u, v, q, r = 1 - delta, g, (g - f) // 2, 2*q, 2*r, q-u, r-v
        elif g & 1:
            delta, f, g, u, v, q, r = 1 + delta, f, (g + f) // 2, 2*u, 2*v, q+u, r+v
        else:
            delta, f, g, u, v, q, r = 1 + delta, f, (g    ) // 2, 2*u, 2*v, q  , r
    return delta, (u, v, q, r)

后续还需进行如下计算：

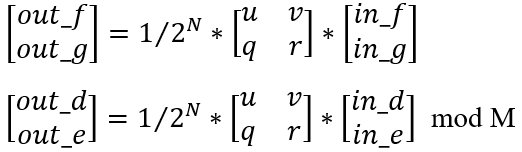
由推导过程可知，最后u，v，q，r组成的矩阵乘于初始向量[f g]以后得出的向量每个元素都是2^N的倍数（可由初始值实际验算下），所以有以下的更新函数：

def update_fg(f, g, t):
    """Multiply matrix t/2^N with [f, g]."""
    u, v, q, r = t
    cf, cg = u*f + v*g, q*f + r*g
    # (t / 2^N) should cleanly apply to [f,g] so the result of t*[f,g] should have N zero
    # bottom bits.
    assert cf % 2**N == 0
    assert cg % 2**N == 0
    return cf >> N, cg >> N

对于d和e来说上述结论并不成立，这里需要一个和div2函数类似的在模M下除于2^N的函数，借助该函数可实现d，e的更新：

def div2n(M, Mi, x):
    """Compute x/2^N mod M, given Mi = 1/M mod 2^N."""
    assert (M * Mi) % 2**N == 1
    # Find a factor m such that m*M has the same bottom N bits as x. We want:
    #     (m * M) mod 2^N = x mod 2^N
    # <=> m mod 2^N = (x / M) mod 2^N
    # <=> m mod 2^N = (x * Mi) mod 2^N
    m = (Mi * x) % 2**N
    # Subtract that multiple from x, cancelling its bottom N bits.
    x -= m * M
    # Now a clean division by 2^N is possible.
    assert x % 2**N == 0
    return (x >> N) % M

def update_de(d, e, t, M, Mi):
    """Multiply matrix t/2^N with [d, e], modulo M."""
    u, v, q, r = t
    cd, ce = u*d + v*e, q*d + r*e
    return div2n(M, Mi, cd), div2n(M, Mi, ce)

综合上述所有，即可给出执行N divsteps版本的modinv函数：

def modinv(M, Mi, x):
    """Compute the modular inverse of x mod M, given Mi=1/M mod 2^N."""
    assert M & 1
    delta, f, g, d, e = 1, M, x, 0, 1
    while g != 0:
        # Compute the delta and transition matrix t for the next N divsteps (this only needs
        # (N+1)-bit signed integer arithmetic).
        delta, t = divsteps_n_matrix(delta, f % 2**N, g % 2**N)
        # Apply the transition matrix t to [f, g]:
        f, g = update_fg(f, g, t)
        # Apply the transition matrix t to [d, e]:
        d, e = update_de(d, e, t, M, Mi)
    return (d * f) % M

这意味着在实践中，我们将始终执行多个N个div步骤。这不是问题，因为一旦g=0，进一步的divsteps就不再影响f、g、d或e（只有δ继续增加），这就能保证不管输入是何止，算法运行步骤一致，从而保证了算法时间一致性。

3.3 secp256k1_modinv32源码分析

结合上述内容分析下模逆的核心函数secp256k1_modinv32，其源码如下：

 1 /* Compute the inverse of x modulo modinfo->modulus, and replace x with it (constant time in x). */
 2 static void secp256k1_modinv32(secp256k1_modinv32_signed30 *x, const secp256k1_modinv32_modinfo *modinfo) {
 3     /* Start with d=0, e=1, f=modulus, g=x, zeta=-1. */
 4     secp256k1_modinv32_signed30 d = {{0}};
 5     secp256k1_modinv32_signed30 e = {{1}};
 6     secp256k1_modinv32_signed30 f = modinfo->modulus;
 7     secp256k1_modinv32_signed30 g = *x;
 8     int i;
 9     int32_t zeta = -1; /* zeta = -(delta+1/2); delta is initially 1/2. */
10 
11     /* Do 20 iterations of 30 divsteps each = 600 divsteps. 590 suffices for 256-bit inputs. */
12     for (i = 0; i < 20; ++i) {
13         /* Compute transition matrix and new zeta after 30 divsteps. */
14         secp256k1_modinv32_trans2x2 t;
15         zeta = secp256k1_modinv32_divsteps_30(zeta, f.v[0], g.v[0], &t);
16         /* Update d,e using that transition matrix. */
17         secp256k1_modinv32_update_de_30(&d, &e, &t, modinfo);
18         /* Update f,g using that transition matrix. */
19         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&f, 9, &modinfo->modulus, -1) > 0); /* f > -modulus */
20         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&f, 9, &modinfo->modulus, 1) <= 0); /* f <= modulus */
21         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&g, 9, &modinfo->modulus, -1) > 0); /* g > -modulus */
22         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&g, 9, &modinfo->modulus, 1) < 0);  /* g <  modulus */
23 
24         secp256k1_modinv32_update_fg_30(&f, &g, &t);
25 
26         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&f, 9, &modinfo->modulus, -1) > 0); /* f > -modulus */
27         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&f, 9, &modinfo->modulus, 1) <= 0); /* f <= modulus */
28         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&g, 9, &modinfo->modulus, -1) > 0); /* g > -modulus */
29         VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&g, 9, &modinfo->modulus, 1) < 0);  /* g <  modulus */
30     }
31 
32     /* At this point sufficient iterations have been performed that g must have reached 0
33      * and (if g was not originally 0) f must now equal +/- GCD of the initial f, g
34      * values i.e. +/- 1, and d now contains +/- the modular inverse. */
35 
36     /* g == 0 */
37     VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&g, 9, &SECP256K1_SIGNED30_ONE, 0) == 0);
38     /* |f| == 1, or (x == 0 and d == 0 and f == modulus) */
39     VERIFY_CHECK(secp256k1_modinv32_mul_cmp_30(&f, 9, &SECP256K1_SIGNED30_ONE, -1) == 0 ||
40                  secp256k1_modinv32_mul_cmp_30(&f, 9, &SECP256K1_SIGNED30_ONE, 1) == 0 ||
41                  (secp256k1_modinv32_mul_cmp_30(x, 9, &SECP256K1_SIGNED30_ONE, 0) == 0 &&
42                   secp256k1_modinv32_mul_cmp_30(&d, 9, &SECP256K1_SIGNED30_ONE, 0) == 0 &&
43                   secp256k1_modinv32_mul_cmp_30(&f, 9, &modinfo->modulus, 1) == 0));
44 
45     /* Optionally negate d, normalize to [0,modulus), and return it. */
46     secp256k1_modinv32_normalize_30(&d, f.v[8], modinfo);
47     *x = d;
48 }

函数整体流程和上一节的介绍基本一致，不再进行详细分析，这里重点分析下函数中容易让人困惑的几个点。

1. 参数zeta

在代码一开始引入映射zeta = -(delta+1/2)，则在delta取值1/2时，zeta取值为-1，以此为起点进行迭代，在zeta引入后，有以下迭代分支：

zeta<0 且 g&1：zeta=-zeta-2，对应之前delta>0且g&1分支；

(zeta>=0 且 g&1)或g为偶数：zeta=zeta-1，对应之前delta另外另种分支；

这样进行精心设计的好处是能用能用移位异或等操作完全替换比较操作（在密码学领域，消除分支判断，实现运行恒定时间）。

/* Compute the transition matrix and zeta for 30 divsteps.
 *
 * Input:  zeta: initial zeta
 *         f0:   bottom limb of initial f
 *         g0:   bottom limb of initial g
 * Output: t: transition matrix
 * Return: final zeta
 *
 * Implements the divsteps_n_matrix function from the explanation.
 */
static int32_t secp256k1_modinv32_divsteps_30(int32_t zeta, uint32_t f0, uint32_t g0, secp256k1_modinv32_trans2x2 *t) {
    /* u,v,q,r are the elements of the transformation matrix being built up,
     * starting with the identity matrix. Semantically they are signed integers
     * in range [-2^30,2^30], but here represented as unsigned mod 2^32. This
     * permits left shifting (which is UB for negative numbers). The range
     * being inside [-2^31,2^31) means that casting to signed works correctly.
     */
    uint32_t u = 1, v = 0, q = 0, r = 1;
    volatile uint32_t c1, c2;
    uint32_t mask1, mask2, f = f0, g = g0, x, y, z;
    int i;

    for (i = 0; i < 30; ++i) {
        VERIFY_CHECK((f & 1) == 1); /* f must always be odd */
        VERIFY_CHECK((u * f0 + v * g0) == f << i);
        VERIFY_CHECK((q * f0 + r * g0) == g << i);
        /* Compute conditional masks for (zeta < 0) and for (g & 1). */
        c1 = zeta >> 31;
        mask1 = c1;
        c2 = g & 1;
        mask2 = -c2;
        /* Compute x,y,z, conditionally negated versions of f,u,v. */
        x = (f ^ mask1) - mask1;
        y = (u ^ mask1) - mask1;
        z = (v ^ mask1) - mask1;
        /* Conditionally add x,y,z to g,q,r. */
        g += x & mask2;
        q += y & mask2;
        r += z & mask2;
        /* In what follows, mask1 is a condition mask for (zeta < 0) and (g & 1). */
        mask1 &= mask2;
        /* Conditionally change zeta into -zeta-2 or zeta-1. */
        zeta = (zeta ^ mask1) - 1;
        /* Conditionally add g,q,r to f,u,v. */
        f += g & mask1;
        u += q & mask1;
        v += r & mask1;
        /* Shifts */
        g >>= 1;
        u <<= 1;
        v <<= 1;
        /* Bounds on zeta that follow from the bounds on iteration count (max 20*30 divsteps). */
        VERIFY_CHECK(zeta >= -601 && zeta <= 601);
    }
    /* Return data in t and return value. */
    t->u = (int32_t)u;
    t->v = (int32_t)v;
    t->q = (int32_t)q;
    t->r = (int32_t)r;
    /* The determinant of t must be a power of two. This guarantees that multiplication with t
     * does not change the gcd of f and g, apart from adding a power-of-2 factor to it (which
     * will be divided out again). As each divstep's individual matrix has determinant 2, the
     * aggregate of 30 of them will have determinant 2^30. */
    VERIFY_CHECK((int64_t)t->u * t->r - (int64_t)t->v * t->q == ((int64_t)1) << 30);
    return zeta;
}

secp256k1_modinv32_divsteps_30

代码中zeta核心更新逻辑如下：

1 /* Compute conditional masks for (zeta < 0) and for (g & 1). */
2 c1 = zeta >> 31;
3 mask1 = c1;
4 c2 = g & 1;
5 mask2 = -c2;
6 mask1 &= mask2;
7 /* Conditionally change zeta into -zeta-2 or zeta-1. */
8 zeta = (zeta ^ mask1) - 1;

第2行处代码用于获取zeta符号，当zeta为非负数时c1=0，当zeta为负数时c1=0xFFFFFFFF，所以对于mask1来说，要么取值为0，要么为0xFFFFFFFF。第3行当g为奇数时，c2=1，对应mask2为0xFFFFFFFF，当g为偶数时，c2=0，对应mask2为0。第6行表明当g 奇数 且 zeta < 0时，mask1取值为0xFFFFFFFF，这时，第8行zeta=(zeta ^ -1) - 1 = (~zeta) - 1 = -zeta -1 - 1 = -zeta-2，即对应之前说的分支1；而其他情况下zeta = zeta -1。

2. 迭代次数

在Bernstein--Yang的论文 "Fast constant-time gcd computation and modular inversion" 中给出：

对于n位整数输入，需要的最大divsteps数量大约是2n+C，其中C是一个很小的常数。另外文中也说了在<=1.45n divsteps已经足够保证收敛，但是现实里通常会再留安全裕度。

在secp256k1的实现里：选择600 divsteps作为固定上限（方便分组，且有足够裕度），实际是只需要590 divsteps就能保证覆盖256位输入的最坏情况，这里590的数字来自对 safegcd 算法的 worst-case 分析（参考 secp256k1 开发者文档和论文中的 bound），即在 256 位范围内，任意输入的 GCD 计算最多 590 步就一定能结束。在库实现中，最终进行了20x30分组，这样的好处是：

• 批处理 (batching)：每次不做 1 个 divstep，而是"打包"多个（这里是 30 个），用矩阵乘法批量更新系数，这样减少分支、提高效率。

• 20 组 × 30 步 = 600 步：实现里用固定循环展开，保证 constant-time（无论输入是什么，都走一样的循环次数）。

所以这两个数字（30 和 20）并不是数学限制，而是工程上选择的「批大小」和「循环次数」。

参考：

1. https://cocalc.com/github/dogecoin/dogecoin/blob/master/src/secp256k1/doc/safegcd_implementation.md

2. https://blog.csdn.net/m0_74707185/article/details/147030492

3. https://cocalc.com/github/dogecoin/dogecoin/blob/master/src/secp256k1/src/modinv32_impl.h