SymPy 绘图完全指南：从基础到高级应用

SymPy 是一个强大的符号数学 Python 库，它不仅能够进行符号计算，还提供了基于 Matplotlib 的绘图功能。本文将全面介绍如何使用 SymPy 进行各种数学绘图，每个示例都是完整且独立的代码块。

基础二维函数绘图

让我们从最基本的二维函数绘图开始，这是 SymPy 绘图功能的核心：

python 复制代码

import sympy as sp
x = sp.symbols('x')

# 基本二次函数绘图
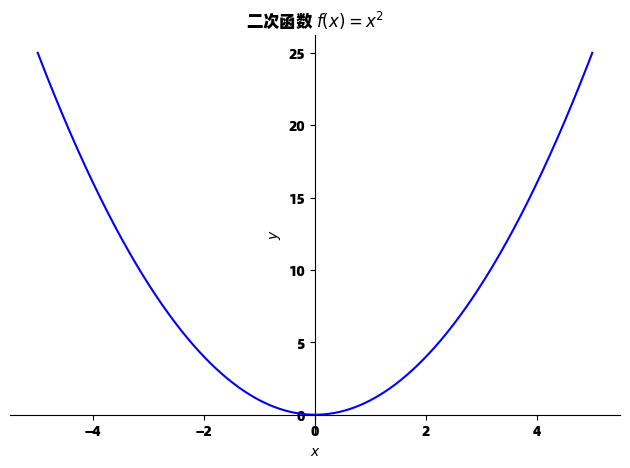
p = sp.plot(x**2, (x, -5, 5), 
           title="二次函数 $f(x) = x^2$",
           xlabel="$x$", 
           ylabel="$y$",
           line_color='blue')
p.show()

这段代码绘制了一个简单的二次函数 f(x)=x2f(x) = x^2f(x)=x2，展示了 SymPy 绘图的基本语法：定义符号变量、指定函数表达式、设置绘图区间，并添加必要的标签和标题。

多函数比较绘图

在实际应用中，我们经常需要比较多个函数的特性：

python 复制代码

import sympy as sp
x = sp.symbols('x')

# 比较不同幂次的函数
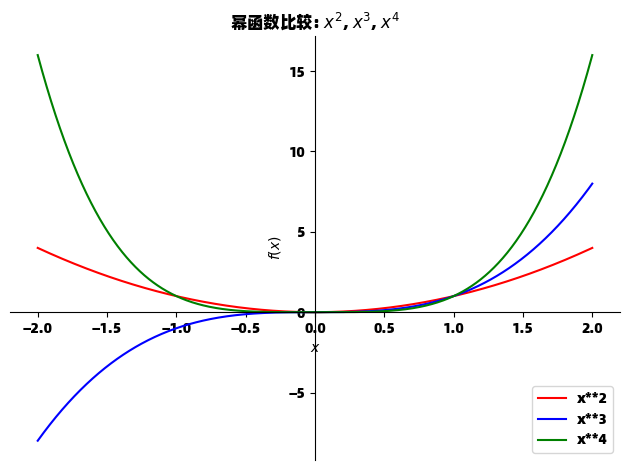
p = sp.plot(x**2, x**3, x**4, (x, -2, 2),
           title="幂函数比较: $x^2$, $x^3$, $x^4$",
           legend=True,
           show=False)

# 自定义线条颜色和样式
p[0].line_color = 'red'
p[1].line_color = 'blue' 
p[2].line_color = 'green'
p.show()

这个例子展示了如何在同一坐标系中绘制多个函数，并使用图例和不同颜色区分它们。这在分析函数性质时非常有用。

参数方程绘图

参数方程能够描述许多用显函数难以表达的曲线：

python 复制代码

import sympy as sp
t = sp.symbols('t')

# 绘制参数方程 - 椭圆
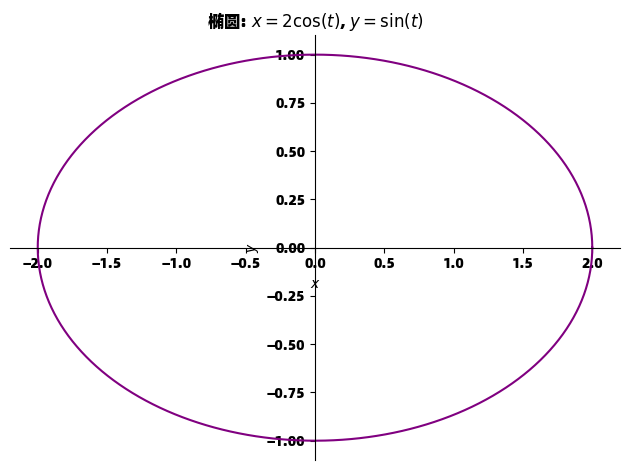
p = sp.plotting.plot_parametric(2*sp.cos(t), sp.sin(t), (t, 0, 2*sp.pi),
                               title="椭圆: $x=2\\cos(t)$, $y=\\sin(t)$",
                               xlabel="$x$",
                               ylabel="$y$",
                               line_color='purple')
p.show()

参数方程绘图特别适合描述闭合曲线、螺旋线和其他复杂轨迹。这里我们绘制了一个椭圆，其参数方程为 x=2cos⁡(t)x=2\cos(t)x=2cos(t), y=sin⁡(t)y=\sin(t)y=sin(t)。

极坐标绘图

虽然 SymPy 没有专门的极坐标绘图函数，但我们可以通过参数方程模拟极坐标效果：

python 复制代码

import sympy as sp
t = sp.symbols('t')

# 通过参数方程实现极坐标绘图 - 三叶玫瑰线
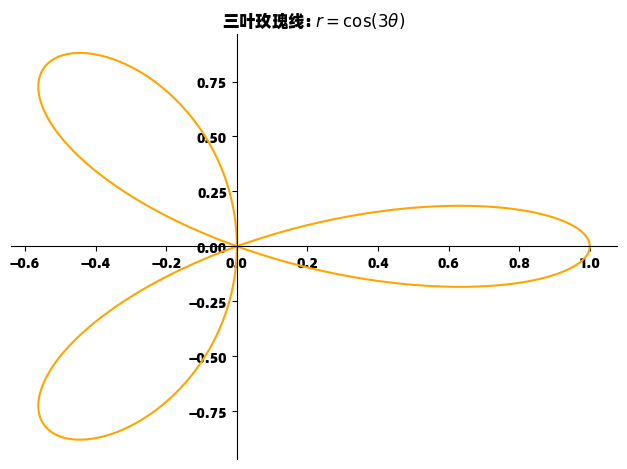
p = sp.plotting.plot_parametric(sp.cos(3*t)*sp.cos(t), 
                               sp.cos(3*t)*sp.sin(t), 
                               (t, 0, sp.pi),
                               title="三叶玫瑰线: $r=\\cos(3\\theta)$",
                               line_color='orange')
p.show()

这个例子展示了如何用参数方程绘制极坐标函数 r=cos⁡(3θ)r=\cos(3\theta)r=cos(3θ)，即著名的三叶玫瑰线。

三维函数曲面绘图

SymPy 能够绘制令人印象深刻的三维函数曲面：

python 复制代码

import sympy as sp
x, y = sp.symbols('x y')

# 三维曲面绘图
p = sp.plotting.plot3d(sp.sin(sp.sqrt(x**2 + y**2)), 
                      (x, -10, 10), (y, -10, 10),
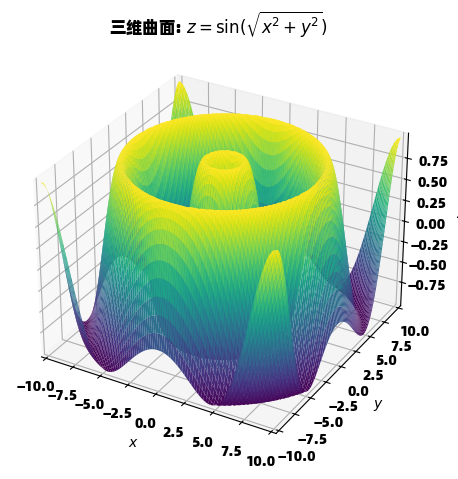
                      title="三维曲面: $z=\\sin(\\sqrt{x^2 + y^2})$",
                      xlabel="$x$",
                      ylabel="$y$",
                      zlabel="$z$")
p.show()

这个波纹曲面 z=sin⁡(x2+y2)z=\sin(\sqrt{x^2 + y^2})z=sin(x2+y2 ) 展示了 SymPy 处理三维函数的能力。三维绘图在可视化多元函数时极为有用。

三维参数曲面

对于更复杂的三维形状，参数曲面是最佳选择：

python 复制代码

import sympy as sp
from sympy.plotting import plot3d_parametric_surface
u, v = sp.symbols('u v')

# 绘制环面
p = plot3d_parametric_surface((2 + sp.cos(u))*sp.cos(v),
                             (2 + sp.cos(u))*sp.sin(v),
                             sp.sin(u),
                             (u, 0, 2*sp.pi), (v, 0, 2*sp.pi),
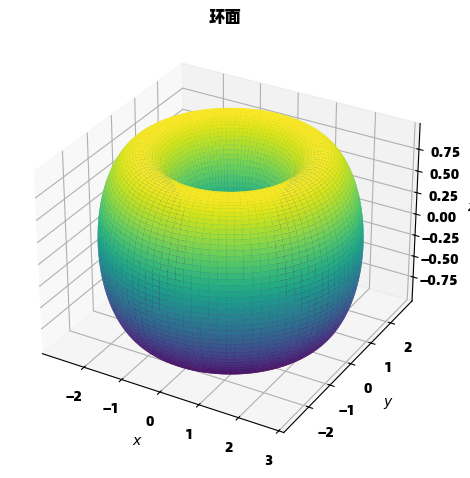
                             title="环面",
                             xlabel="$x$",
                             ylabel="$y$", 
                             zlabel="$z$")
p.show()

环面是一个经典的参数曲面例子，其参数方程清晰地描述了这一复杂三维形状的几何结构。

隐函数绘图

隐函数绘图能够可视化那些无法显式表示为 y=f(x)y=f(x)y=f(x) 的曲线：

python 复制代码

import sympy as sp
from sympy.plotting import plot_implicit
x, y = sp.symbols('x y')

# 绘制卡西尼卵形线
p = plot_implicit((x**2 + y**2)**2 - 2*(x**2 - y**2) - 1, 
                 (x, -2, 2), (y, -2, 2),
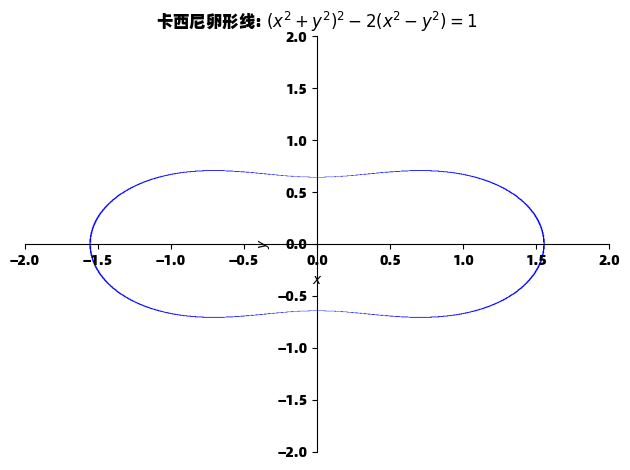
                 title="卡西尼卵形线: $(x^2 + y^2)^2 - 2(x^2 - y^2) = 1$")
p.show()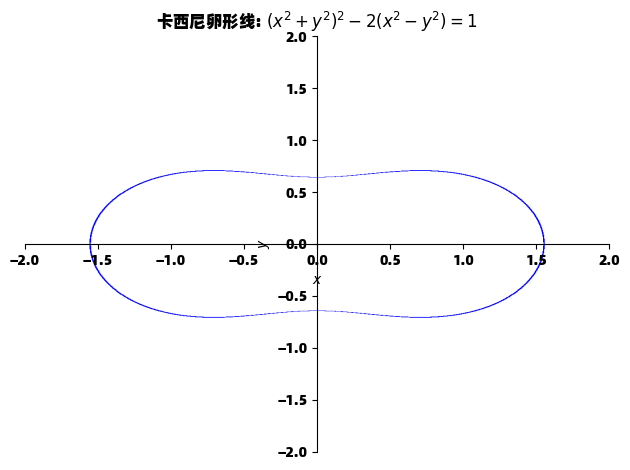

隐函数绘图对于研究代数曲线特别有用，如这里的卡西尼卵形线，它由方程 (x2+y2)2−2(x2−y2)=1(x^2 + y^2)^2 - 2(x^2 - y^2) = 1(x2+y2)2−2(x2−y2)=1 定义。

分段函数绘图

许多实际问题的数学模型需要分段函数来描述：

python 复制代码

import sympy as sp
x = sp.symbols('x')

# 定义并绘制分段函数
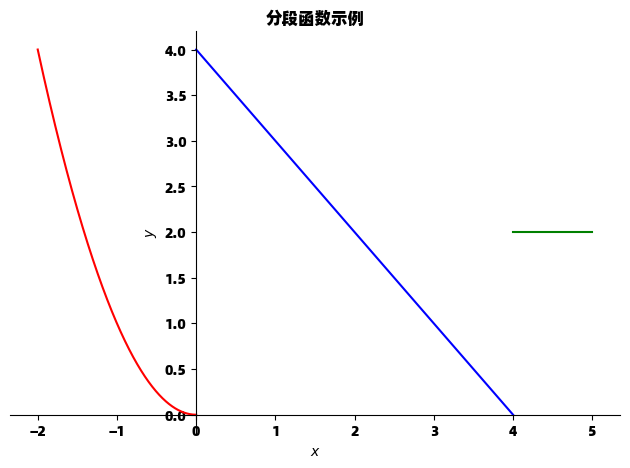
p1 = sp.plot(x**2, (x, -2, 0), line_color='red', show=False)
p2 = sp.plot(4 - x, (x, 0, 4), line_color='blue', show=False)
p3 = sp.plot(2, (x, 4, 5), line_color='green', show=False)

# 合并所有分段
p1.extend(p2)
p1.extend(p3)
p1.title = "分段函数示例"
p1.xlabel = "$x$"
p1.ylabel = "$y$"
p1.show()

分段函数绘图通过分别绘制每个区间然后合并的方式实现，这种方法虽然稍显繁琐，但能够准确表示复杂的分段定义。

处理有渐近线的函数

有渐近线的函数需要特殊处理，因为直接绘制会导致数值不稳定：

python 复制代码

import sympy as sp
x = sp.symbols('x')

# 分别绘制正负区间以避免渐近线问题
p_left = sp.plot(1/x, (x, -3, -0.1), line_color='blue', show=False)
p_right = sp.plot(1/x, (x, 0.1, 3), line_color='blue', show=False)

# 合并图像
p_left.extend(p_right)
p_left.title = "函数 $f(x) = \\frac{1}{x}$ 及其渐近线"
p_left.xlabel = "$x$"
p_left.ylabel = "$y$"
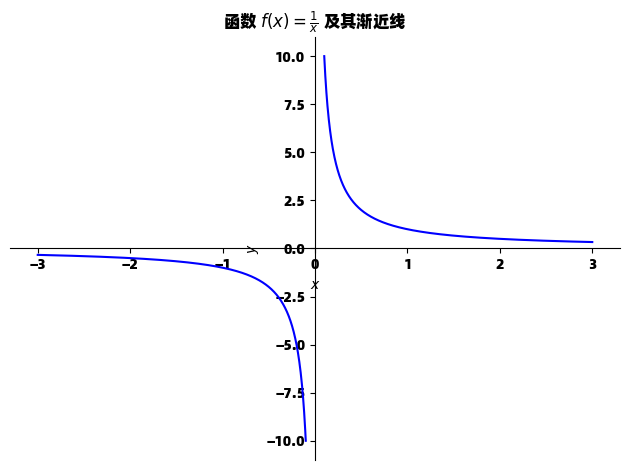
p_left.show()

对于像 f(x)=1xf(x) = \frac{1}{x}f(x)=x1 这样在 x=0x=0x=0 处有垂直渐近线的函数，我们需要避开不连续点，分别绘制左右两侧的区间。

复杂函数组合分析

通过组合不同类型的函数，我们可以分析它们的相互作用：

python 复制代码

import sympy as sp
x = sp.symbols('x')

# 绘制三角函数组合
p = sp.plot(sp.sin(x), sp.cos(x), sp.sin(x)+sp.cos(x), 
           (x, -2*sp.pi, 2*sp.pi),
           title="三角函数组合: $\\sin(x)$, $\\cos(x)$, $\\sin(x)+\\cos(x)$",
           legend=True,
           show=False)

# 设置不同颜色
p[0].line_color = 'red'
p[1].line_color = 'blue'
p[2].line_color = 'green'
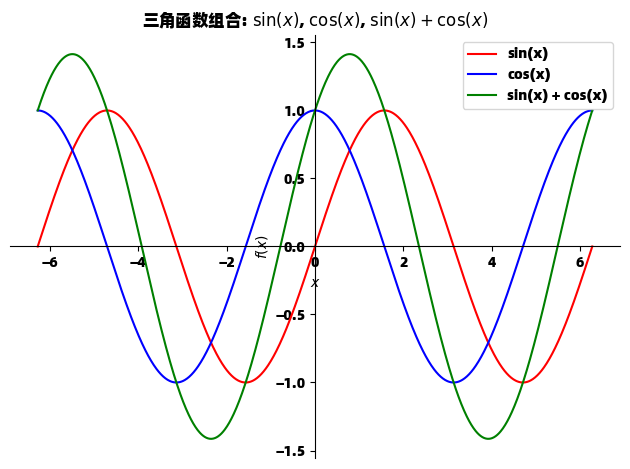
p.show()

这个例子展示了如何同时可视化正弦函数、余弦函数以及它们的和函数，通过颜色和图例清晰地区分各个曲线。

三维参数曲线

三维参数曲线用于描述空间中的轨迹：

python 复制代码

import sympy as sp
from sympy.plotting import plot3d_parametric_line
t = sp.symbols('t')

# 绘制螺旋线
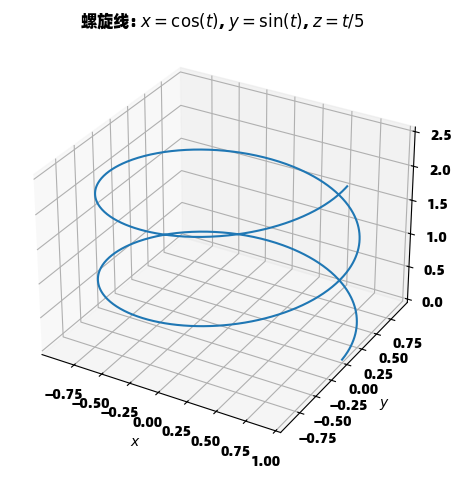
p = plot3d_parametric_line(sp.cos(t), sp.sin(t), t/5, 
                          (t, 0, 4*sp.pi),
                          title="螺旋线: $x=\\cos(t)$, $y=\\sin(t)$, $z=t/5$",
                          xlabel="$x$",
                          ylabel="$y$",
                          zlabel="$z$")
p.show()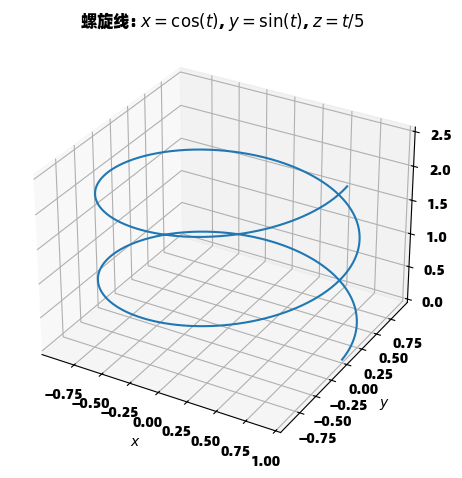

螺旋线是一个经典的三维参数曲线例子，其参数方程 x=cos⁡(t)x=\cos(t)x=cos(t), y=sin⁡(t)y=\sin(t)y=sin(t), z=t/5z=t/5z=t/5 清晰地描述了点在空间中的运动轨迹。

高级应用：自定义绘图样式

SymPy 绘图支持丰富的自定义选项，可以创建专业质量的数学图形：

python 复制代码

import sympy as sp
x = sp.symbols('x')

# 高级自定义绘图
p = sp.plot(sp.exp(-x**2/2)/sp.sqrt(2*sp.pi), (x, -4, 4),
           title="高斯函数: $\\frac{1}{\\sqrt{2\\pi}} e^{-\\frac{x^2}{2}}$",
           xlabel="$x$",
           ylabel="$f(x)$",
           line_color='darkred',
           line_width=2,
           legend=True,
           show=False)

# 进一步自定义坐标轴
p.xlim = (-4, 4)
p.ylim = (0, 0.5)
p.show()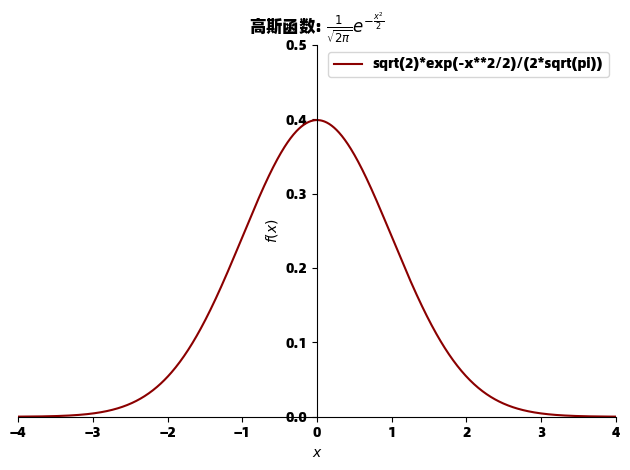

这个高斯函数绘图展示了如何通过自定义线条颜色、粗细和坐标轴范围来创建更具视觉吸引力的数学图形。

结语

SymPy 的绘图功能为数学可视化和教育提供了强大而灵活的工具。通过本文展示的各种示例，我们可以看到 SymPy 不仅能够处理基本的函数绘图，还能应对参数方程、隐函数、三维曲面和分段函数等复杂情况。虽然 SymPy 的绘图功能基于 Matplotlib，但其符号数学的特性使得数学表达式的输入更加直观自然。

无论是用于数学教学、科学研究还是工程应用，SymPy 绘图都是一个值得掌握的强大工具。通过结合 SymPy 的符号计算能力和可视化功能，我们能够更深入地理解和探索数学概念与关系。