树上倍增和LCA算法---上

little~钰2025-10-01 18:28

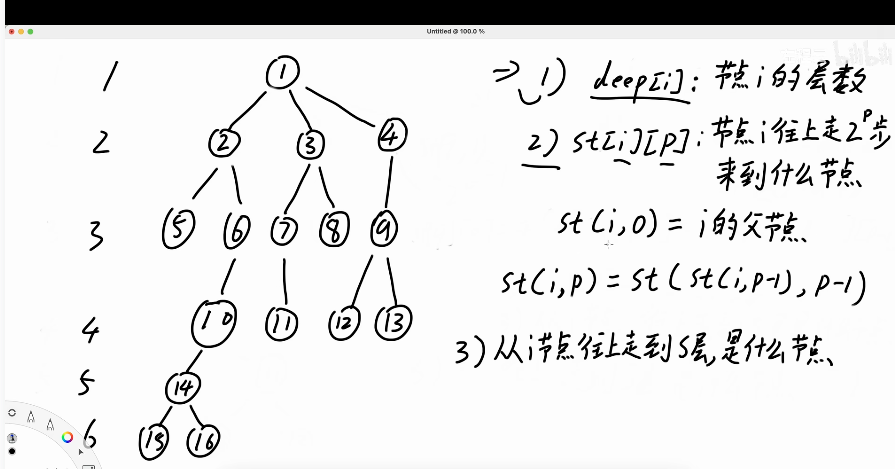
树上倍增： 建立deep和st数组，就可以求出从一个节点往上走s步来到的节点。比如求从16走3步来到的节点，16走3步来到第3层，首先枚举走4步(8步及更多的步数没必要枚举，因为16所在第6层都不足8步)，查st表来到2节点，在第2层，所以不要；然后走2步，到第4层的10，所以走到10节点；然后枚举走一步，来到第3层的6节点。

1483. 树节点的第 K 个祖先 - 力扣（LeetCode）

java 复制代码 
// 树节点的第K个祖先
// 树上有n个节点，编号0 ~ n-1，树的结构用parent数组代表
// 其中parent[i]是节点i的父节点，树的根节点是编号为0
// 树节点i的第k个祖先节点，是从节点i开始往上跳k步所来到的节点
// 实现TreeAncestor类
// TreeAncestor(int n, int[] parent) : 初始化
// getKthAncestor(int i, int k) : 返回节点i的第k个祖先节点，不存在返回-1
// 测试链接 : https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/
public class Code01_KthAncestor {

	class TreeAncestor {

		public static int MAXN = 50001;

		public static int LIMIT = 16;

		// 根据节点个数n，计算出2的几次方就够用了
		public static int power;

		public static int log2(int n) {
			int ans = 0;
			while ((1 << ans) <= (n >> 1)) {
				ans++;
			}
			return ans;
		}

		// 链式前向星建图
		public static int[] head = new int[MAXN];

		public static int[] next = new int[MAXN];

		public static int[] to = new int[MAXN];

		public static int cnt;

		// deep[i] : 节点i在第几层
		public static int[] deep = new int[MAXN];

		// stjump[i][p] : 节点i往上跳2的p次方步，到达的节点编号
		public static int[][] stjump = new int[MAXN][LIMIT];

		public TreeAncestor(int n, int[] parent) {
			power = log2(n);
			cnt = 1;
			Arrays.fill(head, 0, n, 0);
			for (int i = 1; i < parent.length; i++) {
				addEdge(parent[i], i);
			}
			dfs(0, 0);
		}

		public static void addEdge(int u, int v) {
			next[cnt] = head[u];
			to[cnt] = v;
			head[u] = cnt++;
		}

		// 当前来到i节点，i节点父亲节点是f
		public static void dfs(int i, int f) {
			if (i == 0) {
				deep[i] = 1;
			} else {
				deep[i] = deep[f] + 1;
			}
			stjump[i][0] = f;
			for (int p = 1; p <= power; p++) {//处理自己
				stjump[i][p] = stjump[stjump[i][p - 1]][p - 1];
			}
			for (int e = head[i]; e != 0; e = next[e]) {//处理孩子
				dfs(to[e], i);
			}
		}

		public int getKthAncestor(int i, int k) {
			if (deep[i] <= k) {
				return -1;
			}
			// s是想要去往的层数
			int s = deep[i] - k;
			for (int p = power; p >= 0; p--) {
				if (deep[stjump[i][p]] >= s) {
					i = stjump[i][p];
				}
			}
			return i;
		}

	}

}

树上倍增解决LCA问题：

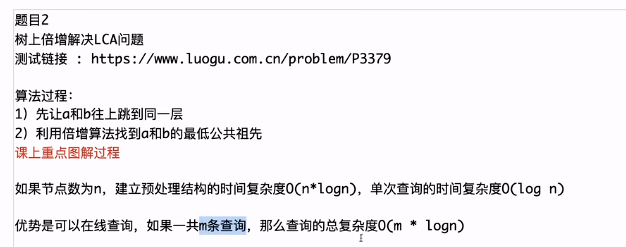
查询过程：比如要查询a和b的最近公共祖先，先让深度大的节点走到深度小的节点的深度，就是让a走到第37层，然后同时走64步，发现都到达-1这个节点，所以不要；然后走32步，到达第5层的同一个节点，不要；然后走16步，到达不一样的节点，所以要；以此类推，最后两个节点同时往上走一步就到达了他们的最近公共祖先

递归代码

P3379 【模板】最近公共祖先（LCA） - 洛谷

java 复制代码 
// 树上倍增解法
// 测试链接 : https://www.luogu.com.cn/problem/P3379
// 提交以下的code，提交时请把类名改成"Main"
// C++这么写能通过，java会因为递归层数太多而爆栈
// java能通过的写法参考本节课Code02_Multiply2文件

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code02_Multiply1 {

	public static int MAXN = 500001;

	public static int LIMIT = 20;

	// 根据节点个数n，计算出2的几次方就够用了
	public static int power;

	public static int log2(int n) {
		int ans = 0;
		while ((1 << ans) <= (n >> 1)) {
			ans++;
		}
		return ans;
	}

	// 链式前向星建图
	public static int[] head = new int[MAXN];

	public static int[] next = new int[MAXN << 1];

	public static int[] to = new int[MAXN << 1];

	public static int cnt;

	// deep[i] : 节点i在第几层
	public static int[] deep = new int[MAXN];

	// stjump[i][p] : 节点i往上跳2的p次方步，到达的节点编号
	public static int[][] stjump = new int[MAXN][LIMIT];

	public static void build(int n) {
		power = log2(n);
		cnt = 1;
		Arrays.fill(head, 1, n + 1, 0);
	}

	public static void addEdge(int u, int v) {
		next[cnt] = head[u];
		to[cnt] = v;
		head[u] = cnt++;
	}

	// dfs递归版
	// 一般来说都这么写，但是本题附加的测试数据很毒
	// java这么写就会因为递归太深而爆栈，c++这么写就能通过
	public static void dfs(int u, int f) {
		deep[u] = deep[f] + 1;
		stjump[u][0] = f;
		for (int p = 1; p <= power; p++) {
			stjump[u][p] = stjump[stjump[u][p - 1]][p - 1];
		}
		for (int e = head[u]; e != 0; e = next[e]) {
			if (to[e] != f) {
				dfs(to[e], u);
			}
		}
	}

	public static int lca(int a, int b) {
		if (deep[a] < deep[b]) {
			int tmp = a;
			a = b;
			b = tmp;
		}
		for (int p = power; p >= 0; p--) {
			if (deep[stjump[a][p]] >= deep[b]) {
				a = stjump[a][p];
			}
		}
		if (a == b) {
			return a;
		}
		for (int p = power; p >= 0; p--) {
			if (stjump[a][p] != stjump[b][p]) {
				a = stjump[a][p];
				b = stjump[b][p];
			}
		}
		return stjump[a][0];
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		in.nextToken();
		int n = (int) in.nval;
		in.nextToken();
		int m = (int) in.nval;
		in.nextToken();
		int root = (int) in.nval;
		build(n);
		for (int i = 1, u, v; i < n; i++) {
			in.nextToken();
			u = (int) in.nval;
			in.nextToken();
			v = (int) in.nval;
			addEdge(u, v);
			addEdge(v, u);
		}
		dfs(root, 0);
		for (int i = 1, a, b; i <= m; i++) {
			in.nextToken();
			a = (int) in.nval;
			in.nextToken();
			b = (int) in.nval;
			out.println(lca(a, b));
		}
		out.flush();
		out.close();
		br.close();
	}

}

迭代代码：

算法讲解118【扩展】树上问题专题1-树上倍增和LCA-上

java 复制代码 
// 树上倍增解法迭代版
// 测试链接 : https://www.luogu.com.cn/problem/P3379
// 所有递归函数一律改成等义的迭代版
// 提交以下的code，提交时请把类名改成"Main"，可以通过所有用例

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code02_Multiply2 {

	public static int MAXN = 500001;

	public static int LIMIT = 20;

	public static int power;

	public static int log2(int n) {
		int ans = 0;
		while ((1 << ans) <= (n >> 1)) {
			ans++;
		}
		return ans;
	}

	public static int cnt;

	public static int[] head = new int[MAXN];

	public static int[] next = new int[MAXN << 1];

	public static int[] to = new int[MAXN << 1];

	public static int[][] stjump = new int[MAXN][LIMIT];

	public static int[] deep = new int[MAXN];

	public static void build(int n) {
		power = log2(n);
		cnt = 1;
		Arrays.fill(head, 1, n + 1, 0);
	}

	public static void addEdge(int u, int v) {
		next[cnt] = head[u];
		to[cnt] = v;
		head[u] = cnt++;
	}

	// dfs迭代版
	// ufe是为了实现迭代版而准备的栈
	public static int[][] ufe = new int[MAXN][3];

	public static int stackSize, u, f, e;

	public static void push(int u, int f, int e) {
		ufe[stackSize][0] = u;
		ufe[stackSize][1] = f;
		ufe[stackSize][2] = e;
		stackSize++;
	}

	public static void pop() {
		--stackSize;
		u = ufe[stackSize][0];
		f = ufe[stackSize][1];
		e = ufe[stackSize][2];
	}

	public static void dfs(int root) {
		stackSize = 0;
		// 栈里存放三个信息
		// u : 当前处理的点
		// f : 当前点u的父节点
		// e : 处理到几号边了
		// 如果e==-1，表示之前没有处理过u的任何边
		// 如果e==0，表示u的边都已经处理完了
		push(root, 0, -1);
		while (stackSize > 0) {
			pop();
			if (e == -1) {
				deep[u] = deep[f] + 1;
				stjump[u][0] = f;
				for (int p = 1; p <= power; p++) {
					stjump[u][p] = stjump[stjump[u][p - 1]][p - 1];
				}
				e = head[u];
			} else {
				e = next[e];
			}
			if (e != 0) {
				push(u, f, e);
				if (to[e] != f) {
					push(to[e], u, -1);
				}
			}
		}
	}

	public static int lca(int a, int b) {
		if (deep[a] < deep[b]) {
			int tmp = a;
			a = b;
			b = tmp;
		}
		for (int p = power; p >= 0; p--) {
			if (deep[stjump[a][p]] >= deep[b]) {
				a = stjump[a][p];
			}
		}
		if (a == b) {
			return a;
		}
		for (int p = power; p >= 0; p--) {
			if (stjump[a][p] != stjump[b][p]) {
				a = stjump[a][p];
				b = stjump[b][p];
			}
		}
		return stjump[a][0];
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		in.nextToken();
		int n = (int) in.nval;
		in.nextToken();
		int m = (int) in.nval;
		in.nextToken();
		int root = (int) in.nval;
		build(n);
		for (int i = 1, u, v; i < n; i++) {
			in.nextToken();
			u = (int) in.nval;
			in.nextToken();
			v = (int) in.nval;
			addEdge(u, v);
			addEdge(v, u);
		}
		dfs(root);
		for (int i = 1, a, b; i <= m; i++) {
			in.nextToken();
			a = (int) in.nval;
			in.nextToken();
			b = (int) in.nval;
			out.println(lca(a, b));
		}
		out.flush();
		out.close();
		br.close();
	}

}
java 复制代码 
// tarjan算法解法
// 测试链接 : https://www.luogu.com.cn/problem/P3379
// 提交以下的code，提交时请把类名改成"Main"
// C++这么写能通过，java会因为递归层数太多而爆栈
// java能通过的写法参考本节课Code03_Tarjan2文件

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code03_Tarjan1 {

	public static int MAXN = 500001;

	// 链式前向星建图
	public static int[] headEdge = new int[MAXN];

	public static int[] edgeNext = new int[MAXN << 1];

	public static int[] edgeTo = new int[MAXN << 1];

	public static int tcnt;

	// 每个节点有哪些查询，也用链式前向星方式存储
	public static int[] headQuery = new int[MAXN];

	public static int[] queryNext = new int[MAXN << 1];

	public static int[] queryTo = new int[MAXN << 1];

	// 问题的编号，一旦有答案可以知道填写在哪
	public static int[] queryIndex = new int[MAXN << 1];

	public static int qcnt;

	// 某个节点是否访问过
	public static boolean[] visited = new boolean[MAXN];

	// 并查集
	public static int[] father = new int[MAXN];

	// 收集的答案
	public static int[] ans = new int[MAXN];

	public static void build(int n) {
		tcnt = qcnt = 1;
		Arrays.fill(headEdge, 1, n + 1, 0);
		Arrays.fill(headQuery, 1, n + 1, 0);
		Arrays.fill(visited, 1, n + 1, false);
		for (int i = 1; i <= n; i++) {
			father[i] = i;
		}
	}

	public static void addEdge(int u, int v) {
		edgeNext[tcnt] = headEdge[u];
		edgeTo[tcnt] = v;
		headEdge[u] = tcnt++;
	}

	public static void addQuery(int u, int v, int i) {
		queryNext[qcnt] = headQuery[u];
		queryTo[qcnt] = v;
		queryIndex[qcnt] = i;
		headQuery[u] = qcnt++;
	}

	// 并查集找头节点递归版
	// 一般来说都这么写，但是本题附加的测试数据很毒
	// java这么写就会因为递归太深而爆栈，C++这么写就能通过
	public static int find(int i) {
		if (i != father[i]) {
			father[i] = find(father[i]);
		}
		return father[i];
	}

	// tarjan算法递归版
	// 一般来说都这么写，但是本题附加的测试数据很毒
	// java这么写就会因为递归太深而爆栈，C++这么写就能通过
	public static void tarjan(int u, int f) {
		visited[u] = true;
		for (int e = headEdge[u], v; e != 0; e = edgeNext[e]) {
			v = edgeTo[e];
			if (v != f) {
				tarjan(v, u);
				father[v] = u;
			}
		}
		for (int e = headQuery[u], v; e != 0; e = queryNext[e]) {
			v = queryTo[e];
			if (visited[v]) {
				ans[queryIndex[e]] = find(v);
			}
		}
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		in.nextToken();
		int n = (int) in.nval;
		in.nextToken();
		int m = (int) in.nval;
		in.nextToken();
		int root = (int) in.nval;
		build(n);
		for (int i = 1, u, v; i < n; i++) {
			in.nextToken();
			u = (int) in.nval;
			in.nextToken();
			v = (int) in.nval;
			addEdge(u, v);
			addEdge(v, u);
		}
		for (int i = 1, u, v; i <= m; i++) {
			in.nextToken();
			u = (int) in.nval;
			in.nextToken();
			v = (int) in.nval;
			addQuery(u, v, i);
			addQuery(v, u, i);
		}
		tarjan(root, 0);
		for (int i = 1; i <= m; i++) {
			out.println(ans[i]);
		}
		out.flush();
		out.close();
		br.close();
	}

}
java 复制代码 
// tarjan算法解法迭代版
// 测试链接 : https://www.luogu.com.cn/problem/P3379
// 所有递归函数一律改成等义的迭代版
// 提交以下的code，提交时请把类名改成"Main"，可以通过所有用例

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;

public class Code03_Tarjan2 {

	public static int MAXN = 500001;

	public static int[] headEdge = new int[MAXN];

	public static int[] edgeNext = new int[MAXN << 1];

	public static int[] edgeTo = new int[MAXN << 1];

	public static int tcnt;

	public static int[] headQuery = new int[MAXN];

	public static int[] queryNext = new int[MAXN << 1];

	public static int[] queryTo = new int[MAXN << 1];

	public static int[] queryIndex = new int[MAXN << 1];

	public static int qcnt;

	public static boolean[] visited = new boolean[MAXN];

	public static int[] father = new int[MAXN];

	public static int[] ans = new int[MAXN];

	public static void build(int n) {
		tcnt = qcnt = 1;
		Arrays.fill(headEdge, 1, n + 1, 0);
		Arrays.fill(headQuery, 1, n + 1, 0);
		Arrays.fill(visited, 1, n + 1, false);
		for (int i = 1; i <= n; i++) {
			father[i] = i;
		}
	}

	public static void addEdge(int u, int v) {
		edgeNext[tcnt] = headEdge[u];
		edgeTo[tcnt] = v;
		headEdge[u] = tcnt++;
	}

	public static void addQuery(int u, int v, int i) {
		queryNext[qcnt] = headQuery[u];
		queryTo[qcnt] = v;
		queryIndex[qcnt] = i;
		headQuery[u] = qcnt++;
	}

	// 为了实现迭代版而准备的栈
	public static int[] stack = new int[MAXN];

	// 并查集找头节点迭代版
	public static int find(int i) {
		int size = 0;
		while (i != father[i]) {
			stack[size++] = i;
			i = father[i];
		}
		while (size > 0) {
			father[stack[--size]] = i;
		}
		return i;
	}

	// 为了实现迭代版而准备的栈
	public static int[][] ufe = new int[MAXN][3];

	public static int stackSize, u, f, e;

	public static void push(int u, int f, int e) {
		ufe[stackSize][0] = u;
		ufe[stackSize][1] = f;
		ufe[stackSize][2] = e;
		stackSize++;
	}

	public static void pop() {
		--stackSize;
		u = ufe[stackSize][0];
		f = ufe[stackSize][1];
		e = ufe[stackSize][2];
	}

	// 为了容易改成迭代版，修改一下递归版
	public static void tarjan(int u, int f) {
		visited[u] = true;
		for (int e = headEdge[u], v; e != 0; e = edgeNext[e]) {
			v = edgeTo[e];
			if (v != f) {
				tarjan(v, u);
				// 注意这里，注释了一行
//				father[v] = u;
			}
		}
		for (int e = headQuery[u], v; e != 0; e = queryNext[e]) {
			v = queryTo[e];
			if (visited[v]) {
				ans[queryIndex[e]] = find(v);
			}
		}
		// 注意这里，增加了一行
		father[u] = f;
	}

	// tarjan算法迭代版，根据上面的递归版改写
	public static void tarjan(int root) {
		stackSize = 0;
		// 栈里存放三个信息
		// u : 当前处理的点
		// f : 当前点u的父节点
		// e : 处理到几号边了
		// 如果e==-1，表示之前没有处理过u的任何边
		// 如果e==0，表示u的边都已经处理完了
		push(root, 0, -1);
		while (stackSize > 0) {
			pop();
			if (e == -1) {
				visited[u] = true;
				e = headEdge[u];
			} else {
				e = edgeNext[e];
			}
			if (e != 0) {
				push(u, f, e);
				if (edgeTo[e] != f) {
					push(edgeTo[e], u, -1);
				}
			} else {
				// e == 0代表u后续已经没有边需要处理了
				for (int q = headQuery[u], v; q != 0; q = queryNext[q]) {
					v = queryTo[q];
					if (visited[v]) {
						ans[queryIndex[q]] = find(v);
					}
				}
				father[u] = f;
			}
		}
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		in.nextToken();
		int n = (int) in.nval;
		in.nextToken();
		int m = (int) in.nval;
		in.nextToken();
		int root = (int) in.nval;
		build(n);
		for (int i = 1, u, v; i < n; i++) {
			in.nextToken();
			u = (int) in.nval;
			in.nextToken();
			v = (int) in.nval;
			addEdge(u, v);
			addEdge(v, u);
		}
		for (int i = 1, u, v; i <= m; i++) {
			in.nextToken();
			u = (int) in.nval;
			in.nextToken();
			v = (int) in.nval;
			addQuery(u, v, i);
			addQuery(v, u, i);
		}
		tarjan(root);
		for (int i = 1; i <= m; i++) {
			out.println(ans[i]);
		}
		out.flush();
		out.close();
		br.close();
	}

}
相关推荐
力扣蓝精灵2 小时前
今日分享 整数二分
算法
mc23562 小时前
5分钟学会微算法——Brian Kernighan 算法
算法
Excuse_lighttime2 小时前
除自身以外数组的乘积
java·数据结构·算法·leetcode·eclipse·动态规划
万添裁2 小时前
归并排序的三重境界
数据结构·算法
程序员三明治2 小时前
【重学数据结构】队列 Queue
数据结构·后端·算法
Coision.2 小时前
Linux C: 函数
java·c语言·算法
杜小暑2 小时前
数据结构之双向链表
c语言·数据结构·后端·算法·链表·动态内存管理
AndrewHZ3 小时前
【3D图像技术讨论】3A游戏场景重建实战指南：从数据采集到实时渲染的开源方案
人工智能·算法·游戏·3d·开源·llm·colmap
Juan_20123 小时前
P3051题解
c++·数学·算法·题解
热门推荐
01OpenSpeedy简介02GitHub 镜像站点03UV安装并设置国内源04在国行 macOS 下用 DeepSeek 补齐 Xcode 26 的 AI 能力：问题、原因与 mitmproxy 解决方案（含可用脚本与安装教程）05KGG转MP3工具|非KGM文件|解密音频06UV 工具安装与国内镜像源配置指南07阿里最新开源Wan2.2-Animate-14B 本地部署教程：统一双模态框架，MoE架构赋能电影级角色动画与替换08Linux下V2Ray安装配置指南09jdk21下载、安装（Windows、Linux、macOS）10Spec-Kit 使用指南