经典粒子群优化算法PSO-LSTM回归+SHAP分析+多输出+新数据预测!Matlab代码实现,主要用于多输入多输出的回归预测任务。以下是详细分析:
1. 主要功能
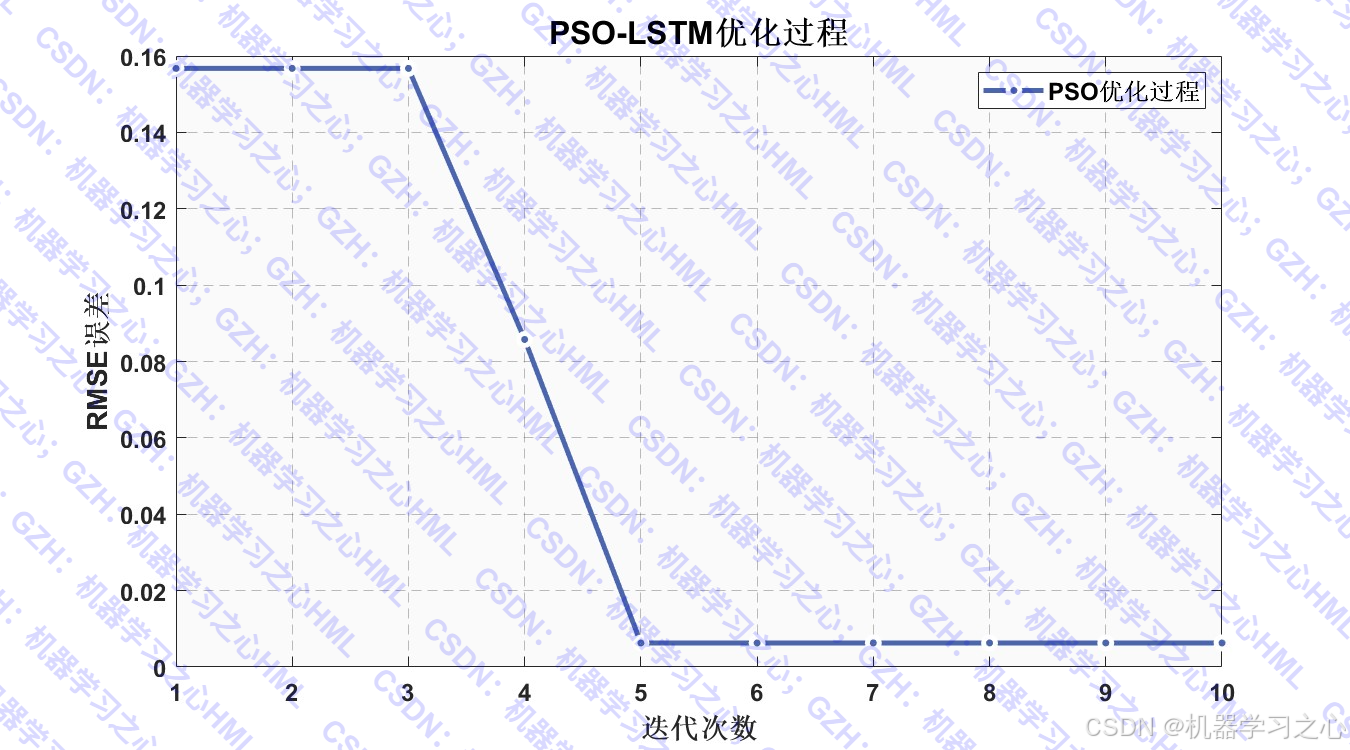
- 智能优化LSTM超参数:使用PSO算法优化LSTM的隐藏层神经元数和初始学习率
- 多输出回归预测:支持多个输出变量的同时预测
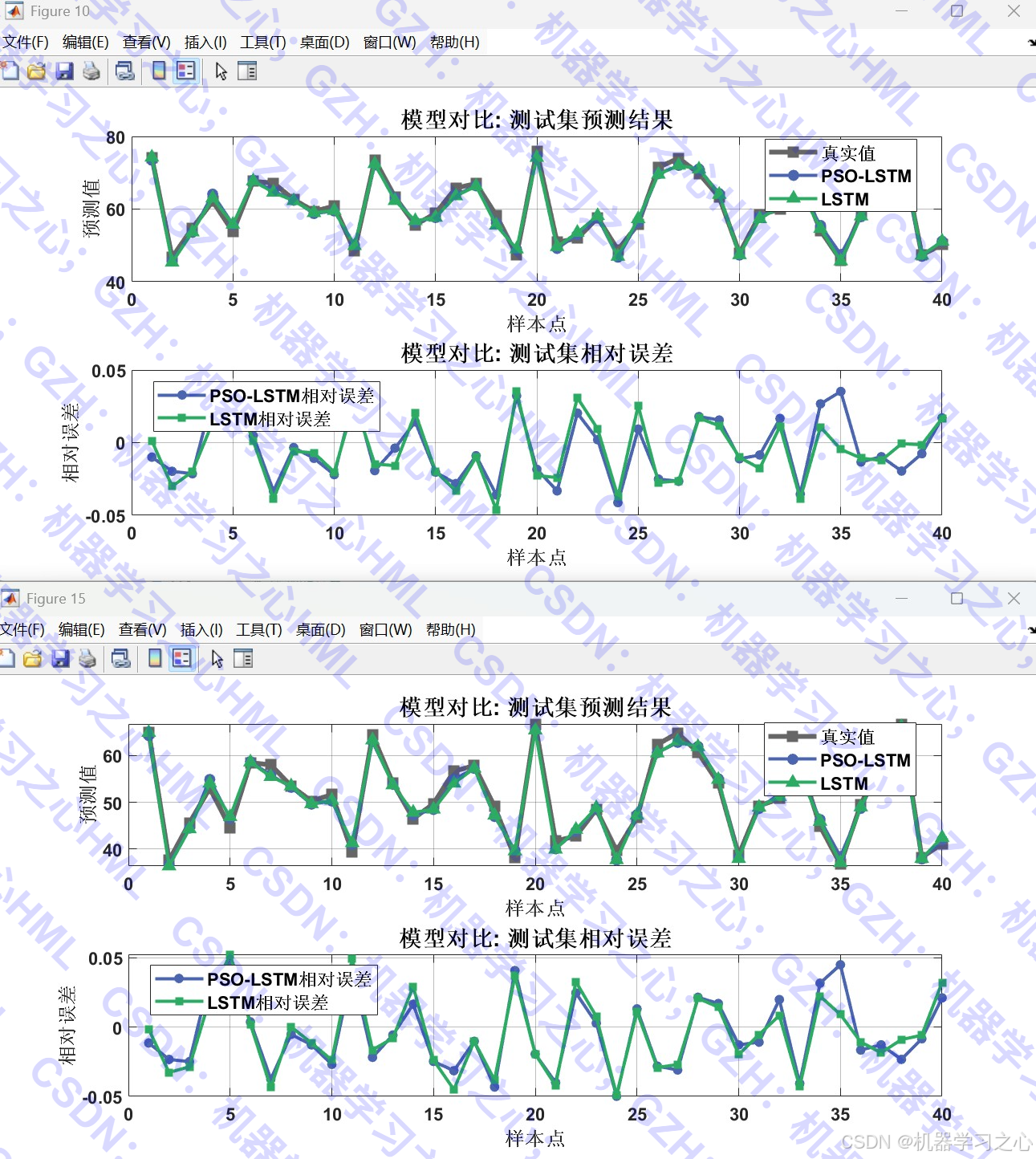
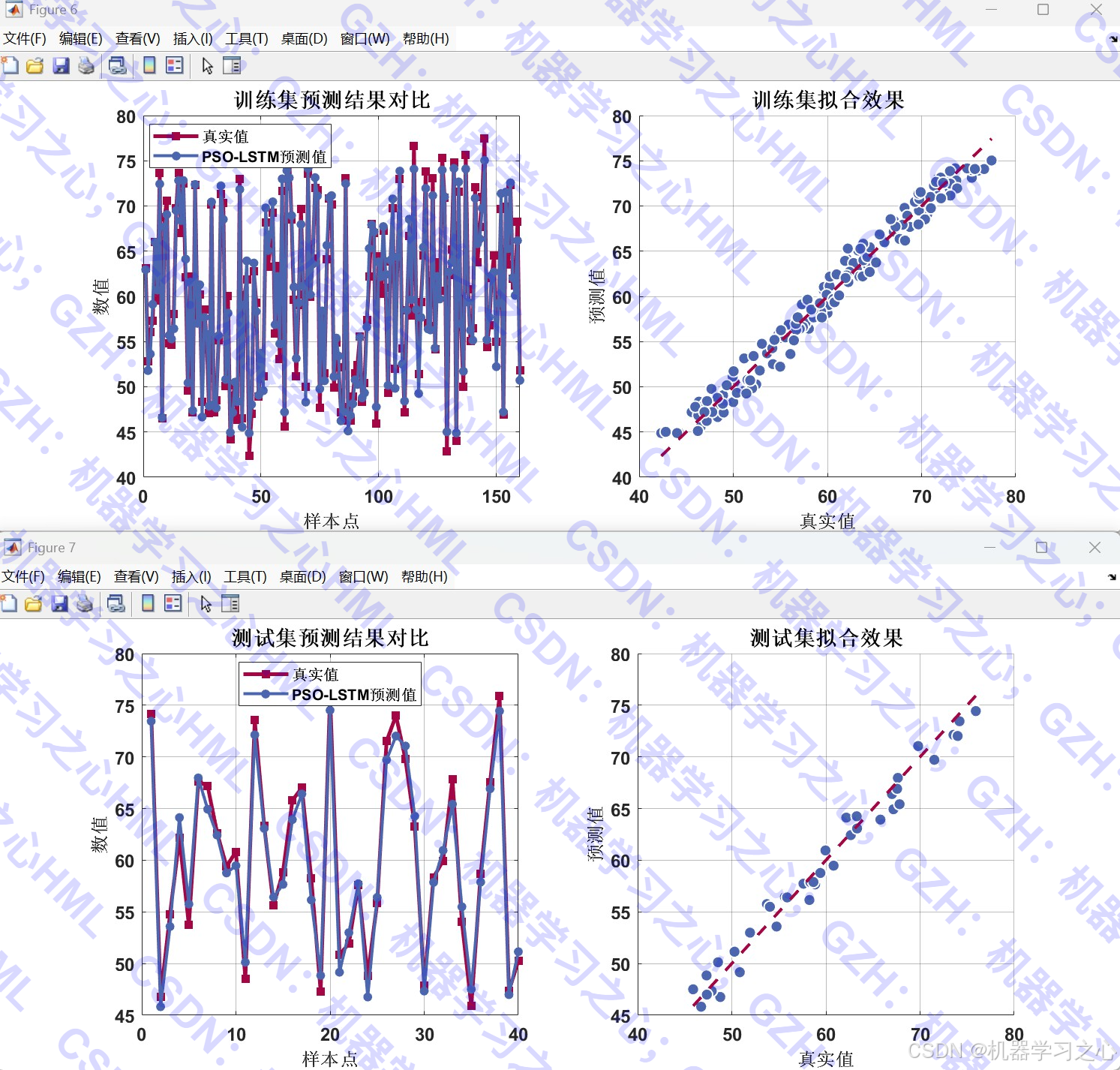
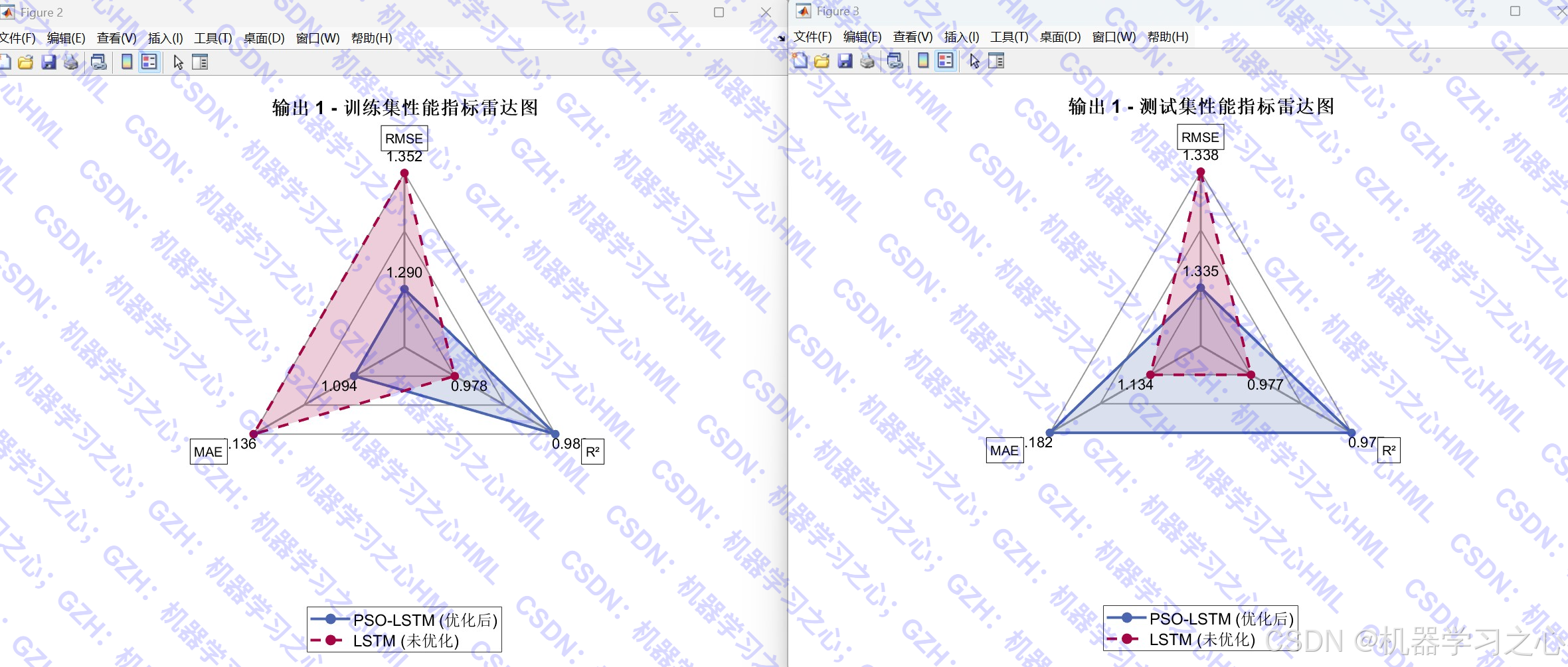
- 模型性能对比:比较优化前后LSTM模型的预测精度
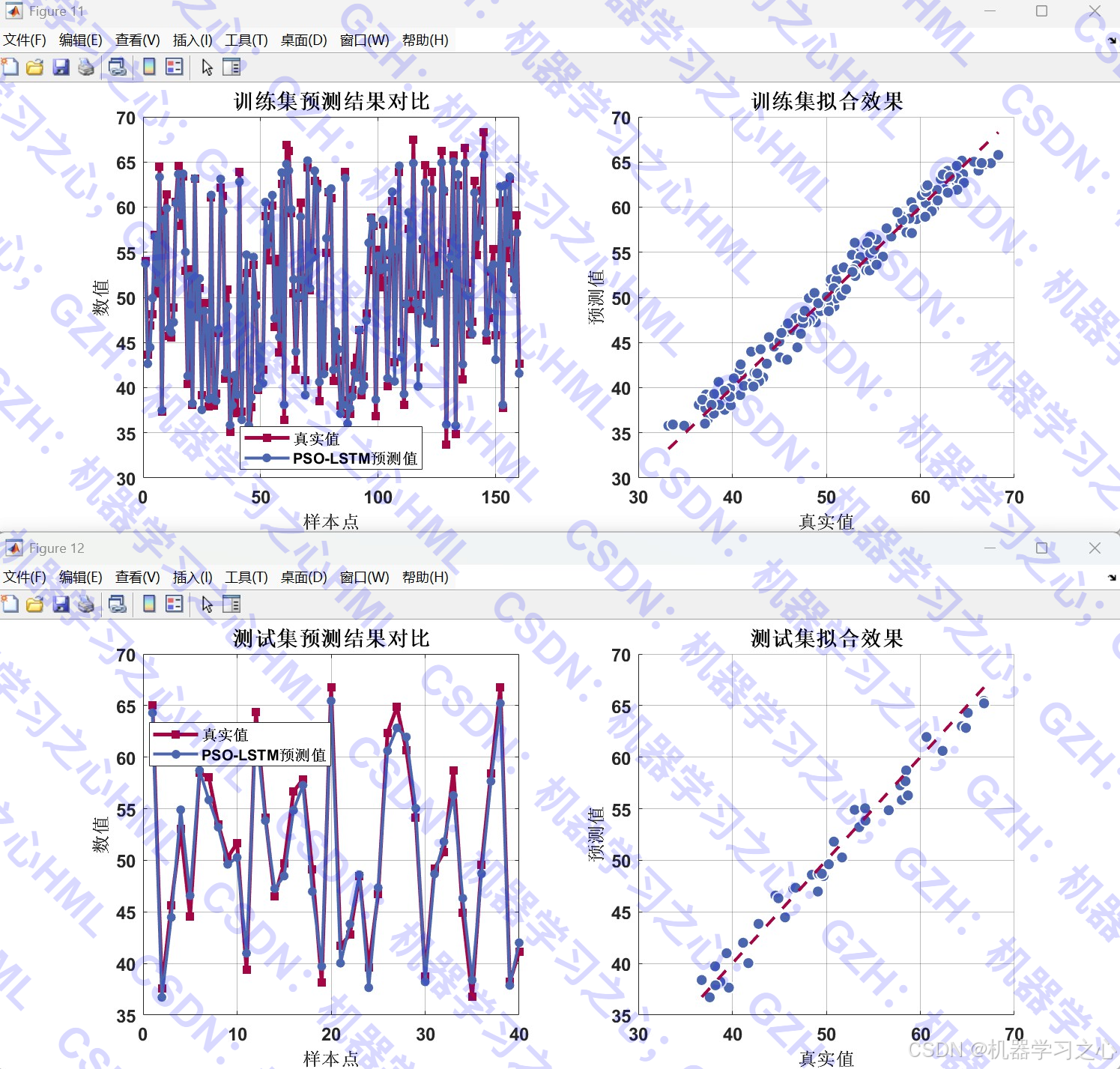
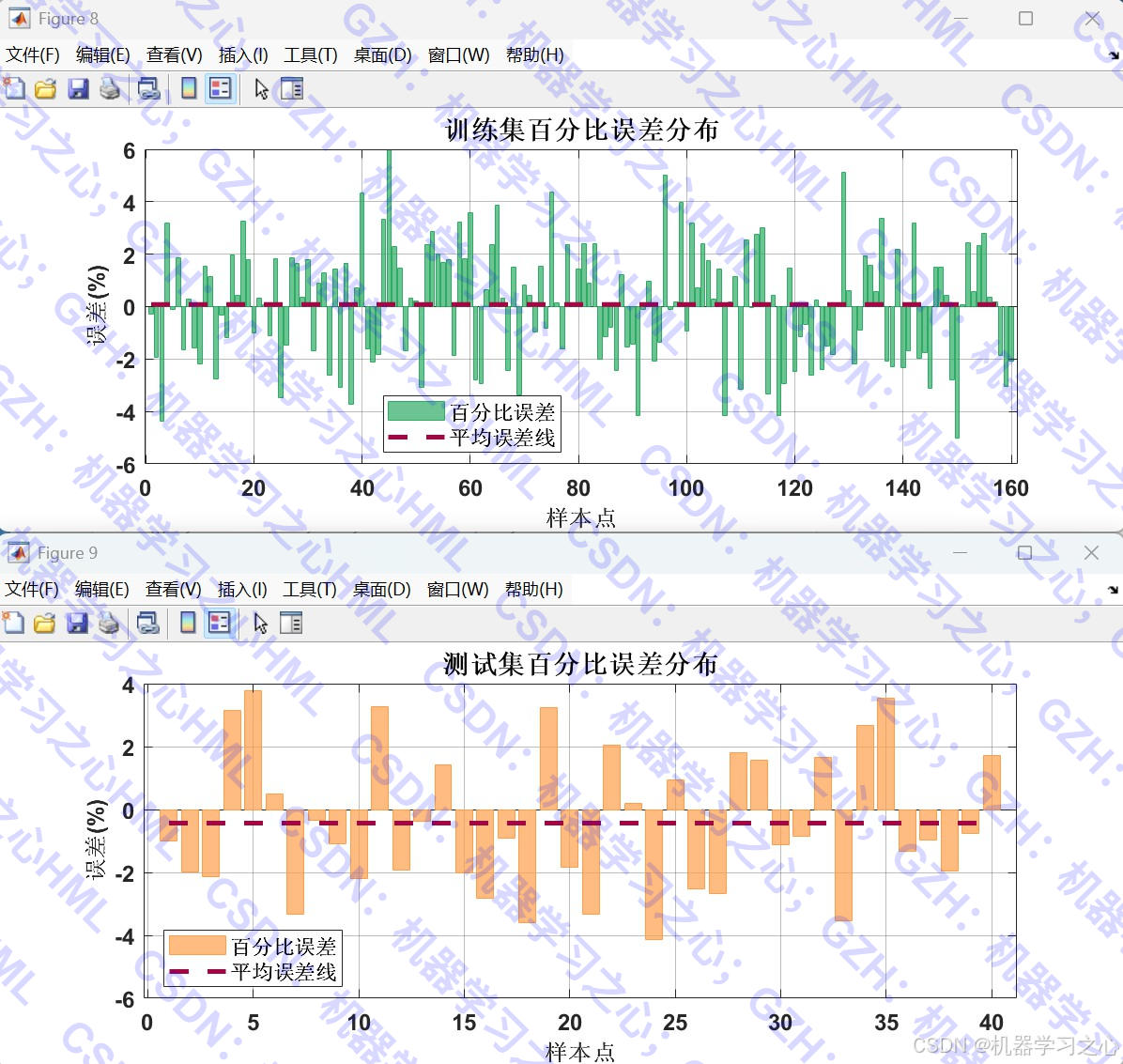
- 可视化分析:提供丰富的图表展示预测结果和性能指标
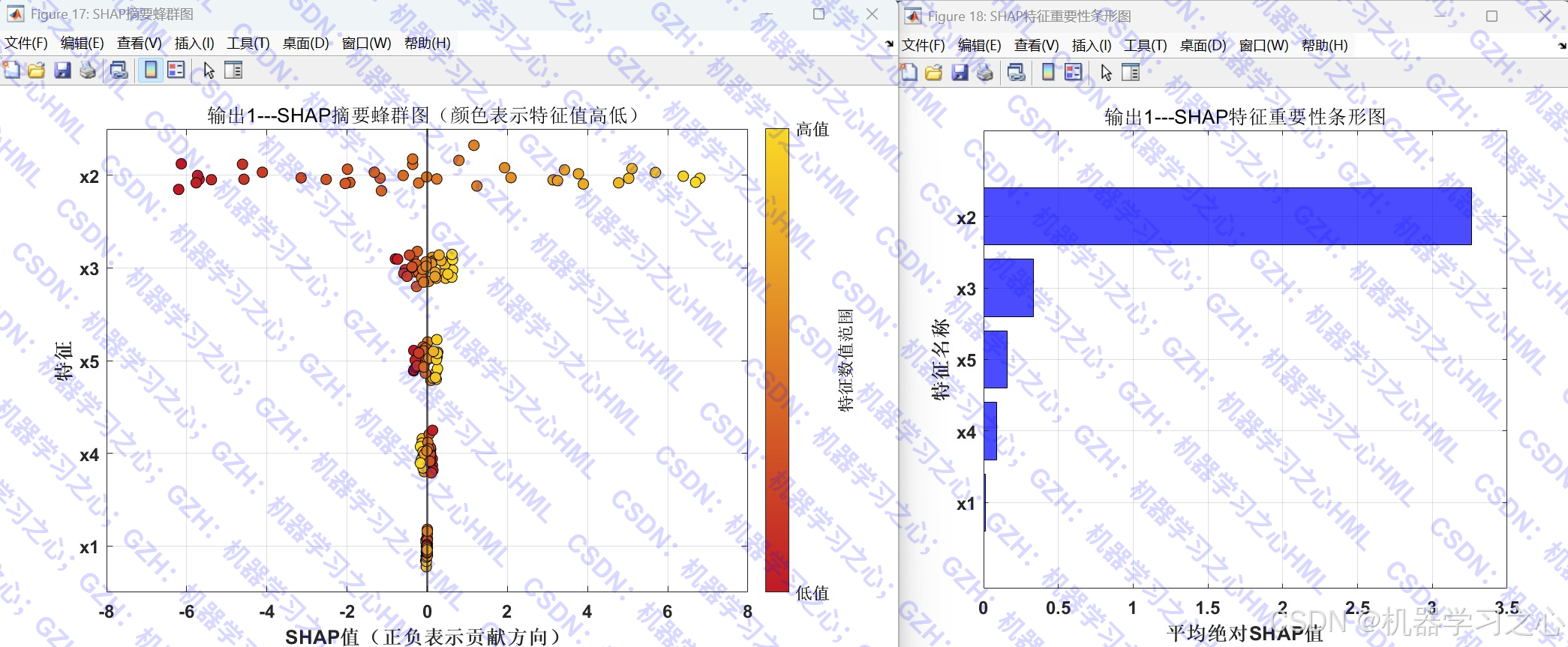
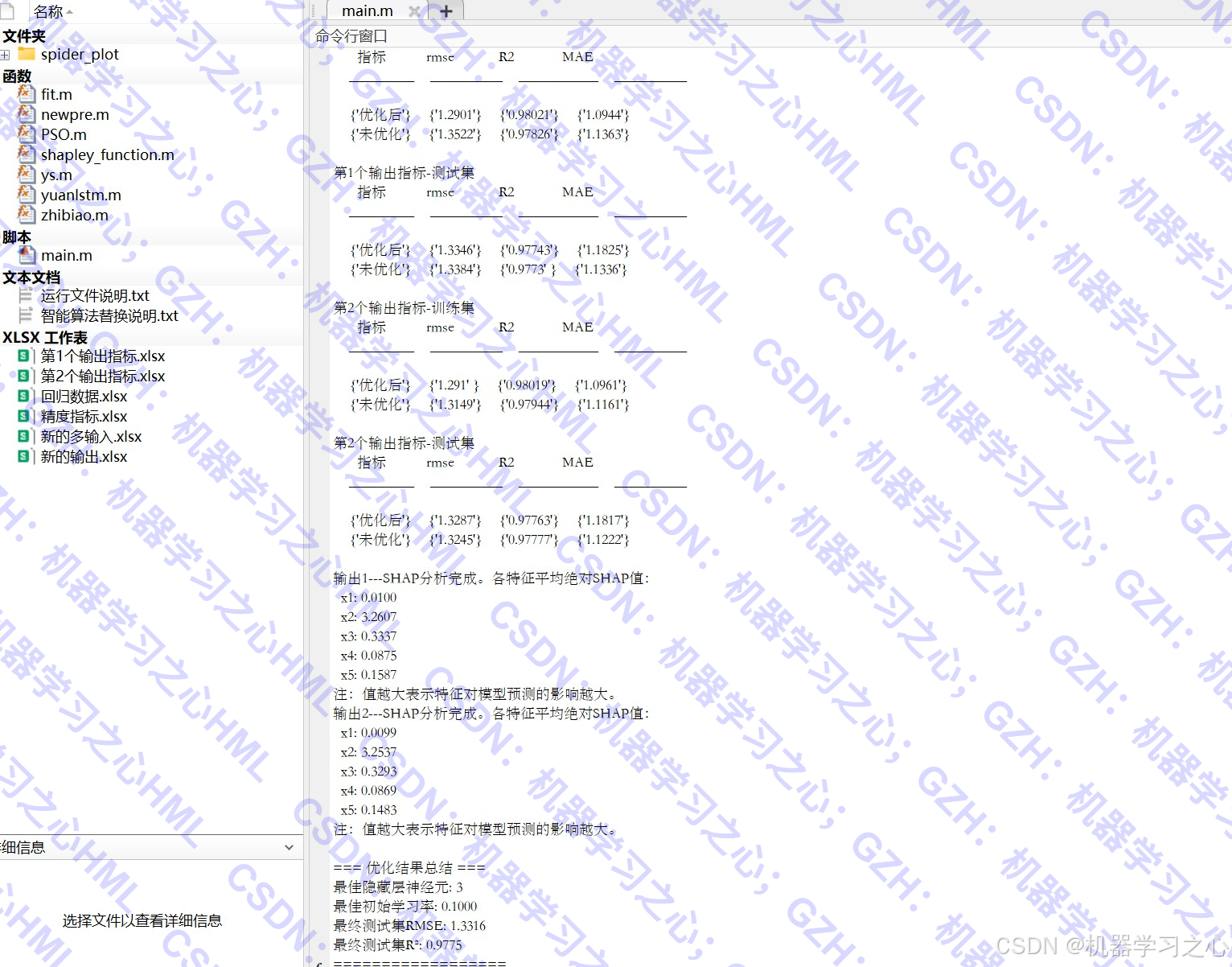
- 特征重要性分析:计算SHAP值分析特征贡献度
2. 算法步骤
1. 数据预处理 → 2. PSO超参数优化 → 3. LSTM模型训练 →
4. 预测与反归一化 → 5. 性能评估 → 6. 可视化展示3. 技术路线
核心算法组合:
- PSO(粒子群优化):超参数寻优
- LSTM(长短期记忆网络):序列数据建模
- 混沌映射:PSO初始化增强(Tent、Chebyshev等9种映射)
数据处理:
- Min-Max归一化(0-1范围)
- 训练集/测试集划分(80%/20%)
- 数据打乱选项
4. 公式原理
PSO更新公式:
vi(t+1)=w⋅vi(t)+c1⋅r1⋅(pbesti−xi(t))+c2⋅r2⋅(gbest−xi(t)) v_i(t+1) = w·v_i(t) + c1·r1·(pbest_i - x_i(t)) + c2·r2·(gbest - x_i(t)) vi(t+1)=w⋅vi(t)+c1⋅r1⋅(pbesti−xi(t))+c2⋅r2⋅(gbest−xi(t))
xi(t+1)=xi(t)+vi(t+1) x_i(t+1) = x_i(t) + v_i(t+1) xi(t+1)=xi(t)+vi(t+1)
LSTM核心公式:
遗忘门:ft=σ(Wf⋅[ht−1,xt]+bf) 遗忘门:f_t = σ(W_f·[h_{t-1}, x_t] + b_f) 遗忘门:ft=σ(Wf⋅[ht−1,xt]+bf)
输入门:it=σ(Wi⋅[ht−1,xt]+bi) 输入门:i_t = σ(W_i·[h_{t-1}, x_t] + b_i) 输入门:it=σ(Wi⋅[ht−1,xt]+bi)
输出门:ot=σ(Wo⋅[ht−1,xt]+bo) 输出门:o_t = σ(W_o·[h_{t-1}, x_t] + b_o) 输出门:ot=σ(Wo⋅[ht−1,xt]+bo)
细胞状态:Ct=ft⋅Ct−1+it⋅tanh(Wc⋅[ht−1,xt]+bc) 细胞状态:C_t = f_t·C_{t-1} + i_t·tanh(W_c·[h_{t-1}, x_t] + b_c) 细胞状态:Ct=ft⋅Ct−1+it⋅tanh(Wc⋅[ht−1,xt]+bc)
隐藏状态:ht=ot⋅tanh(Ct) 隐藏状态:h_t = o_t·tanh(C_t) 隐藏状态:ht=ot⋅tanh(Ct)
5. 参数设定
PSO参数:
- 种群大小:N=10
- 最大迭代次数:Max_iteration=10
- 搜索范围:
- 隐藏层神经元:[2, 20]
- 初始学习率:[0.001, 0.1]
LSTM参数:
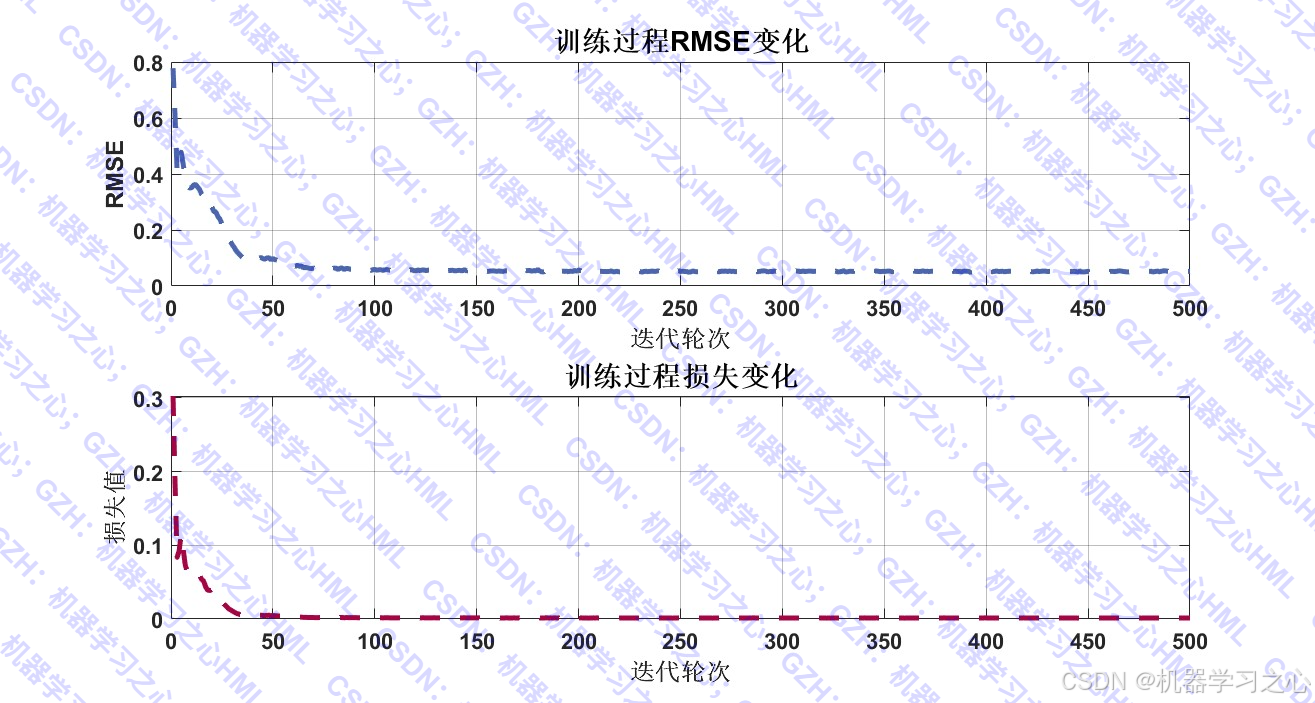
- 最大训练轮数:500
- 优化器:Adam
- 学习率下降:每200轮下降10倍
- 激活函数:ReLU
6. 运行环境
- 平台:MATLAB2020b及以上
- 必需工具箱 :
- Deep Learning Toolbox(LSTM)
- Optimization Toolbox(PSO)
- 自定义spider_plot工具箱(雷达图)
7. 应用场景
适用领域:
- 多变量回归:产品质量预测、设备故障诊断
- 工程优化:参数优化、性能预测
典型应用:
- 金融市场的多指标预测
- 工业生产过程的质量控制
- 能源系统的负荷预测
- 环境监测的多参数预测