c++之AVL树

(一) 前言

在 C 语言和 C++ 的学习过程中，我们接触了多种数据查找方法。这些方法在发展过程中呈现出逐步优化的特点，各自适用于不同场景，也存在一定局限：

1. **暴力搜索：**需要对数据进行全面遍历，时间效率极低，在数据量较大时几乎不具备实用价值；
2. **二分搜索：**虽能依托有序数据实现高效查找，但前提是数据必须始终保持有序状态。当面对插入、删除操作（尤其是中间位置的操作）时，需频繁调整数据位置以维持有序性，导致维护成本过高；
3. **二叉搜索树：**理想状态下可实现高效查找，但在极端场景（如数据持续单向插入）中，树结构会退化为链表，此时查找效率大幅下降至 O (n)，稳定性较差；
4. **二叉平衡搜索树（如 AVL 树、红黑树）：**通过特定机制维持树的平衡性，解决了二叉搜索树的退化问题；
5. **多叉平衡搜索树（如 B 树、B + 树等系列结构）：**进一步优化了平衡机制，更适用于磁盘等外部存储场景；
6. **哈希表：**通过哈希函数直接映射数据位置，可实现近似 O (1) 的查找效率，但存在哈希冲突等问题需特殊处理。

目前我们已学习了前三种方法。为了在实际应用中实现更快速、更稳定的查找操作，接下来我们将从二叉平衡搜索树开始逐步深入，首先学习 AVL 树的相关知识。

---

(二) 正文

(1) AVL树的概念

由来：

二叉搜索树虽能提升查找效率，但当插入的数据集为有序或接近有序时，树结构会退化为单支树（类似链表）。此时，查找元素的操作效率会降至与顺序表相同的 O (n)，性能大幅下降。为解决这一问题，1962 年俄罗斯数学家 G.M.Adelson-Velskii 和 E.M.Landis 提出了一种改进方案 ：在向二叉搜索树插入新结点后，通过特定调整机制，确保树中每个结点的左右子树高度之差的绝对值不超过 1。这一机制能有效控制树的整体高度，从而减少平均搜索长度，基于此思想的树结构被命名为 AVL 树（以两位发明者的名字命名）。

具体来说，一棵 AVL 树要么是空树，要么是满足以下性质的二叉搜索树：

• 其左、右子树均为 AVL 树；
• 左、右子树的高度之差（简称平衡因子，平衡因子 = 右子树高度 - 左子树高度）的绝对值不超过 1（即平衡因子（balance factor ）的可能取值为 - 1、0 或 1）

小思考：
为什么 AVL 树的 "平衡" 定义为 "平衡因子的绝对值不超过 1"，而非要求左右子树高度完全相等？

其实，若能让所有结点的左右子树高度完全相等（即满二叉树状态），理论上查找效率会更高。但在实际插入、删除操作中，要始终维持这种绝对平衡的状态难度极大 ------ 任何微小的结构变动都可能打破平衡，需要进行大量调整，反而会降低整体效率。因此，AVL 树采用 "平衡因子绝对值≤1" 的标准，是在理想平衡与实际可操作性之间做出的折中方案：既保证了树的高度被有效控制（近似平衡），又使调整成本维持在合理范围内。

(2) AVL树的模拟

依旧得先定义树和树的节点

要实现 AVL 树，首先需要定义其节点结构及树的基本框架。AVL 树的节点除了存储数据、左 / 右孩子指针外，还需额外保存一个 "平衡因子"（Balance Factor），用于衡量节点左右子树的高度差（平衡因子 = 右子树高度 - 左子树高度）。

代码如下：

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V> *_right;
	AVLTreeNode<K, V>* _parent;
	int _bf;

	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		,_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
    //内容
private:
	Node* _root = nullptr;
};

我的内容主要介绍插入和插入中的旋转，因为大家在准备 AVL 树的知识的面试时不用太焦虑于 "完整手撕整个 AVL 树"------ 因为完整实现要处理太多细节，比如父指针维护、平衡因子的连锁调整、删除后的复杂逻辑等，代码量大还容易出错，面试时间有限，既难完成也容易让面试官和自己都陷入混乱，所以实际面试里很少要求这么做 。反**而更要聚焦 "插入操作和插入中的旋转"：插入是旋转的 "触发场景"，旋转是 AVL 树维护平衡的核心手段，尤其是 LL 右旋、RR 左旋、LR 先左后右、RL 先右后左这四种基础旋转，**它们作为最小考察单元，代码量少、逻辑聚焦，面试官常通过 "让你手撕某一种旋转" 或 "讲解插入 + 旋转的配合逻辑"，来判断你是否真的懂 AVL 树的平衡本质，所以重点关注这两部分，对应对 AVL 树的面试考察会更高效、更有针对性。

2.1 插入操作

AVL 树本质上是一种自平衡的二叉搜索树，其插入过程可分为两个核心步骤：

1. 按二叉搜索树规则插入新节点： 遵循二叉搜索树的插入逻辑（即比当前节点小的元素插入左子树，比当前节点大的元素插入右子树），确定新节点的最终位置。
2. **调整平衡因子并维护平衡性：**新节点插入后，可能会破坏 AVL 树的平衡性（即存在节点的平衡因子绝对值大于 1）。因此需要从新节点开始向上回溯，更新各祖先节点的平衡因子，并检测是否需要通过旋转恢复平衡。

平衡因子的更新规则

设新插入的节点为cur，其直接父节点为parent。cur插入后，parent的平衡因子必然需要调整，具体规则如下：

• 若cur插入到parent的左子树中，则parent的平衡因子需减 1（左子树高度增加，平衡因子左减）；
• 若cur插入到parent的右子树中，则parent的平衡因子需加 1（右子树高度增加，平衡因子右加）。

平衡因子的三种可能结果及处理方式

更新后，parent的平衡因子可能出现以下三种情况，需分别处理：

• 平衡因子为 0： 说明插入前parent的平衡因子为 ±1（左 / 右子树高度差为 1），插入后因另一侧子树高度增加，平衡因子被调整为 0（左右子树高度相等）。此时以parent为根的子树高度未发生变化，且满足 AVL 树的平衡条件（平衡因子绝对值≤1），插入操作在此分支可终止，无需继续向上更新。
• 平衡因子为 ±1： 说明插入前parent的平衡因子为 0（左右子树高度相等），插入后因某一侧子树高度增加，平衡因子变为 ±1（高度差为 1）。此时以parent为根的子树高度增加了 1，可能会影响其祖先节点的平衡因子，因此需要继续向上回溯，更新更上层祖先节点的平衡因子。
• 平衡因子为 ±2： 此时pParent的平衡因子绝对值超过 1，违反了 AVL 树的平衡条件，导致子树失衡。这种情况下必须通过旋转操作（包括左旋、右旋、左右双旋、右左双旋）调整子树结构，使平衡因子恢复至合法范围（绝对值≤1），旋转后子树高度与插入前一致，无需继续向上更新（旋转后面在介绍）

通过以上步骤，AVL 树可在插入新节点后始终维持平衡性，保证后续的查找、删除等操作仍能保持 O (log n) 的时间复杂度。

代码如下：

     //在AVL树中插入值为kv的节点
	bool Insert(const pair<K, V>& kv)
	{
		//按照二叉搜索树的方式插入新节点
		if (_root == nullptr)
		{
			Node* newNode = new Node(kv);
			_root = newNode;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > kv)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		Node* newNode = new Node(kv);
		if (cur->_kv.first > kv)
		{
			cur->_left = newNode;
		}
		else
		{
			cur->_right = newNode;
		}
		 
		//调整节点的平衡因子
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_bf--;
			}
			else
			{
				parent->_bf++;
			}

			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//旋转

			}
			else
			{
				assert(false);
			}
		}
	}

旋转为AVL树的重点和难点和难点有应为后面学习的红黑树也会用到，所有我们需要认真学习并掌握。

2.2 旋转操作

旋转时需要注意的问题：

1. 保持他是搜索树
2. 变成平衡树且降低这个子树的高度

1. 新节点插入较高右子树的右侧---右右：左单旋

其中核心操作为：

parent->_right =cur->_left;

cur->_left = parent;

我们先来看看图解，抽象的图片：

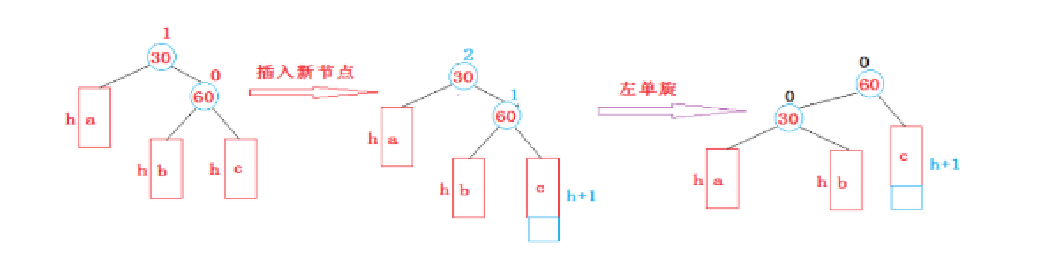
我带大家来具体分析一下吧：

需要注意的是：a/b/c是符合AVL规则的子树

当 h == 0 时：

当 h == 1 时：

当 h == 3 时：

由于情况较为多样，我们可以通过分析子树的可能形态来统计总情况数：

先知道abc分别可以去什么先，对后面分析也会有帮助

总结：

子树a、b可分别取x、y、z中的任意一种 （x、y、z为三种不同的子树结构，可结合原图中的示意图理解），子树c固定为z （因为x或y会使平衡因子为1，不符合右右情况的前提）。
故可以知道：

插入之前的情况为 3*3*1 种

插入的位置情况有 4 种

故总情况为： 3*3*4 =36 种

当然后面的可以自己分析一下（后面几个旋转因为会粗略解释）

代码如下：

void RotateL(Node* parent)
{
	Node* cur = parent->_right;
	Node* curleft = cur->_left;

	parent->_right = curleft;
	if (curleft != nullptr)
	{
		curleft->_parent = parent;
	}

	cur->_left = parent;
	Node* ppnode = parent->_parent;
	parent->_parent = cur;

	if (parent == _root)
	{
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = cur;
		}
		else
		{
			ppnode->_right = cur;
		}

		cur->_parent = ppnode;
	}

	cur->_bf = parent->_bf = 0;
}

2. 新节点插入较高左子树的左侧---左左：右单旋

其中核心操作为：

parent->_left =cur->_right;

cur->_right = parent;

我们先来看看图解，抽象的图片：

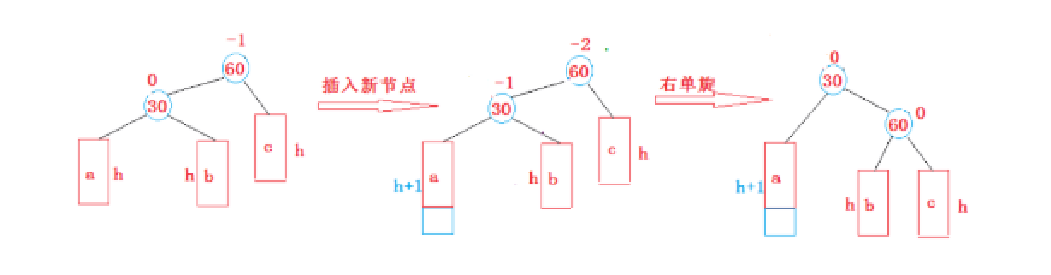
具体图：

代码如下：

void RotateR(Node* parent)
{
	Node* cur = parent->_left;
	Node* curright = cur->_right;

	parent->_left = curright;
	if (curright != nullptr)
	{
		curright->_parent = parent;
	}

	cur->_right = parent;
	Node* ppnode = parent->_parent;
	parent->_parent = cur;

	if (parent == _root)
	{
		_root = cur;
		cur->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = cur;
		}
		else
		{
			ppnode->_right = cur;
		}
		cur->_parent = ppnode;
	}

	cur->_bf = parent->_bf = 0;
}

3.新节点插入较高左子树的右侧---左右：先左单旋再右单旋

他主要是复用了左单旋，右单旋，复杂的部分为各个位置的bf值，图片就会很好解释

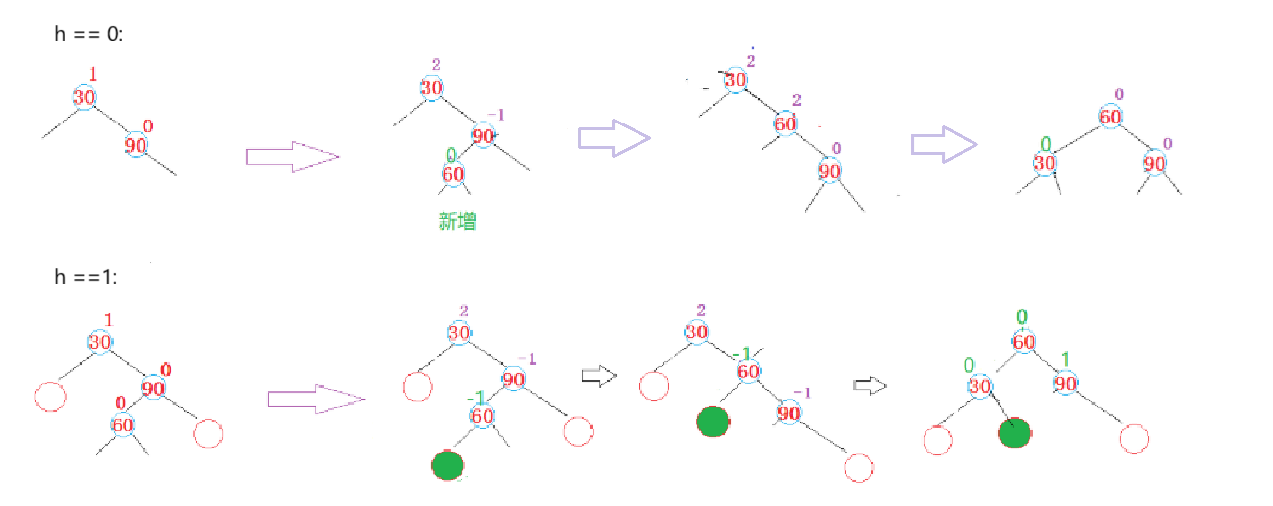
我们先来看看图解，抽象的图片：令 bf = curright->_bf

当 bf == 0 时：

当30为parent时，90为cur，此时60为新增时，看最后一个图可以知道

cur->_bf = 0; curright->_bf = 0; parent->_bf = 0;

当 bf == -1 时：

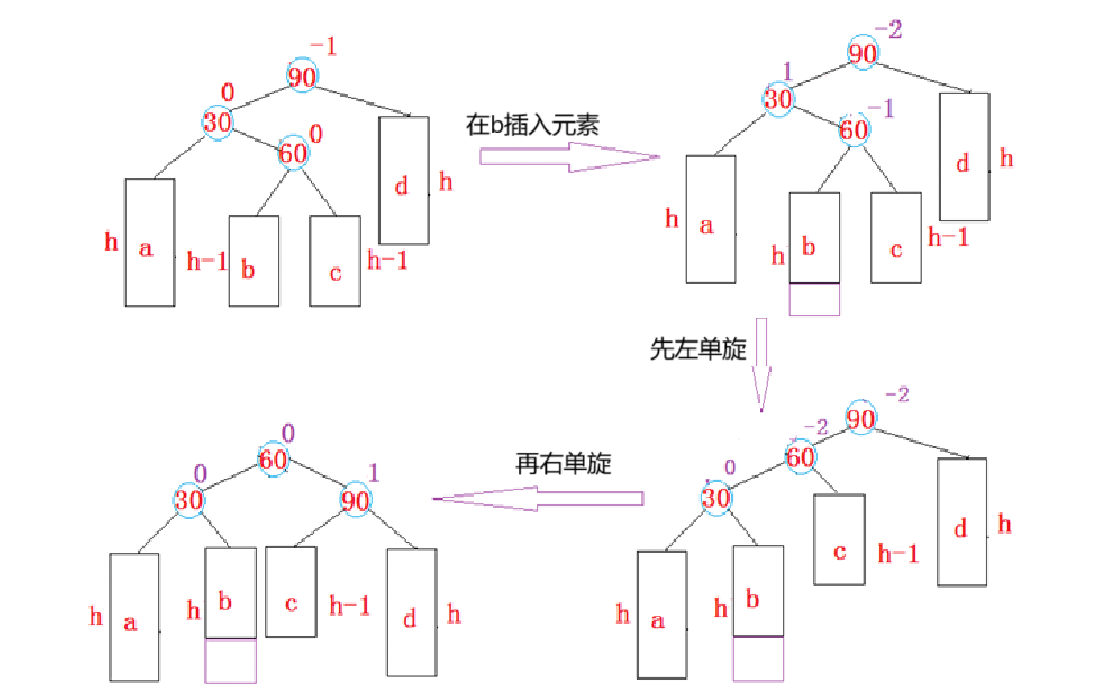
当90为parent时，30为cur，60为curright，此时在b位置新增时，看最后一个图可以知道

cur->_bf = 0; curright->_bf = 0; parent->_bf = 1;

当 bf == 1 时：

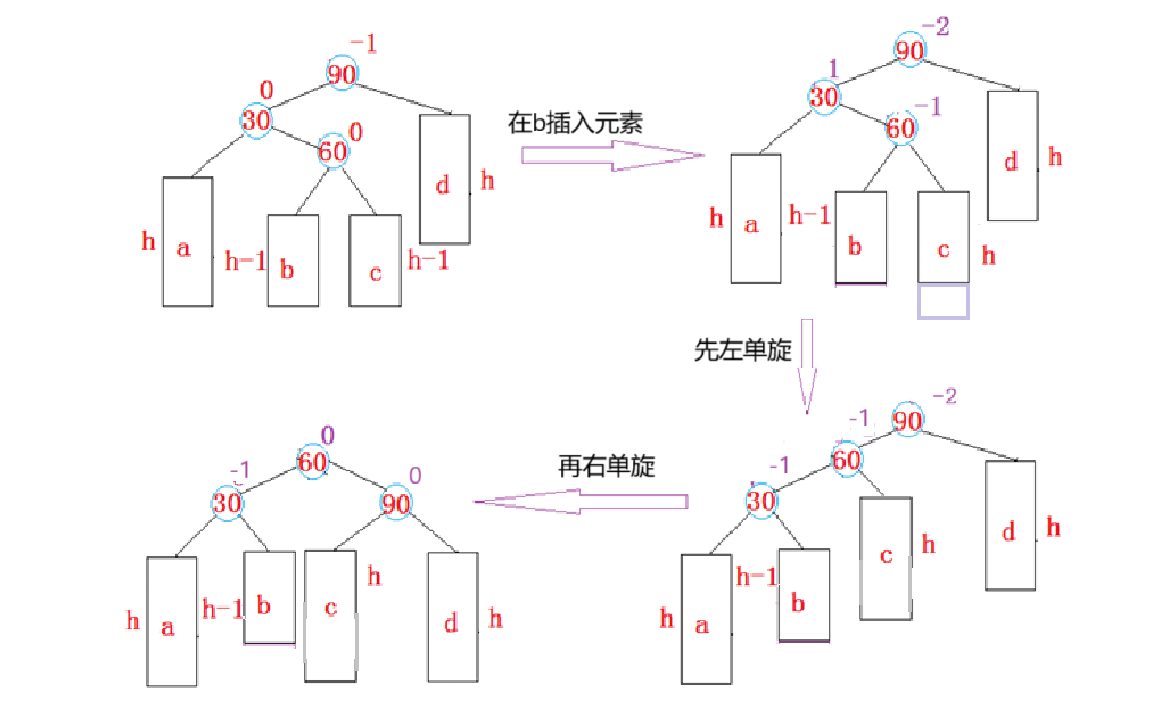
当90为parent时，30为cur，60为curright，此时在c位置新增时，看最后一个图可以知道

cur->_bf = -1; curright->_bf = 0; parent->_bf = 0;

具体图：

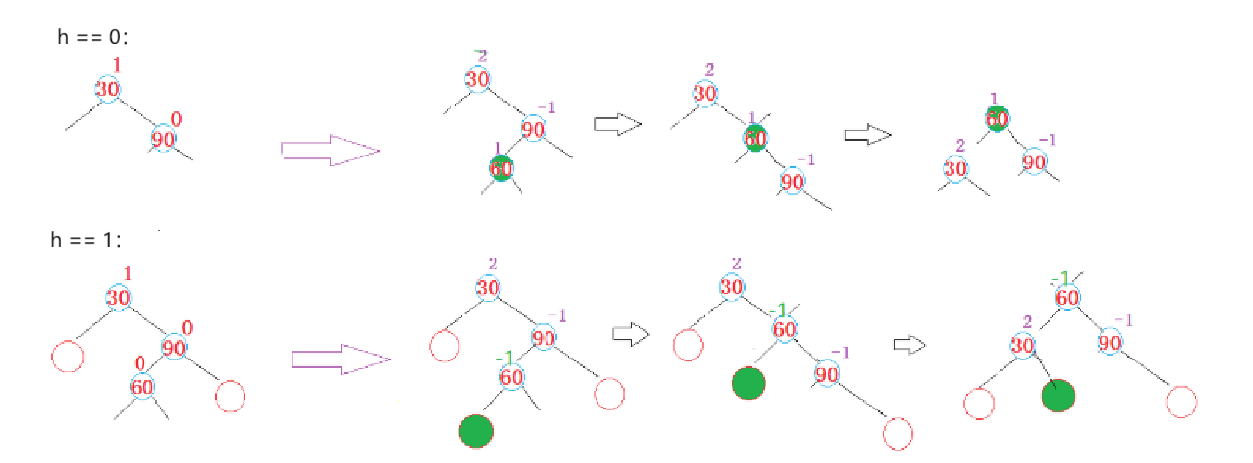
代码如下：

void RotateLR(Node* parent)
{
	Node* cur = parent->_left;
	Node* curright = cur->_right;
	int bf = curright->_bf;

	RotateL(parent->_left);
	RotateR(parent);

	if (bf == 0)
	{
		cur->_bf = 0;
		curright->_bf = 0;
		parent->_bf = 0;
	}
	else if (bf == 1)
	{
		cur->_bf = -1;
		curright->_bf = 0;
		parent->_bf = 0;
	}
	else if (bf == -1)
	{
		cur->_bf = 0;
		curright->_bf = 0;
		parent->_bf = 1;
	}
	else
	{
		assert(false);
	}
}

4. 新节点插入较高右子树的左侧---右左：先右单旋再左单旋

他也主要是复用了左单旋，右单旋，复杂的部分为各个位置的bf值，图片就会很好解释

我们先来看看图解，抽象的图片：令 bf = curleft->_bf

当 bf == 0 时：

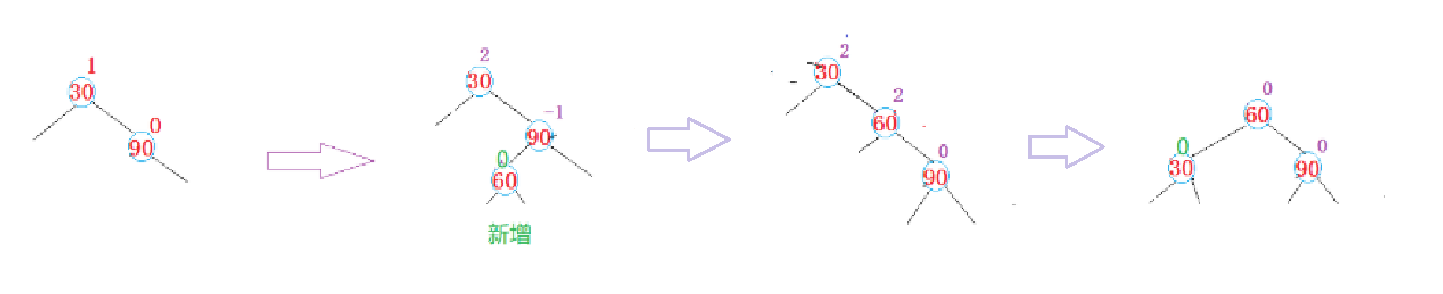
当30为parent时，90为cur，此时60为新增时，看最后一个图可以知道

cur->_bf = 0; curright->_bf = 0; parent->_bf = 0;

当 bf == 1 时：

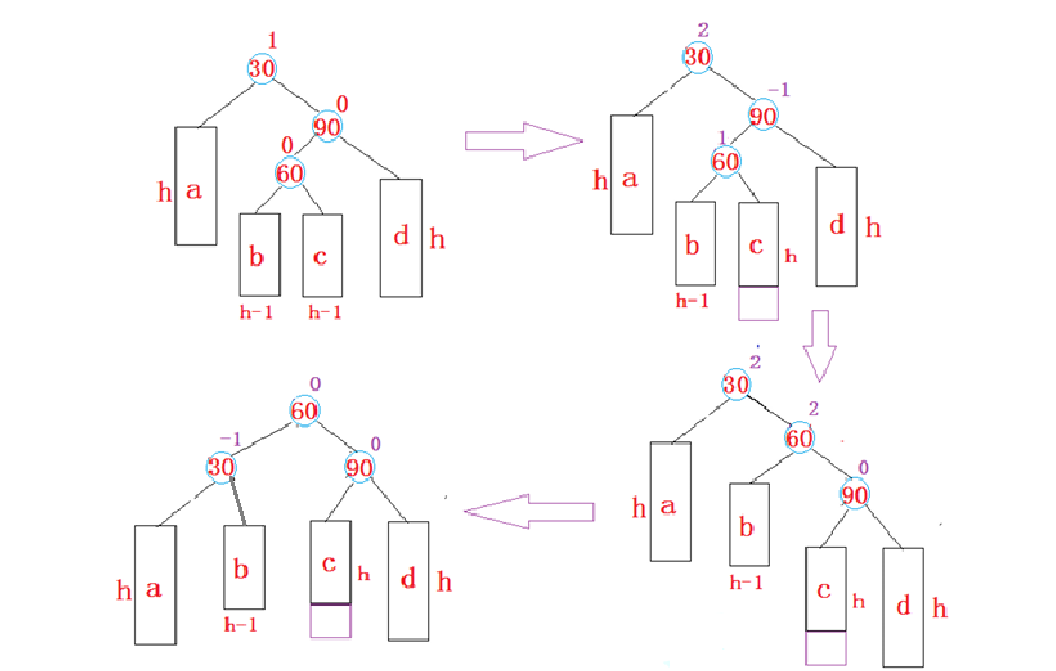
当90为parent时，30为cur，60为curright，此时在c位置新增时，看最后一个图可以知道

cur->_bf = 0; curright->_bf = 0; parent->_bf = -1;

当 bf == -1 时：

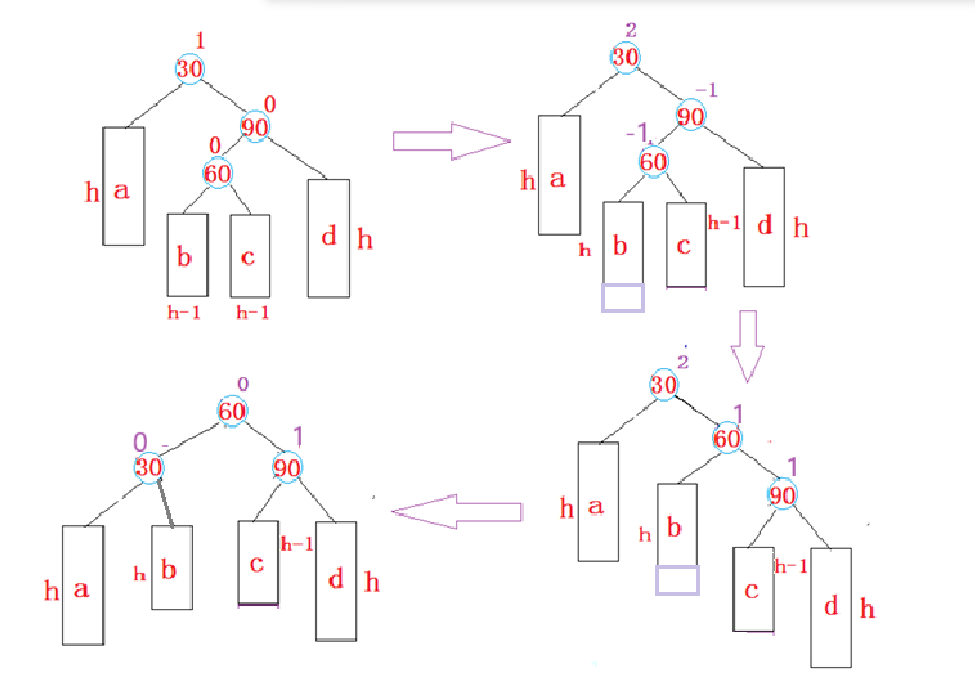
当90为parent时，30为cur，60为curright，此时在c位置新增时，看最后一个图可以知道

cur->_bf = 1; curright->_bf = 0; parent->_bf = 0;

具体图像：

代码如下：

void RotateRL(Node* parent)
{
	Node* cur = parent->_right;
	Node* curleft = cur->_left;
	int bf = curleft->_bf;

	RotateR(parent->_right);
	RotateL(parent);

	if (bf == 0)
	{
		cur->_bf = 0;
		curleft->_bf = 0;
		parent->_bf = 0;
	}
	else if (bf == 1)
	{
		cur->_bf = 0;
		curleft->_bf = 0;
		parent->_bf = -1;
	}
	else if (bf == -1)
	{
		cur->_bf = 1;
		curleft->_bf = 0;
		parent->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

总结------AVL树的旋转直线单旋，折现双旋，左边高向右边旋转，右边高向左边旋转。

---

(3) AVL树的验证

在 AVL 树的实现中，代码逻辑涉及节点插入、平衡因子调整和四种旋转操作，细节繁多且极易出错 ------ 比如之前遇到的指针方向写反、变量名拼写错误、旋转后平衡因子未重置等问题。面对这类复杂代码，我们不能只依赖逐行检查，更需要通过「验证函数」提前排查整体问题，再配合高效的调试技巧精准定位错误，大幅提升排错效率。

验证函数
手写的IsAVLTree()函数是 AVL 树的 "纠错第一道防线"，它的核心作用是通过递归从两个维度验证树的合法性，避免错误隐藏在复杂逻辑中，也可以让我们快速发现是哪里不对：

代码如下：

bool IsAVLTree()
{
	return _IsAVLTree(_root);
}

private:
	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);

		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	bool _IsAVLTree(Node* root)
	{
		if (root == nullptr)
			return true;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);

		if (rightHeight - leftHeight != root->_bf)
		{
			cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;
			return false;
		}

		return abs(rightHeight - leftHeight) < 2
			&& _IsAVLTree(root->_left)
			&& _IsAVLTree(root->_right);
	}

简单来说，IsAVLTree()能帮我们先判断 "树是否真的平衡"，再决定是否深入调试细节 ------ 如果它返回 true，说明整体逻辑无大错；若返回 false，再针对性找问题，避免做无用功。

精准定位细节错误：

当IsAVLTree()提示异常，或插入特定数据时程序崩溃（比如插入 15 时树结构断裂），普通断点会因循环次数多（如插入上万条数据）而频繁触发，效率极低。这时候两种断点技巧能帮我们 "精准狙击" 错误：
技巧 1：条件断点 ------ 循环中只停在 "出问题的那次执行"
操作方式：

1. 在循环内部（比如插入逻辑的for (auto e : v)循环内）打一个普通断点；
2. 右键点击断点，选择「条件」（不同调试器 wording 可能不同，如 VS 中是 "Condition"）；
3. 输入触发条件，比如「e == 15」（表示 "只有当插入的键值是 15 时，才暂停程序"）。

但是他还不是特别灵活，技巧二更为灵活好用。

技巧 2：手动代码断点 ------ 灵活定位 "特定逻辑节点"

操作方式：

在需要定位的逻辑附近，手动写一段 "触发代码"，本质是通过 "无关变量赋值" 强制创造一个可断点的位置。比如插入序列中，我们怀疑插入 e=15 时平衡因子调整错误，就可以这样写：

for (auto e : v)
{
    avlt.Insert(make_pair(e, e));
    // 手动断点：当e=11时，暂停并检查状态
    if (e == 15)
    {
        int x = 0;  // 在这行打普通断点
    }
}

为什么中间要写一个int x = 0;

• 因为不写的话面对空白是停不下来的，不方便我们进行更细节的调查。

这种方式的优势是灵活可控，哪怕调试环境不支持复杂条件断点，也能精准定位到我们关心的逻辑节点。

测试用例：

void test1()
{
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVLTree<int, int> t;
	for (auto e : a)
	{
		t.Insert(make_pair(e, e));
		cout << "Insert:" << e << "->" << t.IsAVLTree() << endl;
	}

}


void test2()
{
	const int N = 10000000;
	vector<int> v;
	v.reserve(N);
	srand(time(0));

	for (size_t i = 0; i < N; i++)
	{
		v.push_back(i);
	}

	AVLTree<int, int> avlt;
	for (auto e : v)
	{
		avlt.Insert(make_pair(e, e));
		//cout << "Insert:" << e << "->" << t.IsAVLTree() << endl;
	}

	cout << avlt.IsAVLTree() << endl;

}

完整代码------博主的gitee

---

(4) AVL树的删除（简易版）

在 AVL 树的学习和面试场景中，删除操作的优先级远低于插入

1. 实际业务中 AVL 树的删除需求较少，更多是 "插入 + 查询" 的场景；
2. 删除的逻辑复杂度远高于插入，细节繁琐且面试极少要求完整实现；

因此这里仅做简易梳理，帮助大家建立 "删除逻辑的整体认知" 即可。

4.1 删除的核心步骤（基于二叉搜索树 + 平衡维护）
AVL 树的删除本质是 "先按二叉搜索树（BST）规则删节点，再向上追溯维护平衡"，整体可拆为三步：
第一步：按 BST 规则查找并删除目标节点
第二步：向上追溯更新平衡因子

从删除节点的父节点（记为parent）开始，逐层向上更新平衡因子，更新规则与插入相反，但判断逻辑更复杂：

• **若删除的是parent的左子树节点：**左子树高度减少 1，parent的平衡因子需+1（平衡因子 = 右子树高度 - 左子树高度，左减则整体加）；
• **若删除的是parent的右子树节点：**右子树高度减少 1，parent的平衡因子需-1。

更新后需根据parent的平衡因子判断是否继续向上：

• **若parent的平衡因子变为±1：**说明删除前parent的平衡因子是0（原来左右平衡，现在一边减 1，高度差 1），子树整体高度未变（因为原来高度由高的一侧决定，现在高的一侧没变），无需继续向上更新；
• **若parent的平衡因子变为0：**说明删除前parent的平衡因子是±1（原来高度差 1，现在平衡），子树整体高度减少 1（原来高度由高的一侧决定，现在高的一侧减 1，整体高度降 1），需要继续向上更新父节点的平衡因子；
• **若parent的平衡因子变为±2：**子树失衡，需要进入第三步 ------ 旋转调整。

第三步：失衡时的旋转调整

删除的旋转判断更复杂：删除时，失衡节点的平衡因子变化可能来自 "另一侧子树的高度减少"，需要结合 "哪一侧子树高度更低" 来判断旋转类型，且旋转后可能仍需继续向上检查（插入时旋转后通常无需继续，删除可能触发连锁失衡）。

4.2 删除的核心难点

很多人看完步骤会觉得 "好像也不难"，但实际动手实现时会发现处处是坑，核心难点在于两点：

1. 平衡因子的 "追溯逻辑" 难把控
2. 旋转的 "触发条件" 更难判断

总之------如果你对删除逻辑好奇，建议先彻底掌握 "插入 + 四种旋转" 的完整逻辑（能独立写出无 bug 的插入和验证代码），再去深入研究删除------ 可以在网上搜索一下或者看看书了解。

但是可以不必强求自己手写完整的删除代码（面试几乎不考），能讲清 "删除的三步核心逻辑" 和 "为什么比插入复杂"，就已经达到学习目标了。

---

以上就是C++之AVL树的学习一点点，后续的会继续更新这个算法的题目，我们将留待日后进行。希望这些知识能为你带来帮助！如果觉得内容实用，欢迎点赞支持~ 若发现任何问题或有改进建议，也请随时与我交流。感谢你的阅读！