TensorFlow（1）

一、TensorFlow 简介

TensorFlow 简介 | 菜鸟教程

二、环境搭建

TensorFlow 环境搭建 | 菜鸟教程

三、TensorFlow 核心概念

TensorFlow 核心概念 | 菜鸟教程

在 TensorFlow 中，张量（Tensor） 是最核心的数据结构，可以简单理解为 "多维数组"，但比普通数组多了一些特殊属性，是 TensorFlow 中数据传递和计算的基本单位。

1. 张量的本质：多维数组的 "升级版"

张量可以看作是对 "标量、向量、矩阵" 的泛化：

• 0 维张量 ：就是标量（单个数值），比如 3、42（对应之前代码中 f 的结果）。
• 1 维张量 ：就是向量（一串数值），比如 [1, 2, 3]。
• 2 维张量 ：就是矩阵（行列组成的表格），比如 [[1,2], [3,4]]。
• 3 维及以上张量 ：更高维度的数组，比如 "批量图片数据" 可能是 (10, 28, 28)（10 张 28×28 的灰度图），"视频数据" 可能是 (5, 10, 28, 28)（5 段视频，每段 10 帧，每帧 28×28 像素）。

2. 张量的关键属性

每个张量都有两个核心属性，这也是你在输出中经常看到的：

• 形状（shape） ：描述张量的维度和每个维度的长度。比如 shape=() 是 0 维（标量），shape=(3,) 是 1 维（3 个元素），shape=(2,3) 是 2 维（2 行 3 列）。
• 数据类型（dtype） ：描述张量中数值的类型，比如 int32（32 位整数）、float32（32 位浮点数，深度学习中最常用）、string（字符串）等。

3. 张量和普通数组的区别：为什么叫 "升级版"？

张量虽然长得像 NumPy 数组，但有两个关键特性让它更适合深度学习：

• 支持 GPU 加速：张量可以被自动放到 GPU 上计算（NumPy 数组只能在 CPU 上运行），大幅提升大规模计算的速度。
• 与计算图绑定：张量在计算图中流动（"Flow"），TensorFlow 会记录张量的运算路径，从而实现自动求导（反向传播的核心），这对训练神经网络至关重要。
• 不可变性 ：普通张量（tf.Tensor）一旦创建，其值不能直接修改（类似 Python 中的元组），只能通过运算生成新的张量。如果需要可修改的变量（比如神经网络的权重），则需要用 tf.Variable（它本质是 "可训练的张量"）。

# 导入TensorFlow库，简写为tf
import tensorflow as tf

# 创建一个二维常量张量（不可修改的张量）
# 数据为2行3列的矩阵：[[1,2,3], [4,5,6]]
# tf.constant用于定义值不可变的张量，常用于存储输入数据或常量参数
tensor = tf.constant([[1,2,3],[4,5,6]])

# 打印张量的形状（shape）
# shape表示张量的维度信息，格式为(维度1长度, 维度2长度, ...)
# 此处输出为(2, 3)，表示这是一个2行3列的二维张量
print(tensor.shape)

# 打印张量的数据类型（dtype）
# 默认为int32（32位整数），也可通过dtype参数指定（如tf.float32）
print(tensor.dtype)

# 打印张量的秩（rank）
# 秩即张量的维度数量，二维张量的秩为2，可理解为"阶数"
# tf.rank()返回的是一个标量张量，此处输出tf.Tensor(2, shape=(), dtype=int32)
print(tf.rank(tensor))

# 打印张量所在的计算设备（device）
# 表示该张量在哪个设备上存储和计算（如CPU:0、GPU:0）
# 默认为CPU，若有可用GPU且配置正确，可能显示GPU设备
print(tensor.device)

4、变量（Variable）

# 导入TensorFlow库，简写为tf以便后续调用
import tensorflow as tf

# 创建一个名为weight的可训练变量（常用于神经网络权重参数）
# 初始值通过tf.random.normal([2, 3])生成：
# - 形状为2行3列的二维张量
# - 元素值服从标准正态分布（均值0，标准差1的随机数）
weight = tf.Variable(tf.random.normal([2, 3]))

# 创建一个名为bias的可训练变量（常用于神经网络偏置参数）
# 初始值通过tf.zeros([3])生成：
# - 形状为1维、包含3个元素的张量
# - 所有元素值均为0.0
bias = tf.Variable(tf.zeros([3]))

# 打印weight的初始状态
# 输出包含变量类型、形状、数据类型及随机生成的初始值（每次运行结果不同）
print(weight)

# 打印提示信息，标识即将展示修改后的weight
print("修改后")

# 使用assign()方法整体更新weight的值
# tf.ones([2, 3])生成2行3列的全1矩阵，替换weight的原有值
# 注意：tf.Variable必须通过assign()方法修改值，不能直接用=赋值（确保梯度追踪正常）
weight.assign(tf.ones([2, 3]))

# 打印整体更新后的weight
# 此时所有元素值均变为1.0
print(weight)

# 打印提示信息，标识即将展示部分更新后的weight
print("部分更新")

# 通过索引定位并更新weight的特定元素
# weight[0, 0]表示第1行第1列的元素，将其值修改为5.0
weight[0, 0].assign(5.0)

# 打印部分更新后的weight
# 仅第1行第1列的元素变为5.0，其他元素保持1.0
print(weight)

5、数据流动和自动微分

前向传播

可以把神经网络想象成一条 "数据流水线"：输入数据从 "起点"（输入层）流入，经过若干个 "加工站"（隐藏层），每个加工站对数据进行特定处理，最终从 "终点"（输出层）产出结果。整个过程中，数据始终沿着 "输入层→隐藏层→输出层" 的单向路径流动，没有反向反馈，因此称为 "前向"。

反向传播

反向传播是神经网络训练的核心算法，用于根据模型预测误差调整网络参数（权重和偏置），最终让模型的预测结果更接近真实值。它与前向传播配合，构成了神经网络 "学习" 的过程。

可以把反向传播理解为 "从结果追溯原因" 的过程：

• 首先计算输出层的误差（预测值与真实值的差距）；
• 然后将误差 "反向传递" 到上一层（隐藏层），计算隐藏层参数对误差的贡献；
• 重复这个过程，直到传递到输入层，最终得到所有参数（权重、偏置）的梯度；
• 最后用优化器（如 SGD、Adam）根据梯度更新参数（例如：权重 = 权重 - 学习率 × 梯度）。

这个过程的数学基础是链式法则（复合函数求导），通过逐层拆解误差的来源，高效计算每个参数的梯度（避免了暴力求解的高复杂度）。

隐藏层（Hidden Layer）

隐藏层是神经网络中介于输入层和输出层之间的所有层，因其 "不直接接触原始输入和最终输出" 而得名。它是神经网络 "提取特征、学习规律" 的核心。

• 输入层：直接接收原始数据（如图片的像素、文本的特征），仅负责传递数据，不做处理；
• 输出层：输出最终结果（如分类标签、预测值）；
• 隐藏层：对输入数据进行 "逐层加工"，从简单特征中提取复杂特征。例如：
  • 识别图片时，第一层隐藏层可能学习 "边缘" 特征，第二层学习 "纹理" 特征，第三层学习 "部件"（如眼睛、鼻子）特征，最终输出层整合这些特征判断 "是否为人脸"。

没有隐藏层的网络（如感知机）只能学习线性关系，而加入隐藏层后，神经网络可以通过 "线性变换 + 非线性激活" 的堆叠，学习复杂的非线性关系（如图像、语言、声音等）。

# 导入TensorFlow库，用于构建和运行神经网络
import tensorflow as tf

# 1. 定义输入数据
# 输入特征x：形状为[1, 2]的二维张量（1个样本，每个样本有2个特征）
# 这里的输入是[[1.0, 2.0]]，表示一个样本的两个特征值分别为1.0和2.0
x = tf.constant([[1.0, 2.0]])
print(tf.shape(x))  # tf.Tensor([1 2], shape=(2,), dtype=int32)

# 2. 定义模型参数（权重和偏置）

# w1：输入层到隐藏层的权重矩阵
# 形状为[2, 3]：2对应输入层神经元数量（特征数），3对应隐藏层神经元数量
# 用tf.random.normal初始化：随机生成符合正态分布的初始值
w1 = tf.Variable(tf.random.normal([2, 3]))

# b1：隐藏层的偏置项
# 形状为[3]：与隐藏层神经元数量一致（每个神经元对应一个偏置）
# 用tf.zeros初始化：初始值为0
b1 = tf.Variable(tf.zeros([3]))

# w2：隐藏层到输出层的权重矩阵
# 形状为[3, 1]：3对应隐藏层神经元数量，1对应输出层神经元数量
w2 = tf.Variable(tf.random.normal([3, 1]))

# b2：输出层的偏置项
# 形状为[1]：与输出层神经元数量一致
b2 = tf.Variable(tf.zeros([1]))

# 3. 执行前向传播（核心过程）
# 3.1 计算隐藏层输出
# 步骤1：输入x与权重w1矩阵相乘（tf.matmul实现矩阵乘法），再加上偏置b1
# 得到隐藏层的净输入（线性变换结果）：shape为[1, 3]（1个样本，3个隐藏神经元）
# 步骤2：通过ReLU激活函数（tf.nn.relu）将线性输出转换为非线性输出
hidden = tf.nn.relu(tf.matmul(x, w1) + b1)  # 隐藏层最终输出，shape为[1, 3]

# 3.2 计算输出层结果
# 隐藏层输出hidden与权重w2矩阵相乘，再加上偏置b2
# 这里没有用激活函数（适合回归任务），输出为最终预测结果
output = tf.matmul(hidden, w2) + b2  # 输出层结果，shape为[1, 1]（1个样本的预测值）

# 打印输出层的预测结果
print(output)  #tf.Tensor([[0.]], shape=(1, 1), dtype=float32)

自动微分（Automatic Differentiation）

# 导入TensorFlow库，用于数值计算和自动求导
import tensorflow as tf

# 定义一个可训练变量x，初始值为3.0
# tf.Variable表示这是一个"可被跟踪"的变量，后续计算梯度时会被GradientTape记录
x = tf.Variable(3.0)

# 使用tf.GradientTape()创建一个"梯度磁带"上下文环境
# 作用：在这个环境中执行的所有张量运算都会被自动记录下来，用于后续求导
with tf.GradientTape() as tape:
    # 定义函数y = x² + 2x + 1，这是我们要求导的目标函数
    # 由于x是tf.Variable，且运算在tape的上下文内，所以计算过程会被完整记录
    y = x**2 + 2*x + 1  # 等价于 y = (x+1)²

# 调用tape的gradient方法计算梯度：求y对x的导数dy/dx
# 参数说明：
#   第一个参数y：被求导的函数结果（因变量）
#   第二个参数x：求导的变量（自变量）
# 返回值是一个张量，表示在x=3.0处的导数值
gradient = tape.gradient(y, x)

# 打印结果：根据求导公式，y = x²+2x+1的导数是dy/dx = 2x + 2
# 当x=3时，2*3 + 2 = 8，因此输出为8.0
print(f"当 x=3 时，dy/dx = {gradient}")  # 输出：当 x=3 时，dy/dx = 8.0

1. with tf.GradientTape() as tape:

   • 这行代码创建了一个 GradientTape 对象（相当于打开录像机），并通过 as tape 给它起了个名字 tape。
   • with 语句的作用是 "划定录像范围"：只有在这个缩进块里的运算才会被记录，出了这个块，"录像机" 就自动关闭了。

2. 缩进块内的运算 y = x**2 + 2*x + 1

   • 因为 x 是 tf.Variable（可训练变量，相当于需要求导的 "未知数"），GradientTape 会重点跟踪它的变化。
   • 它会记录：x 先被平方得到 ，然后 x 乘以 2 得到 2x，最后两者加 1 得到 y。这些步骤都是后续求导的依据。

3. tape.gradient(y, x)

   • 当你调用这个方法时，tape 会根据刚才记录的步骤，反向计算 y 对 x 的导数。
   • 例如，根据记录的 "x 平方" 步骤，它知道这一步的导数是 2x；"x 乘以 2" 的导数是 2；最后相加的导数就是各部分导数相加（2x+2）。

with tf.GradientTape() as tape: 的作用是划定一个 "需要被记录的计算范围"，让 TensorFlow 自动跟踪这个范围内的运算步骤，以便后续高效地计算梯度（导数）。这是实现反向传播的底层技术支撑。

四、TensorFlow 张量操作

TensorFlow 张量操作 | 菜鸟教程

张量的聚合操作

tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
sum_axis0 = tf.reduce_sum(tensor, 0)  # 沿第0维(行)求和 → [5,7,9]

• TensorFlow 中，维度（axis）的编号从 0 开始：
  • 对于 2 维张量（矩阵），第 0 维（axis=0）表示 "行方向"（纵向）。
• 沿第 0 维求和的含义是：将不同行中同一列的元素相加。
• 计算过程：
  • 第 0 列：第一行的 1 + 第二行的 4 = 5
  • 第 1 列：第一行的 2 + 第二行的 5 = 7
  • 第 2 列：第一行的 3 + 第二行的 6 = 9
• 结果是一个 1 维张量[5,7,9]（原张量的行维度被缩减，保留列维度）。

sum_axis1 = tf.reduce_sum(tensor, 1)  # 沿第1维(列)求和 → [6,15]

沿第 1 维（列）求和，意思是对每一行内部的所有列元素分别求和：

• 第 0 行的元素是 [1, 2, 3]，求和结果为：1 + 2 + 3 = 6；
• 第 1 行的元素是 [4, 5, 6]，求和结果为：4 + 5 + 6 = 15。

五、TensorFlow 高级 API - Keras

TensorFlow 高级 API -- Keras | 菜鸟教程

Keras 和 TensorFlow 都是深度学习领域的重要工具，但两者定位和功能有明显区别，核心关系可以概括为：Keras 是高层深度学习 API，而 TensorFlow 是底层深度学习框架；Keras 可以运行在 TensorFlow 等底层框架之上。具体区别如下：

1. 定位与层级不同

• TensorFlow ：是一个底层深度学习框架，提供了完整的数值计算、自动微分、分布式训练等底层功能，支持从基础算子（如矩阵乘法、卷积运算）到复杂模型的搭建。它更接近 "工具库"，灵活性极高，但使用时需要编写较多底层代码（例如手动定义计算图、参数更新逻辑等）。

• Keras ：是一个高层深度学习 API，设计理念是 "用户友好、模块化、可扩展"，封装了大量常用的模型组件（如层、优化器、损失函数），允许用户用极简的代码快速搭建和训练模型。它更像 "模型搭建工具"，隐藏了底层实现细节，专注于模型的逻辑结构（如 "添加一个卷积层""编译模型""训练模型"）。

2. 依赖关系

• 早期 Keras 是独立的 API，可以兼容多个底层框架（如 TensorFlow、Theano、CNTK）。
• 2017 年 TensorFlow 官方将 Keras 整合为其官方高层 API（即 tf.keras），现在大多数情况下提到的 Keras 其实是 tf.keras，与 TensorFlow 深度绑定，成为 TensorFlow 的一部分。
• 简单说：Keras 是 TensorFlow 的 "前端"（用户接口），TensorFlow 是 Keras 的 "后端"（计算引擎）。

3. 使用场景

• 用 Keras（tf.keras）：适合快速原型开发、初学者入门、实现标准化模型（如简单的 CNN、RNN）。例：用几行代码搭建一个神经网络：

from tensorflow import keras
model = keras.Sequential([
    keras.layers.Dense(64, activation='relu'),
    keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='categorical_crossentropy')
model.fit(x_train, y_train, epochs=10)

• 用原生 TensorFlow：适合需要深度定制底层逻辑的场景，例如设计自定义算子、优化分布式训练策略、实现复杂的模型结构（如自定义反向传播）。例：用原生 TensorFlow 定义简单计算（需手动处理会话 / 计算图）：

import tensorflow as tf
x = tf.constant([1, 2, 3])
y = tf.square(x)
with tf.Session() as sess:
    print(sess.run(y))  # 输出 [1, 4, 9]

4. 灵活性与简洁性权衡

• Keras 以 "简洁" 为核心，牺牲了部分灵活性：用 Keras 能快速实现模型，但对底层计算的控制能力较弱。
• TensorFlow 以 "灵活" 为核心，牺牲了部分简洁性：可以精确控制模型的每一步计算，但代码量更大，学习曲线更陡。

总结

• 关系 ：Keras 是高层 API，TensorFlow 是底层框架；tf.keras 是 TensorFlow 官方推荐的高层接口。
• 选择 ：快速开发用 Keras（tf.keras），深度定制用原生 TensorFlow。实际应用中，两者常结合使用（例如用 Keras 搭模型，用 TensorFlow 优化底层细节）。

六、Keras 第一个神经网络

Keras 第一个神经网络 | 菜鸟教程

6.1 必须了解

神经网络中，"神经元"（Neuron）是模拟生物神经元（大脑中的神经细胞）结构和功能的基本计算单元，是构建神经网络的核心组件。理解神经元的工作原理，是理解整个神经网络的基础。

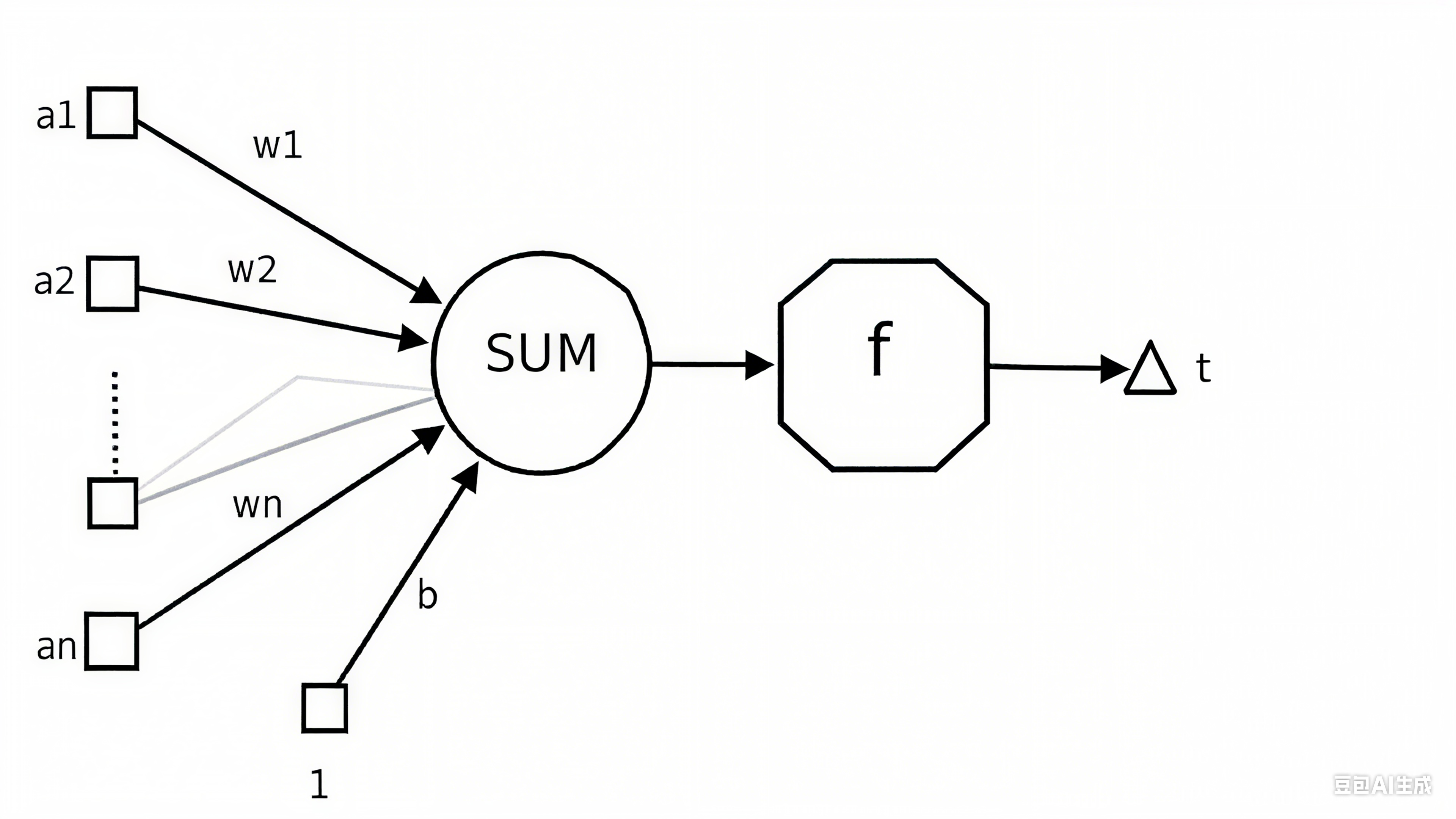
6.1.1 人工神经元的结构与工作原理

一个人工神经元的核心功能是：接收输入信号 → 计算加权和 → 应用激活函数 → 输出结果。具体步骤如下：

1. 接收输入

神经元会接收来自上一层（或外部数据）的多个输入信号，记为 x₁, x₂, ..., xₙ（可以是原始数据特征，也可以是其他神经元的输出）。

例如，在 MNIST 任务中，输入层神经元的输入可能是图像的像素值（0-255）。

2. 加权求和（线性变换）

每个输入信号会被赋予一个权重（Weight）w₁, w₂, ..., wₙ，权重表示该输入对神经元输出的 "重要性"（正权重表示促进作用，负权重表示抑制作用）。

神经元会计算所有输入与对应权重的乘积之和，再加上一个 "偏置项"（Bias，记为 b），得到 "加权和"（也称为 "净输入"，记为 z）：z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

偏置项的作用类似于生物神经元的 "阈值"，用于调整神经元被激活的难易程度（例如，偏置为正会降低激活门槛，偏置为负会提高门槛）。

3. 激活函数（非线性变换）

加权和 z 是一个线性结果，直接输出的话，无论多少层神经元堆叠，整个网络仍然是线性模型，无法学习复杂的非线性关系（如图像、语言中的规律）。

因此，需要对 z 应用 "激活函数"（Activation Function，记为 f），进行非线性变换，得到神经元的最终输出 y：y = f(z)

常见的激活函数有：

• ReLU：f(z) = max(0, z)（简单高效，应用最广）
• Sigmoid：f(z) = 1/(1+e⁻ᶻ)（将输出压缩到 0-1，适合二分类）
• Softmax：将多个输出转换为概率分布（适合多分类，如 MNIST 的 10 个数字）

6.1.2 神经元的作用

单个神经元可以看作一个简单的 "分类器" 或 "特征检测器"：

• 例如，在图像识别中，一个神经元可能学习 "检测边缘"（通过权重对特定像素模式敏感）；
• 在文本分类中，一个神经元可能学习 "判断是否包含负面词汇"（通过权重对负面词赋予高值）。

而多个神经元组成 "层"，层与层堆叠形成 "网络"，就能学习更复杂的特征（如从边缘到形状，再到完整物体）。

6.1.3 隐藏层

隐藏层是神经网络的 "核心学习区"：

• 定位：输入层与输出层之间的中间层，不直接与外部数据交互（"隐藏" 的由来）；
• 作用：通过多层神经元的加权计算和非线性激活，将 "低级简单特征" 逐步抽象为 "高级复杂特征"，让模型能拟合复杂数据规律；

6.2 数据准备

mnist数据官网：

https://s3.amazonaws.com/img-datasets/mnist.npz

# 导入必要的库
import numpy as np  # 导入NumPy库，用于数值计算和数组操作
from tensorflow import keras  # 导入TensorFlow的Keras接口，用于构建和训练神经网络
from keras import layers   #layers（层）是 Keras 中构建神经网络的核心组件，它包含了各种预定义的神经网络层类型，用于搭建模型的基本结构。

# 定义本地MNIST数据集的路径
local_mnist_path = "D:\\jqxx\\mnist\\keras\\datasets\\mnist.npz"

# 使用NumPy加载.npz格式的数据集文件
# allow_pickle=True允许加载包含Python对象的数组
with np.load(local_mnist_path, allow_pickle=True) as f:
    x_train = f['x_train']  # 加载训练集图像数据
    y_train = f['y_train']  # 加载训练集标签数据
    x_test = f['x_test']    # 加载测试集图像数据
    y_test = f['y_test']    # 加载测试集标签数据

# 数据预处理步骤
# 将图像数据从28x28的二维数组重塑为784个元素的一维数组（28*28=784）
# 并将像素值从整数类型（0-255）转换为浮点型，再归一化到0-1范围
x_train = x_train.reshape(60000, 784).astype("float32") / 255
x_test = x_test.reshape(10000, 784).astype("float32") / 255

# 将标签数据转换为独热编码（one-hot encoding）格式
# 因为MNIST有10个类别（0-9），所以指定num_classes=10
# 独热编码会将每个标签转换为一个长度为10的数组，只有对应类别位置为1，其余为0
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)

# 打印处理后的数据形状，验证预处理是否正确
print("训练集形状：", x_train.shape)  # 应输出(60000, 784)，表示60000个样本，每个样本784个特征
print("测试集形状：", x_test.shape)    # 应输出(10000, 784)，表示10000个样本，每个样本784个特征
print("标签形状：", y_train.shape)     # 应输出(60000, 10)，表示60000个标签，每个标签为10维独热向量

6.3 构建模型

model = keras.Sequential([
    layers.Dense(512, activation="relu", input_shape=(784,)),
    layers.Dense(10, activation="softmax")
])

keras.Sequential

• Sequential是 Keras 中最基础的模型类型，代表一个线性堆叠的神经网络层（即层与层之间依次连接，没有复杂的分支或跳跃连接），适合构建简单的神经网络。

第一层：layers.Dense(512, activation="relu", input_shape=(784,))

• Dense：全连接层（也叫密集层），表示该层中每个神经元都与上一层的所有神经元相连。

• 512：该层包含 512 个神经元（也叫隐藏单元），是一个超参数，可根据任务调整。

• activation="relu"：激活函数使用 ReLU（Rectified Linear Unit），作用是引入非线性变换，公式为max(0, x)。ReLU 能缓解梯度消失问题，加速训练，是隐藏层常用的激活函数。

• input_shape=(784,)：指定输入数据的形状。由于 MNIST 图像已被预处理为 784 维的一维向量（28×28 像素展开），因此输入形状为(784,)，表示每个样本是一个长度为 784 的向量。

  这一层是网络的输入层 + 第一个隐藏层 （因为指定了input_shape，同时包含 512 个神经元作为隐藏单元）。

为什么隐藏层需要512个神经元？

隐藏层的每个神经元都是一个 "特征检测器"（如检测图像的边缘、线条、拐角等），神经元数量越多，网络能同时学习的 "特征种类" 和 "特征细节" 就越丰富：

• 如果神经元数量太少（比如只有 10 个）：网络的 "特征容量" 不足，无法覆盖区分 10 个数字所需的所有关键特征（比如数字 "8" 的环形结构、"7" 的斜线结构），会导致欠拟合（模型在训练集和测试集上表现都差）。
• 如果神经元数量足够（比如 512 个）：网络有足够的 "冗余度" 去学习像素间的复杂关联 ------ 比如一部分神经元学习 "水平边缘"，一部分学习 "垂直边缘"，另一部分学习 "曲线组合"，最终通过这些特征的组合，精准区分不同数字。

在 MNIST 这类简单图像任务中，512 不是 "唯一正确值"，而是行业内长期实践的经验性合理值：

• 比 512 小的数值（如 128、256）：特征学习能力可能稍弱，但计算速度更快，对设备要求低；
• 比 512 大的数值（如 1024、2048）：特征学习能力可能更强，但会导致两个问题：
  • 参数量暴增（512 个神经元的隐藏层参数量为 784×512 + 512 = 402,944，1024 个则翻倍到 784×1024 + 1024 = 803,840），训练时间变长、占用内存更多；
  • 容易导致过拟合（网络学习到训练集中的噪声，比如某个手写数字的笔误，而非通用特征，测试集表现下降）。

512 恰好处于 "特征能力足够、计算成本可控、过拟合风险较低" 的平衡区间，因此成为 MNIST 任务中隐藏层神经元数量的常用选择。
输入层在哪？

输入层并没有显式地用 layers 类定义出来，而是通过隐藏层的 input_shape 参数「间接声明」的------ 这是 Keras 简化网络搭建的设计特点，需要结合网络结构逻辑来理解输入层的存在。

这里的关键是 layers.Dense(..., input_shape=(784,)) 这个参数：

• input_shape=(784,) 的含义是「告诉 Keras：这个网络的输入数据是 784 维的一维向量」。
• Keras 会根据这个参数，自动为你创建一个输入层------ 这个输入层包含 784 个神经元，每个神经元接收一个像素特征，然后将这 784 个特征完整传递给下一层（512 个神经元的隐藏层）。

3. 第二层：layers.Dense(10, activation="softmax")

• Dense：同样是全连接层，作为网络的输出层。
• 10：该层包含 10 个神经元，对应 MNIST 任务的 10 个类别（数字 0-9）。
• activation="softmax"：激活函数使用 Softmax，作用是将 10 个神经元的输出转换为概率分布 （所有输出值之和为 1），每个值表示样本属于对应类别的概率。例如，若输出为[0.1, 0.8, 0.1, ..., 0]，则模型认为该样本有 80% 概率是数字 1。

6.4 编译模型

model.compile(
    optimizer="rmsprop",
    loss="categorical_crossentropy",
    metrics=["accuracy"]
)

optimizer="rmsprop"

指定模型训练使用的优化器为 RMSprop（Root Mean Square Propagation）。优化器的作用是根据模型的损失函数值，通过反向传播更新模型参数（如权重、偏置），以最小化损失。RMSprop 是一种常用的自适应学习率优化器，能有效处理非平稳目标，在许多深度学习任务（如计算机视觉、自然语言处理）中表现良好。

loss="categorical_crossentropy"

指定损失函数为 分类交叉熵（适用于多类别分类任务）。损失函数用于衡量模型预测结果与真实标签之间的差异，是模型训练的 "目标"（需最小化）。

• categorical_crossentropy 要求标签采用 独热编码 （one-hot encoding）格式（例如，3 类分类中，标签可能为 [1,0,0] 表示第 1 类）。
• 若标签是整数格式（如 0、1、2），则应使用 sparse_categorical_crossentropy。

metrics=["accuracy"]

指定训练和评估过程中需要监控的评估指标为 准确率（Accuracy）。准确率是分类任务中最常用的指标之一，计算方式为 "预测正确的样本数 / 总样本数"。训练时，模型会在每个 epoch（轮次）结束后输出该指标，帮助判断模型性能。

6.5 训练模型

history = model.fit(
    x_train, y_train,
    batch_size=128,
    epochs=10,
    validation_split=0.2
)

model.fit()

• 这是模型训练的核心方法，用于将输入数据（x_train）和对应标签（y_train）传入模型，通过迭代优化模型参数，使模型学会从输入到输出的映射。

x_train, y_train

• x_train：训练数据集的输入特征（例如图像的像素数据、文本的向量表示等）。
• y_train：训练数据集的真实标签（与 x_train 一一对应，例如分类任务中的类别标签）。

batch_size=128

指定每次参数更新时使用的样本数量（批大小）。

• 模型训练时不会一次性使用所有数据更新参数，而是将数据分成多个批次（batch），每个批次包含 128 个样本。
• 每次迭代（batch）会计算该批次的损失，并用优化器更新一次模型参数。
• 批大小的选择会影响训练效率和模型收敛效果（需根据硬件性能和数据特点调整）

epochs=10

指定训练的总轮次（epoch）。

• 1 个 epoch 表示模型完整遍历一次所有训练数据（即所有批次的样本都被用于训练一次）。
• 这里设置为 10，意味着模型会用训练数据重复训练 10 轮，逐步优化参数以降低损失。

validation_split=0.2

指定从训练数据中划分一部分作为验证集，用于监控模型在非训练数据上的性能（避免过拟合）。

• 0.2 表示将 x_train 和 y_train 中 20% 的样本划分为验证集，剩余 80% 作为实际训练集。
• 每轮训练结束后，模型会自动在验证集上计算损失和评估指标（如之前 compile 中指定的 accuracy），帮助判断模型是否过拟合（例如训练指标变好但验证指标下降）。

history = ...

model.fit() 的返回值是一个 History 对象，其中包含训练过程中每轮的关键指标数据，例如：

• history.history['loss']：每轮训练的损失值
• history.history['accuracy']：每轮训练的准确率
• history.history['val_loss']：每轮验证的损失值
• history.history['val_accuracy']：每轮验证的准确率这些数据可用于后续绘制训练曲线，分析模型训练过程。

6.6 评估模型

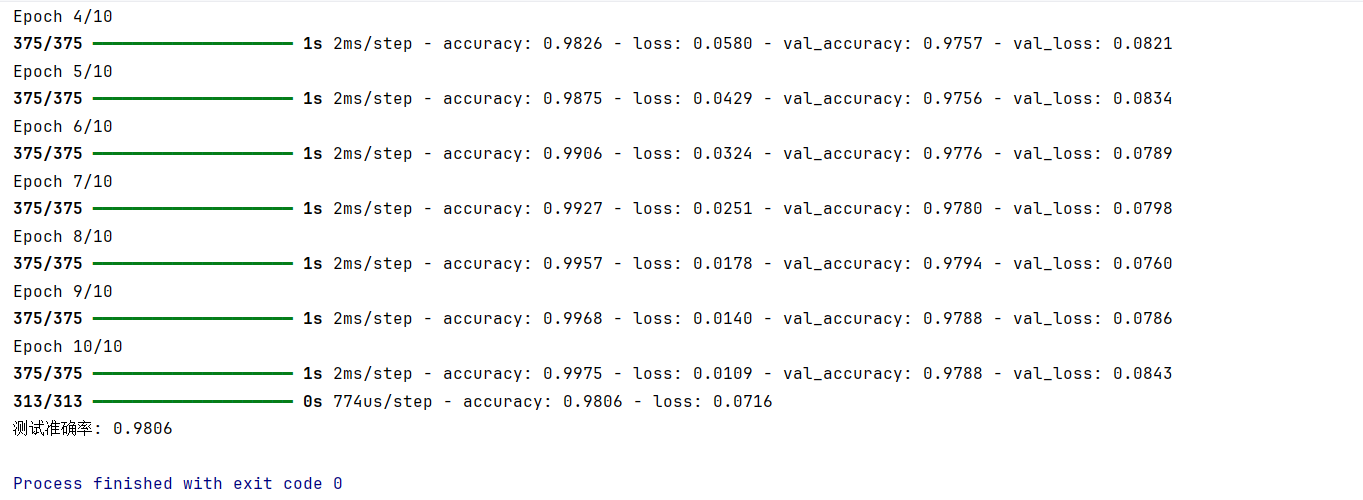
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f"测试准确率: {test_acc:.4f}")

model.evaluate(x_test, y_test)

这是模型评估的核心方法，用于在独立的测试数据集上计算模型的损失值和评估指标。

• x_test：测试数据集的输入特征（与训练时的 x_train 格式一致，但属于未参与训练的数据）。
• y_test：测试数据集的真实标签（与 x_test 一一对应，用于衡量模型预测的准确性）。该方法的返回值是一个元组，包含两个结果：
• 第一个元素是模型在测试集上的损失值 （由 model.compile 中指定的损失函数计算）。
• 第二个元素是模型在测试集上的评估指标 （这里是 compile 中指定的 accuracy，即准确率）。

test_loss, test_acc = ...

通过解构赋值，将 model.evaluate 返回的元组分别赋值给变量：

• test_loss：存储测试集上的损失值。
• test_acc：存储测试集上的准确率。

print(f"测试准确率: {test_acc:.4f}")

格式化输出测试准确率，其中 :.4f 表示保留小数点后 4 位，使结果更易读。例如，若 test_acc 为 0.892345，则输出为 测试准确率: 0.8923。