文章目录
- 1.分类(Classification)
-
- [1.1 线性分类](#1.1 线性分类)
-
- [1.1.1 简化模型](#1.1.1 简化模型)
-
- [1.1.1.1 消除阈值(Eliminating the threshold)](#1.1.1.1 消除阈值(Eliminating the threshold))
- [1.1.1.2 消除阈偏置(Eliminating the bias)](#1.1.1.2 消除阈偏置(Eliminating the bias))
- [1.1.2 线性分类的示例](#1.1.2 线性分类的示例)
- [1.1.3 二元线性分类器的总结](#1.1.3 二元线性分类器的总结)
- 2.线性回归
-
- [2.1 损失函数(loss function)](#2.1 损失函数(loss function))
-
- [2.1.1 0-1损失函数](#2.1.1 0-1损失函数)
- [2.1.2 0-1损失函数的成本函数](#2.1.2 0-1损失函数的成本函数)
- [2.1.3 0-1损失函数的优化](#2.1.3 0-1损失函数的优化)
-
- [2.1.3.1 0-1损失函数](#2.1.3.1 0-1损失函数)
- [2.1.3.2 线性回归](#2.1.3.2 线性回归)
- [2.1.3.3 逻辑激活函数(Logistic Activation Function)](#2.1.3.3 逻辑激活函数(Logistic Activation Function))
-
- [2.1.3.3.1 交叉熵损失函数(Cross-Entropy Loss)/对数损失(Log Loss)](#2.1.3.3.1 交叉熵损失函数(Cross-Entropy Loss)/对数损失(Log Loss))
- [1.2 多类分类(Multiclass Classification)和 Softmax 回归(Softmax Regression)](#1.2 多类分类(Multiclass Classification)和 Softmax 回归(Softmax Regression))
-
- [1.2.1 多类分类(Multiclass Classification)](#1.2.1 多类分类(Multiclass Classification))
- [1.2.2 Softmax 回归(Softmax Regression)](#1.2.2 Softmax 回归(Softmax Regression))
- [1.3 线性分类器的局限性](#1.3 线性分类器的局限性)
1.分类(Classification)
分类是机器学习中的一种任务,目标是预测一个离散值(discrete-valued)的目标变量。
因此二元分类(Binary Classification)是分类问题的一个子集,目标是预测一个二元值(binary-valued)的目标变量,即只有两个可能的类别。
例如:
- 疾病诊断:给定患者各种症状的存在或缺失,预测患者是否患有某种疾病。
- 垃圾邮件分类:将电子邮件分类为垃圾邮件或非垃圾邮件。
- 欺诈检测:预测金融交易是否为欺诈行为。
而多类分类(Multiclass Classification)是另一种分类问题,目标是预测一个有多个离散值(超过两个类别)的目标变量。
1.1 线性分类
我们给出详细的定义。
分类是一种监督学习任务,给定一个 D-维的输入 x ∈ R D \mathbf{x} \in \mathbb{R}^D x∈RD,目标是预测一个离散值的目标变量。
二元分类是分类问题的一个子集,目标是预测一个二元值(binary-valued)的目标变量 t t t,即 t ∈ { 0 , 1 } t∈\{0,1\} t∈{0,1}。
训练样本中,目标变量 t = 1 t=1 t=1的样本称为正例(positive examples),目标变量 t=0 的样本称为负例(negative examples)。
为了方便计算,有时会使用 t ∈ { − 1 , + 1 } t∈\{−1,+1\} t∈{−1,+1}来表示二元目标变量。
在二元线性分类中,模型的预测 y y y是输入 x x x的线性函数,然后通过一个阈值 r r r进行分类:
z = w ⊤ x + b z = \mathbf{w}^\top \mathbf{x} + b z=w⊤x+b
y = { 1 if z ≥ r 0 if z < r y = \begin{cases} 1 & \text{if } z \geq r \\ 0 & \text{if } z < r \end{cases} y={10if z≥rif z<r
其中, w \mathbf{w} w是权重向量, b b b是偏置项, z z z是线性函数的输出, r r r是分类阈值。
1.1.1 简化模型
在二元线性分类中简化模型有两种方法:消除阈值和消除偏置项。
1.1.1.1 消除阈值(Eliminating the threshold)
我们可以假设(在不损失一般性的情况下,即WLOG)阈值 r = 0 r=0 r=0。
因此源氏的分类条件就可以进行转化。
w ⊤ x + b ≥ r ⟺ w ⊤ x + b − r ≥ 0 \mathbf{w}^\top \mathbf{x} + b \geq r \iff \mathbf{w}^\top \mathbf{x} + b - r \geq 0 w⊤x+b≥r⟺w⊤x+b−r≥0
由于 r = 0 r=0 r=0,这个条件进一步简化。
w ⊤ x + b ≥ 0 \mathbf{w}^\top \mathbf{x} + b \geq 0 w⊤x+b≥0
这里我们将 w 0 w_0 w0定义为 b b b,即 w 0 ≜ b w_0 \triangleq b w0≜b。
1.1.1.2 消除阈偏置(Eliminating the bias)
添加一个总是取值为1的虚拟特征 x 0 x_0 x0 。这样,权重 w 0 = b w_0=b w0=b就相当于偏置项(与线性回归中的偏置相同)。
因此现在我们可以简化模型为:
输入:接受输入 x ∈ R D + 1 \mathbf{x} \in \mathbb{R}^{D+1} x∈RD+1,其中 x 0 = 1 x_0=1 x0=1。
线性函数:计算 z = w ⊤ x z=\mathbf{w}^\top \mathbf{x} z=w⊤x
因此我们根据 z z z的值进行分类:
y = { 1 if z ≥ 0 0 if z < 0 y = \begin{cases} 1 & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases} y={10if z≥0if z<0
1.1.2 线性分类的示例
在学习初期,我们会介绍简单的示例,专注于最小化训练集误差并暂时忽略泛化能力。
例1:逻辑运算NOT。
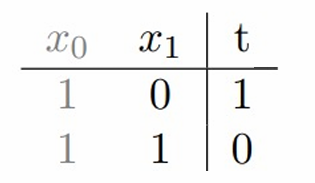
这里输入的数据会接受特征,如果特征相同,那其标签就为0,否则就为1。
为了实现完美分类,需要找到合适的权重 w 0 w_0 w0和 w 1 w_1 w1,使得对于所有特征,模型的预测 z = w 0 x 0 + w 1 x 1 z=w_0x_0+w_1x_1 z=w0x0+w1x1与真实标签 t t t一致。
按照上表的这几个样本我们可以得到:
当 x 1 = 0 x_1=0 x1=0时,需要 z = w 0 ≥ 0 z=w_0≥0 z=w0≥0以确保分类正确,这意味着 w 0 w_0 w0必须非负。
当 x 1 = 1 x_1=1 x1=1时,需要 z = w 0 + w 1 < 0 z=w_0+w_1<0 z=w0+w1<0以确保分类正确,这意味着 w 0 + w 1 w_0+w_1 w0+w1必须为负。
对于这个例子, w 0 = 1 , w 1 = − 2 w_0=1,w_1=-2 w0=1,w1=−2就是可以满足的一个解,当然满足的解有很多。
例2:逻辑运算AND。
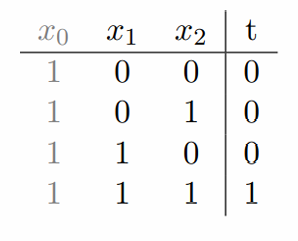
对于现在这个例子,那我们现在的预测 z = w 0 x 0 + w 1 x 1 + w 2 x 2 z=w_0x_0+w_1x_1+w_2x_2 z=w0x0+w1x1+w2x2
按照上表的这几个样本我们可以得到:
w 0 < 0 w_0<0 w0<0
w 0 + w 2 < 0 w_0+w_2<0 w0+w2<0
w 0 + w 1 < 0 w_0+w_1<0 w0+w1<0
w 0 + w 1 + w 2 ≥ 0 w_0+w_1+w_2≥0 w0+w1+w2≥0
这里给出一个可行的解: w 0 = − 1.5 , w 1 = 1 , w 2 = 1 w_0=-1.5,w_1=1,w_2=1 w0=−1.5,w1=1,w2=1
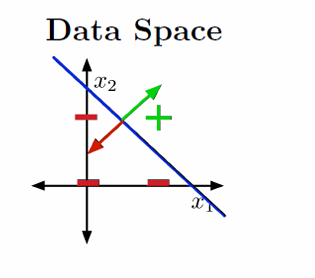
我们尝试用几何图来展示刚刚的两个例子。
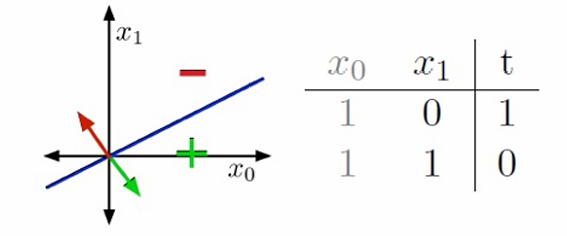
图中展示了输入空间(也称为数据空间),其中 x 0 x_0 x0和 x 1 x_1 x1是特征轴,代表数据的两个维度。训练样本在输入空间中表示为点。
权重向量 w \mathbf{w} w定义了两个半空间:
H + = { x : w ⊤ x ≥ 0 } H_+ = \{ \mathbf{x} : \mathbf{w}^\top \mathbf{x} \geq 0 \} H+={x:w⊤x≥0} :正半空间,其中所有点的线性组合 w ⊤ x ≥ 0 \mathbf{w}^\top \mathbf{x} \geq 0 w⊤x≥0
H − = { x : w ⊤ x < 0 } H_- = \{ \mathbf{x} : \mathbf{w}^\top \mathbf{x} < 0 \} H−={x:w⊤x<0}负半空间,其中所有点的线性组合 w ⊤ x < 0 \mathbf{w}^\top \mathbf{x} < 0 w⊤x<0
决策边界是 w ⊤ x = 0 \mathbf{w}^\top \mathbf{x} = 0 w⊤x=0的集合,它将输入空间分为两个区域。
在二维空间(2-D)中,决策边界是一条直线;在更高维度中,它是超平面。
如果训练样本可以通过一个线性决策规则完美分开,那么我们说数据是线性可分的(linear separable)。这意味着存在一个权重向量 w \mathbf{w} w,使得所有正例和负例分别位于决策边界的两侧。
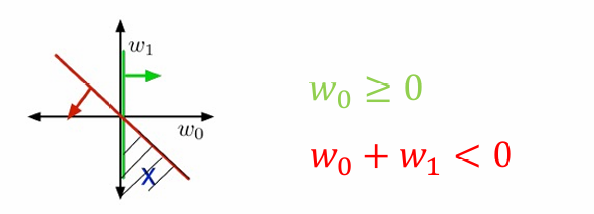
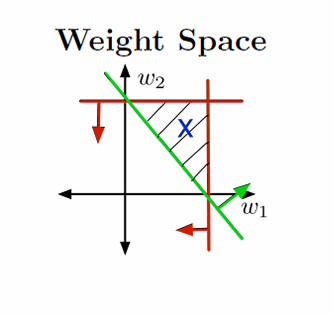
图片展示了权重空间(Weight Space)。
在权重空间中,权重向量 w \mathbf{w} w被视为点。
每个训练样本 x x x指定了一个半空间,权重向量 w \mathbf{w} w必须位于这个半空间内,以便正确分类该样本:
如果 t = 1 t=1 t=1,则需要 w ⊤ x ≥ 0 \mathbf{w}^\top \mathbf{x} \geq 0 w⊤x≥0。
如果 t = 0 t=0 t=0,则需要 w ⊤ x < 0 \mathbf{w}^\top \mathbf{x} < 0 w⊤x<0。
满足所有约束条件的区域称为可行区域(feasible region)。
如果这个区域不为空,则问题是可行的(feasible);如果这个区域为空,则问题是不可行的(infeasible)。
这里红线和绿线之间的阴影部分代表了可行解的范围,也就是可行区域(feasible region)。
在例2中,由于是三维空间,其中包括一个虚拟维度(dummy dimension),通常用于表示偏置项(bias)。所以为了可视化三维数据空间和权重空间,我们可以查看一个二维切片(slice)。
无论在数据空间还是权重空间中,可视化的结果都是相似的。满足所有约束条件的可行集(feasible set)总是有一个角在原点(origin)。这是因为当所有权重都为零时,模型不会对任何输入产生影响,这通常满足所有分类约束。
这里选择 x 0 = 1 x_0=1 x0=1进行切片。
示例解如 w 0 = − 1.5 , w 1 = 1 , w 2 = 1 w_0=-1.5,w_1=1,w_2=1 w0=−1.5,w1=1,w2=1。
决策边界的方程是 w 0 x 0 + w 1 x 1 + w 2 x 2 = 0 w_0x_0+w_1x_1+w_2x_2=0 w0x0+w1x1+w2x2=0,代入示例解得到 − 1.5 + x 1 + x 2 = 0 -1.5+x_1+x_2=0 −1.5+x1+x2=0。
这里选择 w 0 = − 1.5 w_0=-1.5 w0=−1.5进行切片。
约束条件为 w 0 < 0 , w 0 + w 2 < 0 , w 0 + w 1 < 0 , w 0 + w 1 + w 2 ≥ 0 w_0<0,w_0+w_2<0,w_0+w_1<0,w_0+w_1+w_2≥0 w0<0,w0+w2<0,w0+w1<0,w0+w1+w2≥0
同理这里阴影部分代表了可行解的范围。
1.1.3 二元线性分类器的总结
目标变量 t t t取值为 { 0 , 1 } \{0,1\} {0,1}。
输入向量 x ∈ R D + 1 \mathbf{x} \in \mathbb{R}^{D+1} x∈RD+1,其中 x 0 = 1 x_0=1 x0=1是一个虚拟特征,用于表示偏置项。
模型由权重向量 w \mathbf{w} w定义,预测 y y y是输入 x x x的线性函数,然后通过阈值进行分类: z = w ⊤ x z = \mathbf{w}^\top \mathbf{x} z=w⊤x
y = { 1 if z ≥ 0 0 if z < 0 y = \begin{cases} 1 & \text{if } z \geq 0 \\ 0 & \text{if } z < 0 \end{cases} y={10if z≥0if z<0
如果训练集是线性可分的,我们可以使用线性规划来求解权重 w。
也可以使用感知机算法(perceptron algorithm),这是一种迭代过程,但主要是出于历史兴趣。
如果数据不是线性可分的,问题会变得更加困难。
在现实生活中,数据几乎从不具有线性可分性。
2.线性回归
2.1 损失函数(loss function)
在机器学习模型的训练过程中,我们首先需要定义一个损失函数(loss function),用于量化模型预测值与实际值之间的差异。
然后最小化小化这个损失函数在整个训练集上的平均值(或总和),这个平均值(或总和)被称为成本函数(cost function)。
2.1.1 0-1损失函数
0-1损失函数是一种看似直观的损失函数,其定义如下:
L 0 − 1 ( y , t ) = { 0 if y = t 1 if y ≠ t \mathcal{L}_{0-1}(y, t) = \begin{cases} 0 & \text{if } y = t \\ 1 & \text{if } y \neq t \end{cases} L0−1(y,t)={01if y=tif y=t
其中, y y y是模型的预测值, t t t是真实值。如果预测值与真实值相等,损失为0;否则,损失为1。
也可以用指示函数(indicator function)表示为 L 0 − 1 ( y , t ) = I [ y ≠ t ] \mathcal{L}_{0-1}(y, t) = \mathbb{I}[y \neq t] L0−1(y,t)=I[y=t],其中 I \mathbb{I} I是指示函数。
2.1.2 0-1损失函数的成本函数
成本函数是训练样本上损失的平均值(或总和)。对于0-1损失,成本函数实际上就是错误分类率(misclassification rate),即训练集中被错误分类的样本比例。因此公式为: J = 1 N ∑ i = 1 N I [ y ( i ) ≠ t ( i ) ] \mathcal{J} = \frac{1}{N} \sum_{i=1}^{N} \mathbb{I}[y^{(i)} \neq t^{(i)}] J=N1∑i=1NI[y(i)=t(i)]。
2.1.3 0-1损失函数的优化
2.1.3.1 0-1损失函数
因此我们现在要尝试优化0-1损失函数,但这个问题可能是NP难(NP-hard)问题。因为0-1损失函数是一个阶梯函数(step function),它在预测正确和错误之间有一个突然的变化。这种函数不是"良好"的,因为它不满足一些优化算法所需的性质,如连续性(continuity)、平滑性(smoothness)和凸性(convexity)。由于这些性质的缺失,常见的优化算法(如梯度下降)可能无法有效地应用于0-1损失函数。
我们现在使用链式法则计算0-1损失函数关于权重 w j w_j wj的偏导数: ∂ L 0 − 1 ∂ w j = ∂ L 0 − 1 ∂ z ⋅ ∂ z ∂ w j \frac{\partial \mathcal{L}{0-1}}{\partial w_j} = \frac{\partial \mathcal{L}{0-1}}{\partial z} \cdot \frac{\partial z}{\partial w_j} ∂wj∂L0−1=∂z∂L0−1⋅∂wj∂z
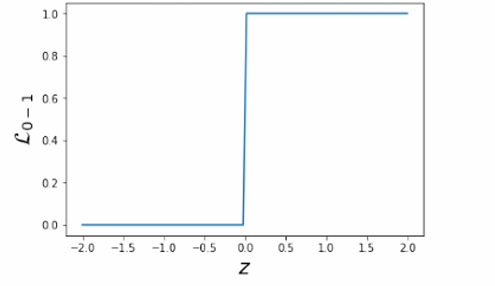
我们会发现这个导数在定义域内处处为零,因为0-1损失函数是一个阶梯函数,没有平滑的过渡。
∂ L 0 − 1 ∂ z = 0 \frac{\partial \mathcal{L}_{0-1}}{\partial z} = 0 ∂z∂L0−1=0 意味着微小地改变权重对损失几乎没有影响。
几乎任何点的梯度都是零,这意味着无法使用基于梯度的优化算法(如梯度下降)来找到损失函数的最小值。
2.1.3.2 线性回归
我们现在尝试使用使用线性回归来替代原始损失函数来进行优化。我们这种方法被称为使用平滑替代损失函数的松弛(relaxation)。
与其基于最终预测结果定义损失,不如直接基于模型的中间输出 z z z来定义损失。这里 z z z是模型的线性组合输出,即 z = w ⊤ x z=\mathbf{w}^\top \mathbf{x} z=w⊤x。
由于我们已经知道如何拟合线性回归模型,我们可以考虑使用平方误差损失函数(Squared Error Loss, SE)来衡量预测值 z z z与真实标签 t t t之间的差异: L SE ( z , t ) = 1 2 ( z − t ) 2 \mathcal{L}_{\text{SE}}(z, t) = \frac{1}{2}(z - t)^2 LSE(z,t)=21(z−t)2
尽管目标变量实际上是二元的(0或1),我们可以将其视为连续值进行处理。
对于这个损失函数,通过在 1 2 \frac{1}{2} 21处对 z z z进行阈值处理来进行最终预测是有意义的。这是因为平方误差损失函数在 z = t z=t z=t时达到最小值,而在二元分类的上下文中, t t t通常取值为0或1。因此,将 z z z阈值化在0.5处,可以有效地将连续的预测值 z z z转换为二元预测。
这种方法也有问题,如下图所示。
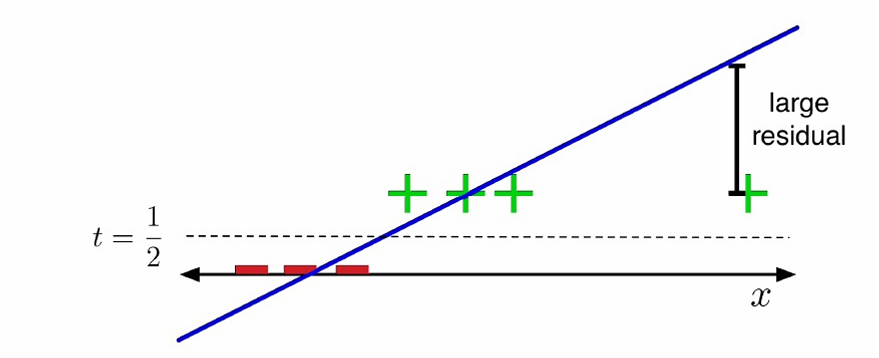
图中展示了一个线性决策边界。
损失函数"不喜欢"高置信度的正确预测。这是因为平方误差损失函数对所有误差赋予相同的权重,无论预测值与真实值之间的差距有多大。
例如,如果 t = 1 t=1 t=1,模型预测 z = 10 z=10 z=10比预测 z = 0 z=0 z=0更糟糕,因为 z = 10 z=10 z=10与真实值 t = 1 t=1 t=1之间的差距更大,导致平方误差更大。
2.1.3.3 逻辑激活函数(Logistic Activation Function)
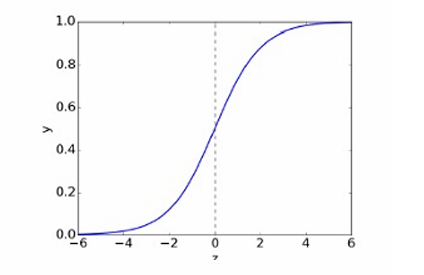
逻辑激活函数(Logistic Activation Function),也称为sigmoid函数,它在二元分类问题中用于将线性模型的输出映射到0和1之间的概率值。
没有理由预测超出[0, 1]区间的值,因此需要将输出值压缩到这个区间内。
逻辑函数是一种S形函数(sigmoid function),其定义为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
这个函数将任何实数 z z z映射到0和1之间。
σ − 1 ( y ) = log ( y 1 − y ) \sigma^{-1}(y) = \log\left(\frac{y}{1 - y}\right) σ−1(y)=log(1−yy)被称为logit,它是逻辑函数的逆函数。
将线性模型与逻辑非线性函数结合,称为逻辑线性模型(Log-linear Model:
z = w ⊤ x z = \mathbf{w}^\top \mathbf{x} z=w⊤x
y = σ ( z ) y = \sigma(z) y=σ(z)
这里, z z z是线性组合的输出, y y y是通过逻辑函数映射后的概率输出。
使用平方误差损失函数来衡量预测值 y y y与真实标签 t 之间的差异:
L SE ( y , t ) = 1 2 ( y − t ) 2 \mathcal{L}_{\text{SE}}(y, t) = \frac{1}{2}(y - t)^2 LSE(y,t)=21(y−t)2
在这种用法中, σ \sigma σ被称为激活函数(activation function)。
在使用逻辑激活函数时,当预测值 z z z远离真实标签时,可能会出现梯度消失问题。
下图展示了平方误差损失函数 L S E \mathcal{L}_{SE} LSE作为 z z z的函数的图,假设真实标签 t = 1 t=1 t=1。
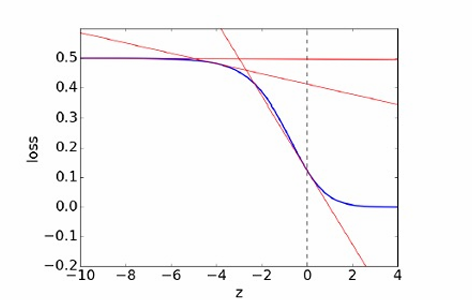
损失函数关于权重 w j w_j wj的导数为 ∂ L ∂ w j = ∂ L ∂ z ⋅ ∂ z ∂ w j \frac{\partial \mathcal{L}}{\partial w_j} = \frac{\partial \mathcal{L}}{\partial z} \cdot \frac{\partial z}{\partial w_j} ∂wj∂L=∂z∂L⋅∂wj∂z
当 z ≪ 0 z≪0 z≪0时,逻辑激活函数 σ ( z ) ≈ 0 σ(z)≈0 σ(z)≈0。
损失函数关于 z z z的导数 ∂ L ∂ z ≈ 0 \frac{\partial \mathcal{L}}{\partial z} \approx 0 ∂z∂L≈0,因此 ∂ L ∂ w j ≈ 0 \frac{\partial \mathcal{L}}{\partial w_j} \approx 0 ∂wj∂L≈0。这意味着权重 w j w_j wj的梯度很小,导致权重更新很小,权重 w j w_j wj像是一个临界点。
如果预测结果与真实标签相差很大(即 z z z远离0),那么模型应该远离临界点(即候选解)。
2.1.3.3.1 交叉熵损失函数(Cross-Entropy Loss)/对数损失(Log Loss)
逻辑回归模型输出 y y y属于区间 [0, 1],可以解释为 t = 1 t=1 t=1的估计概率。如果 t = 0 t=0 t=0,则希望对接近 1 的 y y y进行重罚。
交叉熵损失函数捕捉了这种直觉,其定义如下:
L CE ( y , t ) = { − log y if t = 1 − log ( 1 − y ) if t = 0 \mathcal{L}_{\text{CE}}(y, t) = \begin{cases} -\log y & \text{if } t = 1 \\ -\log(1 - y) & \text{if } t = 0 \end{cases} LCE(y,t)={−logy−log(1−y)if t=1if t=0
这可以简化为: L CE ( y , t ) = − t log y − ( 1 − t ) log ( 1 − y ) \mathcal{L}_{\text{CE}}(y, t) = -t \log y - (1 - t) \log(1 - y) LCE(y,t)=−tlogy−(1−t)log(1−y)
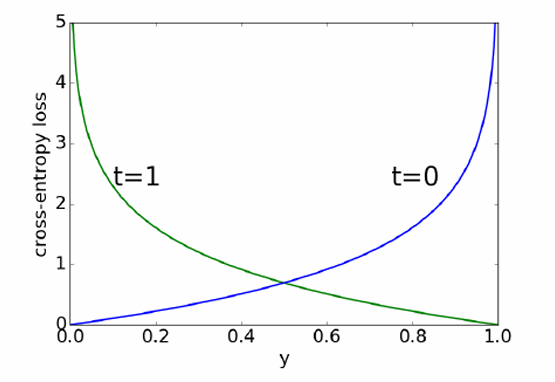
当 t = 1 t=1 t=1时,如果模型预测 y y y接近 1,损失较小;如果 y y y远离 1,损失较大。
当 t = 0 t=0 t=0时,如果模型预测 y y y接近 0,损失较小;如果 y y y远离 0,损失较大。
下图展示了当目标 t = 1 t=1 t=1时,交叉熵损失函数关于 z z z的图形。
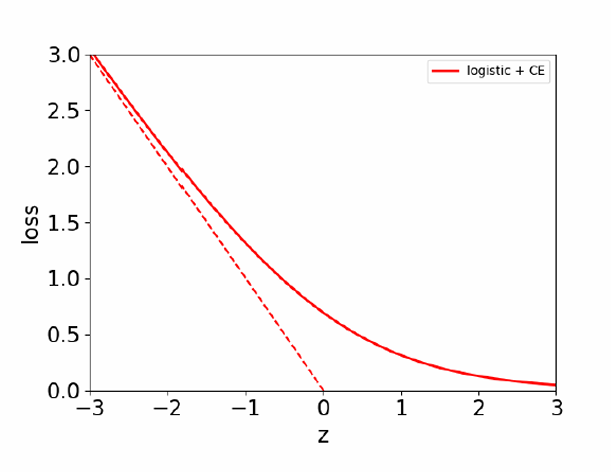
图中实线表示逻辑回归模型的损失,虚线表示线性回归模型的损失(平方误差损失)。
可以看到,当 z z z值较大(即模型对正例的预测置信度较高)时,逻辑回归的损失较小,这与交叉熵损失函数的特性相符。
现在我们可以使用梯度下降法来最小化逻辑回归(Logistic Regression)的成本函数 J \mathcal{J} J。逻辑损失函数在权重 w w w上是凸函数(convex function)。凸函数的一个重要性质是它们有一个全局最小值。
标准的权重初始化是将权重 w w w设置为零。这样做的原因包括:
- 零初始化简单且计算方便。
- 它可以防止某些特征在训练初期对损失函数的影响过大,从而有助于模型的稳定训练。
- 在某些情况下,非零初始化可能导致梯度消失或梯度爆炸问题,这些问题会阻碍模型的学习过程。
首先交叉熵损失函数的定义为:
L CE ( y , t ) = − t log y − ( 1 − t ) log ( 1 − y ) \mathcal{L}_{\text{CE}}(y, t) = -t \log y - (1 - t) \log(1 - y) LCE(y,t)=−tlogy−(1−t)log(1−y)这里, y y y是模型预测的概率, t t t是真实标签。
逻辑函数 y y y定义为: y = 1 1 + e − z y = \frac{1}{1 + e^{-z}} y=1+e−z1。其中, z = w ⊤ x z = \mathbf{w}^\top \mathbf{x} z=w⊤x是线性组合的输出。
根据链式法则: ∂ L CE ∂ w j = ( − t y + 1 − t 1 − y ) ⋅ y ( 1 − y ) ⋅ x j = ( y − t ) x j \frac{\partial \mathcal{L}_{\text{CE}}}{\partial w_j} = \left(-\frac{t}{y} + \frac{1 - t}{1 - y}\right) \cdot y(1 - y) \cdot x_j = (y - t)x_j ∂wj∂LCE=(−yt+1−y1−t)⋅y(1−y)⋅xj=(y−t)xj
梯度下降(coordinate-wise)更新规则用于找到逻辑回归的权重:
w j ← w j − α ∂ J ∂ w j w_j \leftarrow w_j - \alpha \frac{\partial \mathcal{J}}{\partial w_j} wj←wj−α∂wj∂J
= w j − α N ∑ i = 1 N ( y ( i ) − t ( i ) ) x j ( i ) = w_j - \frac{\alpha}{N} \sum_{i=1}^{N} (y^{(i)} - t^{(i)}) x_j^{(i)} =wj−Nα∑i=1N(y(i)−t(i))xj(i)
这里, α α α是学习率, N N N是样本数量。
我们可以注意到线性回归和逻辑回归的梯度下降更新规则都为:
w ← w − α N ∑ i = 1 N ( y ( i ) − t ( i ) ) x ( i ) \mathbf{w} \leftarrow \mathbf{w} - \frac{\alpha}{N} \sum_{i=1}^{N} (y^{(i)} - t^{(i)}) \mathbf{x}^{(i)} w←w−Nα∑i=1N(y(i)−t(i))x(i)
它们都是广义线性模型(generalized linear models)的例子。
注意到求和符号前的 1 N \frac{1}{N} N1,这是由于损失是平均计算的。当损失是求和而不是平均值时,需要较小的学习率 α ′ = α N \alpha' = \frac{\alpha}{N} α′=Nα
1.2 多类分类(Multiclass Classification)和 Softmax 回归(Softmax Regression)
1.2.1 多类分类(Multiclass Classification)
前面我们说的是二元分类,现在我们将注意力放在多类分类上,我们现在的目标是预测一个大于两个类别的离散值目标变量。
例如:1.手写数字识别:预测手写数字的值,例如,识别手写数字0到9。

2.邮件分类:将电子邮件分类为不同的类别,如垃圾邮件、旅行邮件、工作邮件、个人邮件等。

在多类分类问题中,目标变量(targets)形成一个离散集合 { 1 , ⋯ , K } \{1,⋯,K\} {1,⋯,K},其中 K K K表示类别的总数。
我们可以使用独热向量表示多类标签法,它将每个类别编码为一个长度为 K K K的向量,其中只有一个位置是1,其余位置都是0。
t = ( 0 , ⋯ , 0 , 1 , 0 ⋯ , 0 ) ∈ R K t = (0, \cdots, 0, 1, 0 \cdots, 0) \in \mathbb{R}^K t=(0,⋯,0,1,0⋯,0)∈RK
这里, t ∈ R K t ∈ \mathbb{R}^K t∈RK表示向量 t t t是一个 K K K维实数向量,其中第 k k k个位置是1,其余位置都是0。
对于每个类别 k k k,线性函数可以表示为: z k = ∑ j = 1 D w k j x j + b k for k = 1 , 2 , ⋯ , K z_k = \sum_{j=1}^{D} w_{kj} x_j + b_k \quad \text{for } k = 1, 2, \cdots, K zk=∑j=1Dwkjxj+bkfor k=1,2,⋯,K
这里, z k z_k zk是第 k k k类的线性组合输出, w k j w_{kj} wkj是权重, x j x_j xj是输入特征, b k b_k bk是偏置项, D D D是输入维度的数量, K K K是输出类别的数量。
可以通过将权重矩阵 W \mathbf{W} W扩展到 R K × ( D + 1 ) \mathbb{R}^{K×(D+1)} RK×(D+1)并添加一个虚拟变量 x 0 = 1 x_0=1 x0=1来消除偏置 b b b。
这样,线性函数可以向量化表示为: z = W x + b \mathbf{z} = \mathbf{W} \mathbf{x} + \mathbf{b} z=Wx+b
这里权重 W \mathbf{W} W是一个 K × D K×D K×D的矩阵,其中每一行对应一个类别的权重。偏置 b b b是一个 K K K维向量,其中每个元素对应一个类别的偏置。
其中, z \mathbf{z} z是 K K K维的输出向量, W \mathbf{W} W是扩展后的权重矩阵, x x x是扩展后的输入向量。
向量化表示,添加虚拟变量 x 0 = 1 x_0=1 x0=1: z = W x \mathbf{z} = \mathbf{W} \mathbf{x} z=Wx
那么现在如何将线性预测转换为独热编码(one-hot encoding)的预测呢?
我们可以将 z k z_k zk的大小解释为模型偏好类别 k k k作为其预测的程度的度量。
如果我们这样做,我们应该设置预测值 y i y_i yi为 y i = { 1 if i = arg max k z k 0 otherwise y_i = \begin{cases} 1 & \text{if } i = \arg\max_k z_k \\ 0 & \text{otherwise} \end{cases} yi={10if i=argmaxkzkotherwise
这里 arg max k z k \arg\max_k z_k argmaxkzk表示选择 z k z_k zk中最大的索引 i i i,即模型最偏好的类别。
1.2.2 Softmax 回归(Softmax Regression)
我们需要"软化"我们的预测,以便进行优化。这里会使用 Softmax 回归。这意味着我们希望模型的输出更平滑,而不是像0-1损失函数那样在正确和错误预测之间有突然的变化。
我们希望模型的输出像概率一样"软",即 0 ≤ y k ≤ 1 0≤y_k≤1 0≤yk≤1并且所有输出的和为1。
一个自然的激活函数选择是Softmax函数,它是逻辑函数的多变量推广。Softmax函数定义为: y k = softmax ( z 1 , ⋯ , z K ) k = e z k ∑ k ′ e z k ′ y_k = \text{softmax}(z_1, \cdots, z_K)k = \frac{e^{z_k}}{\sum{k'} e^{z_{k'}}} yk=softmax(z1,⋯,zK)k=∑k′ezk′ezk这里, z k z_k zk是第 k k k类的线性组合输出, y k y_k yk是第 k k k类的预测概率。
输出可以解释为概率(正值且和为1)。如果 z k z_k zk远大于其他值,则 s o f t m a x ( z ) k ≈ 1 softmax(z)_k≈1 softmax(z)k≈1,Softmax函数表现得像argmax(选择最大值的函数)。
和前面类似,我们可以使用交叉熵损失函数作为损失函数。交叉熵损失函数定义为: L CE ( y , t ) = − ∑ k = 1 K t k log y k \mathcal{L}{\text{CE}}(\mathbf{y}, \mathbf{t}) = - \sum{k=1}^{K} t_k \log y_k LCE(y,t)=−∑k=1Ktklogyk
这里, y y y是模型输出的概率向量, t t t是真实标签的独热编码向量, K K K是类别的数量, t k t_k tk和 y k y_k yk分别是第 k k k类的真实标签和预测概率。
交叉熵损失函数也可以表示为向量形式: L CE = − t ⊤ ( log y ) , \mathcal{L}_{\text{CE}}= - \mathbf{t}^\top (\log \mathbf{y}), LCE=−t⊤(logy),
通常,Softmax函数和交叉熵损失结合在一起使用,形成Softmax-交叉熵损失函数。这种组合允许模型输出类别概率,并使用交叉熵损失来衡量预测概率与真实标签之间的差异。
因此Softmax回归的更新规则与线性回归和逻辑回归的更新规则相似。
Softmax回归模型:线性组合的输出 z z z计算为: z = W x z = \mathbf{W} \mathbf{x} z=Wx
然后通过Softmax函数转换为预测概率 y y y: y = softmax ( z ) y = \text{softmax}(z) y=softmax(z)
交叉熵损失函数定义为: L CE = − t ⊤ ( log y ) \mathcal{L}_{\text{CE}} = -\mathbf{t}^\top (\log \mathbf{y}) LCE=−t⊤(logy)
梯度下降更新规则用于更新权重矩阵 W \mathbf{W} W的每一行: ∂ L CE ∂ w k = ∂ L CE ∂ z k ⋅ ∂ z k ∂ w k = ( y k − t k ) ⋅ x \frac{\partial \mathcal{L}_{\text{CE}}}{\partial \mathbf{w}k} = \frac{\partial \mathcal{L}{\text{CE}}}{\partial z_k} \cdot \frac{\partial z_k}{\partial \mathbf{w}_k} = (y_k - t_k) \cdot \mathbf{x} ∂wk∂LCE=∂zk∂LCE⋅∂wk∂zk=(yk−tk)⋅x,其中, y k y_k yk是第 k k k类的预测概率, t k t_k tk是第 k k k类的真实标签, x x x是输入特征向量。
权重更新公式为: w k ← w k − α 1 N ∑ i = 1 N ( y k ( i ) − t k ( i ) ) x ( i ) \mathbf{w}_k \leftarrow \mathbf{w}k - \alpha \frac{1}{N} \sum{i=1}^{N} (y_k^{(i)} - t_k^{(i)}) \mathbf{x}^{(i)} wk←wk−αN1∑i=1N(yk(i)−tk(i))x(i)
这里的这些相似性表明这些方法在数学形式上具有一定的共通性。
1.3 线性分类器的局限性
线性分类器,如感知机或线性支持向量机(SVM),假设数据可以通过线性决策边界来分离。然而,并非所有数据集都能用直线(或超平面)来分离。
例如逻辑运算符异或(XOR)问题就是一个非线性可分数据集的一个例子。
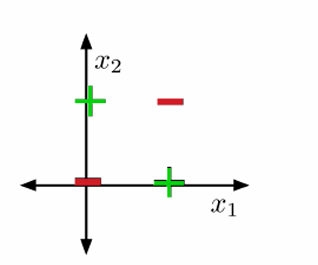
我们可以使用反证法来证明XOR问题不是线性可分的。
假设存在一组权重( w \mathbf{w} w)能够将XOR问题的数据集线性分开。
如果正例(绿色点)位于正半空间,则连接这些点的线段也必须位于正半空间。
同理,负例(红色点)必须位于负半空间。
然而,连接正例和负例的线段的交点不能同时位于两个半空间,这产生了矛盾。
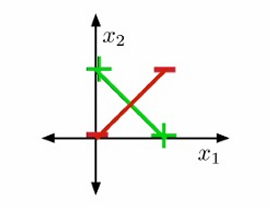
但是我们可以通过手工构造新的特征(feature map)让它变得线性可分。
我们定义三个新特征(即把二维点映射到三维空间): ϕ ( x ) = ( x 1 , x 2 , x 1 x 2 ) ⊤ \phi(\mathbf{x}) = \bigl(x_1,\; x_2,\; x_1 x_2\bigr)^{\!\top} ϕ(x)=(x1,x2,x1x2)⊤

这样我们就可以找到一张超平面把四类点完美分开。