深入理解RNN及其变体：从传统RNN到LSTM、GRU（附PyTorch实战）

本文带你系统掌握循环神经网络（RNN）的核心原理，深入剖析其三大经典变体------LSTM、Bi-LSTM、GRU 和 Bi-GRU 的内部机制，并结合 PyTorch 实战代码讲解实现细节。全文图文并茂、由浅入深，助你彻底搞懂序列建模的基础模型！

引言：为什么我们需要RNN？

在自然语言处理（NLP）、语音识别、时间序列预测等领域中，数据往往具有时序性或序列结构特征。例如一句话中的词是有顺序的，前一个词会影响后一个词的理解。

传统的全连接神经网络和卷积神经网络（CNN）无法有效捕捉这种长期依赖关系，因为它们假设输入之间是独立的。

而 循环神经网络（Recurrent Neural Network, RNN） 正是为了处理这类序列数据而生。它通过"记忆"历史信息，在每个时间步更新隐藏状态，从而建模序列间的动态变化。

然而，标准RNN存在严重的梯度消失/爆炸问题 ，难以学习长距离依赖。为此，研究者提出了更强大的变体：LSTM 和 GRU。

本篇文章将带你：

理解RNN的基本结构与工作原理
掌握LSTM和GRU如何解决长程依赖问题
学习双向结构（Bi-LSTM/Bi-GRU）的优势
使用PyTorch动手搭建各类RNN模型
分析各模型的优缺点及适用场景

一、什么是RNN？基本结构与工作机制

1.1 RNN概述

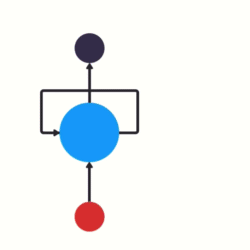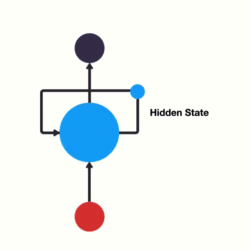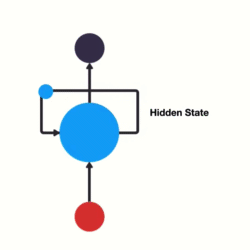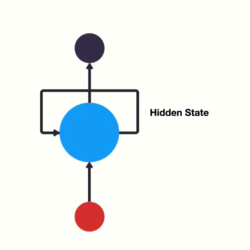
RNN（Recurrent Neural Network） 是一类专为处理序列数据 设计的神经网络。它的核心思想是：利用上一时刻的输出作为当前时刻的输入之一，形成"循环"结构，从而保留对过去信息的记忆。

数学表达式如下：
ht=tanh⁡(Whhht−1+Wxhxt+bh) h_t = \tanh(W_{hh} h_{t-1} + W_{xh} x_t + b_h) ht=tanh(Whhht−1+Wxhxt+bh)

其中：

xtx_txt：第ttt个时间步的输入
ht−1h_{t-1}ht−1：上一时间步的隐藏状态（即"记忆"）
hth_tht：当前时间步的隐藏状态
Whh,WxhW_{hh}, W_{xh}Whh,Wxh：可训练权重矩阵

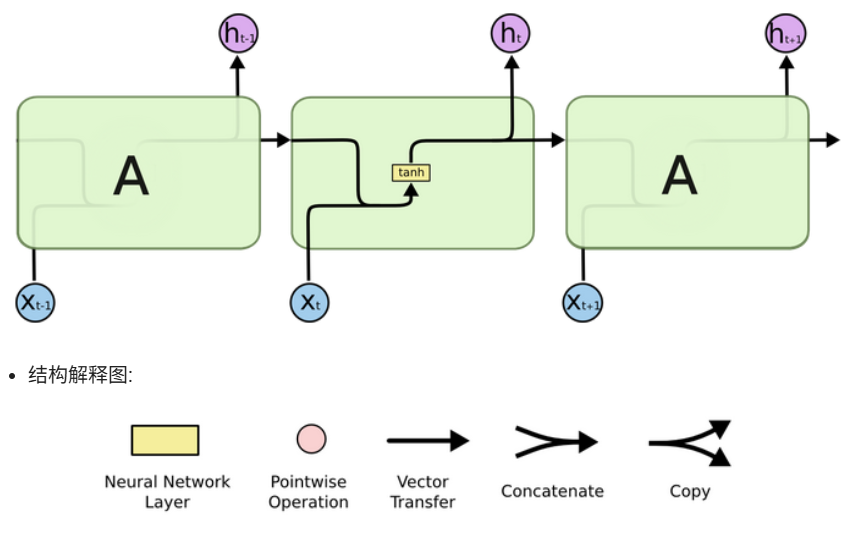
这个hth_tht既是当前输出的一部分，也会传给下一个时间步，构成了"循环"。

1.2 RNN的典型应用场景（按输入输出结构分类）

结构类型	输入长度 vs 输出长度	典型任务
N → N	等长	序列标注（如POS tagging）
N → 1	多对一	文本分类、情感分析
1 → N	一对多	图像生成描述、音乐生成
N → M	不定长→不定长	机器翻译、摘要生成（Seq2Seq架构）

注：N表示任意长度序列，M也为任意长度（通常M≠N），这是最灵活的结构，常用于编码器-解码器框架。

二、传统RNN详解与PyTorch实现

我们使用 PyTorch 来构建一个简单的RNN模型，逐步演示不同情况下的输入输出行为。

python 复制代码

import torch
import torch.nn as nn

# 定义RNN模型
rnn = nn.RNN(input_size=5, hidden_size=6, num_layers=1)

# 构造输入：(sequence_len, batch_size, input_dim)
input_data = torch.randn(3, 2, 5)  # 3个时间步，2个样本，每样本5维特征
h0 = torch.zeros(1, 2, 6)          # 初始隐状态 (num_layers, batch_size, hidden_size)

output, hn = rnn(input_data, h0)

print("Output shape:", output.shape)  # [3, 2, 6] -> 每个时间步都有输出
print("Final hidden state shape:", hn.shape)  # [1, 2, 6]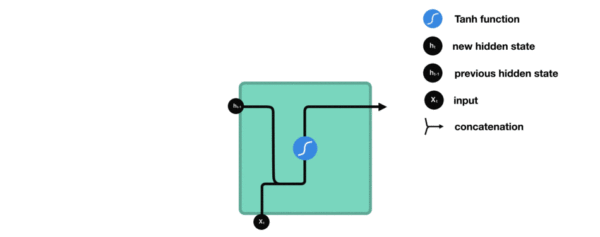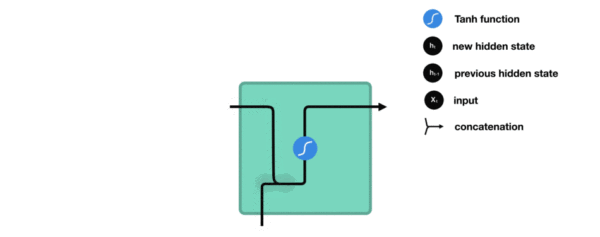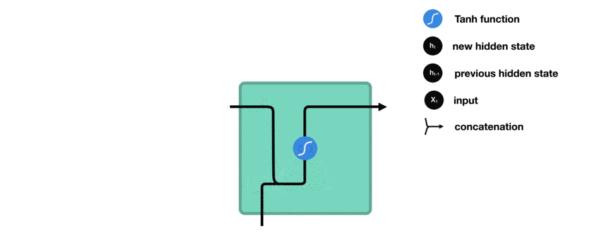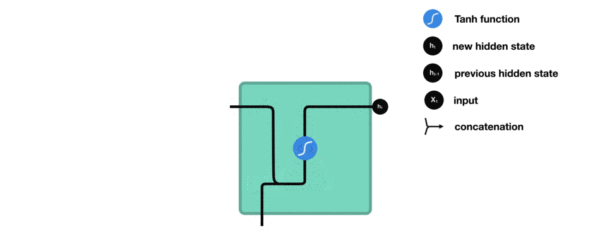

关键点解析：

output[-1] 与 hn 是否相等？
- 是的！对于单层RNN，最后一个时间步的输出 output[-1] 就等于最终隐藏状态 hn。
h0 可省略吗？
- 可以。如果不提供 h0，PyTorch 默认初始化为全零张量。
batch_first 参数的作用
python 复制代码
```
rnn = nn.RNN(..., batch_first=True)  # 输入形状变为 (batch, seq_len, feature)
```
- 默认为 False，输入格式为 (seq_len, batch, features)
- 设置为 True 后更符合直觉，便于调试和可视化。
逐样本送入 vs 一次性送入结果一致
- 虽然教学时常拆开看每一步计算，但实际训练中都是批量处理，两者等价。

三、LSTM：长短时记忆网络 ------ 解决长序列难题

尽管RNN理论上能记住长期信息，但在实践中由于梯度消失/爆炸 问题，很难学习超过几十步的依赖。

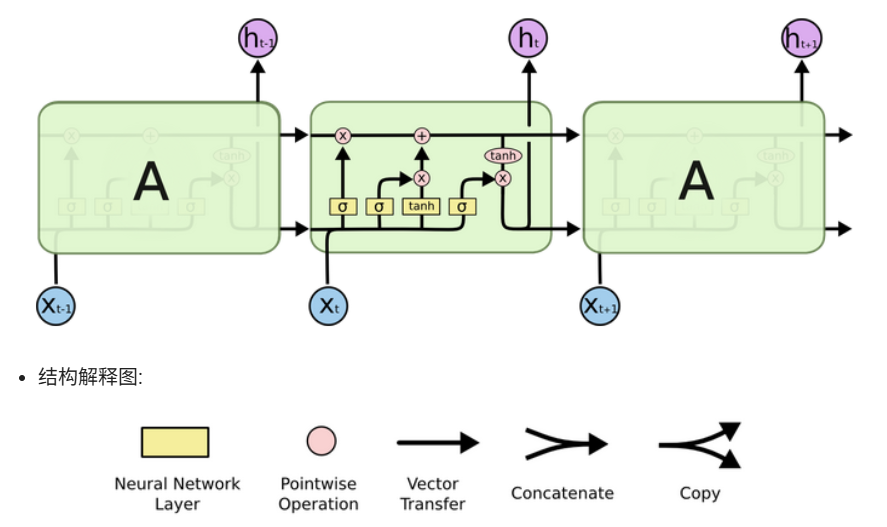
3.1 LSTM核心思想

LSTM（Long Short-Term Memory） 由Hochreiter & Schmidhuber于1997年提出，引入了细胞状态（Cell State） 和三个门控机制来控制信息流动：

遗忘门（Forget Gate）：决定丢弃哪些旧信息
输入门（Input Gate）：决定新增哪些新信息
输出门（Output Gate）：决定输出哪些信息

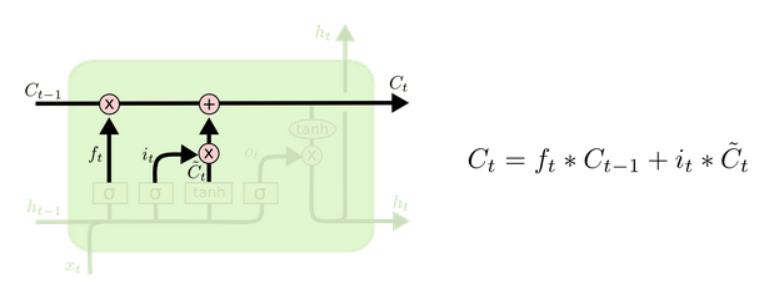
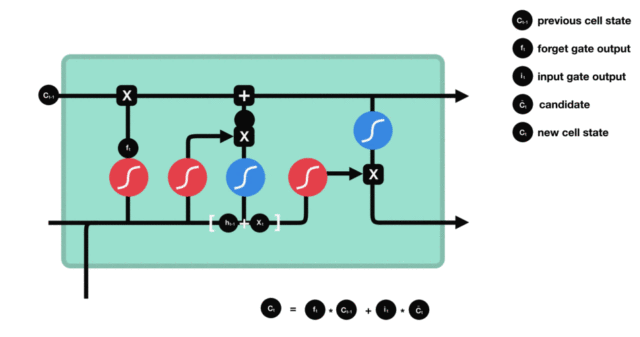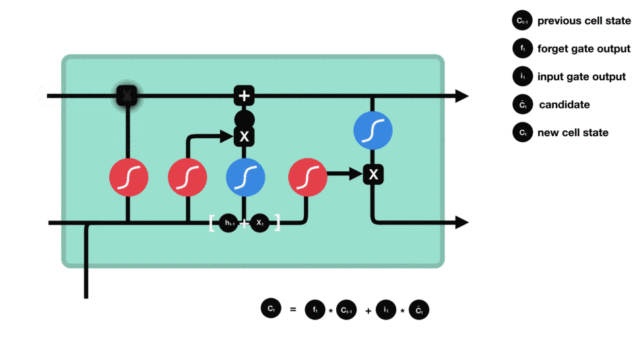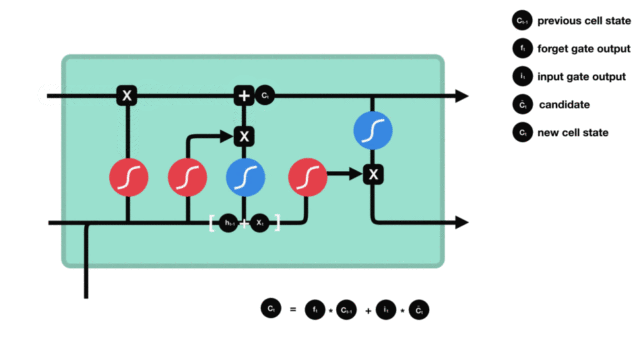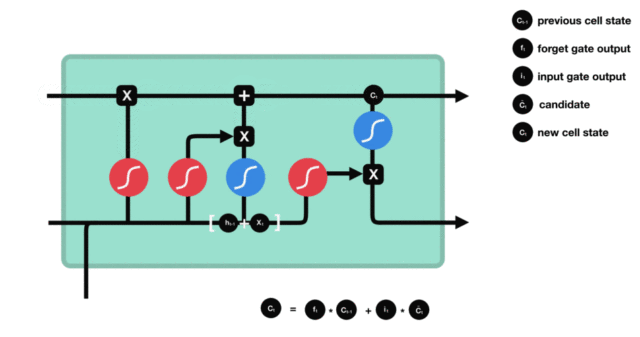
3.2 LSTM内部结构详解

设当前输入为 xtx_txt，上一时刻隐藏状态为 ht−1h_{t-1}ht−1

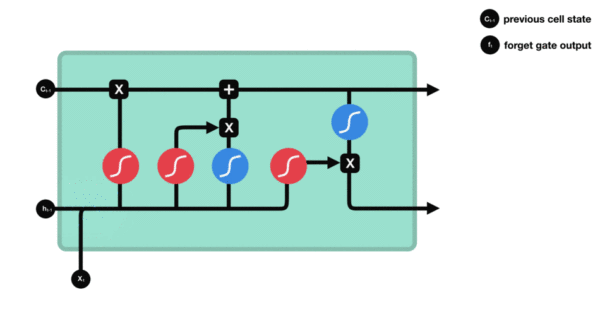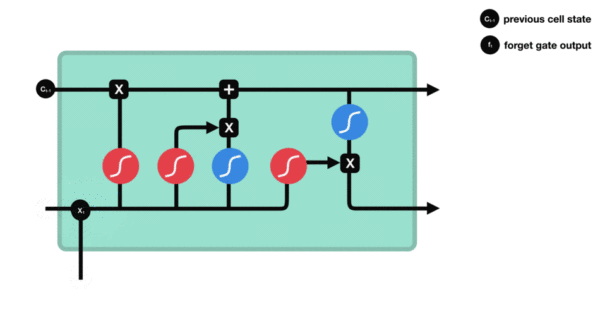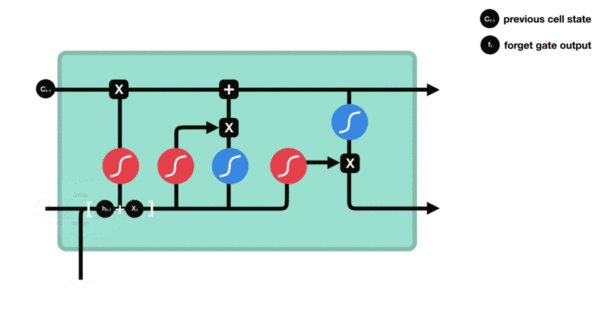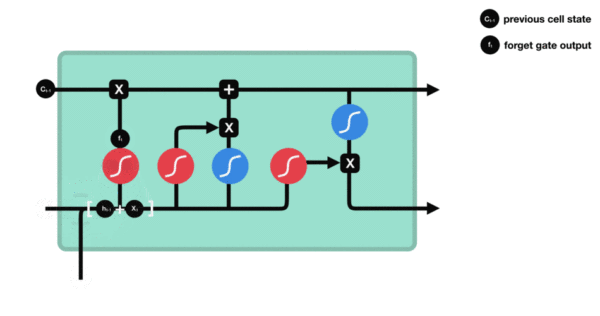
（1）遗忘门

ft=σ(Wf⋅[ht−1,xt]+bf) f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) ft=σ(Wf⋅[ht−1,xt]+bf)

→ 控制保留多少上一时刻的细胞状态 Ct−1C_{t-1}Ct−1

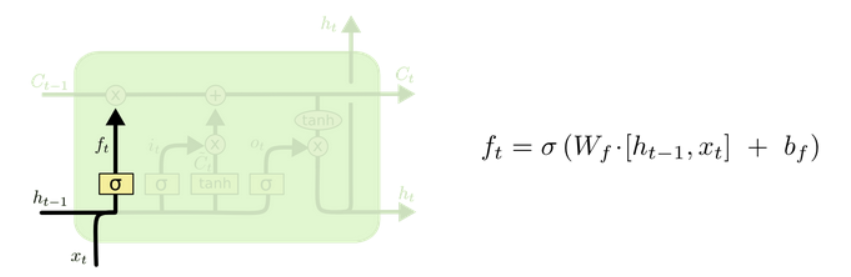
（2）输入门

it=σ(Wi⋅[ht−1,xt]+bi)C~t=tanh⁡(WC⋅[ht−1,xt]+bC) i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ \tilde{C}t = \tanh(W_C \cdot [h{t-1}, x_t] + b_C) it=σ(Wi⋅[ht−1,xt]+bi)C~t=tanh(WC⋅[ht−1,xt]+bC)

→ 决定候选值 C~t\tilde{C}_tC~t 中有多少被写入细胞状态

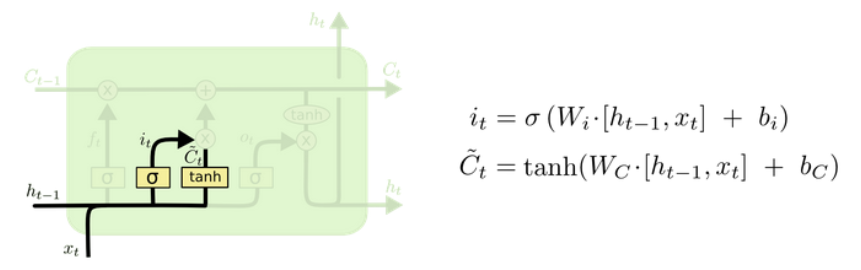
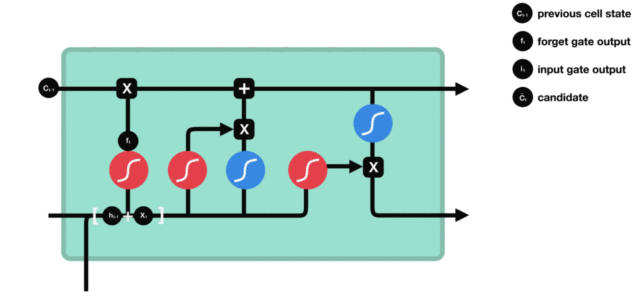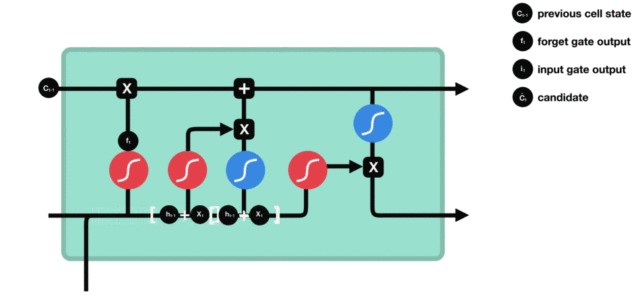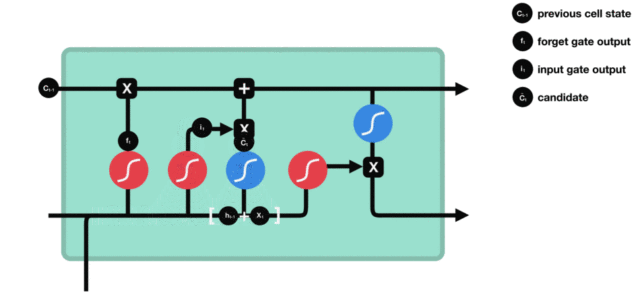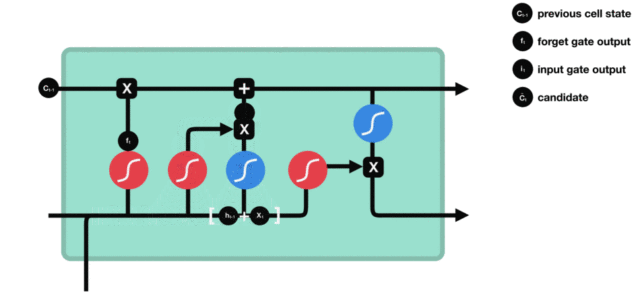
（3）细胞状态更新

Ct=ft⊙Ct−1+it⊙C~t C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t Ct=ft⊙Ct−1+it⊙C~t

这里的加法操作是关键！避免了纯连乘导致的梯度衰减，显著缓解梯度消失。

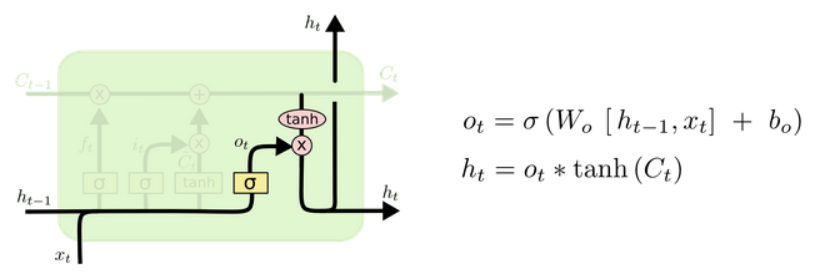
（4）输出门

ot=σ(Wo⋅[ht−1,xt]+bo)ht=ot⊙tanh⁡(Ct) o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ h_t = o_t \odot \tanh(C_t) ot=σ(Wo⋅[ht−1,xt]+bo)ht=ot⊙tanh(Ct)

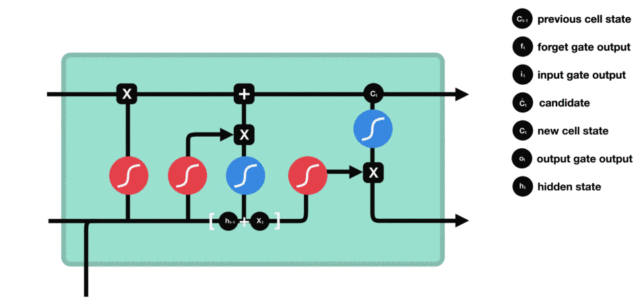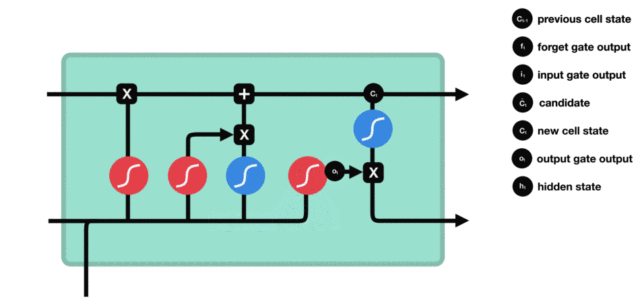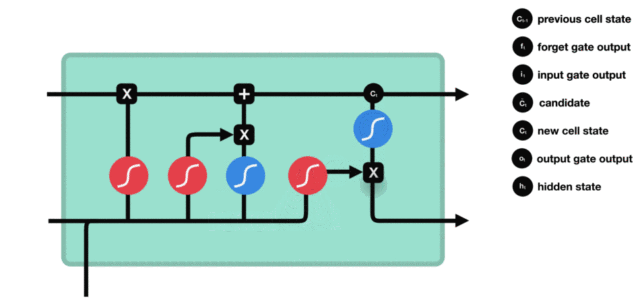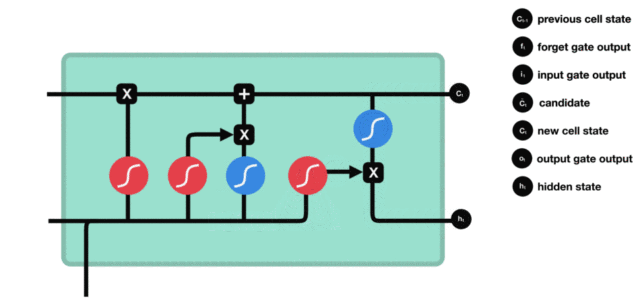
3.3 PyTorch实现LSTM

python 复制代码

lstm = nn.LSTM(input_size=5, hidden_size=6, num_layers=1)

input_data = torch.randn(3, 2, 5)
h0 = torch.zeros(1, 2, 6)
c0 = torch.zeros(1, 2, 6)

output, (hn, cn) = lstm(input_data, (h0, c0))

print("Output shape:", output.shape)     # [3, 2, 6]
print("Hidden shape:", hn.shape)         # [1, 2, 6]
print("Cell state shape:", cn.shape)     # [1, 2, 6]

注意：LSTM有两个隐藏状态输出：hn（隐状态）和 cn（细胞状态）

3.4 为什么LSTM能缓解梯度消失？

细胞状态采用"加法"更新：
- 不同于RNN的纯非线性变换，LSTM的 CtC_tCt 更新包含直接的加法路径，允许梯度"无损"地向前传播较长时间。
门控机制选择性记忆：
- 遗忘门可以选择性地清空无关历史信息，减少无效梯度累积；
- 输入门只保留重要新信息，降低噪声干扰。
tanh与sigmoid组合稳定训练过程

虽然不能完全杜绝梯度问题，但在大多数任务中表现远超传统RNN。

四、GRU：更简洁高效的门控单元

GRU（Gated Recurrent Unit） 是Cho等人在2014年提出的LSTM简化版，仅用两个门就实现了类似性能，且参数更少、训练更快。

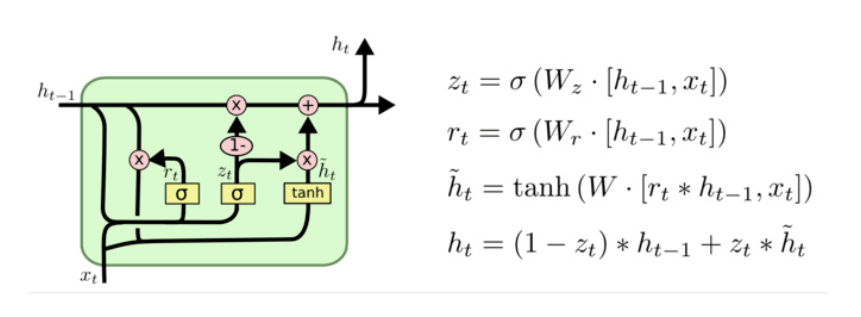
4.1 GRU核心结构

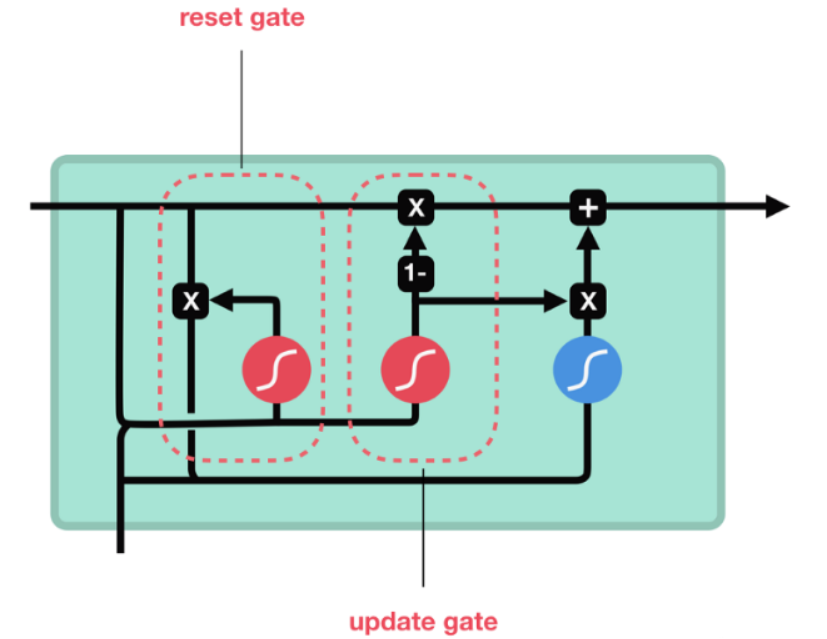
（1）重置门（Reset Gate）

rt=σ(Wr⋅[ht−1,xt]) r_t = \sigma(W_r \cdot [h_{t-1}, x_t]) rt=σ(Wr⋅[ht−1,xt])

→ 控制上一时刻隐藏状态 ht−1h_{t-1}ht−1 对当前候选状态的影响程度

（2）更新门（Update Gate）

zt=σ(Wz⋅[ht−1,xt]) z_t = \sigma(W_z \cdot [h_{t-1}, x_t]) zt=σ(Wz⋅[ht−1,xt])

→ 决定新旧状态的混合比例

（3）候选隐藏状态

h~t=tanh⁡(W⋅[rt⊙ht−1,xt]) \tilde{h}t = \tanh(W \cdot [r_t \odot h{t-1}, x_t]) h~t=tanh(W⋅[rt⊙ht−1,xt])

（4）最终隐藏状态

ht=zt⊙h~t+(1−zt)⊙ht−1 h_t = z_t \odot \tilde{h}t + (1 - z_t) \odot h{t-1} ht=zt⊙h~t+(1−zt)⊙ht−1

直观理解：

当 zt≈1z_t ≈ 1zt≈1：几乎完全使用新状态 h~t\tilde{h}_th~t

当 zt≈0z_t ≈ 0zt≈0：几乎保持旧状态 ht−1h_{t-1}ht−1

相当于自动调节"记忆强度"

4.2 PyTorch实现GRU

python 复制代码

gru = nn.GRU(input_size=5, hidden_size=6, num_layers=1)
input_data = torch.randn(3, 2, 5)
h0 = torch.zeros(1, 2, 6)

output, hn = gru(input_data, h0)

print("Output shape:", output.shape)  # [3, 2, 6]
print("Final hidden state:", hn.shape) # [1, 2, 6]

GRU只有单一隐藏状态，比LSTM更轻量。

五、双向结构：Bi-LSTM 与 Bi-GRU

很多时候，当前词的意义不仅取决于前面的内容，也受后续上下文影响。例如：

"他打开了银行账户。"

vs

"他走进了银行大楼。"

同一个"银行"，含义不同，需结合前后文判断。

5.1 Bi-LSTM/Bi-GRU 原理

分别运行一次正向LSTM和反向LSTM
将两个方向的输出拼接（concatenate）得到最终表示
增强语义感知能力，尤其适用于命名实体识别（NER）、问答系统等任务

python 复制代码

# 双向LSTM示例
bilstm = nn.LSTM(input_size=5, hidden_size=6, num_layers=1, bidirectional=True)
output, (hn, cn) = bilstm(input_data)

print("Bi-LSTM Output shape:", output.shape) 
# [3, 2, 12] -> 6*2 (正向+反向)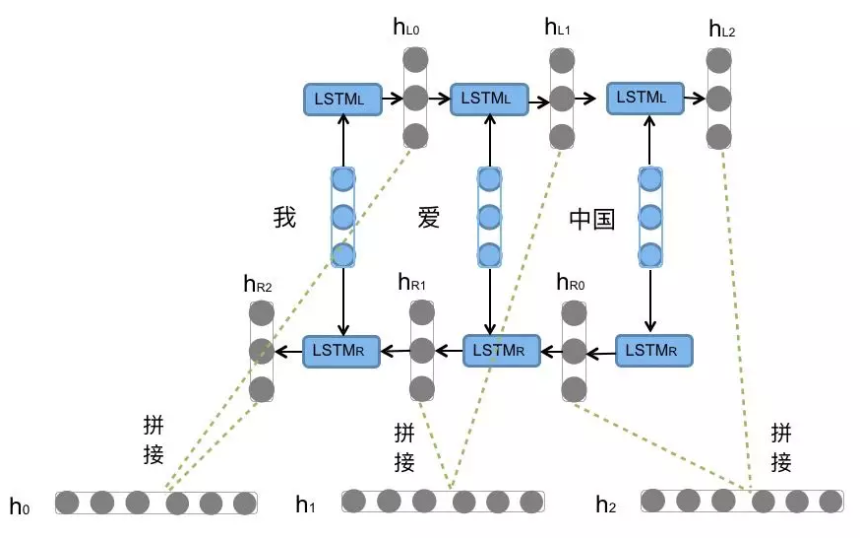

缺点：参数翻倍，计算成本上升；不适合实时流式推理（需要看到完整序列）

六、模型对比总结

模型	是否有门控	参数量	训练速度	长序列建模能力	是否支持并行
RNN	X	少	快	差	X
LSTM	√（3门）	多	慢	好	X
GRU	√（2门）	中	较快	好	X
Bi-LSTM	√	更多	慢	很好	X
Bi-GRU	√	较多	较慢	好	X

选型建议：

简单短文本分类 → RNN 或 GRU

长文本、高精度需求 → LSTM / Bi-LSTM

资源有限、追求效率 → GRU

上下文敏感任务（如NER）→ Bi-GRU / Bi-LSTM

实时应用 → 单向模型优先

七、RNN系列模型的局限性与未来演进

虽然LSTM和GRU极大提升了RNN的能力，但仍存在根本缺陷：

无法并行计算 ：必须按时间步依次执行，训练效率低
长距离依赖仍有瓶颈 ：即使有门控，过长序列仍可能遗忘早期信息
位置信息缺失：没有显式的位置编码机制

正是这些限制催生了 Transformer 架构 的诞生（2017年，《Attention Is All You Need》），通过自注意力机制（Self-Attention） 实现全局依赖建模与高度并行化，成为当前大模型（如BERT、GPT系列）的基础。

所以说：RNN是序列建模的奠基者，Transformer是新时代的引领者。

总结：RNN家族知识图谱

模型	核心创新	优势	局限性
RNN	循环结构，共享参数	结构简单，资源消耗小	梯度消失，难学长依赖
LSTM	三门+细胞状态	显著缓解梯度问题，适合长序列	结构复杂，训练慢
GRU	两门合并，简化LSTM	性能接近LSTM，参数更少，训练更快	仍无法并行
Bi-RNN	双向扫描，融合前后文信息	提升上下文理解能力	推理延迟高，不适用于流式任务

写在最后

RNN虽已不再是SOTA（State-of-the-Art），但它所体现的"记忆"与"递归"思想深刻影响了整个深度学习的发展。掌握RNN及其变体，不仅是理解现代NLP模型演变的关键一步，也是打好序列建模基础的必经之路。