从零复现论文（1）——通感一体化实现协作基站分配与资源分配（CBARA）策略

1.主题

文章是2025年最新的9月发表在axriv上的文章，解决多基站场景下多目标感知与通信的联合优化问题，核心是平衡有限资源（功率、带宽）在感知精度与通信速率间的分配

2.创新点

联合优化 "基站分配（哪个基站服务哪个目标 / 用户）""功率分配""带宽分配"；
以 "后验克拉美罗界（PCRLB，感知精度指标）" 和 "可达速率（通信性能指标）" 为优化目标；
在资源约束（总功率、总带宽、基站服务数量）下，通过权重因子平衡感知与通信偏好。

3.文章内容

通感一体化的惯用手段就是在考虑一种特定的场景下对通信资源和感知资源进行折中、平衡的方式，通常将问题建模为一个多约束的优化问题，根据这种特定环境下对于通信和感知性能的影响构建方程，然后结合"交替优化"等方法来求解最优的目标函数，并确定资源的配置策略。在通信系统领域，发射带宽和功率直接影响系统的性能指标，例如可实现速率、误码率等[9]-[12]。同理，在雷达技术中，感知精度的评估标准------包括克拉美-罗下界（CRLB）和后验克拉美-罗下界PCRLB）------同样与系统功率及可用带宽密切相关。

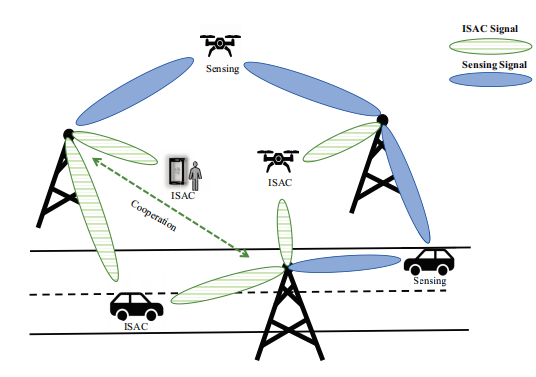
3.1系统模型

基站有K个，目标有Q个，ISAC用户有I个，总共的目标是M=Q+I个，分时隙有n个。

第n个时隙内的第m个目标的状态是这样：

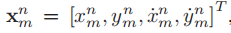
两对x,y是位置和速度。

第n个时隙内第k个基站的发射信号：

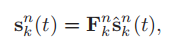
F是波束成形向量，M'是第k个基站能服务的目标数量。此处k~[1,M']。F的公式是这样：

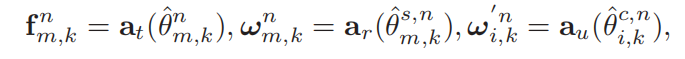
每个BS都采用间距等于半波长的均匀线性阵列（ULA），接收和发射的转向矢量（steering vector）:

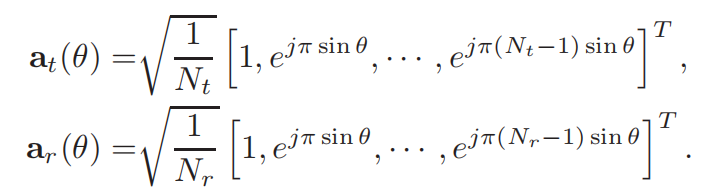
（1）感知信号模型

第n个时隙的第k个基站接收的回波：（感觉就是感知信号，因为接收回波，是雷达才有这种功能）

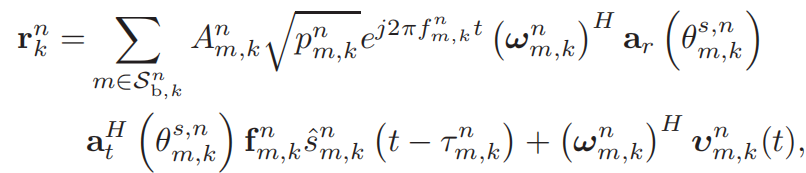
（2）通信信号模型

类似的，ISAC接收的通信信号：

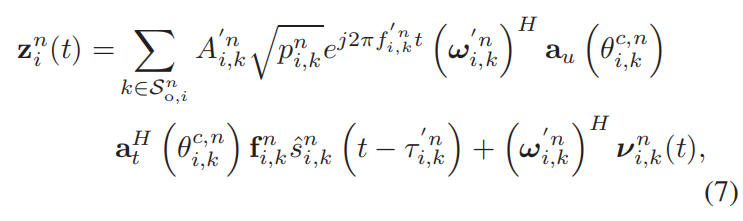
w和F一样都是波束成形矢量，由AOD，和AOA组成

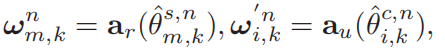
（3）通信性能评估（可达速率 achievable rate）

第n个时隙中，第k个BS与第i个ISAC用户通信的接收信噪比，由下式给出：

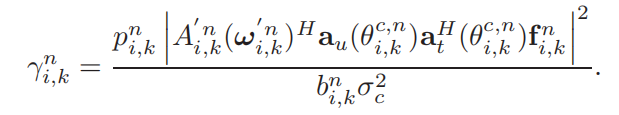
通信信道增益（不懂为什么长这样）

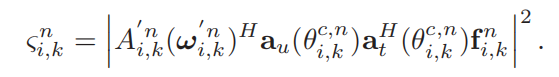
第i个用户的可达速率（不懂为什么长这样）

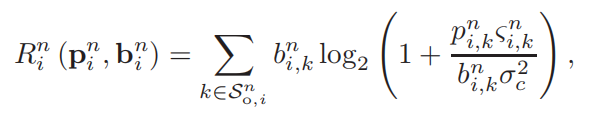
b是第k个BS分配给第i个用户的带宽。关键来了 ：P 和b 分别是第i个用户的功率和带宽分配向量**，也是后续作为优化目标函数需要求解的变量。**

（4）感知性能评估（PCRLB）

描述状态转移的矩阵：

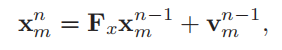
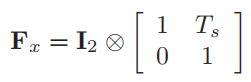
注意，F作为状态转移矩阵，应该是如下表示，因为x是位置，x'是速度，要和T时间相乘：

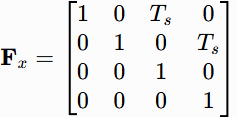
所以有

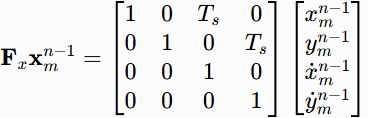
加入过程噪声后，完整状态转移方程为：

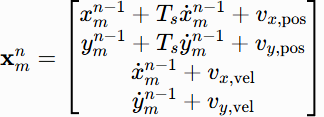
**因此，**在第n个时隙，对第m个对象的第k个BS的测量表示为：

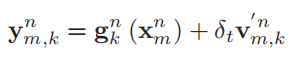
这里发现有的公式后面是逗号，有的是句号，公式间是有关联的！

g(·)是代表一种非线性运算

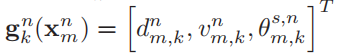
其中：

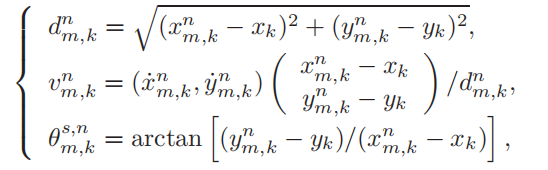
3个变量代表第m个物体相对于第k个BS的距离、速度和方位角（不懂为什么只有一个角度，可能是做的二维），这些关于测量的变量，引入误差自不必说。

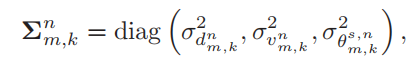
距离，速度，角度的克拉美罗界：

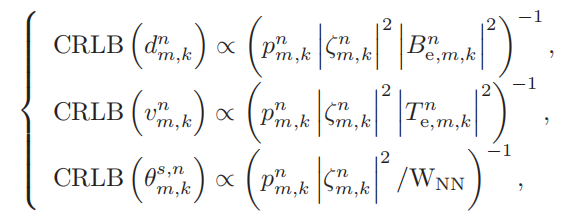
B,T,W文中有引用和解释说明，分别表示有效带宽、有效持续时间、接收天线的零到零波束宽度，看不懂，不管。

注意到感测精度取决于有效带宽B，但通信性能与信号带宽B相关。

本文提出，假设信号是个方波矩形脉冲，可以将上述CRLB变成便携形式

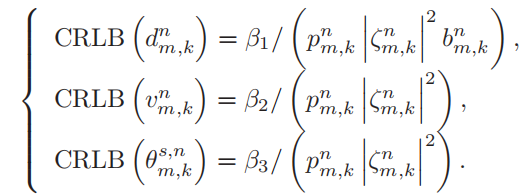
然后又觉得CRLB只表示出了静态的，不如PCRLB结合了测量数据和动态模型

推导了很多公式，没看懂，最后是这样的：

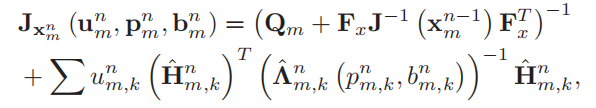
第m个对象的PCRLB为：

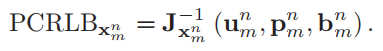
3.2解决问题

从数学角度分析，基站分配与资源管理问题可被定义为一个优化问题，其约束条件基于系统资源。

由于我们的目标是联合优化C&S的性能，因此目标函数可以描述为以下加权ISAC指标：

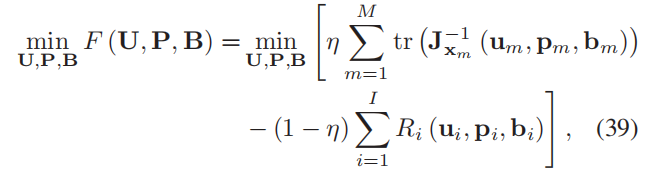
由于共享功率和带宽资源的竞争，PCRLB与可达速率之间存在权衡关系。通过引入系统资源约束条件，CBARA的优化问题可表述为

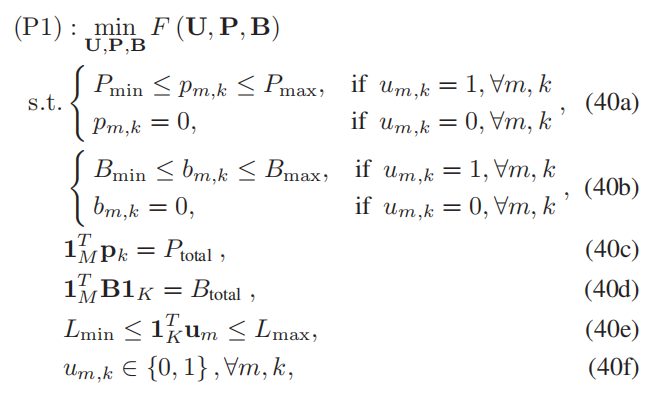
不等式（40a）和（40b）表明，基站为每个对象分配的功率与带宽资源均受特定限制。最小值确保各对象获得足够的通信或感知性能，而最大值则防止资源过度分配并维持系统效率。约束条件（40c）和（40d）分别代表基站的发射功率约束及整个系统的总带宽约束。最后，不等式（40e）规定了同一对象可由多少个基站同时服务，这是基于有限资源预算的考量。

为了求雅可比矩阵的逆方便，用半正定松弛条件等效。

解法

由于式（43g）中的二元约束以及功率与带宽变量的耦合特性，上述问题具有非凸性特征，直接求解难以获得全局最优解。将其分解为基站分配和资源分配两个步骤，从而获得次优解。首先采用启发式算法设计合理的基站分配方案，规避由二元变量U带来的非凸性问题。随后在给定U值的情况下，式（43）中的约束条件变为线性形式，此时每个b和p的目标函数均呈现凸性。

采用交替优化（AO）方法对功率与带宽变量进行解耦处理，具体步骤如下：

3.3实验方法

假设了3个运动模型

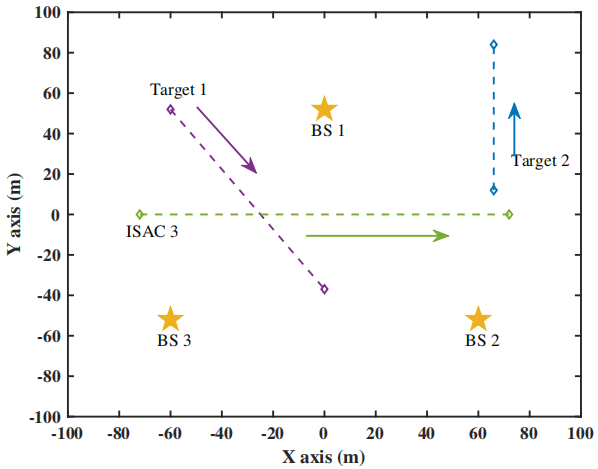
为实验方便，本文将问题进一步简化，代码工程如下：

main.m代码的初始设定：

Matlab 复制代码

%% 1. 参数初始化（根据实际场景调整）
% 系统基本参数
K = 3;          % 基站数量
M = 5;          % 总目标/用户数量（含感知目标和通信用户）
I = 2;          % 纯通信用户数量（M-I为纯感知目标数量）
n = 1;          % 当前时刻
P_total = 10;   % 单基站总功率上限（W）
eta = 0.5;      % 感知-通信权重因子（0偏通信，1偏感知）
syn_error = 1.05;% 同步误差系数
c = 3e8;        % 光速（m/s）
fc = 28e9;      % 载波频率（Hz）
lambda = c / fc;% 信号波长（m）
kappa = 2;      % 路径损耗因子
noise_pwr = -114;% 噪声功率（dBm，后续转为W）
noise_pwr = 10^(noise_pwr/10) / 1000; % 转换为W

% 天线参数
Nt = 8;         % 发射天线数量
Nr = 8;         % 接收天线数量
beam_gafc = 10; % 波束增益（dB）

% 目标/用户位置（3D坐标：x,y,z，单位：m）
position_qn = rand(M, 3, n) * 1000;  % 感知目标位置（0~1000m随机）
position_cn = rand(I, 3, n) * 1000;  % 通信用户位置
base = rand(K, 3) * 500;             % 基站位置（0~500m随机）

% 其他参数
Rcs = 10;               % 目标雷达截面积（m²）
Q_m = repmat(0.1*eye(4), [1,1,M]);  % 运动噪声方差矩阵（4x4xM）
F_x = [1 0 0.1 0;       % 运动转移矩阵（假设采样时间0.1s的匀速模型）
    0 1 0 0.1;
    0 0 1 0;
    0 0 0 1];
PCRLB = repmat(10*eye(4), [1,1,M,n]); % 上一时刻PCRBL（初始化）
u = randi([0,1], K, M); % 基站-用户关联矩阵（0/1随机初始化）
b = rand(K, M) * 10;    % 带宽分配（MHz，后续转为Hz）
II = eye(4);            % 4x4单位矩阵

关键的优化求解代码如下，注意需要安装CVX工具箱（文中也有提到）：

Matlab 复制代码

cvx_begin sdp
% 变量声明（无约束，适配所有CVX版本）
    variable p(K,M);  % 功率分配变量
    variable D(4,4,M);  % 辅助矩阵变量（PCRBL的代理变量）
    expression J_m(4,4,M);  % 总费雪矩阵（CVX表达式，用于暂存中间结果）
    expression sum_D;       % PCRBL总和（目标函数项）

% 初始化PCRBL总和
sum_D = 0;

% 遍历所有目标/用户，计算费雪矩阵和PCRBL
for m = 1:M
    % 1. 计算先验费雪矩阵（基于上一时刻PCRBL）
    J_p = inv(Q_m(:,:,m) + F_x * PCRLB(:,:,m,n) * F_x');

    % 2. 计算数据费雪矩阵（多基站观测贡献）
    J_y = zeros(4,4);
    
    for k = 1:K
        if u(k,m) == 1  % 仅计算关联的基站
            % 2.1 计算距离、角度、速度的CRB（调用子函数）
            CRB_d_k = calcu_CRB_d(position_qn(m,:,n), base(k,:), Rcs, lambda, kappa, beam_gafc, Nr, noise_pwr);
            CRB_theta_k = calcu_CRB_theta(position_qn(m,:,n), base(k,:), Rcs, lambda, kappa, beam_gafc, Nr, noise_pwr);
            CRB_v_k = calcu_CRB_v(position_qn(m,:,n), base(k,:), Rcs, lambda, kappa, beam_gafc, Nr, noise_pwr);

            % 2.2 计算观测噪声方差矩阵A_k（3x3，对应距离、角度、速度）
            A_k = diag([b(k,m)*1e6*(syn_error*CRB_d_k)^(-1), ...  % 距离项（带宽转为Hz）
                (syn_error*CRB_theta_k)^(-1), ...          % 角度项
                (syn_error*CRB_v_k)^(-1)]);                % 速度项

            % 2.3 计算雅克比矩阵H_k（4x3：4维状态→3维观测）
            % 构造目标状态向量：[x, y, vx, vy]（4维）
            target_x = position_qn(m,1,n);
            target_y = position_qn(m,2,n);
            vx = 10;  % 假设速度，可根据实际调整
            vy = 10;
            target_state = [target_x, target_y, vx, vy];
            H_k = calcu_Jacobih(target_state, base(k,:));  % 调用子函数

            % 2.4 累加数据费雪矩阵（与功率p正相关）
            J_y = J_y + p(k,m) * H_k * A_k * H_k';
        end
    end

    % 3. 总费雪矩阵 = 先验 + 数据（加入数值正则项确保正定性）
    J_m(:,:,m) = J_p + J_y + 1e-8 * II;

    % 4. 累加PCRBL（通过辅助变量D的迹表示，D=J_m^{-1}）
    sum_D = sum_D + trace(D(:,:,m));
end

% 6. 计算通信可达速率（调用子函数）
Rate = calcu_rate(I, K, squeeze(position_cn(:,:,n)), b(:,M-I+1:end), p(:,M-I+1:end), Nt, Nr, base, fc, kappa, noise_pwr, u(:,M-I+1:end));

% 7. 定义目标函数（最小化：感知误差加权 - 通信速率加权）
objective = eta * sum_D - (1 - eta) * Rate;
minimize(objective);

% 8. 约束条件
subject to
% 8.1 半正定约束（舒尔补引理：确保D=J_m^{-1}）
for m = 1:M
    [D(:,:,m) II; II J_m(:,:,m)] == semidefinite(8);
end

% 8.2 功率约束（单个用户+基站总功率）
for k = 1:K
    sum_p_k = 0;  % 单基站总功率累加
    for m = 1:M
        if u(k,m) == 1
            % 非负功率（去除较强的单用户下限，避免不可行）
            p(k,m) >= 0;
            p(k,m) <= P_total;
            sum_p_k = sum_p_k + p(k,m);
        else
            p(k,m) == 0;  % 未关联用户功率为0
        end
    end
    sum_p_k <= P_total;  % 基站总功率不超限
end
cvx_end

这是楼主的优化结果，一个小实验

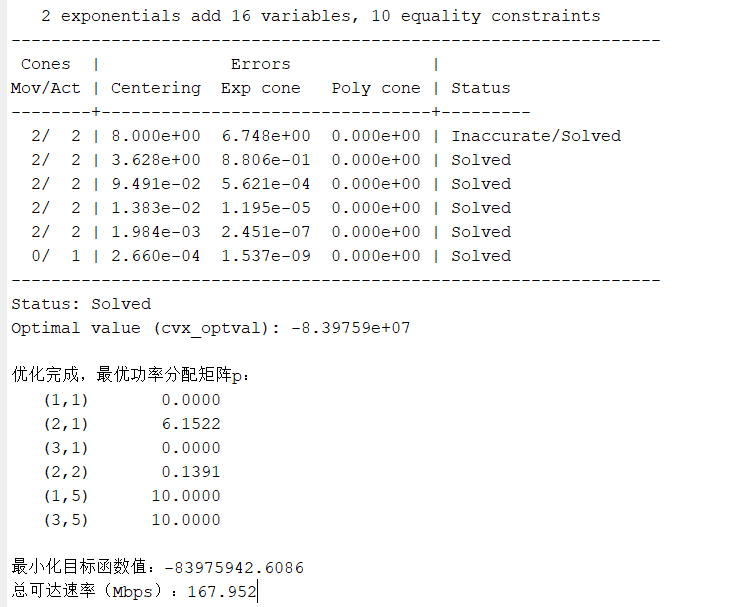
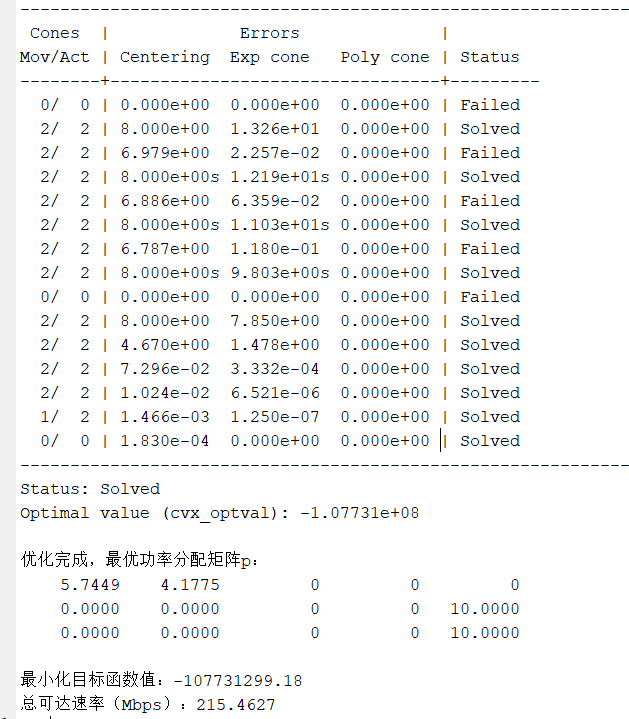
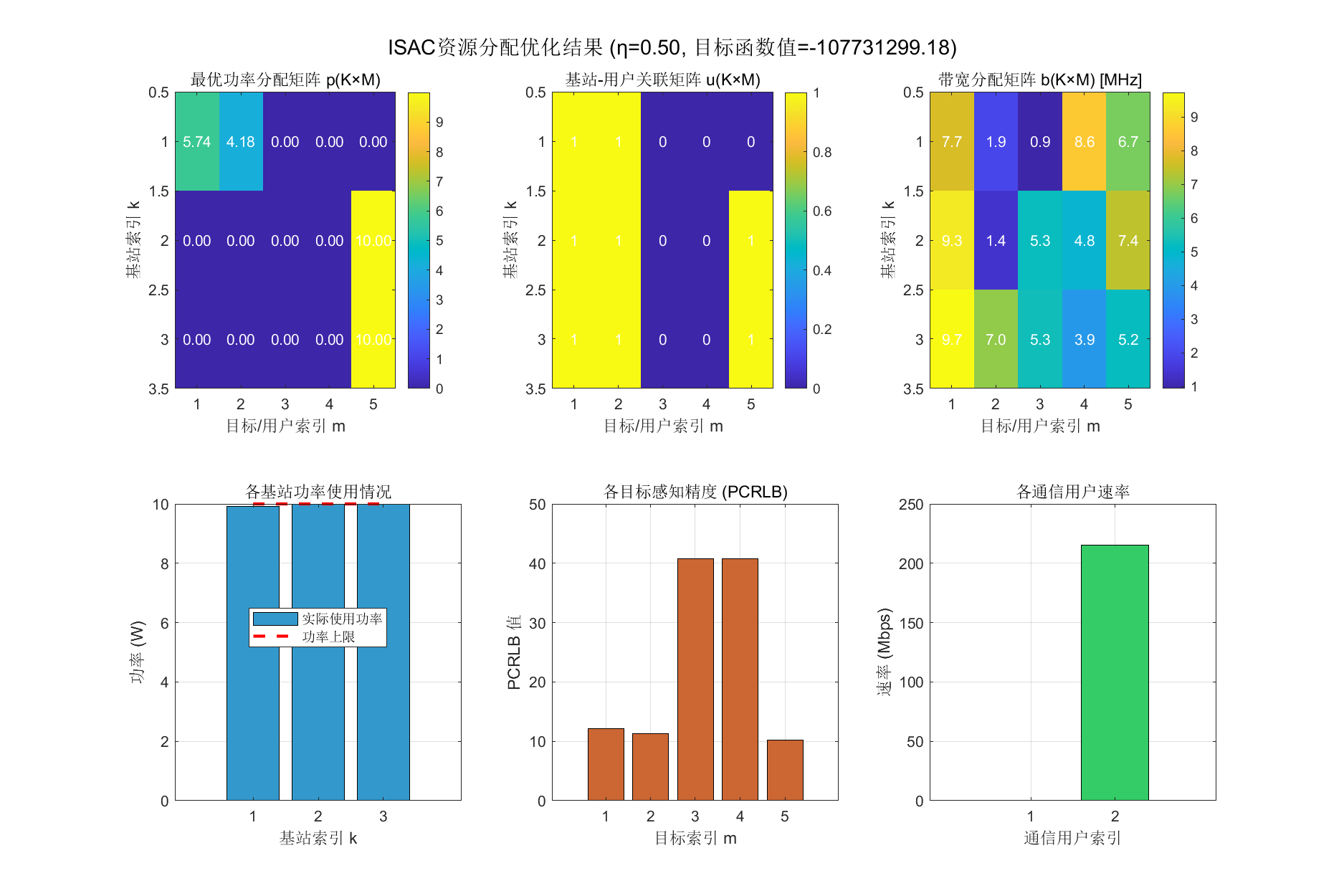
总结

主要学习到问题的架构，从最最基本的公式推导到当前场景所需的问题，在叙述系统模型的时候一定要将特殊化的问题一般化，在仿真的时候，越简单越好，注意行文过程要让读者能跟上逻辑。

处理优化问题，一定要借助数学工具，难以理解的是，这种文章的诞生，其利用的数学方法是天然存在的，还是作者有相应的积累，不敢想是自己探索着找到的方法有多难。