文章目录
- 上文链接
- [1. 选数 ⭐](#1. 选数 ⭐)
-
- [(1) 解题思路](#(1) 解题思路)
- [(2) 代码实现](#(2) 代码实现)
- [2. 飞机降落 ⭐⭐](#2. 飞机降落 ⭐⭐)
-
- [(1) 解题思路](#(1) 解题思路)
- [(2) 代码实现](#(2) 代码实现)
- [3. 八皇后 ⭐⭐](#3. 八皇后 ⭐⭐)
-
- [(1) 解题思路](#(1) 解题思路)
- [(2) 代码实现](#(2) 代码实现)
- [4. 数独 ⭐⭐](#4. 数独 ⭐⭐)
-
- [(1) 解题思路](#(1) 解题思路)
- [(2) 代码实现](#(2) 代码实现)
上文链接
1. 选数 ⭐
【题目链接】
P1036 [NOIP 2002 普及组\] 选数 - 洛谷](https://www.luogu.com.cn/problem/P1036)
【题目描述】
已知 n n n 个整数 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn,以及 1 1 1 个整数 k k k( k < n k<n k<n)。从 n n n 个整数中任选 k k k 个整数相加,可分别得到一系列的和。例如当 n = 4 n=4 n=4, k = 3 k=3 k=3, 4 4 4 个整数分别为 3 , 7 , 12 , 19 3,7,12,19 3,7,12,19 时,可得全部的组合与它们的和为:
3 + 7 + 12 = 22 3+7+12=22 3+7+12=22
3 + 7 + 19 = 29 3+7+19=29 3+7+19=29
7 + 12 + 19 = 38 7+12+19=38 7+12+19=38
3 + 12 + 19 = 34 3+12+19=34 3+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数: 3 + 7 + 19 = 29 3+7+19=29 3+7+19=29。
【输入格式】
第一行两个空格隔开的整数 n , k n,k n,k( 1 ≤ n ≤ 20 1 \le n \le 20 1≤n≤20, k < n k<n k<n)。
第二行 n n n 个整数,分别为 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn( 1 ≤ x i ≤ 5 × 1 0 6 1 \le x_i \le 5\times 10^6 1≤xi≤5×106)。
【输出格式】
输出一个整数,表示种类数。
【示例一】
输入
4 3 3 7 12 19输出
1
【说明/提示】
NOIP 2002 普及组第二题
(1) 解题思路
这其实就是一个组合问题,组合枚举的决策树如下(以从 [1, 2, 3, 4] 中选 3 个数为例):
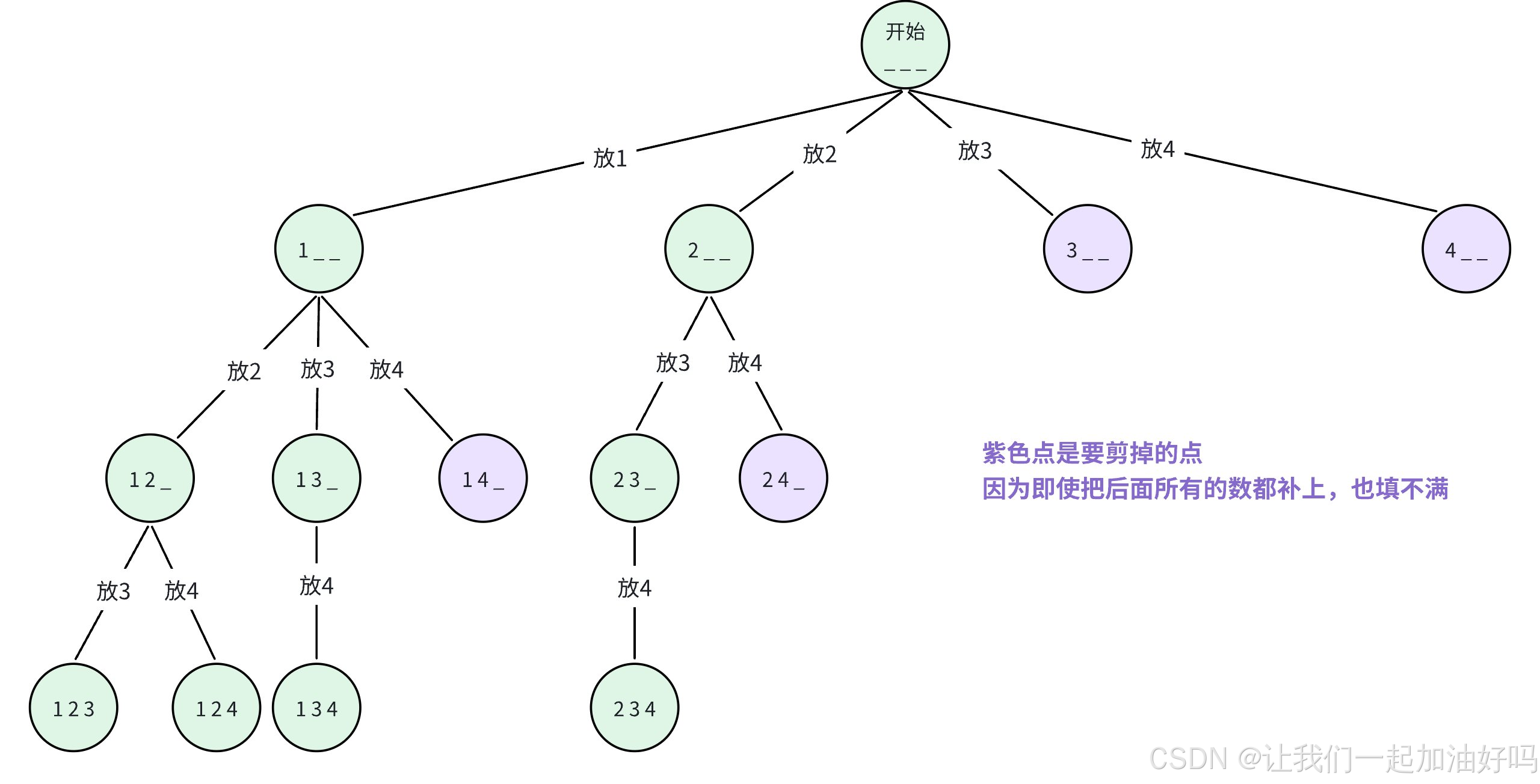
那么这道题中我们只需要在给定的 n 个数中选择 k 个数即可,每枚举出一组,就判断它们的和是否为质数。
(2) 代码实现
cpp
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
const int N = 25;
vector<int> path;
int a[N];
int n, k, ans;
// 判断质数
bool isPrime(int x)
{
if(x <= 1) return false;
for(int i = 2; i <= sqrt(x); i++)
{
if(x % i == 0) return false;
}
return true;
}
// 从 begin 位置开始往后枚举
void dfs(int begin)
{
if(path.size() == k) // 已经选了 k 个数了
{
int t = 0;
for(auto e : path) t += e; // 求和
if(isPrime(t)) ans++;
return;
}
for(int i = begin; i <= n; i++)
{
path.push_back(a[i]);
dfs(i + 1); // 递归到决策树下一层
path.pop_back(); // 回溯,恢复现场
}
}
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> a[i];
dfs(1);
cout << ans;
return 0;
}2. 飞机降落 ⭐⭐
【题目链接】
P9241 [蓝桥杯 2023 省 B\] 飞机降落 - 洛谷](https://www.luogu.com.cn/problem/P9241)
【题目描述】
N N N 架飞机准备降落到某个只有一条跑道的机场。其中第 i i i 架飞机在 T i T_{i} Ti 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 D i D_{i} Di 个单位时间,即它最早可以于 T i T_{i} Ti 时刻开始降落,最晩可以于 T i + D i T_{i}+D_{i} Ti+Di 时刻开始降落。降落过程需要 L i L_{i} Li 个单位时间。
一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不能在前一架飞机完成降落前开始降落。
请你判断 N N N 架飞机是否可以全部安全降落。
【输入格式】
输入包含多组数据。
第一行包含一个整数 T T T,代表测试数据的组数。
对于每组数据,第一行包含一个整数 N N N。
以下 N N N 行,每行包含三个整数 T i , D i , L i T_{i},D_{i},L_{i} Ti,Di,Li。
【输出格式】
对于每组数据,输出
YES或者NO,代表是否可以全部安全降落。
【示例一】
输入
2 3 0 100 10 10 10 10 0 2 20 3 0 10 20 10 10 20 20 10 20输出
YES NO
【说明/提示】
对于第一组数据,可以安排第 3 架飞机于 0 时刻开始降落,20 时刻完成降落。安排第 2 架飞机于 20 时刻开始降落,30 时刻完成降落。安排第 1 架飞机于 30 时刻开始降落,40 时刻完成降落。
对于第二组数据,无论如何安排,都会有飞机不能及时降落。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, N ≤ 2 N \leq 2 N≤2。
对于 100 % 100 \% 100% 的数据, 1 ≤ T ≤ 10 1 \leq T \leq 10 1≤T≤10, 1 ≤ N ≤ 10 1 \leq N \leq 10 1≤N≤10, 0 ≤ T i , D i , L i ≤ 1 0 5 0 \leq T_{i},D_{i},L_{i} \leq 10^{5} 0≤Ti,Di,Li≤105。
蓝桥杯 2023 省赛 B 组 D 题。
(1) 解题思路
看到这题其实会有一个贪心的想法,有点像贪心的区间问题,但是这道题找不到一个固定的贪心策略使用与所有情况。仔细观察数据范围可以发现,飞机的数量最多仅仅只有 10 个,因此这道题明摆着就是让我们枚举,也就是爆搜。
对于给定的所有飞机,我们只需要枚举出它们能组成的所有顺序,也就是全排列 。然后对于每种顺序,判断它们能否安全降落即可,如果有一种可以安全降落,结果就是 YES,否则为 NO。
(2) 代码实现
cpp
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int N = 15;
int T, n;
vector<int> path;
bool vis[N];
bool flag; // 能否安全降落
struct node
{
int t, d, l;
} ap[N];
// 检查对于一种飞机顺序,能否安全降落
bool check()
{
int current_time = 0; // 当前时间
for(int i = 0; i < path.size(); i++) // 索引从 0 开始,按顺序枚举飞机
{
int id = path[i]; // 获取飞机编号
// 有可能上一架飞机降落完毕了下一架飞机都还没来,因此要去较大者
int start_time = max(current_time, ap[id].t); // 实际开始时间
// 检查开始时间是否在允许范围内
// 如果上一架飞机降落完毕之后的时间大于下一架飞机的最晚降落时间
if(start_time > ap[id].t + ap[id].d) return false;
// 更新时间为当前飞机完成时间
current_time = start_time + ap[id].l;
}
return true;
}
void dfs()
{
if(flag) return; // 找到解后剪枝
if(path.size() == n)
{
if(check()) flag = true; // 如果当前情况能够安全降落
return;
}
for(int i = 1; i <= n; i++)
{
if(vis[i]) continue;
path.push_back(i);
vis[i] = true;
dfs(); // 递归到下一层
path.pop_back(); // 恢复现场
vis[i] = false;
}
}
int main()
{
cin >> T;
while(T--)
{
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> ap[i].t >> ap[i].d >> ap[i].l;
}
flag = false;
path.clear(); // 清空路径
memset(vis, 0, sizeof(vis)); // 重置访问标记
dfs();
if(flag) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}3. 八皇后 ⭐⭐
【题目链接】
P1219 [USACO1.5\] 八皇后 Checker Challenge - 洛谷](https://www.luogu.com.cn/problem/P1219)
【题目描述】
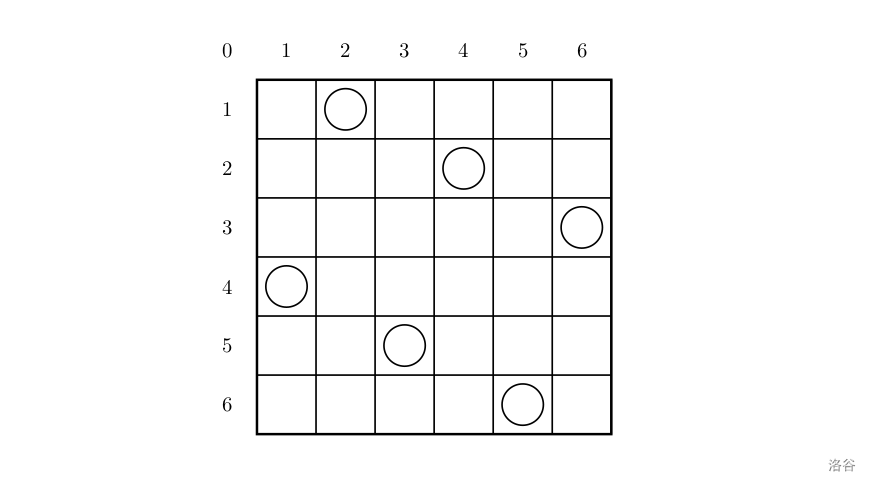
一个如下的 6 × 6 6 \times 6 6×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。
上面的布局可以用序列 2 4 6 1 3 5 2\ 4\ 6\ 1\ 3\ 5 2 4 6 1 3 5 来描述,第 i i i 个数字表示在第 i i i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6 1\ 2\ 3\ 4\ 5\ 6 1 2 3 4 5 6
列号 2 4 6 1 3 5 2\ 4\ 6\ 1\ 3\ 5 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3 3 3 个解。最后一行是解的总个数。
【输入格式】
一行一个正整数 n n n,表示棋盘是 n × n n \times n n×n 大小的。
【输出格式】
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
【示例一】
输入
6输出
2 4 6 1 3 5 3 6 2 5 1 4 4 1 5 2 6 3 4
【说明/提示】
对于 100 % 100\% 100% 的数据, 6 ≤ n ≤ 13 6 \le n \le 13 6≤n≤13。
题目翻译来自NOCOW。
USACO Training Section 1.5
(1) 解题思路
首先画出决策树:
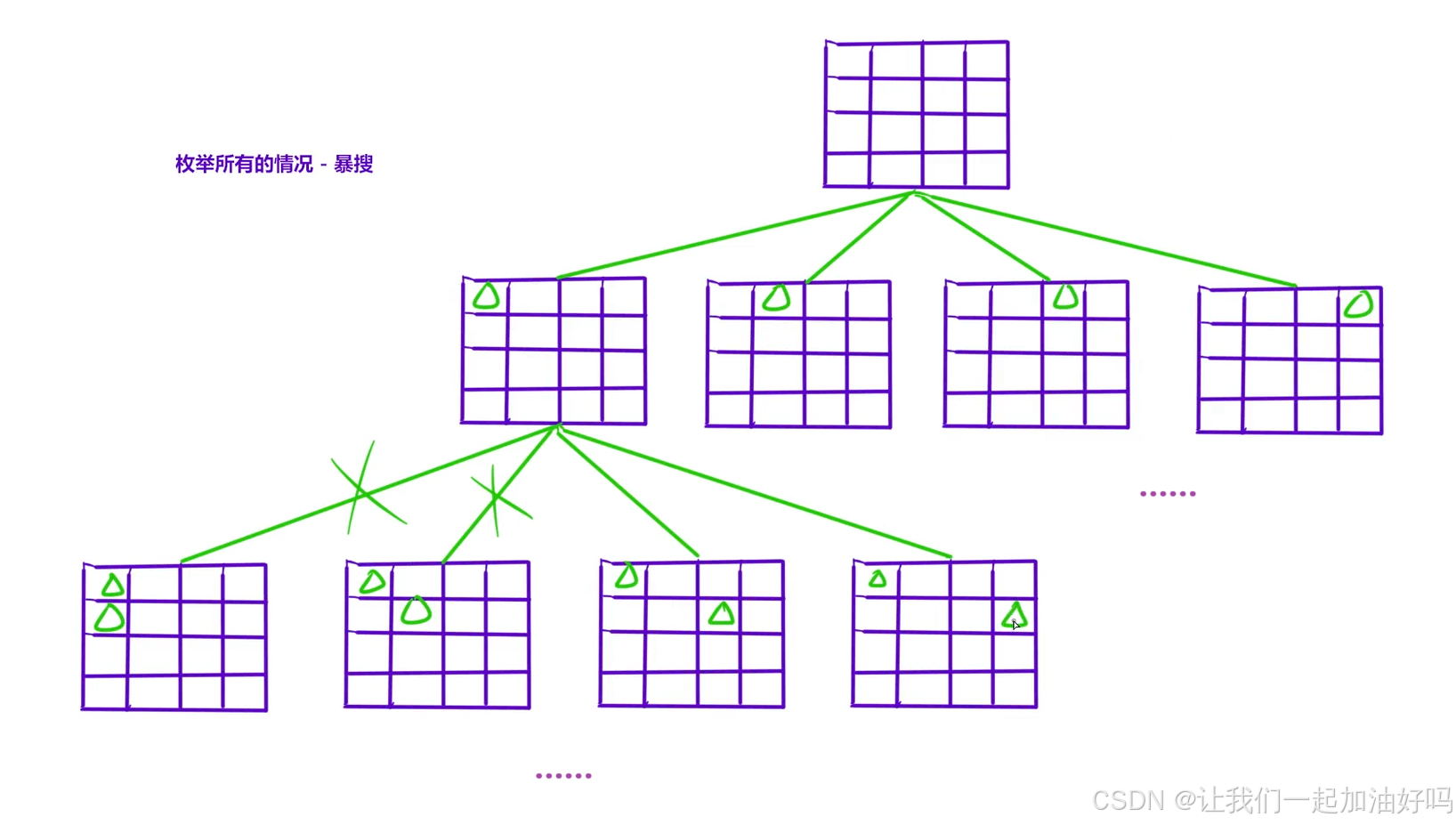
以 "行" 为基准,对于每一行,枚举每一列的摆放位置,对于每一个摆放位置,判断其是否合法,如果合法,就记录摆放位置并继续递归到下一行,否则直接剪枝剪掉。
如何判断是否合法?
对于某一个位置 [r, c](第 r 行第 c 列),我们可以用一个数组 col[i] 来标记第 i 列是否被摆放过棋子。对于斜向,分为两种情况:斜率为正和斜率为负。
对于斜率为正的斜线,根据一次函数 y = x + b y = x + b y=x+b,上面的所有位置一定满足 r − c = b r - c = b r−c=b。其中 b b b 为一固定的常数。所以我们只需要定义一个数组 st1[],其中 st1[i] 表示所有满足 r − c = i r - c = i r−c=i 的位置是否放置了棋子。换句话说,就是如果 [r, c] 上摆放了棋子,那么我们就把 st1[r - c] 置为 true,表示 [r, c] 所在的这条斜线上摆放过棋子了。但是由于 r − c r - c r−c 可能是负数,所以为了不越界,这里统一加上一个 n n n,即将 st1[r - c + n] 置为 true( n n n 为棋盘边长)。
同理,如果两个棋子在同一斜率为负的斜线上时,那么我们定义另外一个数组 st2[],当排放一个棋子时,我们就把 st2[r + c] 置为 true。
(2) 代码实现
cpp
#include<iostream>
#include<vector>
using namespace std;
const int N = 15;
int n;
vector<int> path;
bool col[N], st1[2 * N], st2[2 * N];
int cnt; // 记录情况总数
int k = 3;
void dfs(int r)
{
if(path.size() == n)
{
if(k > 0) // 输出前三种情况
{
for(auto e : path) cout << e << " ";
cout << endl;
k--;
}
cnt++;
return;
}
for(int c = 1; c <= n; c++)
{
// 如果当前纵列和两个斜向上都没有摆放棋子
if(!col[c] && !st1[r - c + n] && !st2[r + c])
{
path.push_back(c);
col[c] = true;
st1[r - c + n] = true;
st2[r + c] = true;
dfs(r + 1); // 递归到下一行去摆放棋子
// 回溯,恢复现场
path.pop_back();
col[c] = false;
st1[r - c + n] = false;
st2[r + c] = false;
}
}
}
int main()
{
cin >> n;
dfs(1); // 从第一行开始枚举
cout << cnt;
return 0;
}4. 数独 ⭐⭐
【题目链接】
【题目描述】
数独是根据 9 × 9 9 \times 9 9×9 盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫内的数字均含 1 − 9 1 - 9 1−9 ,不重复。每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的。
芬兰一位数学家号称设计出全球最难的"数独游戏",并刊登在报纸上,让大家去挑战。
这位数学家说,他相信只有"智慧最顶尖"的人才有可能破解这个"数独之谜"。
据介绍,目前数独游戏的难度的等级有一到五级,一是入门等级,五则比较难。不过这位数学家说,他所设计的数独游戏难度等级是十一,可以说是所以数独游戏中,难度最高的等级。他还表示,他目前还没遇到解不出来的数独游戏,因此他认为"最具挑战性"的数独游戏并没有出现。
【输入格式】
一个未填的数独。
【输出格式】
填好的数独。
【示例一】
输入
8 0 0 0 0 0 0 0 0 0 0 3 6 0 0 0 0 0 0 7 0 0 9 0 2 0 0 0 5 0 0 0 7 0 0 0 0 0 0 0 4 5 7 0 0 0 0 0 1 0 0 0 3 0 0 0 1 0 0 0 0 6 8 0 0 8 5 0 0 0 1 0 0 9 0 0 0 0 4 0 0输出
8 1 2 7 5 3 6 4 9 9 4 3 6 8 2 1 7 5 6 7 5 4 9 1 2 8 3 1 5 4 2 3 7 8 9 6 3 6 9 8 4 5 7 2 1 2 8 7 1 6 9 5 3 4 5 2 1 9 7 4 3 6 8 4 3 8 5 2 6 9 1 7 7 9 6 3 1 8 4 5 2
【说明/提示】
2022-04-17 @farteryhr 贡献了三组 hack 数据。加入了其中两组。第三组过强(来源:https://www.dcc.fc.up.pt/~acm/sudoku.pdf),放在下边供自测。
9 0 0 8 0 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 1 0 0 0 3 0 1 0 0 0 0 0 6 0 0 0 0 4 0 0 0 7 0 7 0 8 6 0 0 0 0 0 0 0 0 0 3 0 1 0 0 4 0 0 0 0 0 2 0 0输出
9 7 2 8 5 3 6 1 4 1 4 6 2 7 9 5 3 8 5 8 3 1 4 6 7 2 9 6 2 4 7 1 8 9 5 3 8 1 7 3 9 5 4 6 2 3 5 9 4 6 2 8 7 1 7 9 8 6 2 1 3 4 5 2 6 5 9 3 4 1 8 7 4 3 1 5 8 7 2 9 6
(1) 解题思路
先画出决策树:
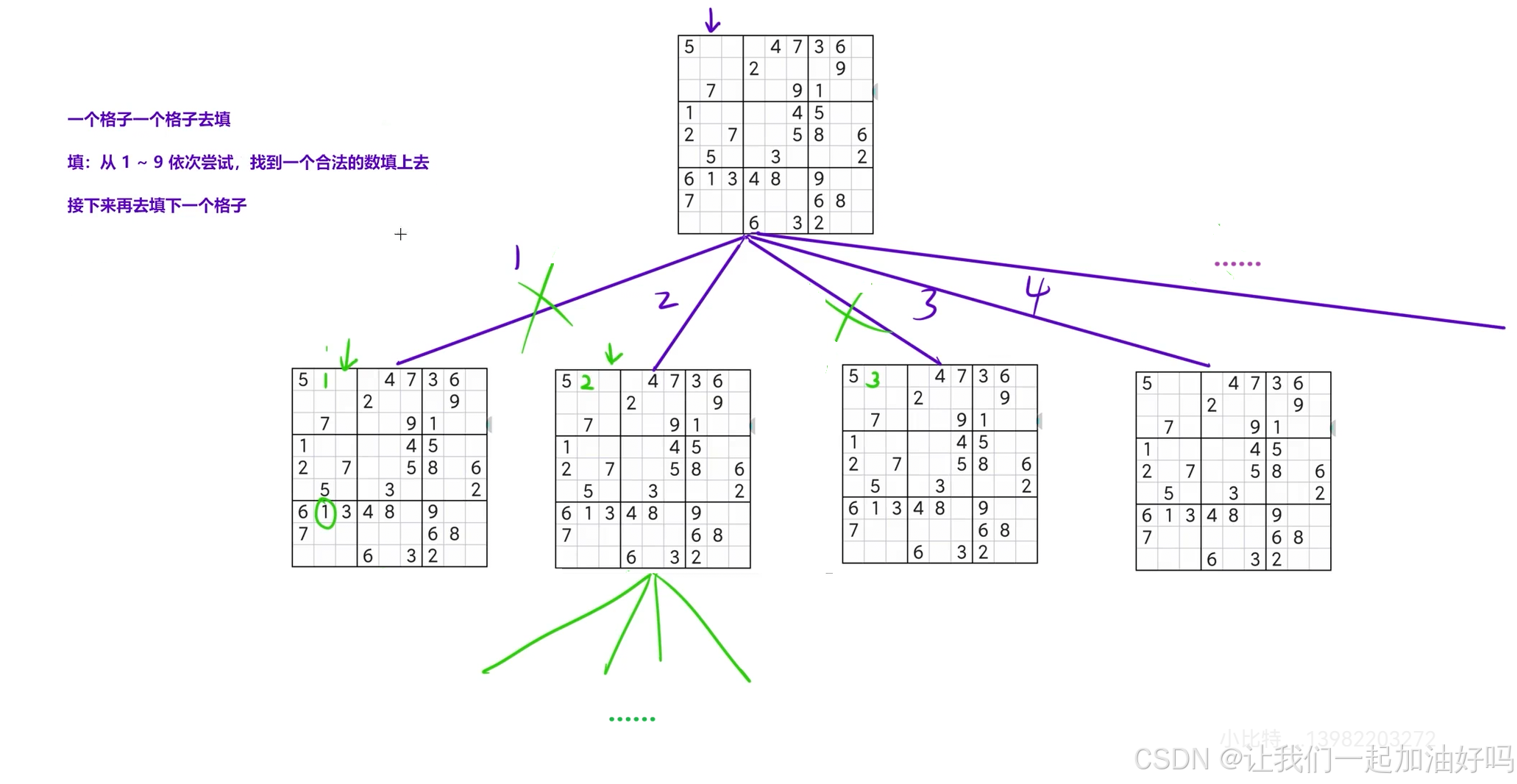
以每一个格子为单位,枚举每一个数,对于每一个数,判断放在该位置是否合法。
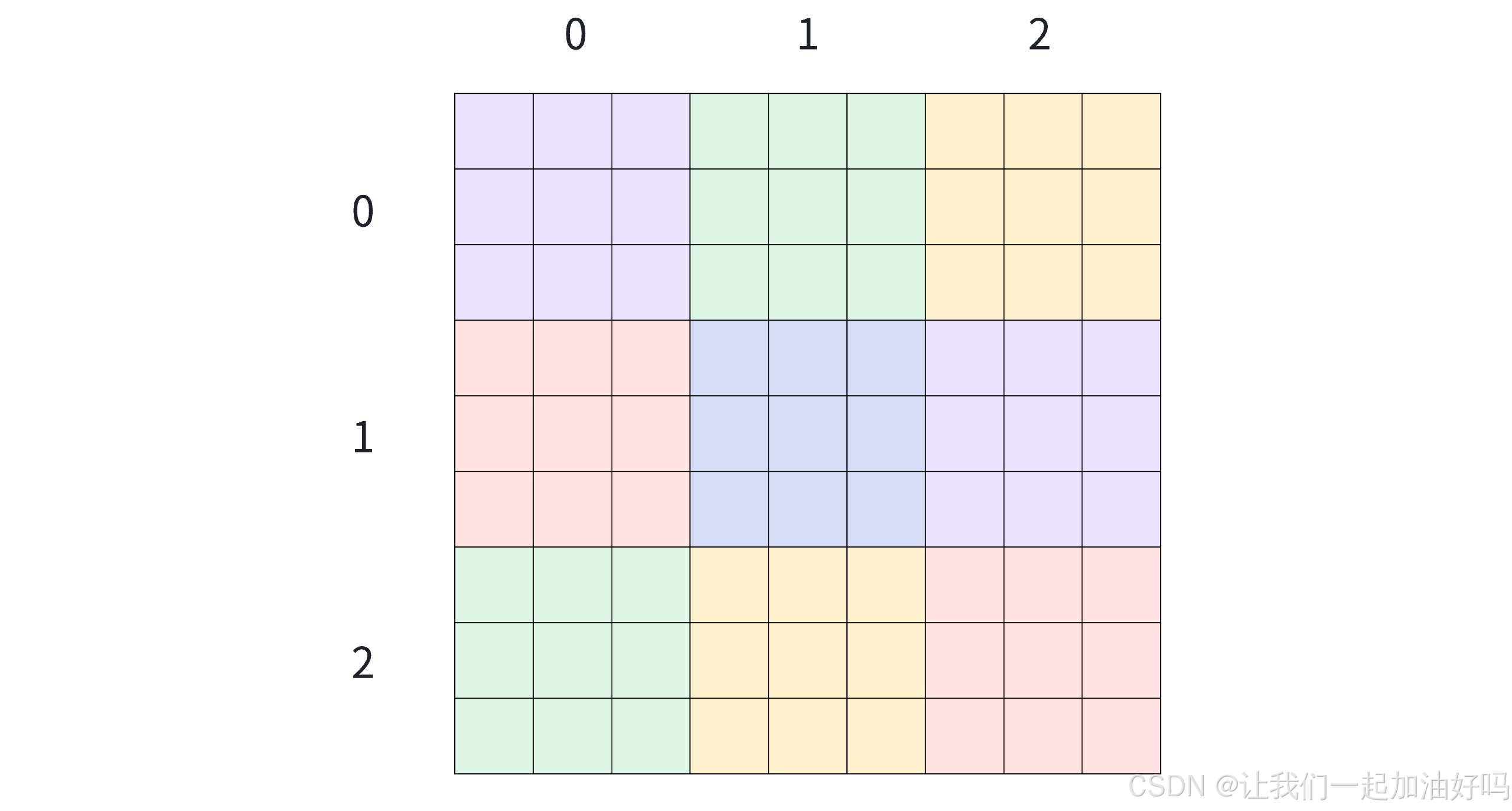
我们可以创建三个数组来依次判断行、列、 3 × 3 3\times3 3×3 方格内是否合法:
row[i][num] == true表示:第i行已经放上了num这个数;
col[j][num] == true表示:第j列已经放上了num这个数;
st[i / 3][j / 3][num] == true表示:[i / 3, j / 3]的 3 × 3 3\times3 3×3 方格里,已经放上了num这个数。为什么是
i / 3和j / 3?如果我们把第一行第一列的数记为[0, 0],那么在数独的最左上角的 3 × 3 3\times3 3×3 方格里的所有位置的坐标都满足[i / 3, j / 3] = [0, 0]。其他方格同理,也就是说我们可以把在同一个 3 × 3 3\times3 3×3 方格中的所有坐标映射成为同一个坐标,这样我们就可以判断同一个 3 × 3 3\times3 3×3 方格中是否存在某个数了。
(2) 代码实现
cpp
#include<iostream>
using namespace std;
const int N = 10;
const int M = 3;
int n = 9;
int mat[N][N];
bool row[N][N], col[N][N], st[M][M][N];
bool dfs(int i, int j)
{
// 如果当前列超了范围,就到下一行的第一个位置继续枚举
if(j == n)
{
i++;
j = 0;
}
// 如果当前行超了范围,说明我们把数独填完了,也就是找到了一种解,直接返回 true
if(i == n) return true;
// 如果下一行的第一个位置已经有数了,那么继续枚举下一个位置
if(mat[i][j]) return dfs(i, j + 1);
// 枚举 1~9 所有数
for(int x = 1; x <= n; x++)
{
// 如果当前位置合法
if(!row[i][x] && !col[j][x] && !st[i / 3][j / 3][x])
{
row[i][x] = col[j][x] = st[i / 3][j / 3][x] = true;
mat[i][j] = x;
if(dfs(i, j + 1)) return true; // 递归到下一层
// 如果这里不判断的话,那么这个 dfs 会把整个决策树遍历完,也就是说中途遇到了合法解它不会停下
// 所以这里判断一下返回 true 再配合上前面的if(i == n)那句就可以实现遇到一个合法的解就直接全部返回,不再枚举
// 这也是把 dfs 函数返回值设置为 bool 类型的意义
// 回溯,恢复现场
row[i][x] = col[j][x] = st[i / 3][j / 3][x] = false;
mat[i][j] = 0;
}
}
// 如果一直到循环结束都还没有返回 true,说明之前的某一个位置填错了,不是一个合法的解,返回 false
return false;
}
int main()
{
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
cin >> mat[i][j];
int x = mat[i][j];
// 如果当前位置不是 0 就标记一下
if(x) row[i][x] = col[j][x] = st[i / 3][j / 3][x] = true;
}
}
dfs(0, 0);
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
cout << mat[i][j] << " ";
}
cout << endl;
}
return 0;
}