多种二分查找

文章目录

二分查找

二分查找

常规实现

java 复制代码

public static int binarySearch(int[]a,int target)
{
    int i=0,j=a.length-1;
    while(i<=j)
    {
        int m=i+((j-i)>>>1);
        if(target<a[m])
        {
            j=m+1;
        }
        else if(a[m]<target)
        {
            i=m-1;
        }
        if(target==a[m])
        {
            return m;
        }
    }
    return -1;
}

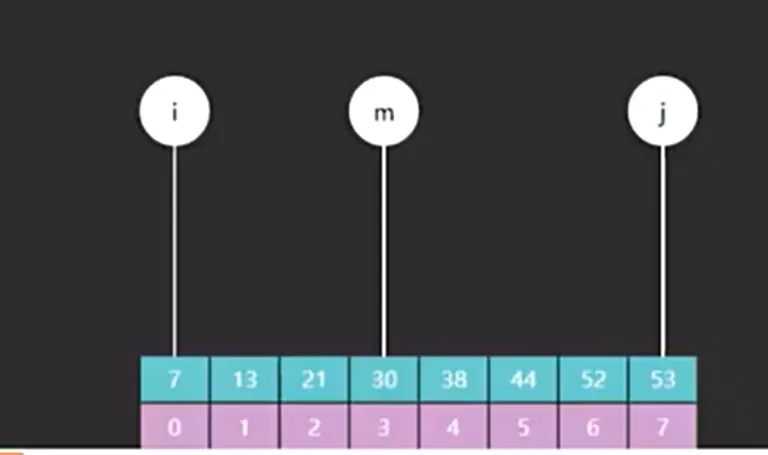
此时i和j所对应的元素都要参与比较运算，故循环条件为i<=j

改动版

java 复制代码

public static int binarySearch(int[]a,int target)
{
    int i=0,j=a.length;
    while(i<j)
    {
        int m=i+((j-i)>>>1);
        if(target<a[m])
        {
            j=m;
        }
        else if(a[m]<target)
        {
            i=m-1;
        }
        if(target==a[m])
        {
            return m;
        }
    }
    return -1;
}

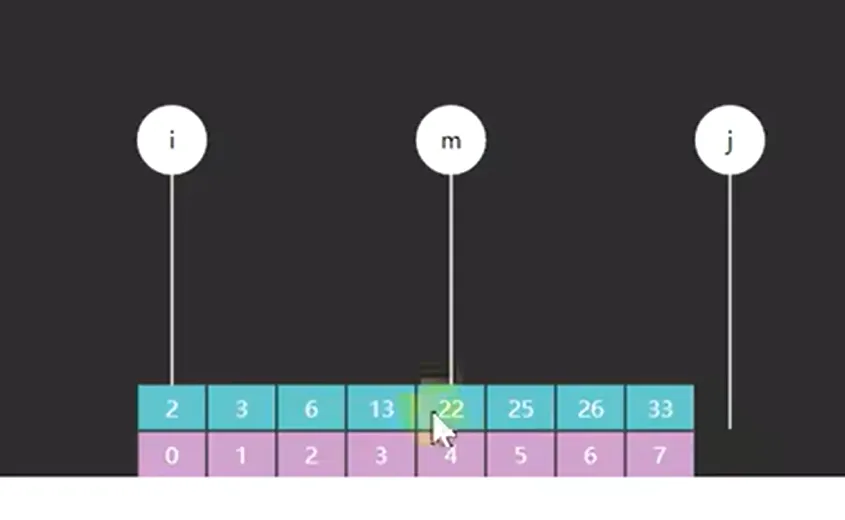
**此时j表示边界，j指向的并不是查找目标，故循环条件为i<j,且j=m

平衡版

改进之前二分查找左边和右边所用时间不一样的情况

特点：左闭右开的区间，i指向的可能是目标，而j指向的不是目标
不在循环内找出，等循环范围只剩i时，在循环外面比较a[i]与target

java 复制代码

public static int binarySearch(int[]a,int target)
{
    int i=0,j=a.length;
    while(1<j-i)
    {
        int m=i+((j-i)>>>1);
        if(target<a[m])
        {
            j=m;
        }
        else
        {
            i=m;
        }

    }
    if(target==a[i])
    {
        return i;
    }
    return -1;
}

java中直接用Arrays类下的binarySearch方法进行查找，如果找到了返回目标的索引，没找到返回-(插入位置索引+1)

有重复元素时查找与目标相等的最靠左的索引

java 复制代码

public static int binarySearch(int[]a,int target)
{
    int i=0,j=a.length-1;
    while(i<=j)
    {

        int m=i+((j-i)>>>1);
        if(target<=a[m])
        {
            j=m-1;
        }
       else
        {
           i=m+1;
        }
    }
  return i;
}

找到最右边的元素

java 复制代码

public static int binarySearch(int[]a,int target)
{
    int i=0,j=a.length-1;
    while(i<=j)
    {

        int m=i+((j-i)>>>1);
        if(target<a[m])
        {
            j=m-1;
        }
        else if(a[m]<=target)
        {
            i=m+1;
        }
    }
    return i-1;
}