目录
[1.1 位运算符号](#1.1 位运算符号)
[1.2 判断数n的第x位是0还是1](#1.2 判断数n的第x位是0还是1)
[1.3 修改数n的第x位为1](#1.3 修改数n的第x位为1)
[1.4 修改数n的第x位为0](#1.4 修改数n的第x位为0)
[1.5 提取一个数n二进制形式中最右侧的1](#1.5 提取一个数n二进制形式中最右侧的1)
[1.6 删去一个数n二进制形式中最右侧的1](#1.6 删去一个数n二进制形式中最右侧的1)
[1.7 异或（^）运算的规律](#1.7 异或（^）运算的规律)
[1.8 位图的思想](#1.8 位图的思想)
[2.1 面试题 01.01. 判定字符是否唯一](#2.1 面试题 01.01. 判定字符是否唯一)
[2.2 268. 丢失的数字](#2.2 268. 丢失的数字)
[2.3 371. 两整数之和](#2.3 371. 两整数之和)
[2.4 137. 只出现一次的数字 II](#2.4 137. 只出现一次的数字 II)
[2.5 面试题 17.19. 消失的两个数字](#2.5 面试题 17.19. 消失的两个数字)
一、基础的位运算
1.1 位运算符号
<< 左移：即将当前数的二进制形式整体向左移
eg：1 的二进制形式为：0000 0001
那么1<<2就是把1向左移动两位，即为0000 0100
>> 右移：即将当前数的二进制形式整体向右移eg：8的二进制形式为：0000 0100
那么1>>2就是把8向右移动两位，即为0000 0001
& 与操作：a & b就是a和b的每个二进制位进行与操作，同时为1则为1，出现0则为0eg: a=0110 1001
b=1100 0101
a & b=0100 0001
| 或操作：a | b就是把a和b的每个二进制位进行或操作，出现1则为1，同时为0则为0eg: a=0110 1001
b=1100 0101
a | b=1110 1101
~ 取反操作:即将当前数的每一个二进制位都进行取反操作，1变0,0变1eg: a=0110 1001
~a=1001 0110
^ 异或运算：a ^ b就是把a和b的每个二进制位进行异或操作，相同为0，不同则为1eg: a=0110 1001
b=1100 0101
a ^ b=1010 1100
🌟：这里重点注意一下：异或运算我们也可以称为是无进位加法运算，我们还是以a和b为例
a和b不算进位相加就是 1010 1100
可以看到不算进位相加的结果和异或运算的结果是相同的
1.2 判断数n的第x位是0还是1
我们已知一位二进制位和1相与之后，如果该位是0则得到0，是1则得到1。所以我们可以让我们想要获取的那位右移到最右边，再与1相与，我们就可以获取到这个位的值
eg： n=1001 1101
我现在想要获取数n的第3位的值，此时让n右移3位，得到0001 0011，此时和1相与。
n>>3 = 0001 0011
1 = 0000 0001
相与得到结果得到1，我们可以验证一下1001 1 101的第3位（从0开始计数），确实与答案相同。
1.3 修改数n的第x位为1
我们已知一位二进制位和1相或之后，都会得到1，与0相或之后，都会得到0。所以我们只要让该位和1相或，其他位与0相或即可。我们可以让1左移x位，就可以得到我们需要的数
eg： n=1001 1101
我现在想要修改数n的第5位的值为1，此时让1左移5位，得到0001 0000，此时与n相或。
n = 1001 1101
1<<5 = 0010 0000
相或后得到1011 1101，验证我们成功修改了第5位的值为1
1.4 修改数n的第x位为0
我们已知一位二进制位和0相与之后，都会得到0；与1相与之后，都会得到1。所以我们只要让x位与0相与，其他位与1相与即可得到答案。我们可以让1左移x位之后，再取反，即可得到我们需要的数。
eg： n=1001 1101
我现在想要修改数n的第2位的值为0，此时让1左移2位，得到0000 010，此时与n相或。
n = 1001 1101
1<<5 = 0010 0000
相或后得到1011 1101，验证我们成功修改了第5位的值为1
1.5 提取一个数n二进制形式中最右侧的1
我们提前要明白把一个数变成负数，就是把这个数的二进制取反再加1。此时这个负数的二进制形式就会形成，在右侧第一个1的左边与原数全部相反，这个1右侧的数全部为0。此时我们再让两个数相与，就会只保留最右侧的那个1
eg： n=1010 0100
取反：0101 1011
-n=0101 1100
n & -n=0000 0100
n和-n相与后，就只保留最右侧第一个1了
1.6 删去一个数n二进制形式中最右侧的1
当我们把一个数n减去1后，如果不够减就会向前面的二进制位借位，比如n=0100，n-1=0011，此时n-1这个数就会形成一个状态：最右侧1的左侧与原来的数完全相同，1位置和右侧的位置都与原来的数n相反。此时让两个数相与，就会把最右侧的1删去
eg： n=1010 1100
n-1=1010 1011
n & n-1 =1010 1000
n和n-1相与后，就删去右侧第一个1了
1.7 异或（^）运算的规律
a ^ 0 = a a和0相或，二进制为1与0相或后还是为1，二进制为0与0相或后还是0，所以保持不变，还是a
a ^ a = 0 a和a相或，每一位二进制位都是一样的，相或运算之后都为0
a ^ b ^ c = a ^ (b ^ c) 这个表达式说明了几个数进行相或运算是满足结合律交换律的 ，也就是不考虑顺序，这是我们之前提到过异或运算^是不进位相加，相加就是不考虑顺序的，所以很容易证明。
1.8 位图的思想
位图就是类似于哈希表，只不过哈希表我们一般是建立一个数组。而位图就是我们可以利用一个数的二进制位直接实现一个哈希表，例如**一个int类型的数有32位，那我们就可以把这个数当做一个32长度的哈希表数组，如果0位置有记录则让该位置为1，反之则为0。**这里我们就运用了我们之前学到的把某一位置为1的方法。我们之后会根据具体的题目来加深印象
二、算法题目
2.1面试题 01.01. 判定字符是否唯一
面试题 01.01. 判定字符是否唯一 - 力扣（LeetCode）
https://leetcode.cn/problems/is-unique-lcci/
这道题目非常简单，很明显我们可以采用哈希表来完成，并且因为字符串中只有小写字母，我们可以直接创建一个大小为26的整型数组充当哈希表，下标为0的位置标记'a'的个数，以此类推。
那么这题我们可以进行优化，我们之前提到位图的时候，就是讲到位图就是讲一个变量的二进制位当成哈希表。那么这题我们可以采用一个int整型变量，32位的二进制位我们只需要26位即可
其实我们还是采用哈希表的思想，只不过之前我们是针对数组来做，可以直接使用n[0]=1这样的方式来置为1，而现在是针对一个变量，将他的二进制位置为1。
java
class Solution {
public boolean isUnique(String astr) {
//位图的思想
//鸽巢原理先做优化
if (astr.length()>26) return false;
int flag=0;
for(char x:astr.toCharArray()){
//先查看当前字符是否存入
if((flag>>(x-'a')&1)==1) return false;
flag |=(1<<(x-'a'));
}
return true;
}
}这段代码我们还可以使用鸽巢原理先做判断进行一个优化，鸽巢原理我们举例来说就是，如果有13个人，那么这13个人中一定有人生日月份是相同的，因为月份只有12个，13个人中一定会有人相同。
- 那么这题利用鸽巢原理就是当字符串长度大于26，也就是大于小写字母的个数，那么一定会有字符相同不唯一，我们就可以直接返回false。
- 进入循环提取字符，我们采用flag>>(x-'a')&1来提取flag的第x-'a'位的具体值
- 如果为1则说明之前已经遇到过该字符，直接返回false；如果位0则说明之前没有遇到过该字符，我们采用 flag |=(1<<(x-'a'))来把flag的第x-'a'位置为1.
- 最后成功退出循环的话则说明没有重复字符，返回true。
2.2 268. 丢失的数字
268. 丢失的数字 - 力扣（LeetCode）https://leetcode.cn/problems/missing-number/description/
这题我们采用异或的思想，我们之前在异或运算中提到过，a^0=a,a^a=0,我们可以从这两个公式中得出，偶数个相同的数a异或运算会得到0，奇数个相同的数a异或运算会到的a，并且我们之前还提到异或运算是不考虑计算顺序的。所以这一题我们就可以利用让数组中的数和[ 0,n ]中的数全部异或在一起，那个消失的数因为只有奇数个就会留下。
java
class Solution {
public int missingNumber(int[] nums) {
int ret=0;
for(int x:nums){ //对数组中的每个数异或
ret^=x;
}
for(int i=0;i<=nums.length;i++){ //对[ 0,n ]的数异或
ret^=i;
}
return ret;
}
}2.3 371. 两整数之和
371. 两整数之和 - 力扣（LeetCode）https://leetcode.cn/problems/sum-of-two-integers/description/
计算两数之和但是不能使用+，-号，此时我们可以使用异或运算，我们之前提过异或运算就是无进位的加法运算，所以我们让a^b就是得到无进位的运算，但是我们知道加法是会出现进位，那我们该如何得到进位，我们以**a=0011 0101（53）,b=1001 0011（147）**为例，a+b的正确值应该是200
a^b=1010 0110
a+b的进位：0001 0001 我们只要让a^b和进位值异或也就是无进位相加，此时我们需要继续计算a^b和进位值的进位值，再次异或，直到进位值为0，此时说明没有进位了。
那么这个进位我们应该如何得到呢，我们观察一下，很容易就可以得到进位值就是a&b的值，而且我们知道1和1相加之后要进位，是使前面一位进位，所以我们还要把进位值向左移1位
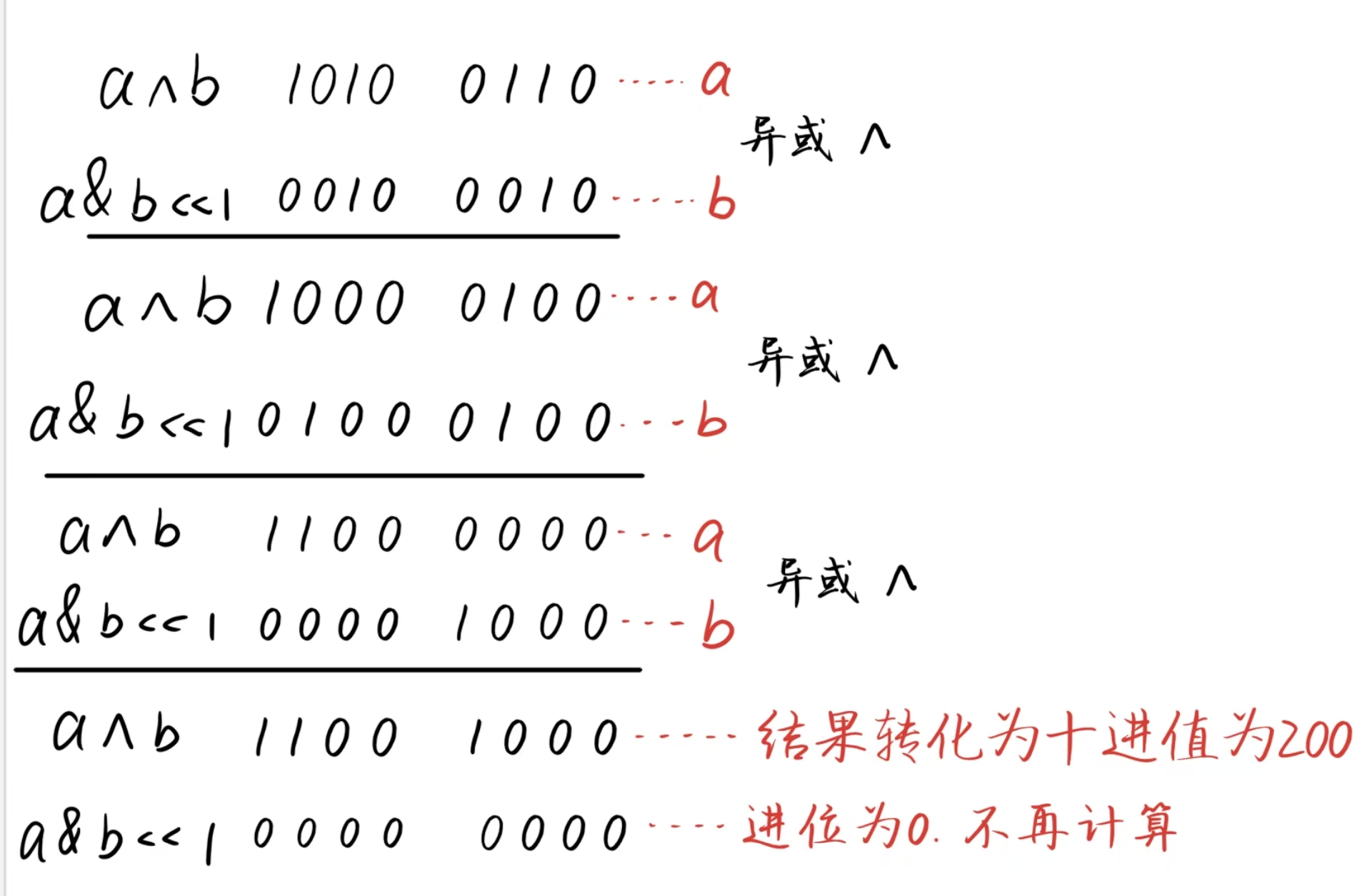
- 先让记录a^b（无进位相加）的结果
- 再记录a&b<<1（进位）的结果
- 进位不为0则继续异或
- 进位为0说明无进位，结束循环
java
class Solution {
public int getSum(int a, int b) {
while(b!=0){
int x=a^b; //记录无进位相加的值
int carry=(a&b)<<1; //记录进位的值
a=x;
b=carry;
}
return a;
}
}2.4 137. 只出现一次的数字 II
137. 只出现一次的数字 II - 力扣（LeetCode）https://leetcode.cn/problems/single-number-ii/description/
我刚看到题目想到的是通过异或运算得到结果，但是后来因为出现的次数都是奇数个，所以没有办法通过异或所有的数的出结果。这里我们换种角度考虑，我们把数分为两种，一种是出现一次的数，一种是出现三次的数，我们把出现一次的数记作a，挑出一个出现三次的数记作b。此时我们具体考虑到这一个a和三个b的具体二进制位，此时会出现4中情况
同一个二进制位会出现以下四种情况
- 3n个0 和 1个0
- 3n个0 和 1个1
- 3n个1 和 1个0
- 3n个1 和 1个1
此时我们针对一个二进制位来进行相加，再模3，我们就会发现规律：相加%3后得到的值就是我们只出现一次的那个数字的对应二进制的值，此时我们就可以遍历每一位二进制位，进行还原即可
java
class Solution {
public int singleNumber(int[] nums) {
int ret=0;
for(int i=0;i<32;i++){
//记录当前i位置的和
int sum=0;
for(int x:nums){
sum+=(x>>i)&1;
}
sum%=3;
if(sum==1) ret|=(1<<i);//如果sum%3的i位置为1，则把ret的i位置为1
}
return ret;
}
}2.5 面试题 17.19. 消失的两个数字
面试题 17.19. 消失的两个数字 - 力扣（LeetCode）https://leetcode.cn/problems/missing-two-lcci/description/
我们还是可以先尝试异或数组中的每个数字和[1,n+2]范围的数字，我们假设缺失的两个数字为a和b，此时我们异或的结果就是a^b ，此时只要我们可以把a和b分离出来即可
我们可以知道a和b肯定不相同，那么a^b的结果的二进制位一定是存在x位=1，这里的1指a和b的x位不相同，我们可以认为a的x位为0，b的x位为1。我们就可以把原来异或的数字分成两类，一类是x位为0的，一类是x位为1的，这样a和b就存在于不同的类了，又因为其他数可以互相抵消，最后留下来的就是a和b了
java
class Solution {
public int[] missingTwo(int[] nums) {
//把所有的数字异或在一起
int tmp=0;
for(int x:nums){
tmp^=x;
}
for(int i=1;i<=nums.length+2;i++){
tmp^=i;
}
//此时tmp=a^b，我们要找到tmp中为1的那一位,用diff记录
int diff=0;
while(true){
if(((tmp>>diff)&1)==1) break;
else diff++;
}
//此时diff位为1，我们将原来的数分为两类异或
//一类是diff位为1的，一类是diff位为0的
//因为除去消失的两个数字，nums里的数字都会因为是偶数个而抵消
//最后只会留下我们想要的数字
int[] ret=new int[2];
for(int x:nums){
if(((x>>diff)&1)==1) ret[0]^=x;
else ret[1]^=x;
}
for(int i=1;i<=nums.length+2;i++){
if(((i>>diff)&1)==1) ret[0]^=i;
else ret[1]^=i;
}
return ret;
}
}