LLM 确定性推理

可重复性是科学进步的基石。然而，从大语言模型中获得可重复的结果非常困难。例如：当你多次向 DeekSeek 询问同样的问题时，会产生不同的结果。这本身并不奇怪，因为从语言模型获得结果时涉及"采样"，这是一个将语言模型的输出转换为概率分布并概率选择词元的过程。

当我们将温度调低到 0，即贪婪采样（LLM 总是选择最高概率的词元），从而使采样在理论上具有确定性，但是 LLM API 在实践中仍然不是确定性的。

本文将介绍 LLM 批次推理确定性（一致性）的定义，产生批次推理不一致的原因，如何缓解批次推理不一致，以及业界最新的进展。

文章较长，建议先点赞收藏，再慢慢观看。另外，我撰写的大模型相关的博客及配套代码 均整理放置在Github：llm-action，有需要的朋友自取。

批次推理一致性定义

LLM批次推理一致性指的是：在批次推理（一次处理多个输入）的场景下，LLM对于完全相同的输入，无论其在批次中的位置、批次的大小或并发的环境中，都能够产生完全相同的输出结果。

简单来说，就是确保批次处理的结果是确定性的和可重现的。

为什么需要关注批次推理的一致性？

批次推理是提高 LLM 服务吞吐量、降低单位成本的关键技术。但在追求效率的同时，必须保证结果的质量和可靠性。因为，不一致性可能会带来严重问题：

• 调试困难：如果同一个问题在不同时间或不同批次中得到不同答案，将会影响可重现性，开发者将难以定位是模型、数据还是系统的问题。而可重现性是科学进步的基石。
• 用户体验差：用户期望相同的提问得到稳定的回答。不一致的回答会损害用户对产品可靠性的信任。例如：在医疗、法律、金融等对准确性和可靠性要求极高的高风险领域，LLM 推理不确定性可能引发严重后果。
• 公平性问题：在需要对多个项目进行排序或评分的场景（如简历筛选、内容审核），不一致的评判标准会导致不公平的结果。
• 流水线中断：下游应用程序可能依赖于LLM输出的特定格式或内容，不一致的输出可能导致后续处理流程崩溃。

业界现状

MAAS平台

目前，市面上知名 MAAS 平台（比如：OpenAI、Kimi、DeepSeek、Qwen、火山引擎等），相同输入基本都是不一样的输出内容，且大多都没有暴露出控制一致性的参数。

开源工具

当下，大多数开源推理框架（比如：SLang、vLLM、LMDeploy）同样存在批次推理不一致的问题。

批次推理产生不一致的原因

LLM 推理的计算过程本质上就是浮点数运算（矩阵乘或者Element-Wise操作）+ 随机因素的组合。只要控制住浮点运算过程一致性和随机一致性，就可以保证结果一致性。而LLM批次推理过程中破坏一致性的常见原因有：

1. 非确定性算法：即使设置了 temperature=0，底层GPU的并行计算可能因计算顺序不同而导致微小的数值差异，经过模型的多层传播后，最终可能表现为不同的输出token。
2. 浮点数精度：使用不同的精度（如FP32, FP16, BF16）可能会因舍入误差导致不同的结果。
3. 注意力机制：某些注意力实现（如FlashAttention）为了优化性能，可能会引入非确定性。
4. 资源竞争和并行化：高度并行的系统中，线程或进程的调度顺序可能影响计算结果。
5. 不同批次推理大小：由于现有的kernel实现（比如：RMSNorm、MMA、Attention）不是批处理不变的，因此，不同批次推理大小导致计算图结构变化（如矩阵并行的分块方式），导致中间层激活值不同，最终输出分歧。

伪随机

在计算机中，伪随机数由数学算法生成，初始值（随机种子）确定后，序列完全可复现。虽然表面看似随机，但本质是确定性的。

也就是说，只要控制住随机种子，就能够保证计算过程中，随机因素的一致性。如下所示，相同随机种子下，随机生成的内容是一致的。

In [1]: import numpy as np
   ...:
   ...: N = 10
   ...: seed_1 = 42
   ...: seed_2 = 100
   ...: np.random.seed(seed_1)
   ...: arr1 = np.random.randn(N)
   ...: np.random.seed(seed_2)
   ...: arr2 = np.random.randn(N)
   ...: np.random.seed(seed_1)
   ...: arr3 = np.random.randn(N)


In [2]: arr1 == arr2
Out[2]:
array([False, False, False, False, False, False, False, False, False, False])


In [3]: arr1 == arr3
Out[3]:
array([ True,  True,  True,  True,  True,  True,  True,  True,  True, True])

浮点计算过程

1. 计算输入内容因素

如果计算的输入不一致，即使相同的计算逻辑，最终的输出应该会不一致，即当 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 ≠ x 2 x_1 \neq x_2 </math>x1=x2，则 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x 1 ) ≠ f ( x 2 ) f(x_1) \neq f(x_2) </math>f(x1)=f(x2)。例如，推理时，模型输入不一致、模型参数不一致、相同模型量化精度不一致，都会导致推理结果不一致，输出采样不一致。

2. 计算顺序因素

在计算机浮点运算中，浮点数计算顺序也会导致结果不一致，最简单的例子就是浮点数加法满足交换律，但不一定满足结合律，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 + x 2 + x 3 ≠ x 1 + ( x 2 + x 3 ) x_1 + x_2 + x_3 \ne x_1 + (x_2 + x_3) </math>x1+x2+x3=x1+(x2+x3)。具体示例如下：

(0.1 + 1e20) - 1e20
>>> 0
0.1 + (1e20 - 1e20)
>>> 0.1

其实这是计算机底层原理导致的。因为要表示一个浮点数，精度是有限的，再加上舍入误差，就导致不同运算顺序会产生不同结果。

在推理中，一些优化技巧（比如：算子融合），会改变计算顺序，虽然数学上计算应该是一致的，但在计算机中，计算结果不一致。

因此，要保证计算一致性，必须要求计算顺序严格一致。

3. 计算函数实现因素

在实际计算任务中，不同环境下，即使调用相同库的某个函数，相同输入也不能保证输出一致，因为计算环境中的软件、硬件版本不一致。例如：CUDA矩阵乘算子GEMM，这个算子的具体实现受当前GPU架构（如Hopper、Ampere）、CUDA版本等因素的影响，导致实际浮点计算顺序不一致，因此，最终结果不一致。示例代码如下：

import torch

torch.cuda.manual_seed(1)

N, K, M = 256, 512, 4096
A = torch.randn(N, K, device='cuda')
B = torch.randn(K, N, device='cuda')

C = torch.mm(A, B).sum()

# 在torch版本2.3.1+cu121， RTX4090下，执行结果C为 -3701.7944
# 在torch版本2.8.0+cu128， H200下，   执行结果C为 -3701.7949
# 结果最后一位略有差异

由于相同的计算函数，不同的实现有正确性保证，因此结果差异会很小。但在计算链路非常长的场景下，如长文本推理，这个差异会被逐步放大，最终可能导致呈现的结果有差异。

批次不变性缺失

浮点计算过程是产生不一致输出的根本原因，但它并未直接回答不确定性源自何处。它无法帮助我们理解：浮点数值为何会以不同顺序相加，这种情况何时会发生以及如何避免这种情况。

在 LLM 推理中，Kernel（如矩阵乘法、RMSNorm、注意力机制）虽具备 「运行间确定性」（即相同输入多次运行结果一致），但缺乏 「批次不变性」。当批处理大小变化时，单个批次中的元素的计算结果会改变。

然而，推理服务器的负载（即决定批处理大小）对用户而言是随机变量，批处理大小变化导致同一请求在不同负载下输出不同，最终表现为非确定性。这一问题不仅存在于 GPU，在 CPU、TPU 上同样存在。

缓解批次推理不一致的方案

在某些业务场景下，对LLM模型输出返回有强一致性的要求，需要通过特殊的配置和技术方案实现输出一致性。然而，推理引擎的一些优化技术，会影响输出一致性，去除这些优化技术，会大大降低推理的效率，从而导致推理成本变高。因此，需要根据具体业务场景进行一些取舍。

以下是一些缓解批次推理不一致的配置：

业界最新进展

Thinking Machines Lab 发布了导致 LLM 批次推理输出不一致的真凶，并提出一套能够在将温度设为0时输出完全一致的解决方案。并通过vLLM 进行了概念验证。而 SGLang 快速针对 Thinking Machines Lab 发布的 batch-invariant kernels 进行了集成和优化。

Batch Invariant Ops

参考：

• thinkingmachines.ai/blog/defeat...
• github.com/thinking-ma...

该方案提到导致 LLM 批次推理输出不一致的原罪是浮点的非结合性。此外，LLM 中，Kernel 不具备不变性的原因是由于批次大小的不确定（即服务器承受的负载）。因此，如果想在推理服务器中避免不确定性，必须在 Kernel 中实现批次不变性。

如何使Kernel保持批次不变性（batch-invariant）？

为了使 Transformer 实现 batch-invariant，必须使每个内核都 batch-invariant。幸运的是，我们可以假设每个逐点算子都是批次不变的。

因此，我们只需要关注涉及归约（reductions）的 3 个算子 ------ RMSNorm、矩阵乘法和注意力。每个算子都需要一些额外的考虑因素，以实现具有合理性能的批次不变性。

1. 批次不变的RMSNorm

批次不变性的要求是无论kernel的批处理大小如何，每个元素的归约顺序都必须是固定的 。但这并不意味着必须始终使用相同的归约策略。例如，如果我们更改要归约的元素数量，即使我们的归约策略发生变化，仍然可以是批次不变的。因此，只有当我们的批次大小影响策略策略时，我们才会破坏批次不变性。

通常，并行算法受益于最大限度地减少跨内核的通信。因此，一种策略是将每个批次的元素分配给一个内核，如下图所示，这是普通的 RMSNorm 并行策略

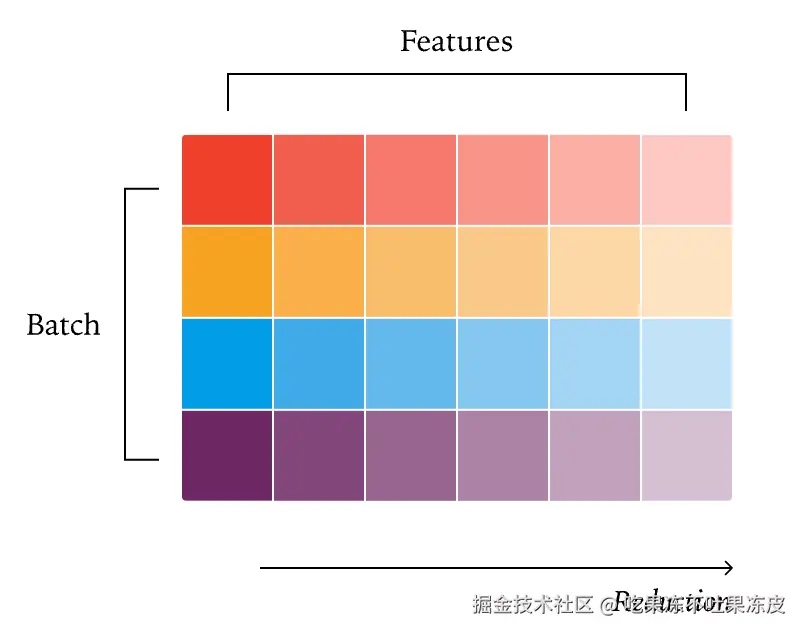
数据并行 RMSNorm：理想情况下，我们希望在并行策略中避免核心（core，即 SM）间的通信。实现这一目标的一种方法是为每个核心分配一个批次元素，从而保证每个归约完全在单个核心内完成。这就是所谓的「数据并行」策略，因为我们只是沿着一个不需要通信的维度进行并行化。在这个例子中，我们有四行和四个核心，从而使我们的核心饱和。

此外，增加我们的批次大小不会影响我们的归约策略；如果 200 的批次大小为我们的 Kernel 提供了足够的并行性，那么 2000 的批次大小肯定会提供足够的并行性。

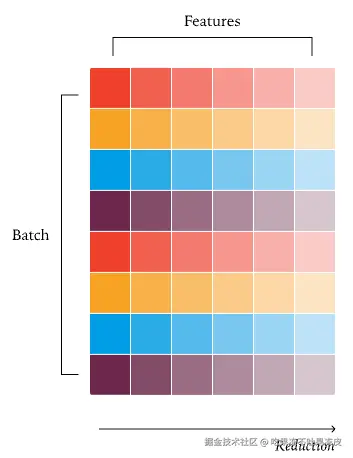
用于更大批次的数据并行 RMSNorm：将数据并行策略扩展到更大的批次相当直接，与其让每个核心处理一行，不如让每个核心顺序处理不同的行。这保留了批次不变性，因为每个批次元素的归约策略保持不变。

另一方面，减小批次大小可能会带来挑战。因为我们为每个批次的元素分配一个核心，减小我们的批次大小最终会导致核心数多于批次元素数，使一些核心闲置。

遇到这种情况，一个优秀的 Kernel 工程师会采用的解决方案之一（原子加法或拆分归约），以保持良好的并行性和性能。不幸的是，这改变了归约策略，阻止了这个 Kernel 实现批次不变性。

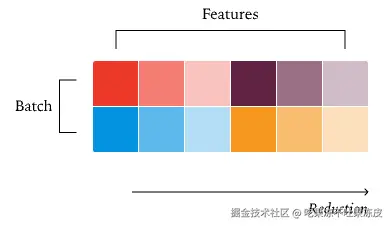
拆分归约 RMSNorm ：如果我们的批次大小很小，我们的数据并行策略可能不再有足够的并行性来使我们的核心饱和。在这种情况下，将一个归约「拆分」到多个核心之间可能更高效，让我们能够充分利用我们的 GPU。然而，这会失去批次不变性，因为我们不再以相同的顺序对每个元素进行归约。

最简单的解决方案是完全忽略这些情况。这并非完全不合理。原因是小的批次大小意味着 Kernel 很可能执行得很快，因此，性能下降可能不是灾难性的。

如果我们必须优化这个用例，一种方法是始终使用一种即使对于非常小的批次大小也具有足够并行性的归约策略。这样的归约策略对于较大的批次大小会导致过多的并行性，但能让在整个尺寸范围内实现不错（但非最佳）的性能。

2. 批次不变的矩阵乘

在其核心中，你也可以将矩阵乘法看作是一个逐点操作后跟一个归约操作。然后，如果我们通过将输出分块为 tile 来并行化我们的矩阵乘法，我们就有了一个类似的「数据并行」Kernel 策略，它将每个归约保持在一个核心内。

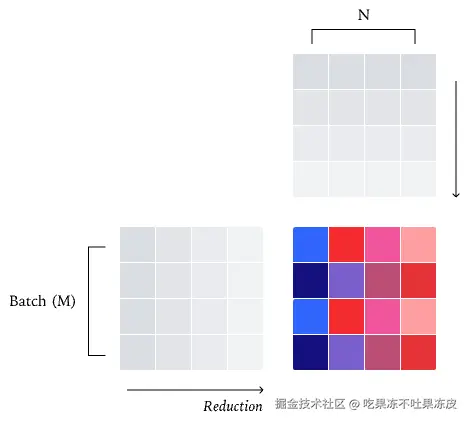
数据并行 Matmul：与 RMSNorm 类似，矩阵乘法的标准并行化策略是一种「数据并行」策略，将整个归约保持在一个核心内。最直接的思考方式是将输出张量拆分成二维的 tile，并将每个 tile 分配给一个不同的核心。每个核心然后计算属于该 tile 的点积，再次在单个核心内执行整个归约。与 RMSNorm 不同，围绕算术强度和利用 tensor cores 的额外限制迫使我们拆分二维 tile 而不是单个输出元素，以实现高效的 matmul Kernel。

也与 RMSNorm 类似，「批次」维度（M 和 N）可能会变得太小，迫使我们沿着归约维度（K）进行拆分。尽管有两个「批次」维度，矩阵乘法也要求我们每个核心有更多的「工作量」，以便有效地利用 Tensor Cores。例如，如果你有一个 [1024, K] x [K, 1024] 的矩阵乘法和一个标准的二维 tile 大小 [128, 128]，数据并行策略只能将这个矩阵乘法拆分到 64 个核心，不足以使 GPU 饱和。 在矩阵乘法中沿归约维度进行拆分被称为 Split-K Matmul。就像 RMSNorm 一样，使用这种策略会破坏批次不变性。

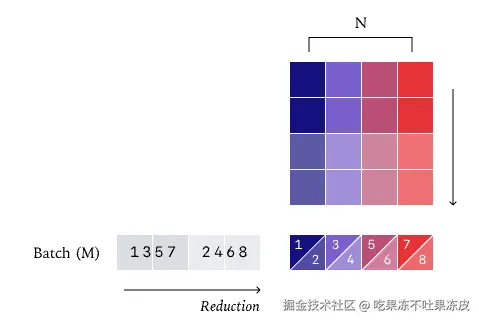
Split-K Matmul 如果我们的批次维度相当小，我们可能没有足够的并行性，需要一个 split-k matmul。在这个例子中，我们将每个归约拆分到两个核心，它们将分别累加，然后在最后合并它们的结果。然而，将每个归约拆分到两个核心，使我们仍然能够利用八个核心。

此外，还有一个额外的复杂性------tensor core 指令。对于归约，我们可以简单地一次处理一行，而高效的矩阵乘法 Kernel 必须一次处理一个完整的「tile」。

每个 tensor-core 指令（比如：wgmma.mma_async.sync.aligned.m64n128k16）内部可能有不同的归约顺序。使用不同 tensor-core 指令的一个原因可能是批次大小非常小。例如，如果我们使用一个处理长度为 256 的 tile 的 tensor-core PTX 指令，但批次大小只有 32，我们几乎浪费了所有的计算！在批次大小为 1 时，最快的 Kernel 通常根本不使用 tensor core。

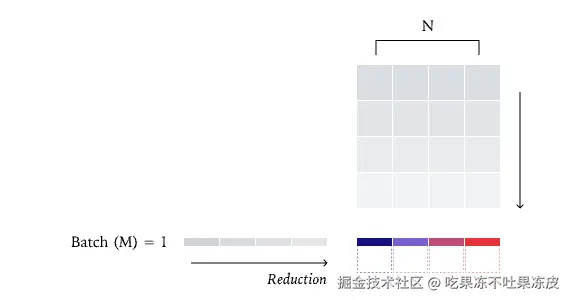
填充的 Tensor-Core 指令：如果批次大小太小，我们可能会遇到一种情况，即输出中连一个二维 tile 都放不下。在这种情况下，最高效的做法是切换到一个更小的 tensor-core 指令，或者完全不使用 tensor-core！然而，这两种选择都阻止了我们的 Kernel 实现批次不变性。

所以，确保矩阵乘法批次不变性的最简单方法是编译一个 Kernel 配置，并将其用于所有形状。虽然我们会损失一些性能，但这在 LLM 推理中通常不是灾难性的。特别是，当 M 和 N 都很小时，最需要 split-k，而幸运的是，在我们的情况下，N（即模型维度）通常相当大！

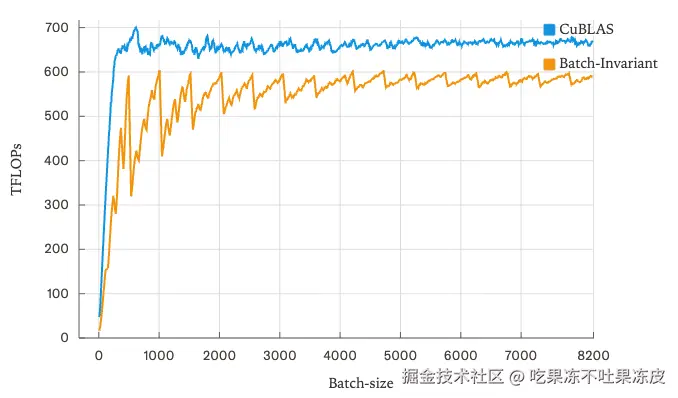
尽管实现批次不变性，相比 cuBLAS 只损失了大约 20% 的性能。同时，这也不是一个优化的 Triton Kernel (例如，没有 TMA)。然而，性能中的一些模式说明了批次不变性在何处损失了性能。首先，由于指令过大和并行性不足，我们在非常小的批次大小时损失了大量性能。其次，随着批次大小的增加，存在一个由量化效应（包括tile和wave）引起的「拼图」模式，这通常通过改变 tile 大小来缓解。

3. 批次不变的注意力

在为矩阵乘法实现批次不变性之后，Attention 引入了两个额外的难题，因为它包含两个矩阵乘法。

• 与 RMSNorm 和矩阵乘法仅在特征维度上进行归约不同，我们现在在特征维度 和序列维度上进行归约。
• 由于上述原因，Attention 必须处理各种影响序列处理方式的推理优化（分块预填充、前缀缓存等）。

因此，为了在 LLM 推理中实现确定性，我们的数值必须对一次处理多少个请求 以及每个请求在推理引擎中如何被切分保持不变。

首先，让我们看一遍 Attention 的标准并行策略，该策略首次在 FlashAttention2 中引入。与 RMSNorm 和 Matmul 类似，默认策略是「数据并行」策略。由于我们沿 key/value 张量进行归约，数据并行策略只能沿 query 张量进行并行化。

例如：根据推理引擎的选择，一个序列可能会被分成几个部分处理 （例如：在分块预填充中），或者可能一次性全部处理（如果预填充没有被分割）。为了实现「批次不变性」，给定 token 的归约顺序必须不依赖于其序列中同时处理的其他 token 的数量。如果你像 vLLM 的 Triton attention kernel 那样，将 KV 缓存中的 K/V 值与当前正在处理的 token 中的 K/V 值分开进行归约，这是无法实现的。例如：在处理序列中的第 1000 个 query token 时，无论 KV 缓存中有 0 个 token（预填充）还是 999 个 token（解码），归约顺序都必须相同。

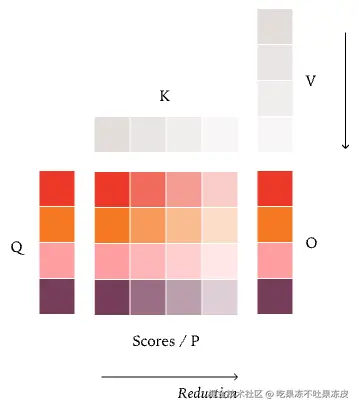
FlashAttention2 策略：我们沿着 Q 进行并行化，并同时沿着 K/V 进行归约。这意味着我们的整个归约可以保持在单个核心内，使其成为另一种数据并行策略。

为了解决这个问题，我们可以就在 attention kernel 本身之前更新 KV 缓存和页表，确保无论正在处理多少个 token，我们的 key 和 value 始终以一致的方式布局。

有了这个额外的细节（以及前一节提到的所有事项，如一致的 tile 大小），我们就能实现一个批次不变的 attention 实现！

然而，这里有一个重要问题。与矩阵乘法不同，我们在 LLM 推理中看到的 attention 形状通常确实需要一个拆分归约的 Kernel，通常称为 Split-KV 或 FlashDecoding。这是因为如果我们不沿归约维度进行并行化，我们只能沿批次维度、头维度和「query 长度」维度进行并行化。在 attention 的解码阶段，query 长度非常小，因此，除非我们有非常大的批次大小，否则我们通常无法使 GPU 饱和。

遗憾的是，要忽略这种情况并不像对 RMSNorm 和 Matmul 那样容易。例如，如果你有一个非常长的 KV 缓存，attention kernel 可能会花费很长时间，尽管只处理一个请求。

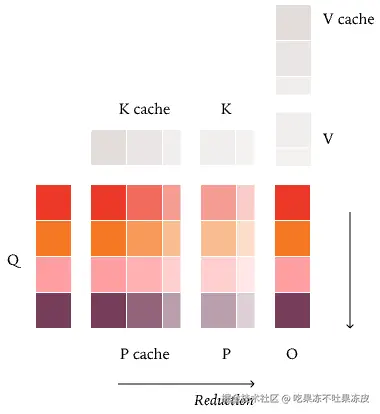
带 KV 缓存的 FlashAttention：为什么将 KV 缓存与当前 KV 值分开处理会破坏批次不变性，原因有点微妙，与「边界条件」有关 。具体来说，假设你的块大小是 32，但我们当前 KV 缓存中有 80 个元素。然后我们计算了另外 48 个未缓存的元素。在这种情况下，我们需要三个块（两个完整的和一个掩码的）来计算「P cache」，另外两个块（一个完整的和一个掩码的）来计算「P」。因此，当我们总共只有四个块（即 128）的元素需要计算时，却需要五个块来完成我们的归约，这肯定会改变我们的归约顺序。例如：如果我们反过来在 KV 缓存中没有元素，并且一次性处理 128 个元素，我们需要在这两种情况下获得相同的数值，以确保 Attention 的「批次不变性」。

此外，通常用于 attention 的拆分归约策略也对批次不变性构成了挑战。例如，FlashInfer 的「平衡调度算法」选择能够使 GPU 所有核心饱和的最大拆分大小，从而使得归约策略不是「批次不变的」。然而，与 RMSNorm/Matmul 不同，无论批次大小如何，选择一个固定的拆分数量是不够的。

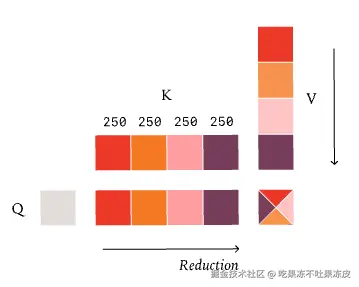
Fixed Split-KV 策略 (即 FlashDecode)：如果我们的 query 长度变得非常小（就像在解码期间那样），我们可能会陷入一种情况，即我们的 Kernel 中几乎没有并行性。在这些情况下，我们需要再次沿归约维度进行拆分------这次是 KV 维度。如何拆分 KV 维度的典型策略是计算出我们需要的并行度，然后均匀地划分 KV 维度。例如：如果我们的 KV 长度是 1000，我们需要 4 次拆分，每个核心将处理 250 个元素。遗憾的是，这也破坏了批次不变性，因为我们精确的归约策略取决于我们在任何给定请求中处理序列中的多少个 query token。

相反，为了实现批次不变性，我们必须采用一种「固定拆分大小」的策略。换句话说，我们不是固定拆分的数量，而是固定每次拆分的大小，最终得到一个可变数量的拆分。通过这种方式，我们可以保证无论我们正在处理多少个 token，我们总是执行相同的归约顺序。

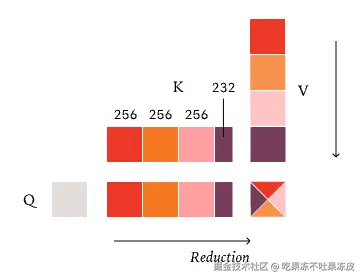
Fixed Size Split-KV 策略：这个策略和前一个策略唯一的区别是我们的拆分现在是「固定大小」的。例如：如果我们的 KV 长度是 1000，我们不会将其拆分为四个长度为 250 的均匀拆分，而是会将其拆分为三个固定大小长度为 256 的拆分和一个长度为 232 的拆分。这使我们能够保持批次不变性，因为我们的归约策略不再依赖于我们一次处理多少个 query token！

实现：

利用 vLLM 的 FlexAttention 后端提供了基于 vLLM 的确定性推理。同时，以一种非侵入式的方式替换大多数相关的 PyTorch 算子。

LLM 推理的非确定性统计：

为了量化 LLM 推理的非确定性程度，作者进行了一项实验：使用 Qwen/Qwen3-235B-A22B-Instruct-2507 模型，在温度设置为 0 的条件下，对相同的提示词（非思维模式）进行 1000 次补全采样，每次生成 1000 个 token。令人惊讶的是，即便在理论上应该确定性的设置下，仍然得到了 80 个独特的补全结果，其中最常见的补全出现了 78 次。

深入分析这些差异，作者发现补全结果在前 102 个 token 中是完全相同的！分歧首次出现在第 103 个 token。所有补全都始于"Feynman was born on May 11, 1918, in"，但其中 992 个补全继续生成"Queens, New York"，而另外 8 个补全则生成了"New York City"。这种细微但关键的差异，足以影响下游应用。

然而，当作者启用开发的批处理不变内核后，所有 1000 个补全结果都变得完全一致。这正是在数学上对采样器所期望的确定性行为，也验证了批处理不变内核在消除不确定性方面的有效性。

推理性能：

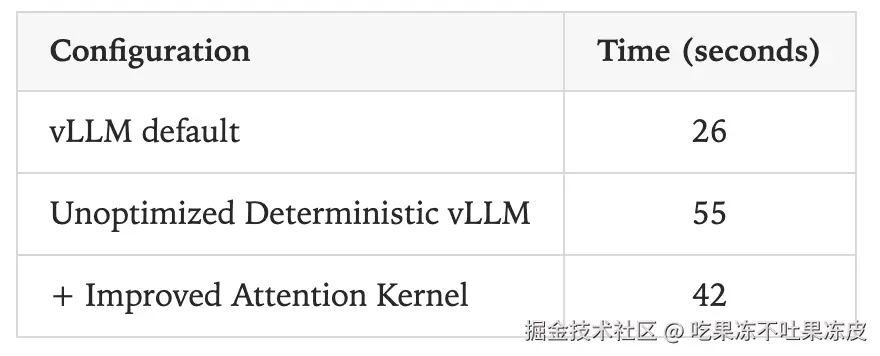
针对 Qwen-3-8B，并请求 1000 个输出长度在 90 到 110 之间的序列。 结论：性能下降约61.5%，速度下降的大部分原因是 vLLM 中的 FlexAttention 集成尚未得到大量优化。

Enabling Deterministic Inference for SGLang

参考：

• lmsys.org/blog/2025-0...

由于不同的批量大小会影响内核的归约分割过程。这会导致每个归约块的顺序和大小发生变化，由于浮点运算的非关联性，这可能会导致不确定的输出。为了解决这个问题，Thinking Machines Lab用批次不变的实现替换了归约内核（RMSNorm、矩阵乘法、注意力等）。

基于 Thinking Machines Lab 的工作，SGLang 为确定性 LLM 推理提供了强大的高吞吐的解决方案，将批次不变的内核、CUDA 图、基数缓存和分块预填充结合，实现高效性能。并且SGLang的确定性推理已经通过综合测试和 RL 训练实验得到了广泛的验证。主要增强功能包括：

• 集成了 Thinking Machines Lab 的批次不变的内核 ，包括均 mean, log-softmax 和 matrix multiplication kernels
• 实现基于固定 KV 大小分割的批次不变注意力核。支持多个后端，包括 FlashInfer、FlashAttention 3 和 Triton。
• 与常见的推理功能完全兼容，例如：分块预填充、CUDA 图、基数缓存，所有这些功能在启用确定性推理时仍然受支持。
• 在采样参数中公开每个请求的种子 ，允许用户即使在温度 > 0 时也能启用确定性推理。
• 更好的性能 ：与 Thinking Machines Lab 博客中报告的 61.5% 的性能下降相比，SGLang 在 FlashInfer 和 FlashAttention 3 后端的性能平均下降仅为 34.35%， 这是一个显着的改进。使用 CUDA 图，与最小化的集成相比，可以实现 2.8 倍的加速。

技术细节：

1. 分块预填充

SGLang 的分块预填充技术旨在管理具有长上下文的请求。然而，其默认的分块策略违反了注意力核的确定性要求。

如图所示，考虑两个输入序列，seq_a 和 seq_b，每个输入序列的上下文长度为 6,000。分块预填充的最大块大小为 8192，而确定性注意力所需的拆分 KV 的大小为 2,048。每个序列可以划分为三个较小的单元（a1 到 a3 和 b1 到 b3），长度分别为 2,048、2,048 和 1,904。如果这些较小的单元在块预填充期间保持完整，那么它们可以由相同的注意力内核处理并导致确定性归约行为。

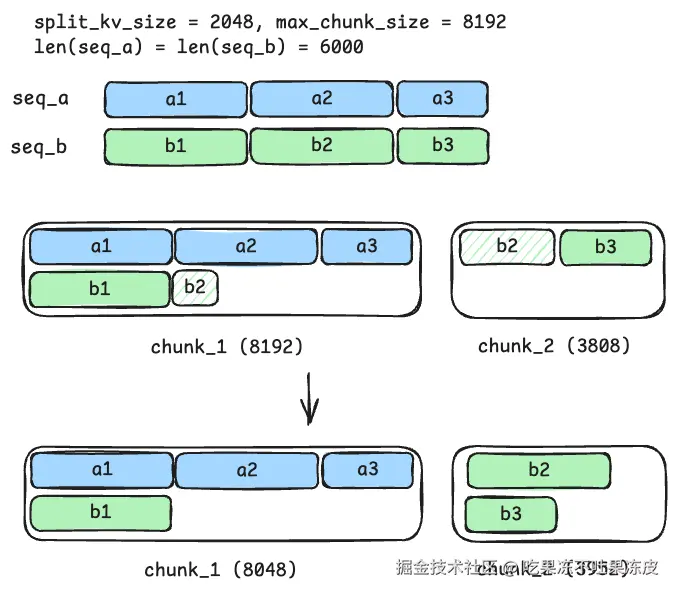
标准分块策略遵循"尽力而为"的原则。在此示例中，此策略尝试通过将 seq_b 的 b2 单位分成两个较小的部分来生成 8,192 个token的 chunk_1。这可能会导致截断点不一致，因为拆分后 b2 的长度取决于 seq_a 的长度。为了解决这个问题，我们调整了分块逻辑，使截断点与 split_kv_size 的整数倍对齐 。这种调整确保了 b2 的处理被推迟到后续块，从而允许注意力内核将其作为一个完整的单元进行计算。

2. Attention 后端

注意力内核是确定性的重要组成部分。对于不同的注意力后端，我们进行了不同的修改，以满足其使用需求。

• 对于 Flashinfer 后端，我们利用来自批次不变 FA2 内核的 fixed_split_size 和 disable_kv_split 参数来修复内核规划期间的拆分大小。分块预填充的截断与预填充拆分大小对齐。
• 对于 FlashAttention-3 后端，flash attention 内核的 num-split 固定为 1，以确保确定性。
• 对于 Triton 后端，我们固定解码的拆分大小，并手动设置分块预填充的对齐大小。确定性推理也可以在具有 Triton 后端可扩展性的 AMD 硬件上运行。

3. 可复现的非贪婪采样

为了将确定性扩展到贪婪解码之外，我们引入了一个新的采样函数：multinomial_with_seed。

在批处理条件下，torch.multinomial 本身就具有非确定性，而这一算子并不依赖 torch.multinomial，而是利用种子哈希函数产生的 Gumbel 噪声对 logits 进行扰动。因此，即使温度大于 0，相同的 (inputs, seed) 对总是产生相同的样本。

这一修改实现了确定性多项式采样，同时保留了强化学习rollout所需的随机性。

4. RL 框架集成（slime）

将温度 > 0 的确定性推理集成到 slime 的 GRPO 训练方案中。初步实验，重复的 RL 训练运行在第一次迭代中产生了相同的rollout响应和损失值 ，证实了rollout过程本身是确定性的。

后续将通过实施以下关键配置进一步实现了完整的训练可重复性：

• Flash Attention：使用 Flash Attention v2 而不是 v3 来启用确定性反向传播。
• Megatron：设置 --deterministic-mode 标识进行确定性训练
• 环境变量：配置关键设置：
  • NCCL_ALGO=Ring
  • NVTE_ALLOW_NONDETERMINISTIC_ALGO=0
  • CUBLAS_WORKSPACE_CONFIG=:4096:8
• PyTorch：启用 torch.use_deterministic_algorithms(True, warn_only=False)

通过这些全面的改变，成功地实现了slime中 使用 GRPO 训练完全可重复性，从而实现了真正确定性的端到端 RL 训练流水线。

推理性能：

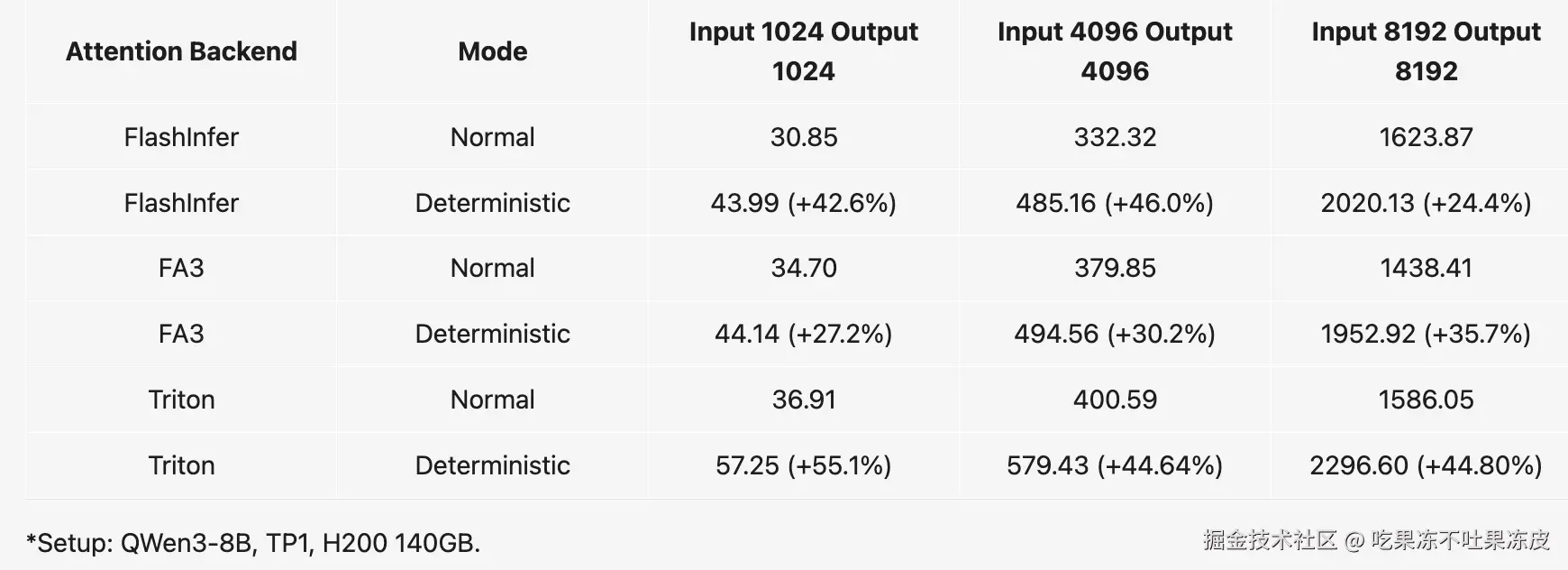
结论：确定性推理大多数情况下推理速度下降在 25% 到 45% 之间，FlashInfer 和 FlashAttention 3 后端的平均速度下降为 34.35%。大部分开销来自未优化的 batch-invariant kernels（矩阵乘法和注意力），其性能改进的空间很大。