基于MATLAB的模糊图像复原

基于MATLAB的模糊图像复原需针对不同退化类型（运动模糊、椒盐噪声）设计针对性算法。

一、运动模糊复原

1. 数学模型与PSF估计

运动模糊图像退化模型为：

g(x,y)=f(x,y)∗h(x,y)+n(x,y)g(x,y)=f(x,y)∗h(x,y)+n(x,y)g(x,y)=f(x,y)∗h(x,y)+n(x,y)

其中h(x,y)h(x,y)h(x,y)为点扩散函数（PSF），形状由运动方向和长度决定。PSF估计是复原关键：

频域分析法：通过傅里叶变换检测频谱中的平行暗线，计算运动角度与长度。
二次变换法：对频谱进行对数变换与Radon变换，精确提取PSF参数。

2. 复原算法实现

(1) 维纳滤波（Wiener Filter）

原理：最小化均方误差，平衡去模糊与噪声抑制。

MATLAB代码：

matlab 复制代码

function restored = wiener_filter(blurred, psf, K)
    blurred_fft = fft2(blurred);
    psf_fft = fft2(psf);
    psf_conj = conj(psf_fft);
    denominator = abs(psf_fft).^2 + K;
    restored_fft = (psf_conj ./ denominator) .* blurred_fft;
    restored = real(ifft2(restored_fft));
end

参数选择：K通过噪声方差与信号功率比估计。

(2) 基于深度学习的盲复原

U-Net架构：编码器提取特征，解码器重建清晰图像，跳跃连接保留细节。

训练流程：

matlab 复制代码

net = unet(256,256,1); % 输入为灰度图像
net = trainNetwork(trainingData, layers, options);
restored = predict(net, blurred);

数据增强：模拟不同运动模糊参数生成训练集。

二、椒盐噪声复原

1. 噪声特性与预处理

椒盐噪声表现为随机黑白像素，需先进行去噪：

中值滤波：对局部区域取中值，保留边缘信息。
matlab 复制代码
```
denoised = medfilt2(noisy_img, [3,3]);
```
自适应TV-L1模型：结合全变差正则化与L1保真度，处理高密度噪声。
matlab 复制代码
```
% 使用Primal-Dual梯度法求解
[u, ~] = imtvdenoise(noisy_img, lambda, 'Method', 'primal-dual');
```

2. 联合去噪与复原

两步法：先中值滤波去噪，再用维纳滤波复原。
联合模型：构建含噪声与模糊的联合正则化模型：

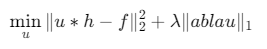
使用交替方向乘子法（ADMM）求解。

三、综合实现流程

输入图像预处理：转换为灰度图像。检测噪声类型（椒盐噪声用中值滤波，高斯噪声用高斯滤波）。
运动模糊参数估计：频域分析或深度学习模型（如CNN）估计PSF。
复原算法选择：低噪声：维纳滤波 + 中值滤波。高噪声：深度学习盲复原（如U-Net）。
后处理优化：边缘增强（Unsharp Mask）。超分辨率重建（ESPCN模型）。

参考代码实现模糊图像的复原，运动模糊复原，椒盐噪声复原 www.youwenfan.com/contentcsi/64279.html

四、MATLAB工具与代码示例

PSNR计算：

matlab 复制代码

function psnr_val = psnr(orig, restored)
    mse = mean((orig(:) - restored(:)).^2);
    if mse == 0
        psnr_val = Inf;
    else
        psnr_val = 10 * log10(255^2 / mse);
    end
end

运动模糊PSF生成：

matlab 复制代码

function psf = motion_psf(size, angle, length)
    psf = zeros(size);
    center = floor(size/2);
    rad = deg2rad(angle);
    for i = 1:length
        x = round(center + i*cos(rad));
        y = round(center + i*sin(rad));
        if x > 0 && x <= size(2) && y > 0 && y <= size(1)
            psf(y,x) = 1/length;
        end
    end
end

五、应用场景与优化建议

实时处理：使用简化U-Net或FFT加速的维纳滤波。
医学影像：结合非局部均值滤波与深度学习，保留细节。
卫星图像：多尺度分解（小波+BM3D）处理混合噪声。