multi-head attention 多头注意力实现细节

论文中关于多头注意力的描述

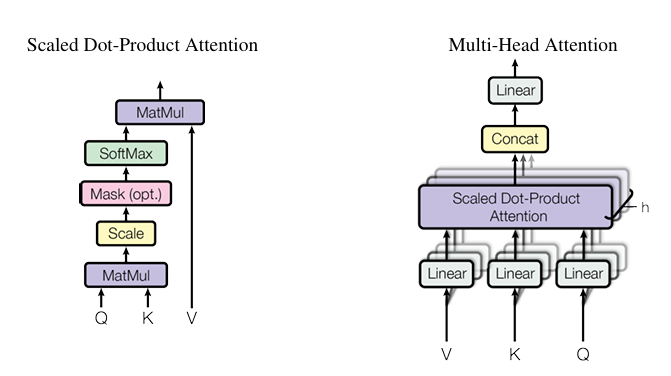
代码实现

python 复制代码

import torch
import torch.nn as nn
import torch.nn.functional as F
import math
 
class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super(MultiHeadAttention, self).__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_k = d_model // num_heads
 
        assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
 
        # Linear projections for Q, K, V
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.W_o = nn.Linear(d_model, d_model)
 
    def scaled_dot_product_attention(self, Q, K, V, mask=None):
        # Q, K, V: (batch_size, num_heads, seq_len, d_k)
        scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_k)
        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))
        attn = F.softmax(scores, dim=-1)
        return torch.matmul(attn, V)
 
    def split_heads(self, x, batch_size):
        # x: (batch_size, seq_len, d_model)
        x = x.view(batch_size, -1, self.num_heads, self.d_k)  # (batch_size, seq_len, num_heads, d_k)
        return x.transpose(1, 2)  # (batch_size, num_heads, seq_len, d_k)
 
    def combine_heads(self, x, batch_size):
        # x: (batch_size, num_heads, seq_len, d_k)
        x = x.transpose(1, 2).contiguous()  # (batch_size, seq_len, num_heads, d_k)
        return x.view(batch_size, -1, self.d_model)  # (batch_size, seq_len, d_model)
 
    def forward(self, Q, K, V, mask=None):
        batch_size = Q.size(0)
 
        Q = self.W_q(Q)  # (batch_size, seq_len, d_model)
        K = self.W_k(K)
        V = self.W_v(V)
 
        Q = self.split_heads(Q, batch_size)  # (batch_size, num_heads, seq_len, d_k)
        K = self.split_heads(K, batch_size)
        V = self.split_heads(V, batch_size)
 
        attn_output = self.scaled_dot_product_attention(Q, K, V, mask)
        output = self.combine_heads(attn_output, batch_size)
 
        return self.W_o(output)  # Final linear projection

会发现其实代码和论文不是完全一样的，论文看起来是每个头有单独的W去乘，但是代码里是所有头共用W再拆分。其实两者是等价的。要注意一下，在multi-head attention中，输入是不被拆分的，它的shape一直是 $L,D_model$ ，拆分的是W，把 $D_model, D_model$ 的矩阵拆分成K个 $D_k, D_model$ 的矩阵。

根据矩阵的乘法定义

复制代码

Y = X W = X [W₁  W₂] = [X W₁   X W₂]

乘之前拆分还是乘之后拆分，是一样的。代码用大矩阵来乘，可以加快计算。