2025-10-16:有向无环图中合法拓扑排序的最大利润。用go语言,给定一个由 n 个节点(编号 0 到 n-1)构成的有向无环图,边集合用二维数组 edges 表示,其中每一项 edges[i] = [u, v] 表示一条从节点 u 指向节点 v 的有向边。每个节点 i 对应一个分值 score[i]。
现在需要按某个合法的拓扑序列依次处理所有节点:在这种序列中,如果存在边 u → v,则 u 必须出现在 v 之前。处理时为序列中的第 k 个节点分配位置编号 k(从 1 开始),并将该节点的分值乘以其位置编号。将所有节点的这些乘积相加得到总收益(或称"利润")。
要求在所有满足有向边约束的拓扑排列中,找出能使总收益最大的排列,并返回该最大收益值。
1 <= n == score.length <= 22。
1 <= score[i] <= 100000。
0 <= edges.length <= n * (n - 1) / 2。
edges[i] == [ui, vi] 表示一条从 ui 到 vi 的有向边。
0 <= ui, vi < n。
ui != vi。
输入图 保证 是一个 DAG。
不存在重复的边。
输入: n = 3, edges = [[0,1],[0,2]], score = [1,6,3]。
输出: 25。
解释:
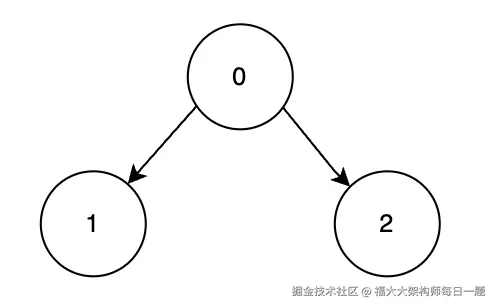
节点 1 和 2 都依赖于节点 0,因此最优的合法顺序是 [0, 2, 1]。
| 节点 | 处理顺序 | 得分 | 乘数 | 利润计算 |
|---|---|---|---|---|
| 0 | 第 1 个 | 1 | 1 | 1 × 1 = 1 |
| 2 | 第 2 个 | 3 | 2 | 3 × 2 = 6 |
| 1 | 第 3 个 | 6 | 3 | 6 × 3 = 18 |
所有合法拓扑排序中可获得的最大总利润是 1 + 6 + 18 = 25。
题目来自力扣3530。
分步骤详细过程
1. 特殊情况处理
- 如果图中没有边(edges为空),说明所有节点之间没有依赖关系,可以任意排列。
- 为了最大化总收益,应该将分值较大的节点放在序列的后面(这样它们会乘以更大的位置编号)。
- 具体做法:将分值数组从小到大排序,然后计算每个分值乘以位置编号(从1开始)的和。
2. 构建先修关系
- 对于每个节点,记录它的所有直接前驱节点(先修课)。
- 使用位掩码表示法:
pre[i]是一个整数,其二进制表示中第j位为1表示节点j是节点i的先修课。 - 例如,如果有边 [0,1] 和 [0,2],那么:
pre[1] = 1 << 0(二进制:001)pre[2] = 1 << 0(二进制:001)
3. 动态规划状态定义
- 使用状态压缩动态规划,状态
s是一个位掩码,表示已经处理过的节点集合。 f[s]表示处理完集合s中的节点后能获得的最大总收益。- 初始化:
f[0] = 0(没有处理任何节点时收益为0),其他状态初始化为-1(表示不可达)。
4. 状态转移过程
- 遍历所有可能的状态
s(从0到2^n - 1)。 - 对于每个有效状态
s(f[s] >= 0):- 计算已处理节点数量:
i = bits.OnesCount(s) - 枚举所有未处理的节点
j:- 检查节点
j的所有先修课是否都已处理:s | pre[j] == s - 如果满足条件,则可以将节点
j作为下一个处理的节点 - 新状态:
newS = s | (1 << j) - 新收益:
f[newS] = max(f[newS], f[s] + score[j] * (i + 1)) - 这里
(i + 1)是节点j在序列中的位置编号
- 检查节点
- 计算已处理节点数量:
5. 最终结果
- 最终状态是处理完所有节点:
s = (1 << n) - 1 - 返回
f[(1 << n) - 1]作为最大收益
示例分析
对于输入:n=3, edges=[[0,1],[0,2]], score=[1,6,3]
处理过程:
- 节点0没有先修课,可以首先处理
- 然后可以处理节点1或节点2(因为它们的先修课0已处理)
- 通过动态规划计算所有可能的拓扑序列:
-
0,1,2\]:收益 = 1×1 + 6×2 + 3×3 = 1+12+9=22
-
- 最终找到最大收益为25
复杂度分析
时间复杂度
- 状态总数:2^n
- 对于每个状态,需要检查最多n个可能的下一节点
- 每个检查操作是O(1)的位运算
- 总时间复杂度:O(n × 2^n)
空间复杂度
- 主要空间开销是DP数组
f,大小为2^n - 先修关系数组
pre,大小为n - 总空间复杂度:O(2^n)
由于n ≤ 22,2^22 ≈ 4百万,这个算法在时间和空间上都是可行的。
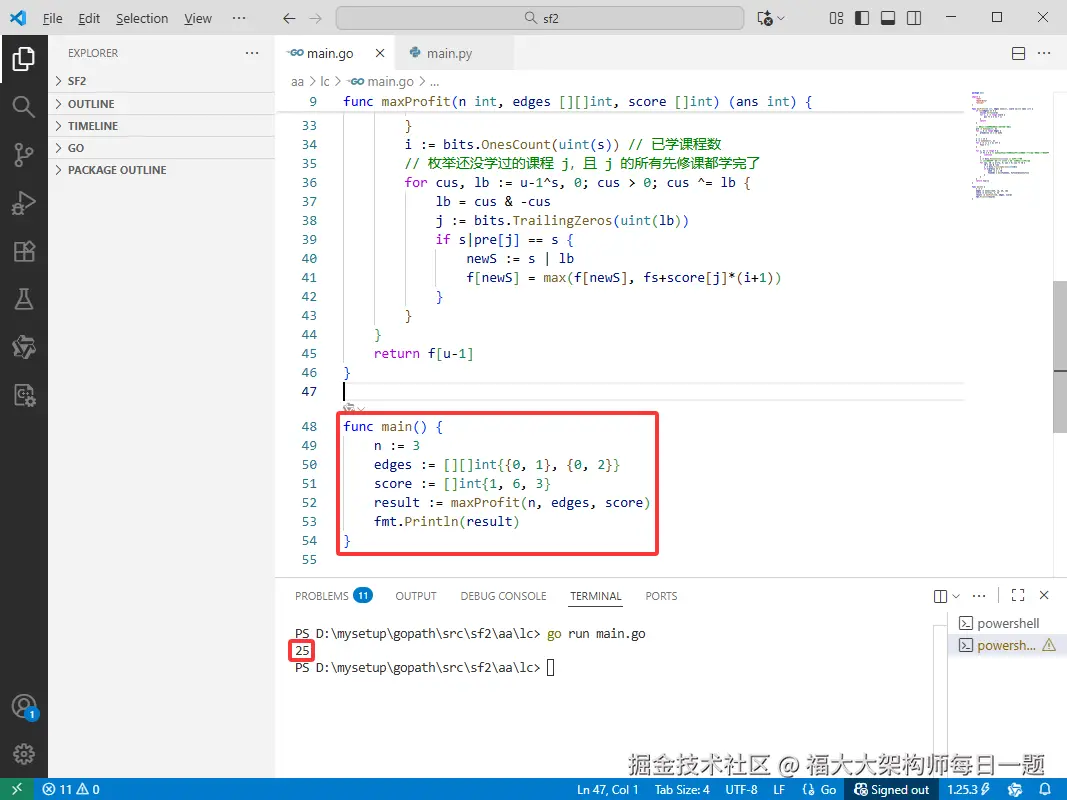
Go完整代码如下:
go
package main
import (
"fmt"
"math/bits"
"slices"
)
func maxProfit(n int, edges [][]int, score []int) (ans int) {
if len(edges) == 0 {
slices.Sort(score)
for i, s := range score {
ans += s * (i + 1)
}
return
}
// 记录每个节点的先修课(直接前驱)
pre := make([]int, n)
for _, e := range edges {
pre[e[1]] |= 1 << e[0]
}
u := 1 << n
f := make([]int, u)
for s := 1; s < u; s++ {
f[s] = -1
}
for s, fs := range f {
if fs < 0 { // 不合法状态,比如已经学完后面的课程,但前面的课程还没学
continue
}
i := bits.OnesCount(uint(s)) // 已学课程数
// 枚举还没学过的课程 j,且 j 的所有先修课都学完了
for cus, lb := u-1^s, 0; cus > 0; cus ^= lb {
lb = cus & -cus
j := bits.TrailingZeros(uint(lb))
if s|pre[j] == s {
newS := s | lb
f[newS] = max(f[newS], fs+score[j]*(i+1))
}
}
}
return f[u-1]
}
func main() {
n := 3
edges := [][]int{{0, 1}, {0, 2}}
score := []int{1, 6, 3}
result := maxProfit(n, edges, score)
fmt.Println(result)
}
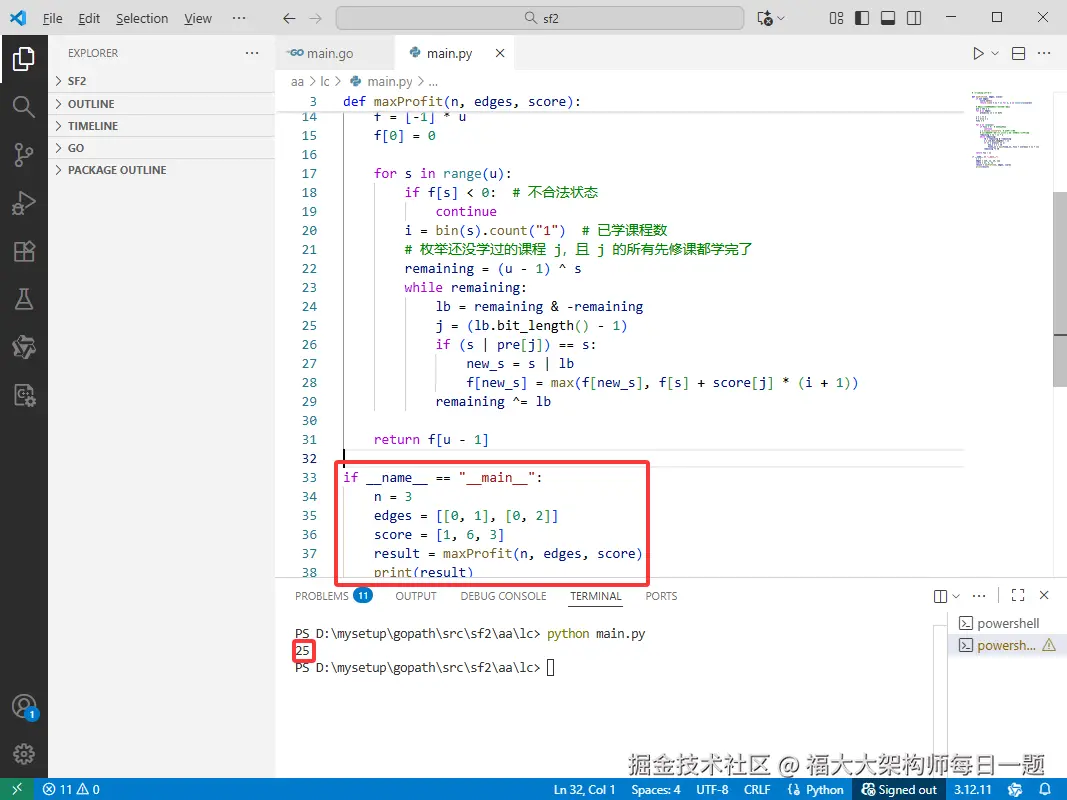
Python完整代码如下:
python
# -*-coding:utf-8-*-
def maxProfit(n, edges, score):
if not edges:
score.sort()
return sum(s * (i + 1) for i, s in enumerate(score))
# 记录每个节点的先修课(直接前驱)
pre = [0] * n
for e in edges:
pre[e[1]] |= 1 << e[0]
u = 1 << n
f = [-1] * u
f[0] = 0
for s in range(u):
if f[s] < 0: # 不合法状态
continue
i = bin(s).count("1") # 已学课程数
# 枚举还没学过的课程 j,且 j 的所有先修课都学完了
remaining = (u - 1) ^ s
while remaining:
lb = remaining & -remaining
j = (lb.bit_length() - 1)
if (s | pre[j]) == s:
new_s = s | lb
f[new_s] = max(f[new_s], f[s] + score[j] * (i + 1))
remaining ^= lb
return f[u - 1]
if __name__ == "__main__":
n = 3
edges = [[0, 1], [0, 2]]
score = [1, 6, 3]
result = maxProfit(n, edges, score)
print(result)