大数据-208 岭回归与Lasso回归：区别、应用与选择指南

TL;DR

场景：解决多重共线性与过拟合问题
结论：岭回归适合高度相关特征，Lasso回归适合特征选择
产出：应用场景与正则化参数λ选择指导

版本矩阵

版本	已验证	说明
Ridge Regression (L2)	已验证	适用于高相关特征的场景，保持所有特征但压缩系数
Lasso Regression (L1)	已验证	适合高维数据和特征选择，能将部分系数压缩为零
Elastic Net	已验证	结合L1和L2正则化的优势，适合综合场景

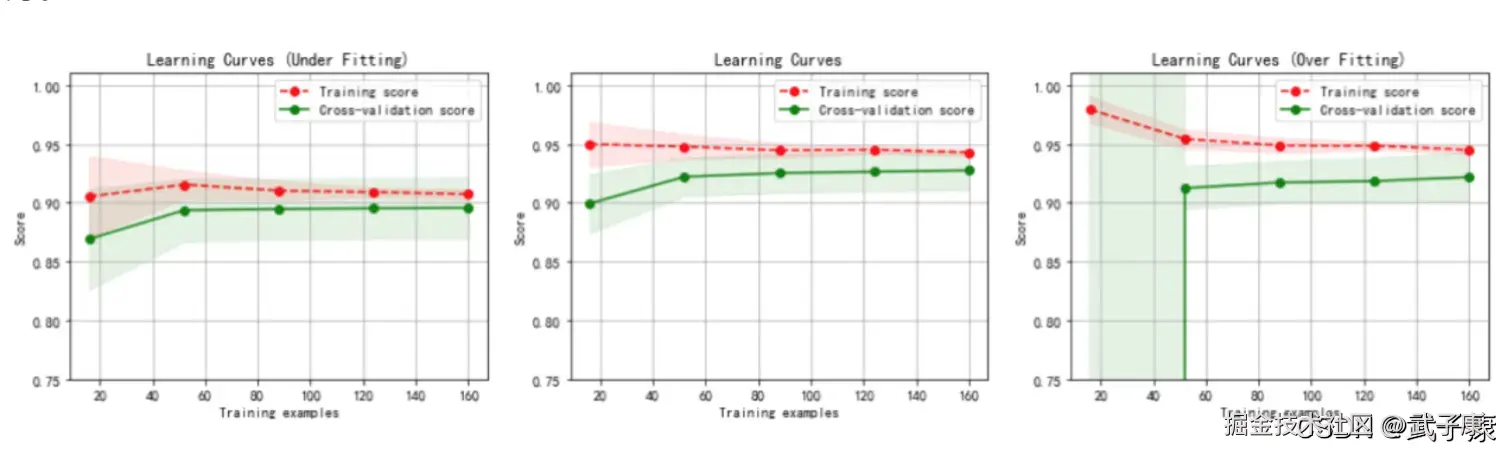
岭回归和Lasso

岭回归（Ridge Regression）和Lasso（Least Absolute Shrinkage and Selection Operator）是两种经典的线性回归正则化方法，专门用于解决机器学习中的过拟合问题和多重共线性问题。这两种方法的核心思想都是在普通最小二乘法（OLS）的基础上，通过引入不同的正则化项来约束模型参数。

岭回归（L2正则化）：

添加L2范数惩罚项：在损失函数中加入回归系数平方和的惩罚项（λ∑β²）
特点：所有特征都会被保留，但系数会被压缩
适用场景：当特征之间存在高度相关性时（如基因表达数据）
数学表达式：min(∑(y_i - ŷ_i)² + λ∑β_j²)

Lasso回归（L1正则化）：

添加L1范数惩罚项：在损失函数中加入回归系数绝对值的惩罚项（λ∑|β|）
特点：可以实现特征选择，部分系数会被压缩为零
适用场景：当特征维度很高且需要特征选择时（如文本分类）
数学表达式：min(∑(y_i - ŷ_i)² + λ∑|β_j|)

实际应用中的典型场景：

房价预测：当房屋特征（面积、房间数、地理位置等）存在多重共线性时
基因数据分析：处理成千上万个基因表达数据时
金融风控：从数百个财务指标中筛选关键风险因子

这两种方法的区别主要体现在：

岭回归会使所有系数都缩小但不为零，适合保留所有特征的情况
Lasso会使得部分系数变为零，实现特征选择
弹性网络（Elastic Net）结合了两者的优点，同时使用L1和L2正则化

选择建议：

当预测性能比可解释性更重要时，选择岭回归
当需要特征选择和模型可解释性时，选择Lasso
在实际应用中，通常需要通过交叉验证来确定最佳的正则化参数λ

岭回归的原理

岭回归是在普通线性回归的基础上加入了L2正则化项，使得模型更鲁棒。具体来说，岭回归的损失函数是普通最小二乘法的损失函数与一个L2正则化项之和。该正则化项是回归系数的平方和可以在极小化损失的同时，约束回归系数的大小，避免其过大从而导致模型过拟合。

Lasso回归的原理

Lasso回归（Least Absolute Shrinkage and Selection Operator）与岭回归（Ridge Regression）都是线性回归的正则化变体，但它们在正则化方式上存在显著差异：

正则化项类型：

Lasso回归采用L1正则化，即对系数绝对值之和进行惩罚：λΣ|β_j|
岭回归采用L2正则化，即对系数平方和进行惩罚：λΣβ_j²

特征选择能力：

Lasso的L1惩罚会导致某些系数完全收缩为零，实现自动特征选择
岭回归的L2惩罚会使所有系数都趋向于变小，但不会完全归零

数学特性差异：

Lasso的解在几何上对应菱形约束区域顶点
岭回归的解对应圆形约束区域

适用场景对比：

当特征数量远大于样本量时（p>>n），Lasso通常表现更好
当存在高度相关特征时，岭回归往往更稳定

实际应用示例：在基因表达数据分析中（通常有数万个基因特征），Lasso能有效识别出少数关键基因；而在经济学时间序列预测中（特征间高度相关），岭回归能提供更稳健的预测。
参数选择：两种方法都需要通过交叉验证确定最优正则化参数λ，但Lasso的λ通常需要更精细的网格搜索来捕捉特征选择的关键阈值。

注意：在实践中，Elastic Net（结合L1和L2正则化）常被用作折中方案，兼具两种方法的优势。

解决方式

解决共线性的问题的方法主要有以下三种：

其一是在建模之前对各特征进行相关性检验，若存在多重共线性，则可以考虑进一步对数据集进行 SVD 分解或 PCA 主成分分析，在 SVD 或 PCA 执行的过程中会对数据集进行正交交换，最终所得数据集各列将不存在任务任何相关性。当然此举会对数据集的结构进行改变，且各列特征变得不可解释。
其二则是采用逐步回归的方法，以此选取对因变量解释力度最强的自变量，同时对于存在相关性的自变量加上一个惩罚因子，削弱其对因变量的解释力度，当然该方法不能完全避免多重共线性的存在，但能够绕过最小二乘法对共线性较为敏感的缺陷，构建线性回归模型。
其三则是在原有算法基础上进行修改，放弃对线性方程参数无偏估计的苛刻条件，使其能够容忍特征列存在多重共线性的情况，并且能够顺利建模，且尽可能的保证 SSE 取得最小值。

通常来说，能够利用一个算法解决的问题尽量不用多个算的组合来解决，因此此处我们主要考虑后两个方案，其中逐步回归我们将放在线性回归的最后一部分进行讲解，而第三个解决方案，则是我们接下来需要详细讨论的岭回归算法和 Lasso 算法。

岭回归和Lasso回归在加入正则化项的方式上有所不同，从而影响模型的选择和应用。岭回归更适合用于避免系数过大而导致的过拟合，而Lasso在特征选择方面更有优势，因此通常在高维数据中表现更佳。在实际应用中，可以通过交叉验证来选择最适合的正则化参数并在岭回归和Lasso之间做出选择，或者结合两者（Elastic Net）以获得更好的模型效果。

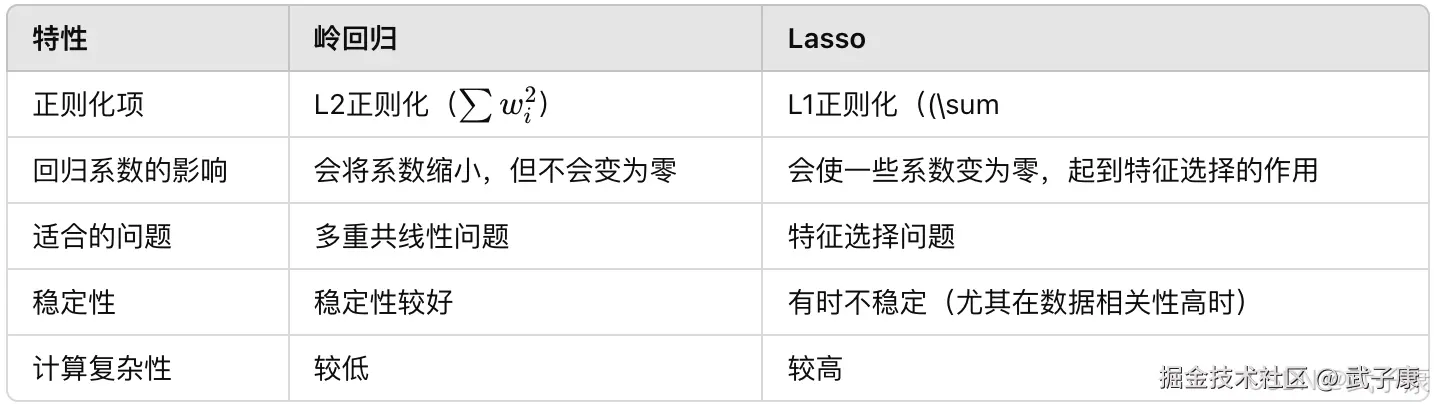
岭回归

基本原理

岭回归算法实际上是针对线性回归算法局限性的一个改进类算法，优化目的是解决系数矩阵XTX不可逆的问题，客观上同时也起到了克服数据集存在多重共线性的情况，而岭回归的做法也非常简单，就是在原方程系数计算公式中添加了一个扰动项，原先无法求广义逆的情况变成了求出其广义逆，使得问题稳定并得以求解。岭回归在多元线性回归的损失函数上加上了正则项，表达为系数 w 的 L2 范式（即系数 w 的平方项）乘以正则化系数 λ，岭回归的损失函数的完整表达式写作：

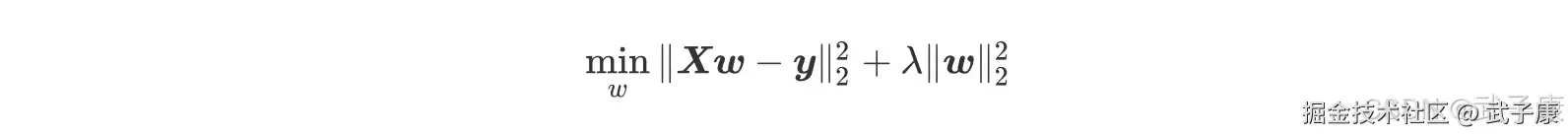我们仍然可以使用最小二乘法求解，可得：此举看似简单，实则非常精妙，用一个满秩的对角矩阵和原系数矩阵计算进行相加的，实际上起到了两个作用，其一是使得最终运算结果（XTX + λI）满秩，即降低了原数据集特征列的共线性影响，其二也相当于对所有的特征列的因变量解释程度进行了惩罚，且λ越大惩罚作用越强。

现在，只要（XTX + λI）存在逆矩阵，我们就可以求解。一个矩阵存在逆矩阵的充分必要条件是这个矩阵的行列式不为0。假设原本的特征矩阵中存在共线性，则我们的方阵 XTX 就会不满秩（存在完全为零的行）。

此时方阵 XTX 就是没有逆的，最小二乘法就无法使用，加上了λI 之后，我们的矩阵就大不一样了：

最后得到的行列式还是一个梯形行列式，然而它已经不存在全 0 行或者全 0 列了，除非：

λ 等于 0
原本的矩阵 XTX中存在对焦线上元素为 -λ，其他元素都为0 的行或者列

否则矩阵 XTX+λI 永远都是满秩，在 sklearn 中，λ的值我们可以自由的控制，因此我们可以让它不为 0，比避免第一种情况。而第二种情况，如果我们发现某个λ的取值下模型无法求解，那我们只需要更换一个λ的取值就好了，也可以顺利避免。也就是说，矩阵的逆永远存在，有这个保障，我们的 w 就可以写作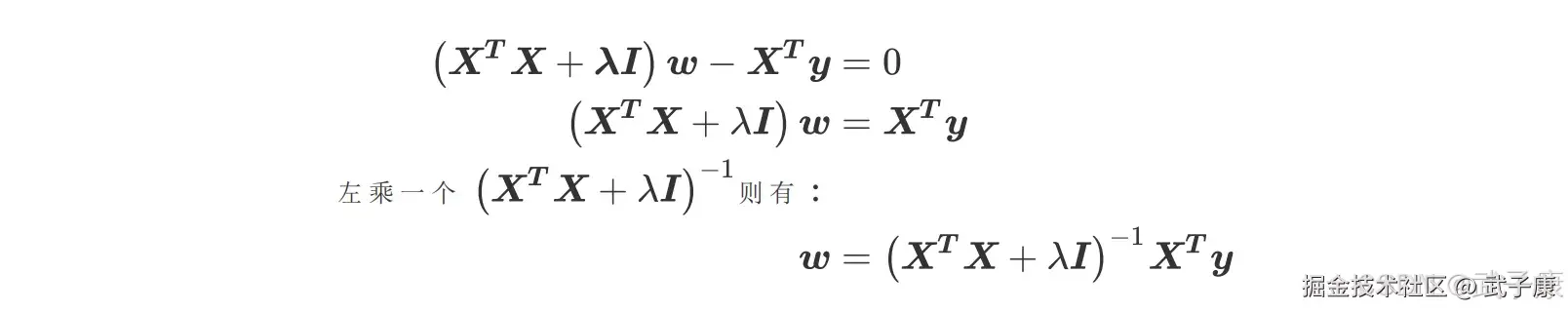：如此，正则化系数λ就避免了精确相关关系带来的影响，至少最小二乘法在λ存在的情况下是一定可以使用。对于存在高度相关关系的矩阵，我们也可以通过调大λ，来让 XTX+λI 矩阵的行列式变大，从而让逆矩阵变小，以此控制参数向量 w 的偏移。当λ越大，模型越不容易受到共线性的影响。

Lasso

基本原理

在岭回归中，对自变量系数进行平方和处理也被称做 L2 正则化，由于此原因，岭回归中自变量系数虽然会很快衰减，但很难归为零，且窜在共线性的时候衰减过程也并非严格递减，这就是为何岭回归能够建模、判断共线性，但很难进行变量筛选的原因。为了弥补岭回归在这方面的不足，Tibshirani（1996）提出了 Lasso（The Least Absolute Shrinkage and Selectiontorperator）算法，将岭回归的损失函数中的自变量系数 L2 正则化修改为 L1 正则化，即 Lasso 回归损失函数为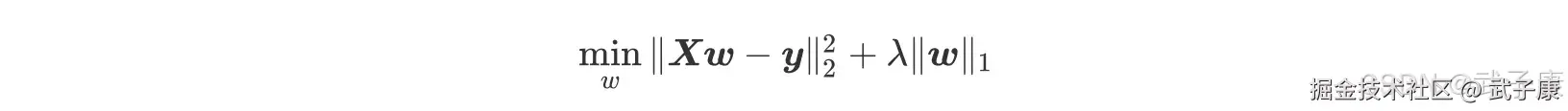：我们来看看 Lasso 的计算过程，当我们使用最小二乘法来求解 Lasso 中参数，我们依然对损失函数进行求导：现在问题又回到了要求 XTX 的逆必须存在，在岭回归中，我们通过正则化系数λ能够向方阵 XTX 加上一个单位矩阵，以此来防止方阵 XTX 的行列式为 0，而现在 L1 范式所带的正则项λ在求导之后并不带有w 这个项，因此它无法对 XTX 造成任何影响。也就是说，Lasso 无法解决特征之间精确相关的问题，当我们使用最小二乘法求解线性回归时，如果线性回归无解或者报除零的错误，换 Lasso 不能解决任何问题。不过，在现实中我们其实会比较少遇到精确相关的多重共线性问题，大部分多重共线性问题应该时高度相关，而如果我们假设方阵 XTX 的逆是一定存在的，那我们可以有：

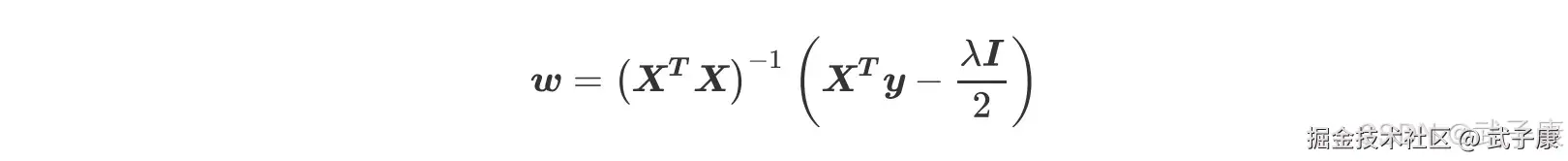通过增大λ，我们可以为 w 的计算增加一个负项，从而限制参数估计中 w 的大小，而防止多重共线性引起的参数 w 被估计过大导致模型失准的问题，Lasso 不是从根本上解决多重共线性问题，是限制多重共线性带来的影响。

错误速查

症状	根因	定位修复方法
无法求解模型	特征矩阵共线性	特征矩阵XTX不可逆，通过岭回归或增大λ值
过拟合	模型复杂度过高	特征过多且无有效选择，使用Lasso进行特征选择
特征选择不足	岭回归无法将特征压缩为零	需要自动化特征选择，使用Lasso或Elastic Net

其他系列

🚀 AI篇持续更新中（长期更新）

AI炼丹日志-29 - 字节跳动 DeerFlow 深度研究框斜体样式架私有部署测试上手架构研究 ，持续打造实用AI工具指南！ AI研究-132 Java 生态前沿 2025：Spring、Quarkus、GraalVM、CRaC 与云原生落地

💻 Java篇持续更新中（长期更新）

Java-218 RocketMQ Java API 实战：同步/异步 Producer 与 Pull/Push Consumer MyBatis 已完结，Spring 已完结，Nginx已完结，Tomcat已完结，分布式服务已完结，Dubbo已完结，MySQL已完结，MongoDB已完结，Neo4j已完结，FastDFS 已完结，OSS已完结，GuavaCache已完结，EVCache已完结，RabbitMQ已完结，RocketMQ正在更新... 深入浅出助你打牢基础！

📊 大数据板块已完成多项干货更新（300篇）：

包括 Hadoop、Hive、Kafka、Flink、ClickHouse、Elasticsearch 等二十余项核心组件，覆盖离线+实时数仓全栈！ 大数据-278 Spark MLib - 基础介绍机器学习算法梯度提升树 GBDT案例详解