代数类型其实并不可怕
你可能之前听说过"代数类型(algebraic types)"这个术语,乍一听似乎是一个高级概念,只有编程语言博士才能理解。恰恰相反,代数类型是一个非常简单且实用的编程概念。任何了解基础代数的人都能理解什么是代数类型。
在本文中,我旨在为程序员解释代数类型。我有意避免使用普通程序员可能不了解的术语。我希望读完本文后,您能够了解代数类型是什么,并能够在实际编程中使用它,并能识别它出现的位置。
把类型(Type) 看作一个 集合
类型究竟是什么?例如,当我们写 int 时,它意味着什么?一种有用的思考方式是将类型视为集合。从这个角度来看,每种类型都被视为与该类型兼容的一组可能值。例如, bool 是一种只有 true 和 false 值的类型。在 OCaml 中, bool 的定义如下:
ocaml
type bool = true | false在左侧,我们定义类型 bool 。右侧提供可能的值,以 | 分隔。
对于整数,这个值可以是 0 、 1 或任何其他整数值。将整数直接定义为常规类型会稍微困难一些,因为在这种情况下,整数可以取无限多个值。不可能写出所有这些值。但假设可以,我们可以这样写:
ocaml
type int = ... | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ...在实践中,整数类型通常被限制在某个有限的范围内(但仍然太大),但这与我们这里讨论的内容无关。从这个角度来看,字符串与整数非常相似。
那么 void 类型呢?它接受哪些值?在某些语言中,这一点并不明显,但我们可以认为 void 只有一个可能值。例如,在 OCaml 中, unit(unit 意思是"单位") 对应于 void 。它的定义如下:
ocaml
type unit = ()在 C、C++ 或 Java 中, void 与其他类型的处理方式不同 ,这导致它在某些情况下难以使用。如果我们将其视为其他类型,则无需为 void 设立例外。这简化了类型系统以及编程语言的实现。理解代数类型之后,我会举一些例子来说明这一点。
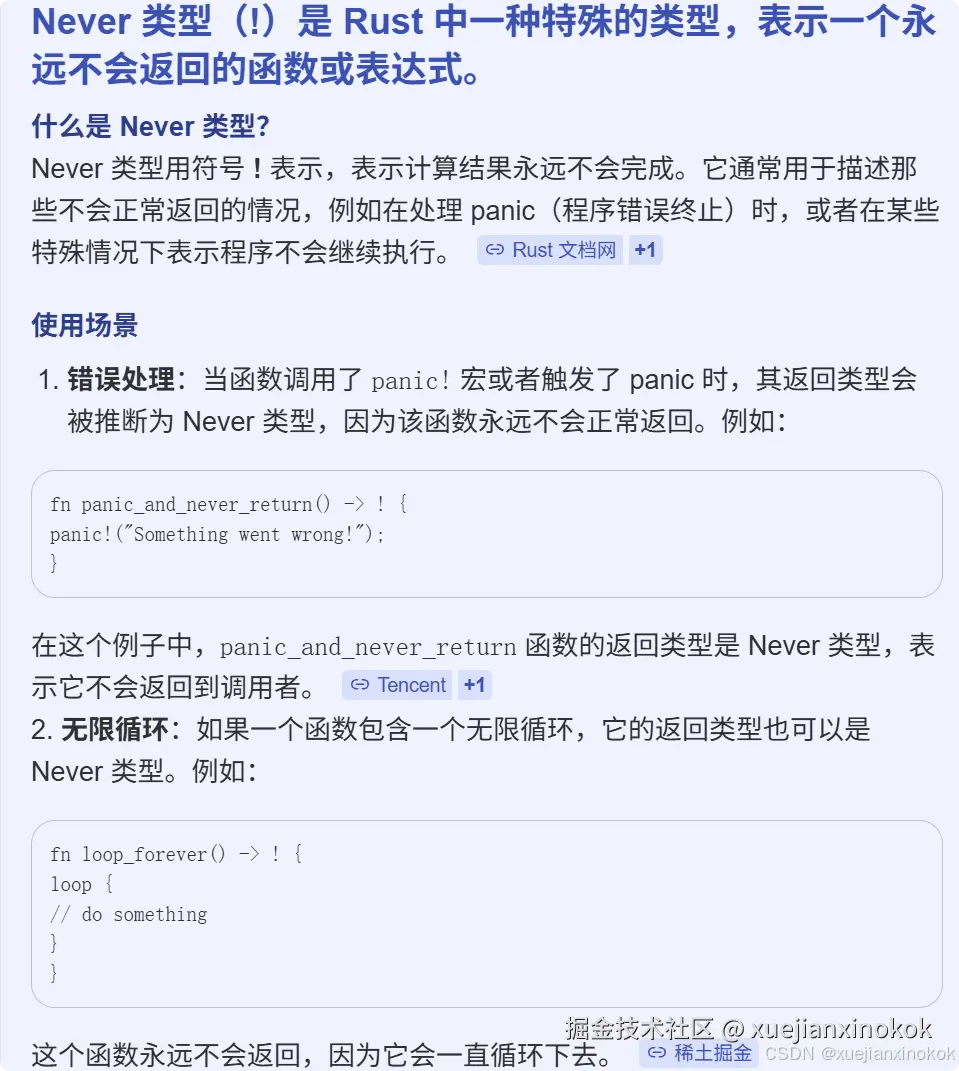
另一个有趣的例子是 非终止(non-termination)。永不返回的 while 循环是什么类型?好吧,从集合的角度来看,如果表达式不返回任何值,那么它的类型可能就是一个没有可能值的类型?注意,这种类型与 void 不同 ,因为 void 可以接受一个值,而这种类型不接受任何值。有时这种类型被称为 never ,因为它永远不可能有这种类型的值。我们也可以简单地将此类型定义为:
ocaml
type never由于此类型没有值,因此不可能存在此类型的值。因此,我们可以将其用作 不终止(doesn't terminate)的表达式或函数的类型。因为,如果它终止(terminate)并返回一个值,我们将收到类型错误,指示该值不符合指定的类型。
代数类型只是小学代数
使用这种将 类型 视为 值集合 的视图,理解代数类型就变得非常容易了。事实上,它实际上是基于你在小学学过的代数知识!
什么是数字代数 ?它是加法、乘法、减法和除法。代数类型就是这样,它本质上是对类型进行代数运算 。所以本质上它是对类型的加法和乘法。
Product Types 乘法类型(积类型)
让我们从更熟悉的开始。如果你有两个类型 T1 和 T2 ,那么它还能包含哪些其他类型呢?好吧,你可以有一个包含这两种类型的值,一个来自 T1 ,一个来自 T2 。类似于主流语言中 struct 或 class 工作方式。我们可以在 Java 中将其表达为:
java
class Pair {
T1 first;
T2 second;
}在代数类型术语中,这称为乘法类型 。原因很简单,当您组合两种类型时,结果类型包含其部分是来自相应类型的值的每个值。如果第一种类型有 N 个值,第二种类型有 M 值。我们假设两者都是枚举类型,其中 N 有 2 个变量, M 有 3 个变量。如果我们从 N 和 M 创建一个对类型,我们可以有 6 不同的值。因为我们可以从 N 中选择 2 个,从 M 中选择 3 个,结果为 2 * 3 = 6 因此,一般情况下的对类型有 N * M 个值,因此称为乘法。
每种主流语言都支持这个概念,因为这是一个非常常见的用例,我相信这不需要任何说服。但是,大多数语言不支持将两种类型组合 为一等公民构造(比如:元组类型),因此必须为每种组合明确定义一种新类型 。实际上,这种缺乏会导致更糟糕的 API 设计,例如使用指针/引用 [1] 返回多个值或 Go 的多个返回值 [2] 的模式,因为要返回多个参数,必须创建自定义类型 。没有乘法类型会迫使您使用更专业的构造 来规避它,从而产生意外的复杂性。支持乘法类型作为一等公民(参见 Rust 和 OCaml 作为示例)使语言更简单、更统一,从而减少用户的认知负担 [3] 。
Sum Types 加法类型(和类型)
如果你从未使用过函数式语言,那么这部分可能不太明显。但这确实是编程中一个常见的用例,你可能之前遇到过使用 sum 类型的问题。
加法类型是由两种其他类型组成的类型,其值可以来自第一种类型或第二种类型 。例如,如果你想表示一个易错的算术运算,如果成功 则结果为 int ,如果失败 则结果为包含错误消息的 string ,则该结果的类型为 int 或 string 。
sum(加法,和) 这个名字的由来是,类似于product(乘法,积),如果你从类型 N 和 M 创建一个 sum 类型,你将得到一个包含 N + M 个不同可能值的类型。因为第一个类型可以有 N 选项,第二个类型可以有 M 选项。它类似于逻辑或 ,因为 sum 类型的值实际上来自第一个类型或第二个类型。
sum类型在现实生活中很常见。可以为 null 值就是 sum类型,在编程语言中通常称为 Option 或 Maybe 。在 OCaml 中,它的定义如下:
ocaml
type a option = Some of a | Nonea 表示泛型类型,如果你熟悉 Java,它相当于 Option<A> 。首先构造 Some 表示存在值的情况,而 None 对应于命令式语言中的 null 。这不仅仅是一个例子, option 类型在用 OCaml 和其他函数式语言编写的程序中非常常用。在类型级别使用 null 可以避免许多运行时错误并减少代码冗余(你不必到处都写 null 检查)。
另一个例子是 为错误建模。在 Go 中,当一个函数可以返回错误时,惯用的做法是将其作为第二个值返回。按照惯例,第一个值或第二个值要么为 nil (Go 的 null 值)。 go 如何返回错误 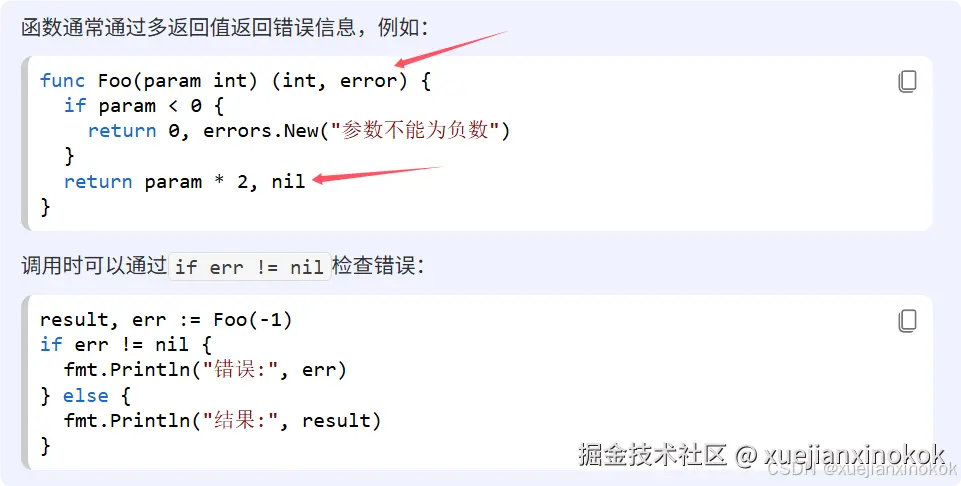
然而,这种约定是隐式的,并没有强制执行。因此,当你返回两个值时,会有 4 种情况,但实际上你假设实际只会发生两种情况。如果两个值都不是 null 或 null ,那就违反了假设。我们可以用一张表来总结:
| Value 1 | Value 2 | Assumed |
|---|---|---|
present |
null |
yes |
null |
null |
yes |
present |
present |
no |
null |
null |
no |
问题在于,类型检查器永远不会验证这个不变量,因此用户必须注意这个约定,这会给用户带来不必要的认知负担。例如, io.Reader 接口可能会返回 EOF 错误 ,同时还会返回一些数据 。这并非一般 Go 程序员所期望的情况,因为他们期望 err 或 val 中的一个 nil 。即使文档中已经提到过,这种差异仍然会在实际生活中导致 bug 。
另一个缺点是,除非文档中明确说明或程序员阅读了完整代码,否则他们无法知道 product 实际上是打算建模一个 sum 类型。相比于签名中的 sum 类型,这两种情况都会增加认知负担。此外,缺少 sum 类型通常会导致实际应用中出现 bug,例如任何需要人工验证的情况,比如这个 bug 。
相反,我们可以简单地使用 sum 类型来表示成功和错误, 前者 返回结果值,后者返回错误信息。在 OCaml 中,有一个 result 类型专门用于此目的:
ocaml
type (a, b) result = Ok of a | Error of b当我们有一个类型为 error 的值时,类型检查器会强制只发生两个期望的条件,并且不希望的条件不可能在代码中表示,从而使代码更简单且不易出错。
在实践中使用代数类型
为了演示代数类型的实际优势,我们来编写一个算术表达式的解释器。我们只包含整数和算术运算符。我们不会讨论如何解析算术表达式,因为它与本文主题无关。
表达式的类型自然地由定义得出:
ocaml
type expr =
| Number of int
| Add of { left : expr; right: expr }
| Sub of { left : expr; right: expr }
| Mul of { left : expr; right: expr }
| Div of { left : expr; right: expr }第一种情况表示操作数为整数。以下情况对应于每个算术运算符。例如, 2 + (3 * 2) 对应于:
ocaml
let e = Add {
left = Number 2;
right = Mul {
left = Number 3;
right = Number 2;
}
}为了 评估表达式,我们可以使用模式匹配编写一个简单的评估器:
ocaml
let rec eval (e : expr) : int =
match e with
| Number n -> n
| Add { left; right } ->
(eval left) + (eval right)
| Sub { left; right } ->
(eval left) - (eval right)
| Mul { left; right } ->
(eval left) * (eval right)
| Div { left; right } ->
(eval left) / (eval right)如果您不熟悉模式匹配,它可以帮助我们确定值具有哪种变体。可能的变体来自其类型。在本例中,根据 expr 的定义,我们知道它要么是 Number ,要么是四种运算之一。对于数字类型,我们可以直接返回它。在其他情况下, left right 的类型都是 expr ,因此首先我们必须递归地计算这些子项以获得它们的 int 值。然后,我们可以使用适当的运算符来计算当前表达式的值。
如果没有代数类型,怎么实现呢?带有继承的抽象方法可以用来模拟求和类型 。所以我们可以有一个抽象基类 Expr 然后针对每种情况对其进行扩展:
java
abstract class Expr { abstract int eval(); }
class Number extends Expr {
int value;
int eval() { return value; }
}
class Plus extends Expr {
Expr left, right;
int eval() { return left.eval() + right.eval(); }
}
// Rest is omitted基类 Expr 有一个方法 eval ,它返回表达式的求值结果。每个子类都实现了它,并递归调用子表达式的 eval 方法。在这种情况下,数据结构没有明确的定义,但它与行为混合在一起。
如果我们想以不同的方式解释表达式怎么办?假设我们只想将其转换为书面形式。对于基于继承的解决方案,我们必须向类添加一个新的基方法,然后在子类中实现它,例如 eval 。使用代数类型,我们可以编写另一个执行模式匹配的函数。例如:
ocaml
let rec expr_to_string (e : expr) : string =
match e with
| Number n -> string_of_int n
| Add { left; right } ->
"(" ^ (expr_to_string left) ^ "+" ^ (expr_to_string right) ^ ")"
| Sub { left; right } ->
"(" ^ (expr_to_string left) ^ "-" ^ (expr_to_string right) ^ ")"
| Mul { left; right } ->
"(" ^ (expr_to_string left) ^ "*" ^ (expr_to_string right) ^ ")"
| Div { left; right } ->
"(" ^ (expr_to_string left) ^ "/" ^ (expr_to_string right) ^ ")"我不知道你是怎么想的,但我觉得后一种方法更好。因为在继承方法中,相关行为彼此之间距离很远。当有人想理解字符串转换的工作原理时,他们需要遍历每个类。而使用模式匹配,相关逻辑则更接近。另一个问题是,操作 在类中以方法的形式实现,因此它们可以完全访问对象的内部结构。然而,这些操作应该只访问对象的公共接口。
抽象方法并非唯一的选择。访问者模式 [4] 专门用于建模具有对象层次结构的和类型 [5] 。使用访问者模式,我们可以得到以下实现:
java
abstract class Expr {
abstract <R> R accept(Visitor<R> visitor);
}
class Number extends Expr {
int value;
<R> R accept(Visitor<R> visitor) { return visitor.visit(this); }
}
class Plus extends Expr {
Expr left, right;
<R> R accept(Visitor<R> visitor) { return visitor.visit(this); }
}
class Mul extends Expr {
Expr left, right;
<R> R accept(Visitor<R> visitor) { return visitor.visit(this); }
}
class Sub extends Expr {
Expr left, right;
<R> R accept(Visitor<R> visitor) { return visitor.visit(this); }
}
class Div extends Expr {
Expr left, right;
<R> R accept(Visitor<R> visitor) { return visitor.visit(this); }
}
interface Visitor<R> {
R visit(Number number);
R visit(Plus plus);
R visit(Mul mul);
R visit(Sub sub);
R visit(Div div);
}
class EvalVisitor implements Visitor<Integer> {
public Integer visit(Number number) { return number.value; }
public Integer visit(Plus plus) { return plus.left.accept(this) + plus.right.accept(this); }
public Integer visit(Mul mul) { return mul.left.accept(this) * mul.right.accept(this); }
public Integer visit(Sub sub) { return sub.left.accept(this) - sub.right.accept(this); }
public Integer visit(Div div) { return div.left.accept(this) / div.right.accept(this); }
}与简单的继承方法相比,它解决了必须向基类添加新方法的问题。此外,相关逻辑位于一个地方,在本例中是访问者模式的实现。然而,它比模式匹配冗长得多,也更难理解 。与模式匹配相比,它具有更大的偶然复杂性 [6] 。本质上,访问者模式是穷人版的模式匹配 。正如 Mark Seeman 所说 [5] :
这并不是说这两种表示在可读性或可维护性上是相同的。F# 和 Haskell 的和类型是声明式类型,通常只需几行代码。而访问者类型则是一个小型的对象层次结构;它以一种更冗长的方式表达了"类型由互斥和异构情况定义"这一概念。我知道我更喜欢哪种替代方案,但如果我被困在面向对象的代码库中,很高兴知道仍然可以使用代数数据类型来建模领域。
结论
简而言之,对于大多数编程任务,你需要两种基本方法来组合类型 : product和sum。通过这两种方法,你可以创建任意结构来模拟现实世界的数据。大多数语言都有方法来表达这两种结构,尽管有些表达方式比较繁琐,例如使用继承来模拟和类型。使用基本概念,你可以用更简单的方式建模,而不会引入不必要的复杂性。
Java中增加了 record 实现product 类型 和 Sealed class 实现 sum类型 和 增强的switch 来进行模式匹配.
参考文章
原文:# Algebraic Types are not Scary, Actually