红黑树 B树 B+树 WTF!M3?
- 前言
- 哈夫曼编码
- 散列表
- 红黑树
-
-
- [AVL树VS 红黑树](#AVL树VS 红黑树)
- 插入(重要)
-
- uncle结点为红的情况(可能需要调整两次)
-
- [step 1](#step 1)
- [step 2](#step 2)
- uncle结点为黑色的情况
-
- [step 1](#step 1)
- 构建一颗红黑树的完整过程
-
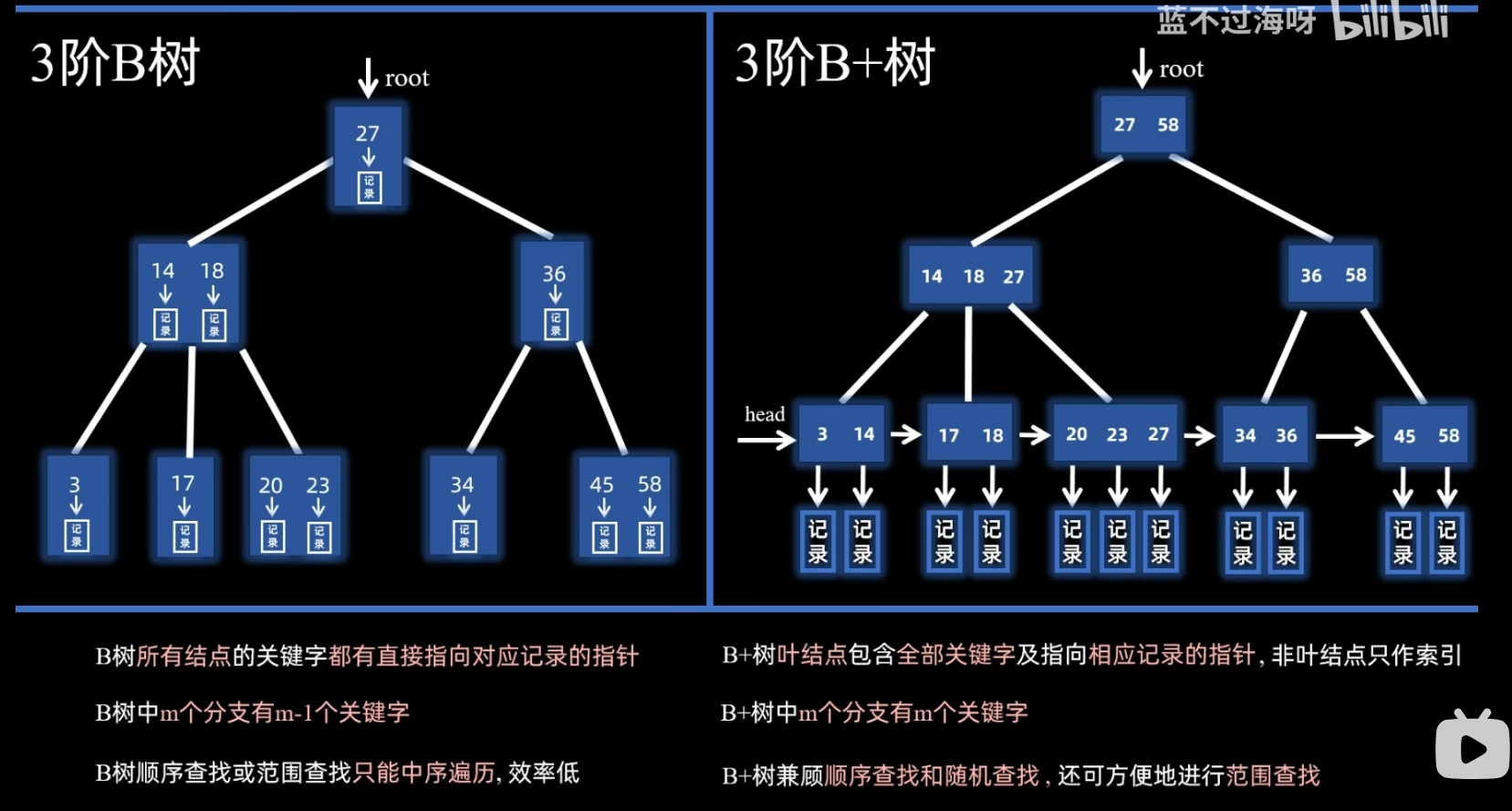
- B树
- B+树
- [B树 VS B+树](#B树 VS B+树)
前言
在学习这篇文章之前建议先学习二叉搜索树和平衡二叉树 可以参考我的文章彻底弄懂各种二叉树
下文所有PPT和文字都是基于B站蓝不过海呀的视频所写内容非常优质 十分建议初学者观看
一切数据结构一旦以动画的形式呈现就变得不再晦涩难懂了 respect!
哈夫曼编码
引入
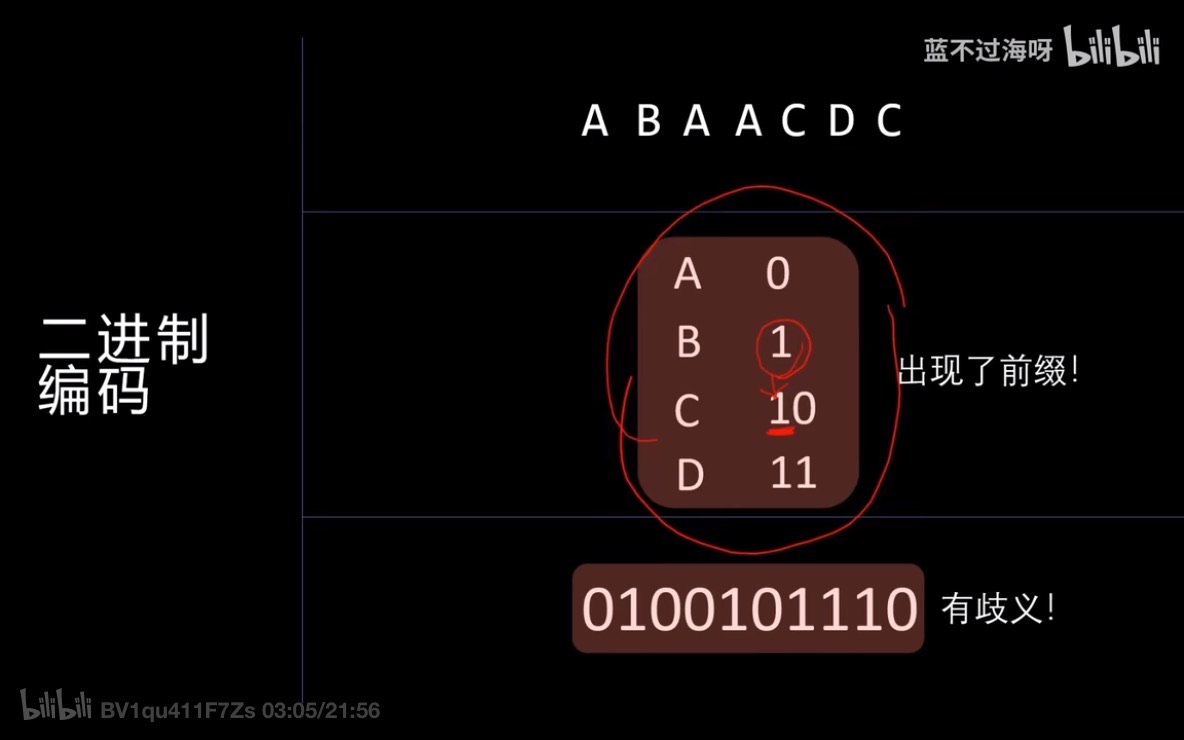
- 假如我们想用一串二进制数字来表示一串字符 那么我们可以用二进制代表每个字母 例如下图当中 A=0 B=1 C=10 D=11
- 出现歧义的原因是因为我们在二进制编码当中出现了相同前缀 导致我们在译码的时候会发现结果是不唯一的,
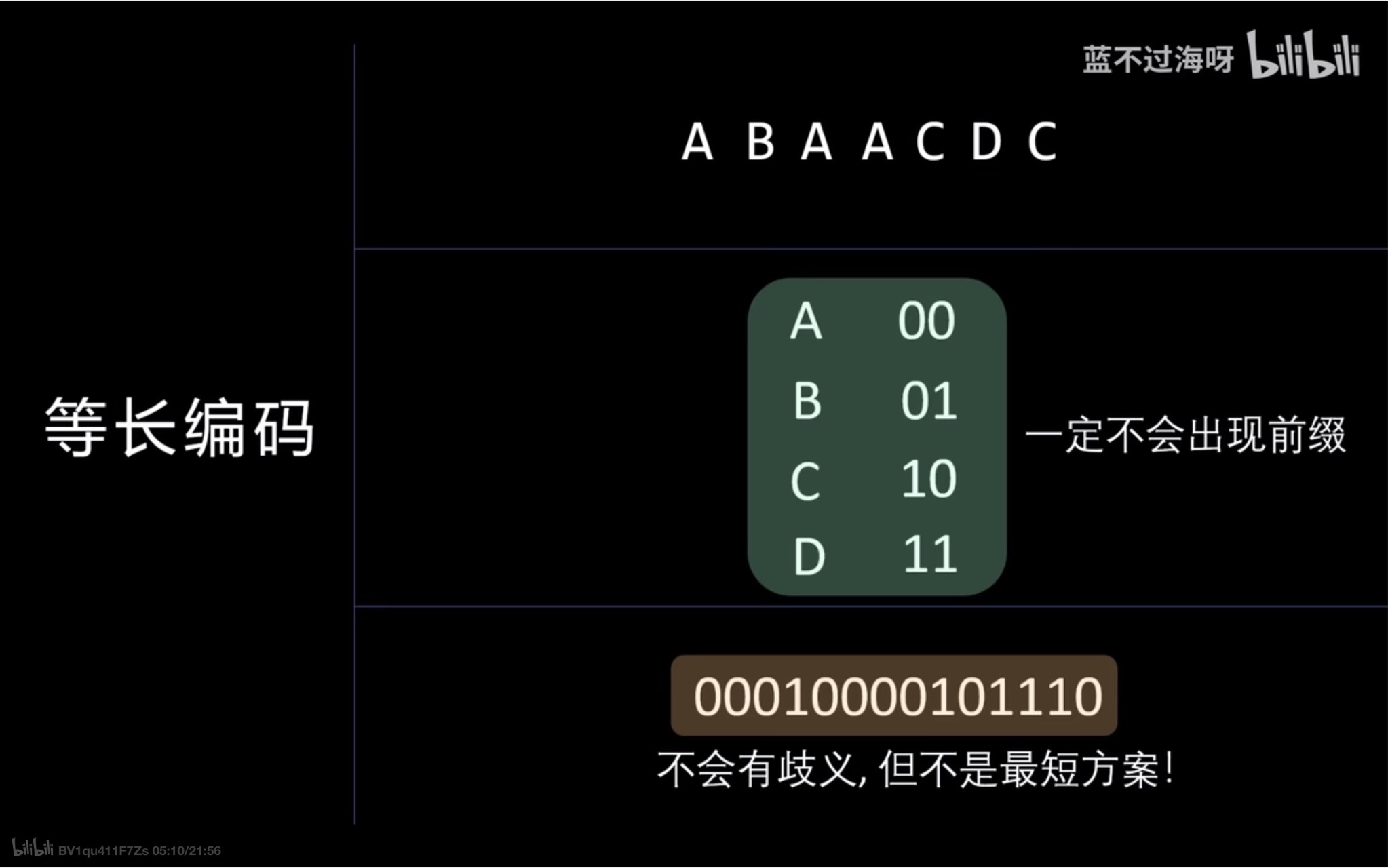
小优化
进阶
- 统计在一串字符当中每个字符出现的次数
- 采用合并操作建立哈夫曼树(每次选择最小的两个将他们合二为一)
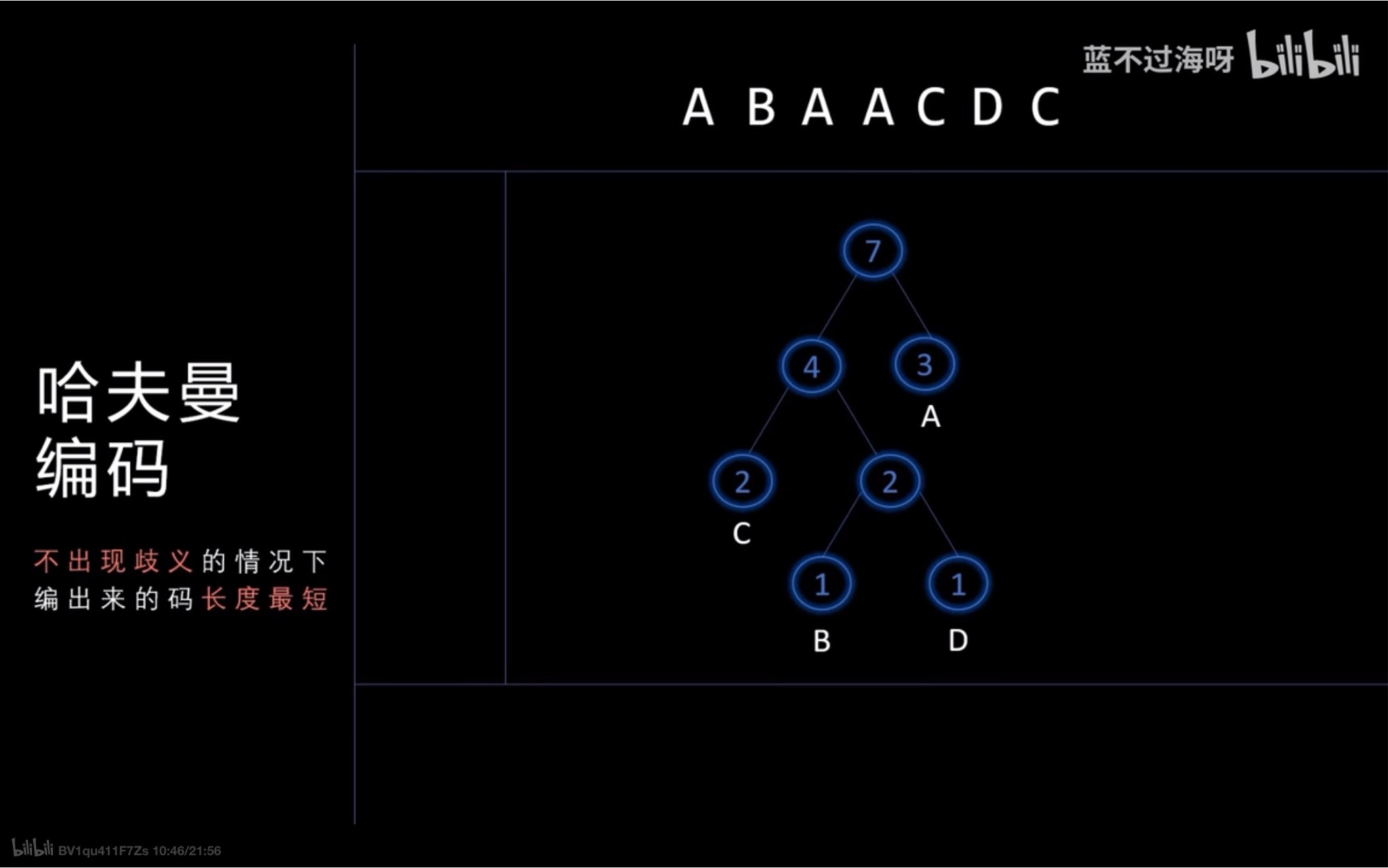
- 根据给边赋上权值 左0右1 得到每个字母的哈夫曼编码
- 这样能够保证编出来的码是最短的 没有歧义的(可以被正确解码)

散列表
散列函数的构造
直接定址法
- 这种方式是不适用于关键字不连续的情况的 因为如果关键字离散分布 那么就需要浪费较多的空间 例如下图当中 我们仅仅是六个离散的关键字就需要开辟72个空间来存储 这是非常浪费空间资源的
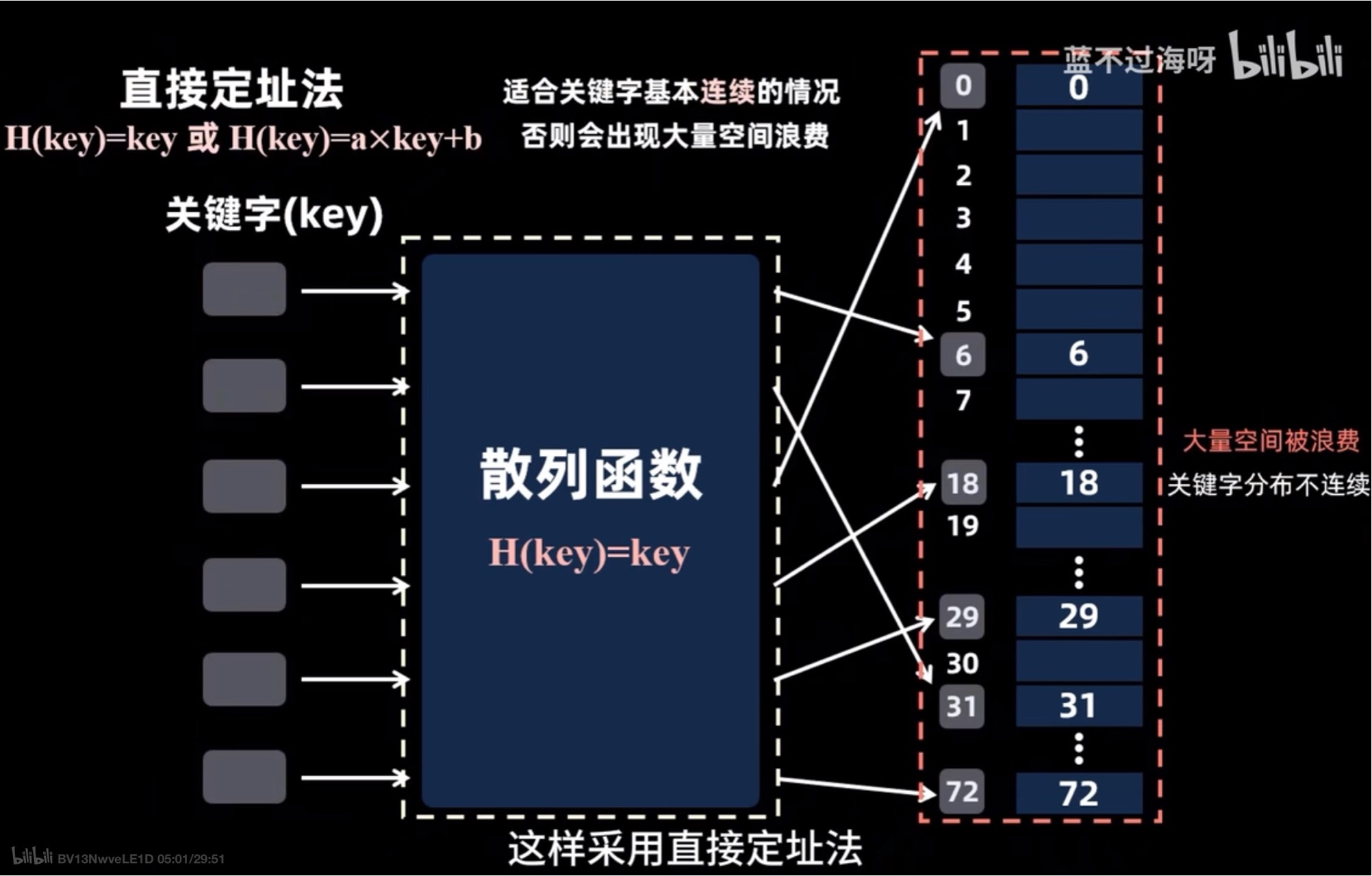
除留取余法

冲突处理
开放定址法
线性探测法
- 线性探测法其实是非常简单的 因为就是在出现映射冲突的时候一个一个地往前找一旦找到表尾就跳到表头继续
- 这个时候就可以解答前面的一个疑惑了 就是本身正常来说对于11取余数是不会映射到11上的 但是这里却留了一个位置出来就是在映射冲突这里起作用 也就是说很有可能会发生某个关键字发生冲突之后使用线性探测法放到了11这里
- 也就是完全有可能本应映射到对应位置上的关键字 但是由于线性探测法的存在就跑到别的位置上去了

性能计算 (ASL)
- 对于成功的情况 我们需要关注的是每个关键字的比较次数 然后除以关键字总数就可以了
- 对于失败的情况 我们是以散列到的位置为单位的
- 这里需要注意的是 我们对于每个位置都需要去比较到空位置为止
- 为什么空位置也算一次比较次数呢 就是因为空位置上其实我们会设置一个特殊值(要求不包含关键字)
- 以29为例 如果映射到7这个位置上的关键字他想要出现查找失败的情况 我们需要比较到51后面的
- 其次我们不需要计算下表这个位置的次数因为任何数都不会直接映射到这个位置 只有可能是线性探测法 被迫放在这个位置

- 查找失败 ASL=(每个位置需要比较的次数之和)/可以散裂到的位置总数 (全部都是去掉下表11的)

删除元素
- 由于我们之前在查找某个元素的时候 如果对应映射位置上没有找到就会继续向前探测 如果探测到空位值上就表明查找失败了
- 所以我们在删除元素的时候如果直接删除的话 就会导致我们在查找的时候破坏我们的查找路径 所以为了防止这个现象 我们在删除位置上做一个标记 一般也会设为一个特殊值 在查找元素的时候就会直接继续向下探测

平方探测法
- 引入
- 在前面学习的线性探测法当中我们在计算查找失败的平均查找长度(ASL)的时候
- 查找长度最大的那几个位置 都是由于堆积导致的 所以就有了平方探测法 来降低查找失败的平均查找长度

拉链法
- 我们还是采用除留取余法来构造 只不过每个位置上都是一个空指针
- 但是映射到同一个位置上的元素我们可以采用指针的方式将他们串联起来
- 对于元素的查找是跟前面有所不同的 在对需要查找的元素取余之后 我们只需要顺着链表往下找就可以了
- 包括删除这里由于采用了链表的方式并不用跟开放定址法那里提到的两种方式一样 在删除位置上打标记而是直接删除就好了
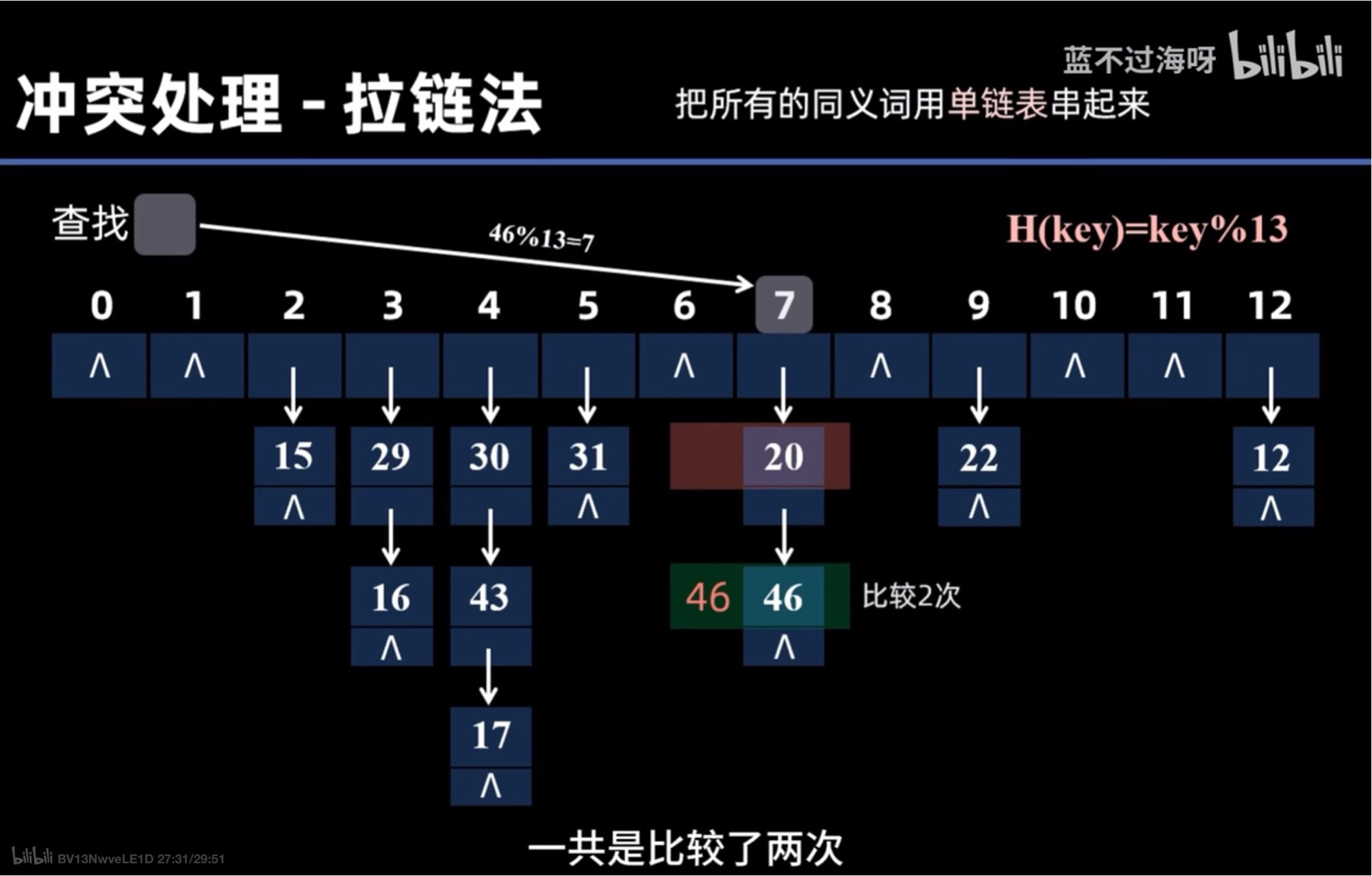
平均查找长度的计算
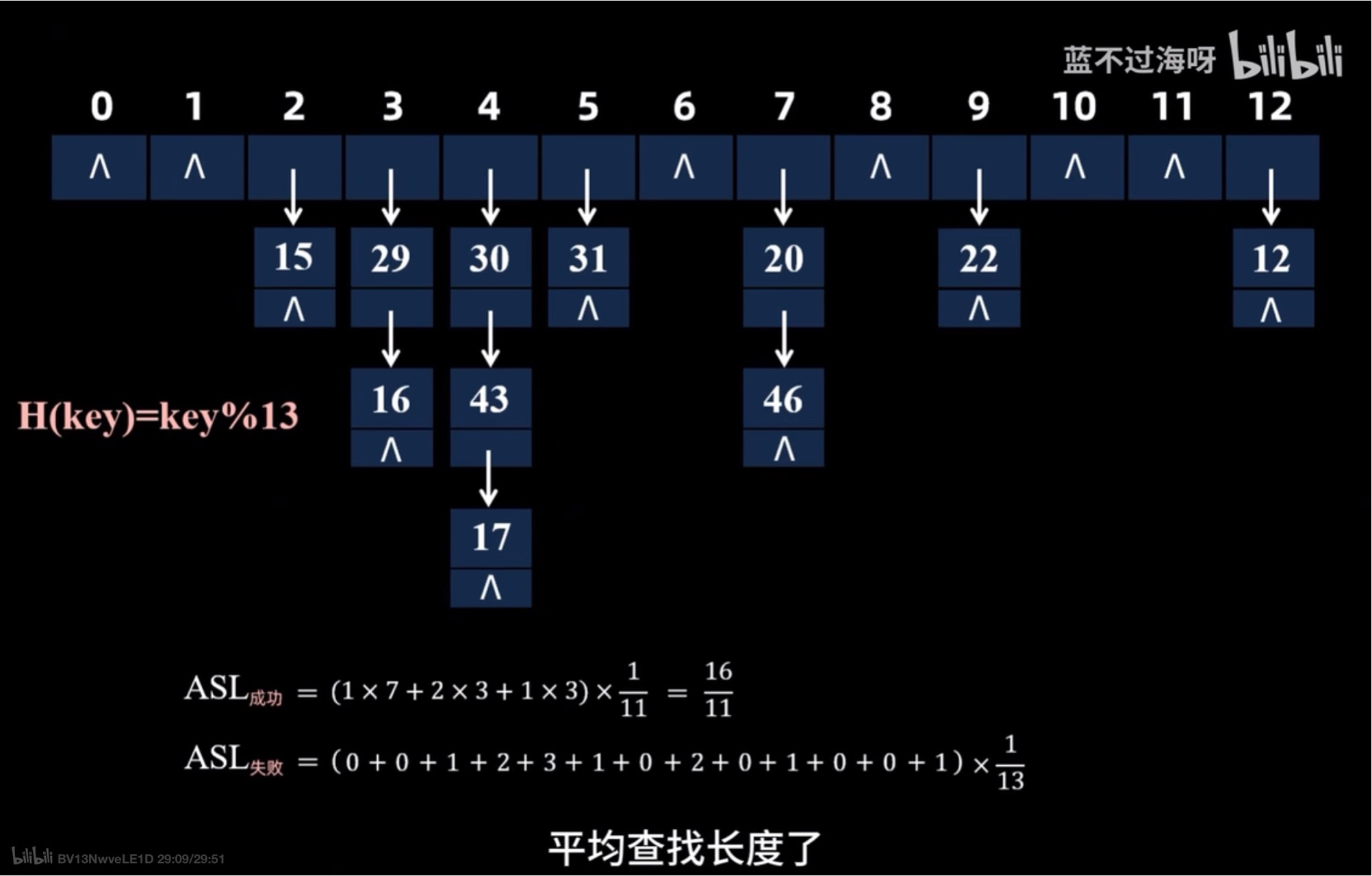
红黑树
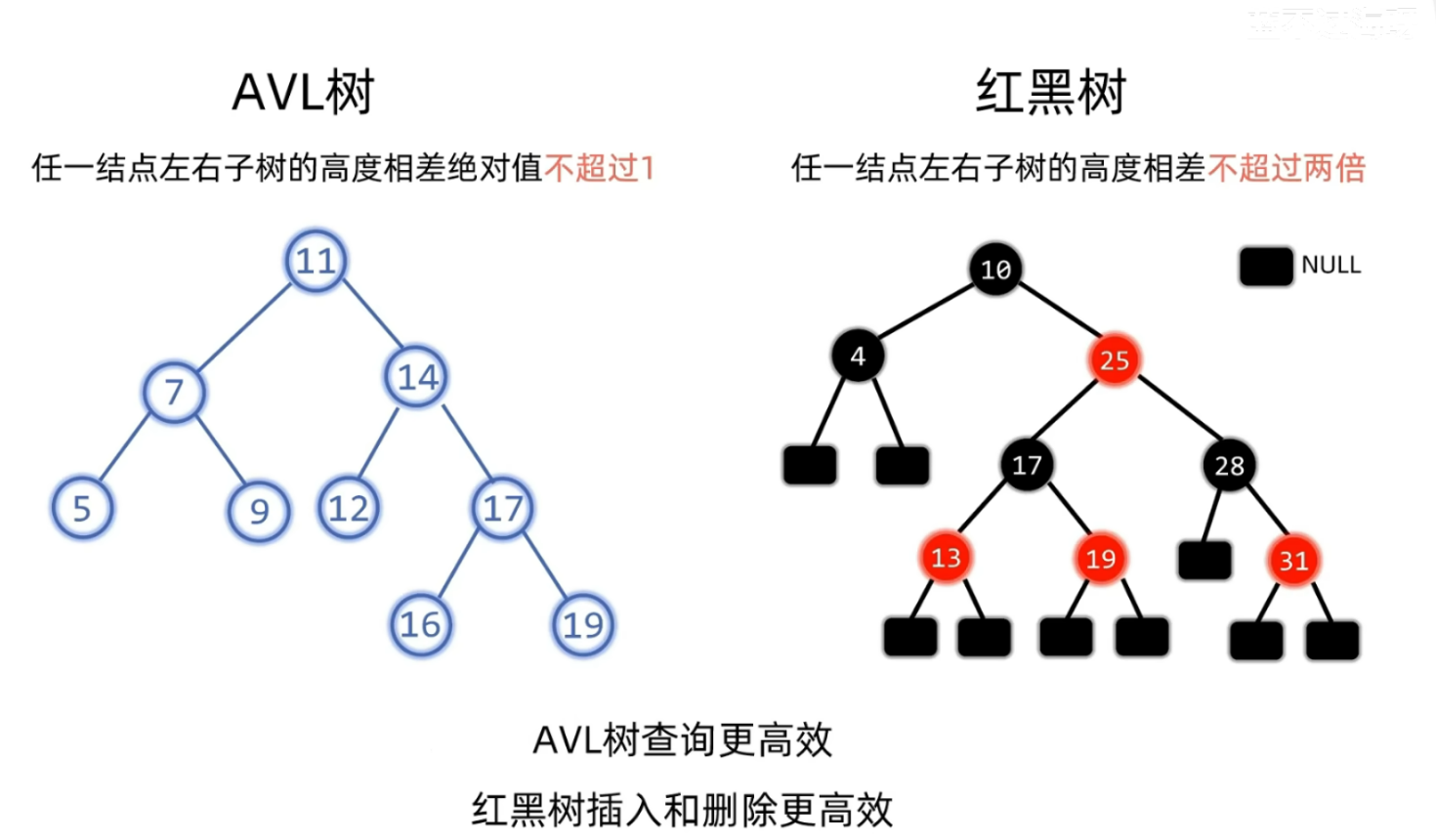
- 首先我们对于红黑树要有一个最基本的认知就是我们之前学习的平衡二叉树就是对于二叉排序树在极端情况下查找效率的优化(即当数据原本就有序的情况之下 我们所构建的二叉排序树是一颗斜树 从而它的查找效率就退化成了链表的查找效率O(N) 所以我们引入平衡二叉树来处理极端情况)
- 而对于红黑树本质上也是对于我们二叉排序树的优化 所以红黑树和AVL树的前提都得是一颗二叉排序树 即一定是满足左<根<右
- 只不过和二叉排序树的处理策略不一样罢了
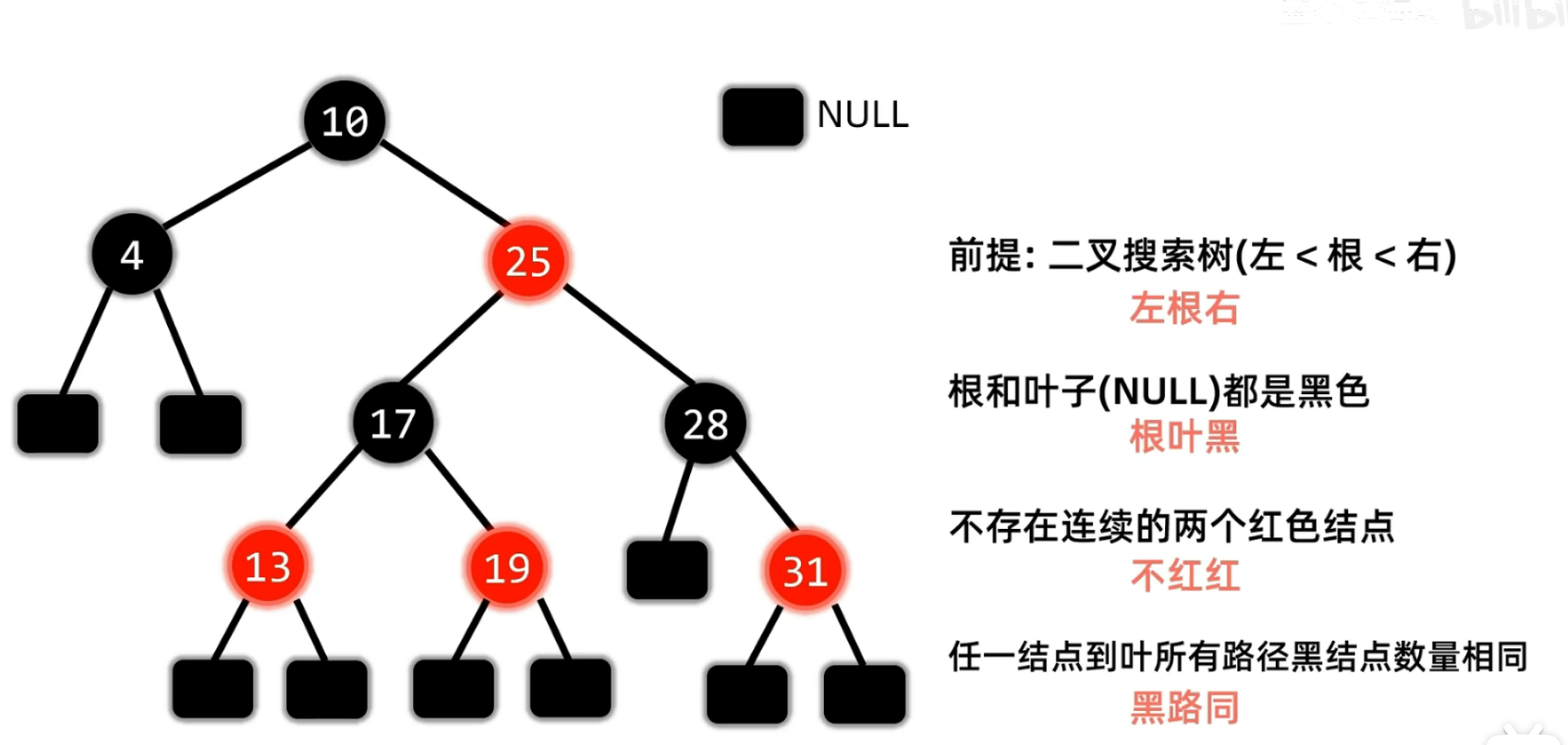
AVL树VS 红黑树
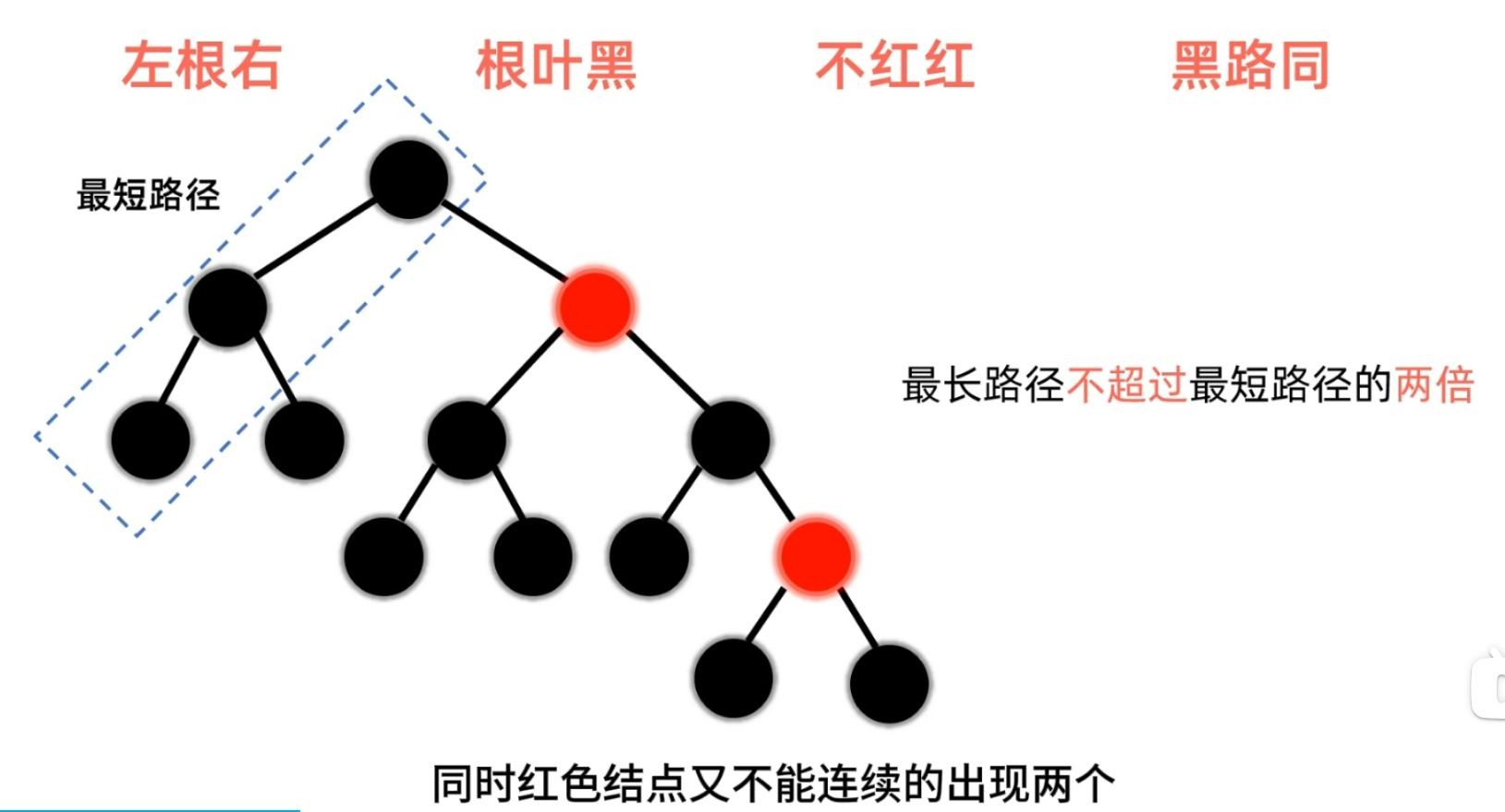
- 在这里我们需要知道的是平衡二叉树对于平衡的要求是比较严格的 所以在删除和查找方面效率是不如红黑树的
- 解释一下为什么在红黑树中左右子树的高度相差不超过两倍 ?
- 首先我们根据黑路同的性质可以知道根结点到每个叶子结点所经过的路径上黑色叶子结点个数相同
- 其次我们根据不红红的性质 也就是在一条路径上面不会出现连续的两个红色结点
- 所以假设目前这颗红黑树根结点到叶子结点所经过的黑色结点为3个
- 那么在保持这条性质的基础之上 最长的路径一定是黑 红 黑 红 黑 即任意结点的左右子树的高度相差最大不超过两倍
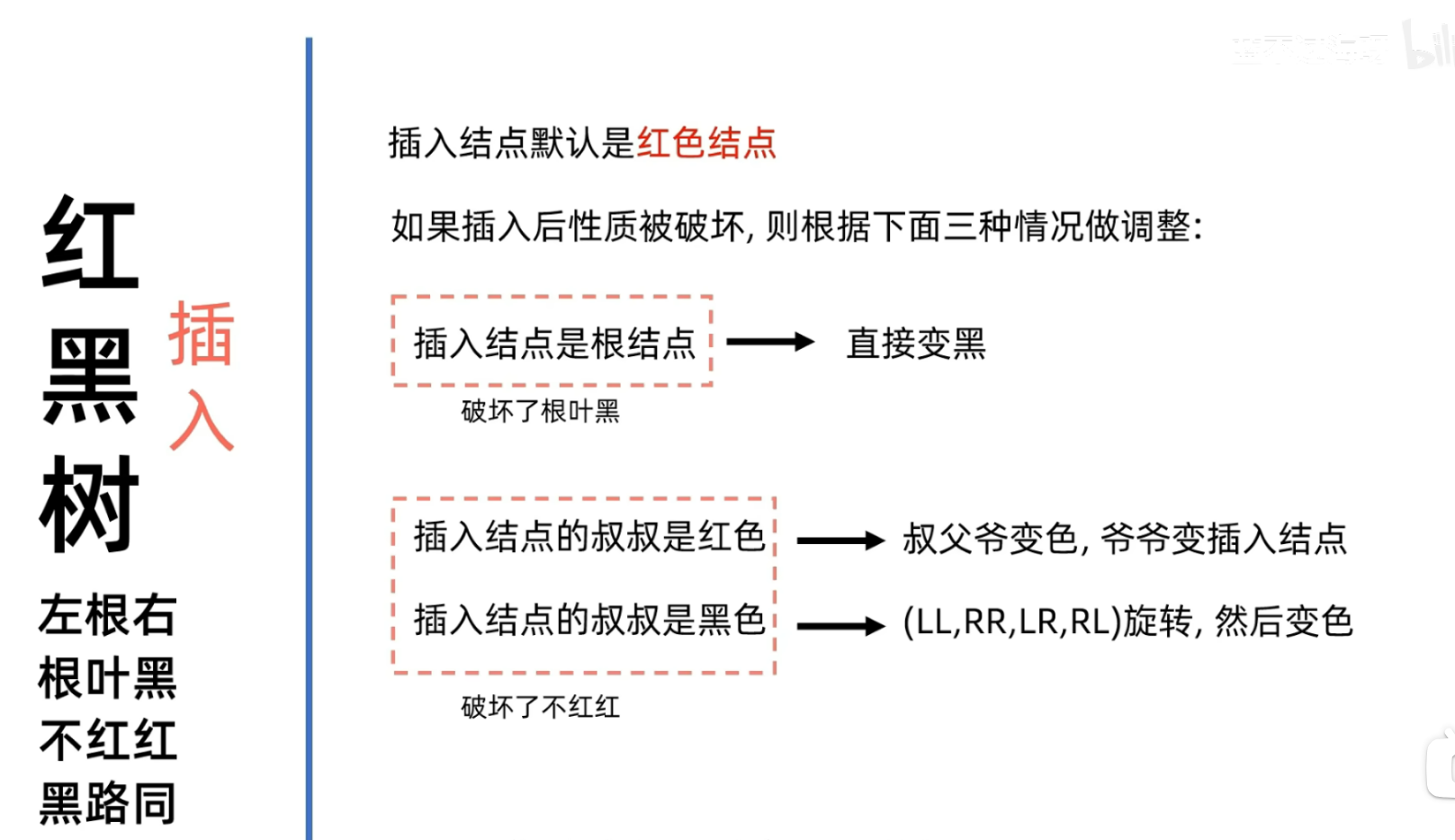
插入(重要)
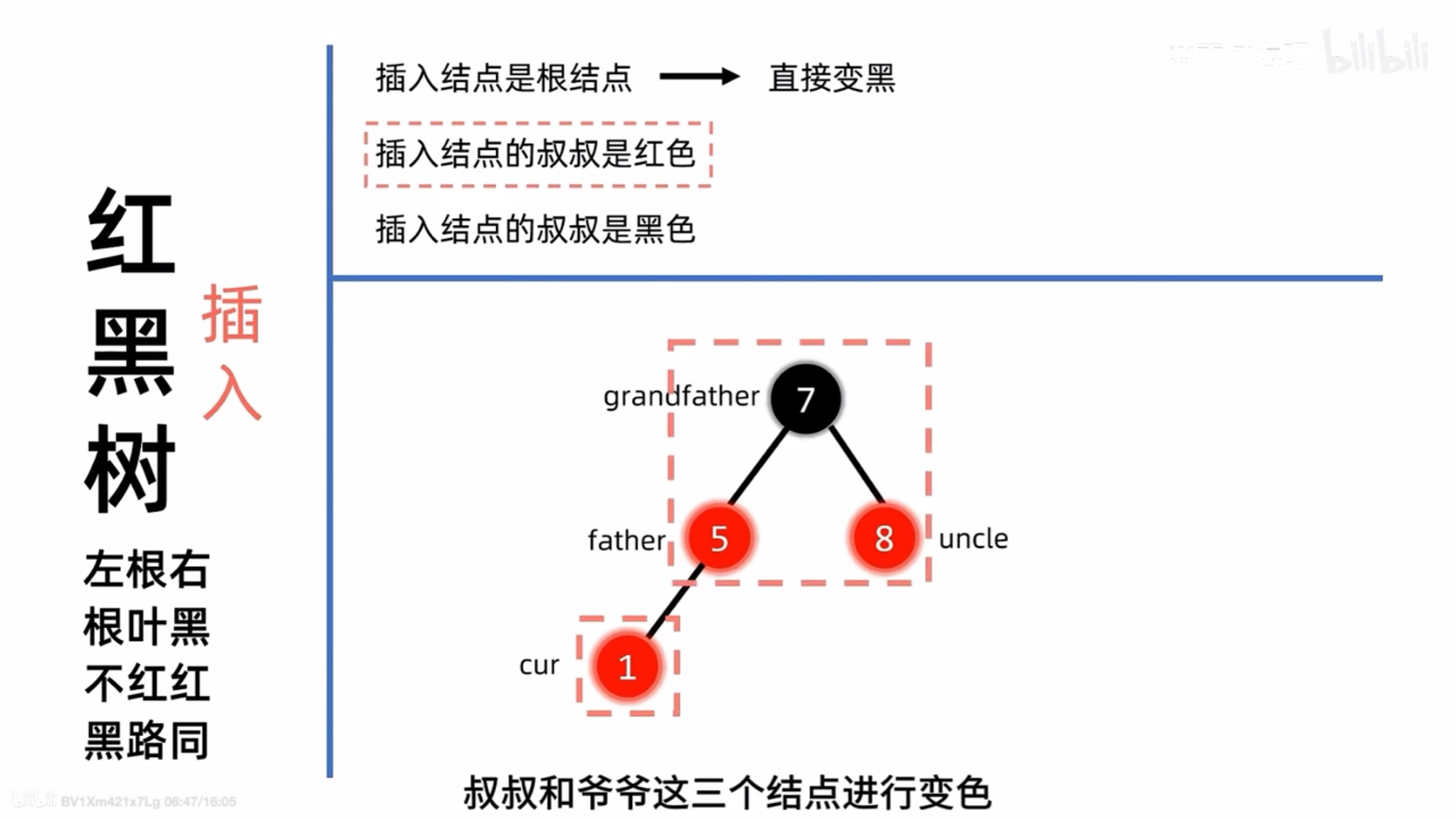
uncle结点为红的情况(可能需要调整两次)
- 这种情况在插入这里是需要我们特别注意的 因为之后我们要介绍的uncle结点如果为黑色 那么我们调整的方式是和AVL树当中LL RR LR RL型保持一致的 唯一不同的是我们需要检查每次调整过后是否违反了红黑树的四条性质
step 1
我们会对叔父爷变色 然后将爷爷变成插入结点 即我们会再次检查爷爷是否满足红黑树的性质
所以在前面提到需要调整两次
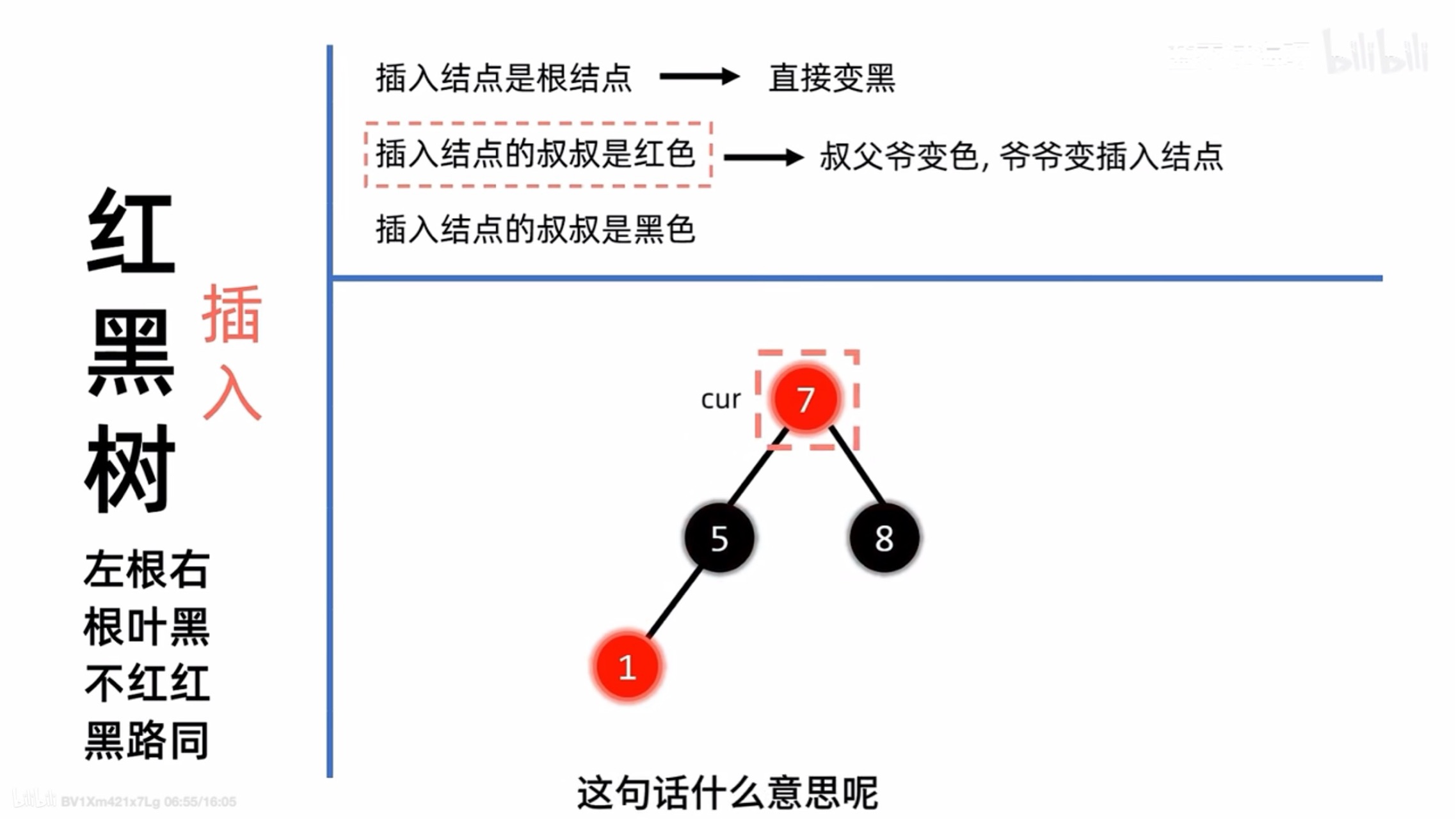
step 2
就是检查爷爷是否满足要求 如果不满足就去看爷爷的uncle结点然后再次处理(当然如果爷爷是根结点 那么我们只需要检查是否为黑色 即是否符合根叶黑的性质)
uncle结点为黑色的情况
step 1
对于叔叔是黑色结点的情况我们首要目的就是判断类型 发生问题的结点是位于什么位置 比如说 如果是根结点左孩子的右子树 那么就是LR型 调整方法其实在前面已经说过了 即先左旋左孩子 然后右旋爷爷
构建一颗红黑树的完整过程
B树
- 由来
- 我们每次寻找节点进行比较 而每次比较都需要由CPU去处理 而CPU是无法跟硬盘进行直接交互的
- 也就意味着我们必须将信息读入内存才可以 而访问硬盘这个操作是很耗时的
- 即为了解决平衡二叉树查找数据访问硬盘次数过多的问题
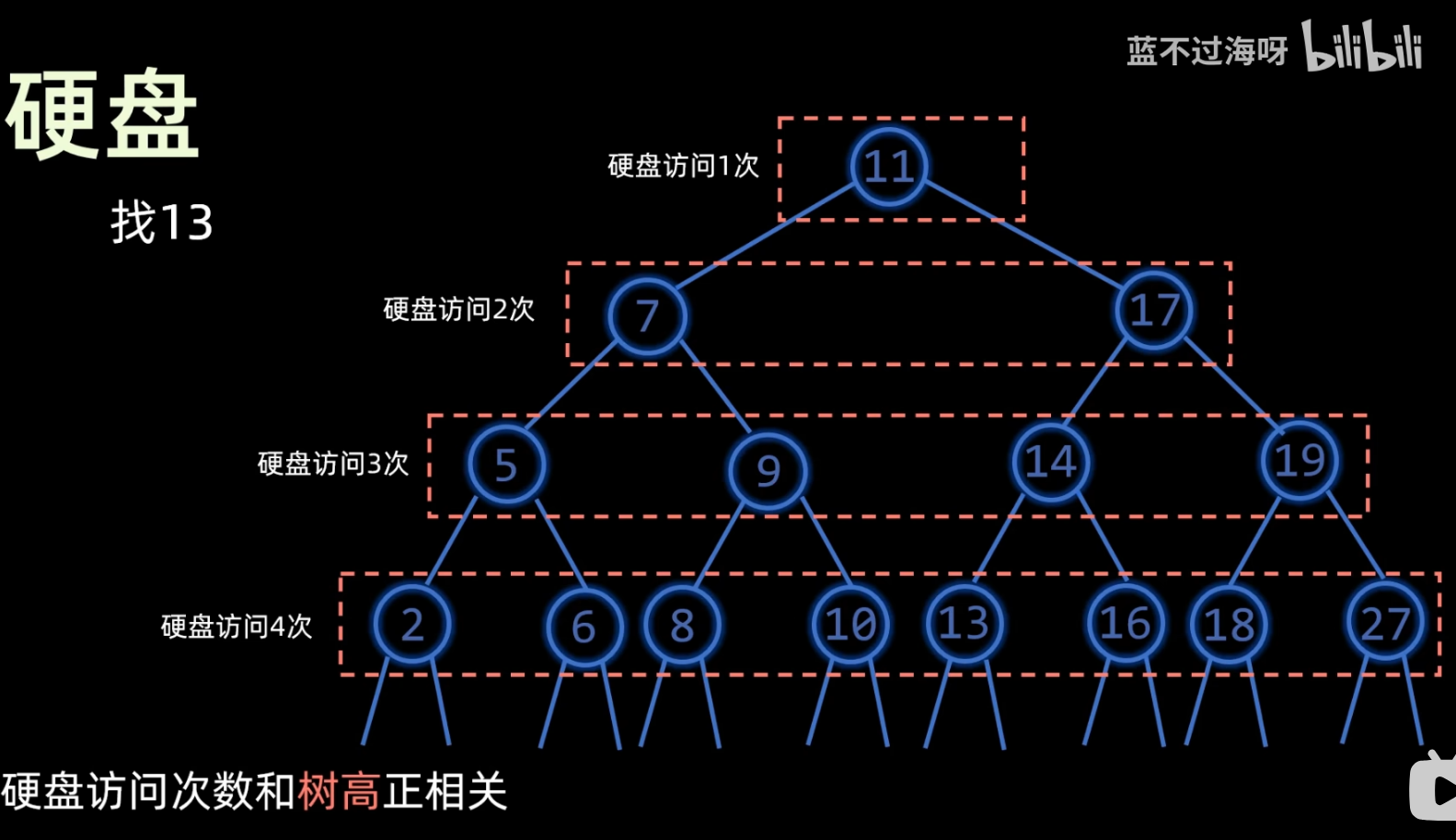
- 也就是说我们现在只需要将树高尽可能降低就能减少我们的硬盘访问次数
- 于是我们利用磁盘连续读取速度快的特性 使得一个节点存储多个数据 从而达到降低树高的目的
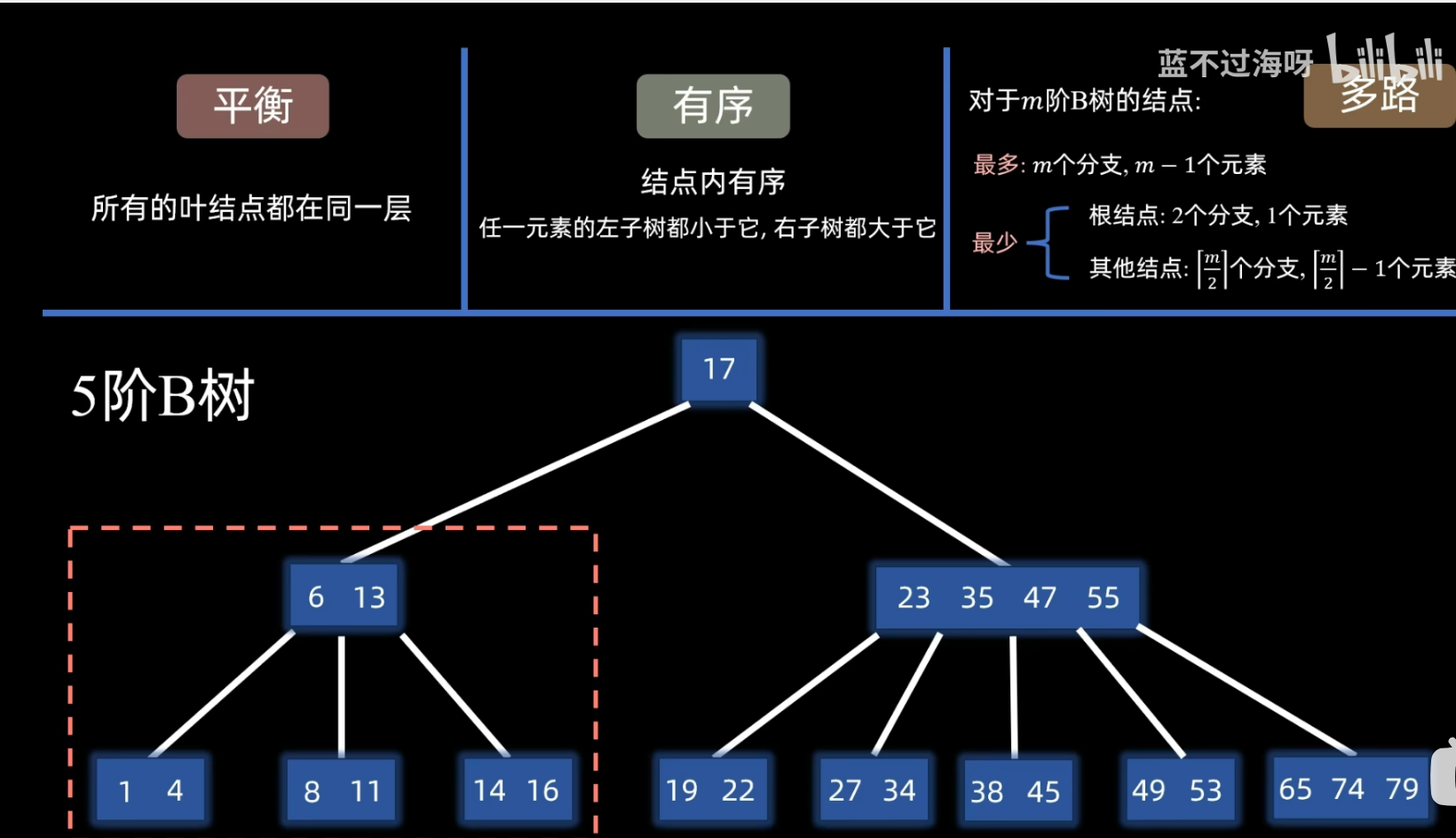
- 此时就可以将我们的这棵树看成 多叉 平衡 搜索树 ------B树
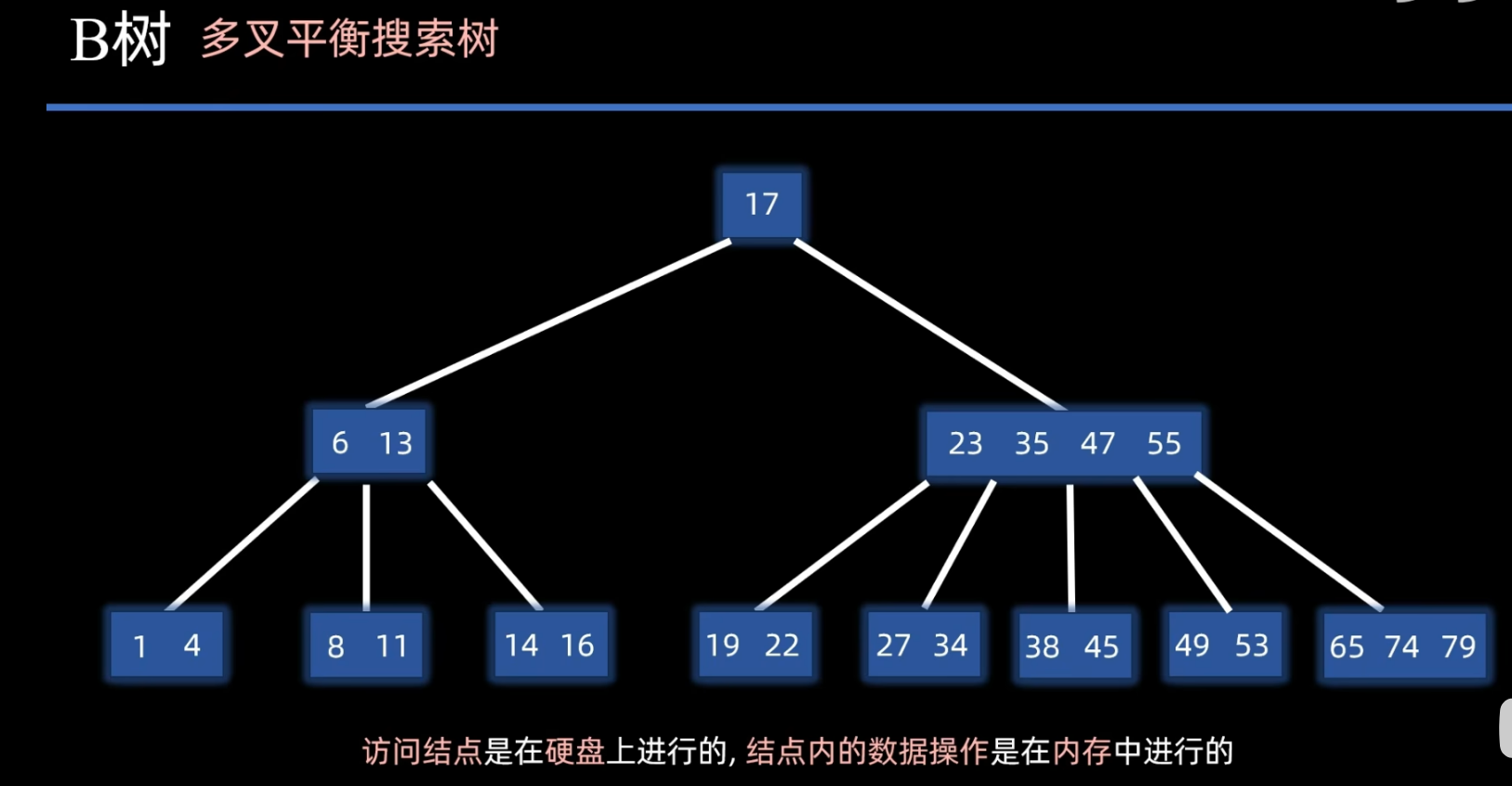
- (分别对应其三个特性------平衡 有序 多路)
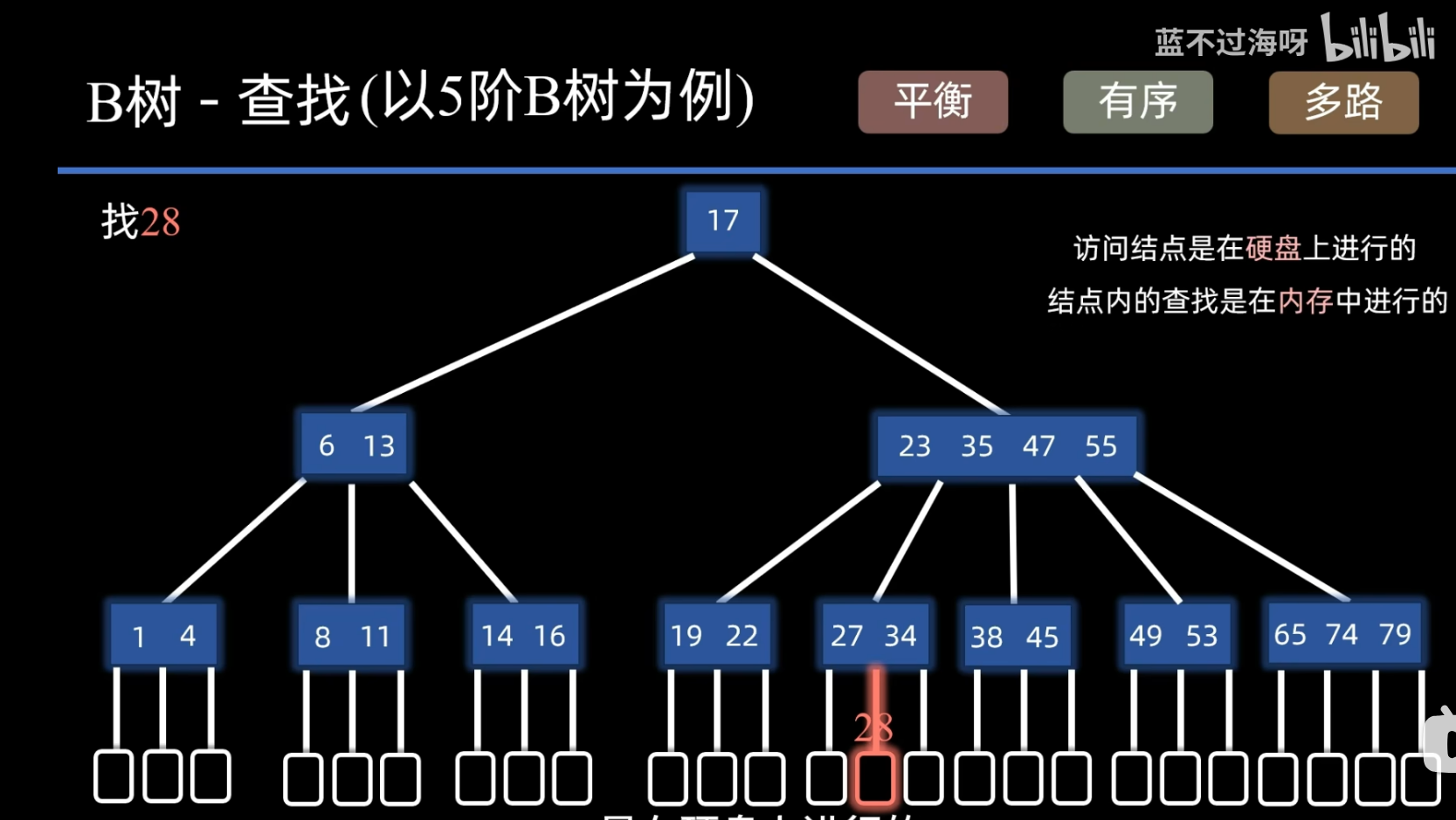
查找(类二叉搜索树)
- 查找失败就会走到失败节点上
插入
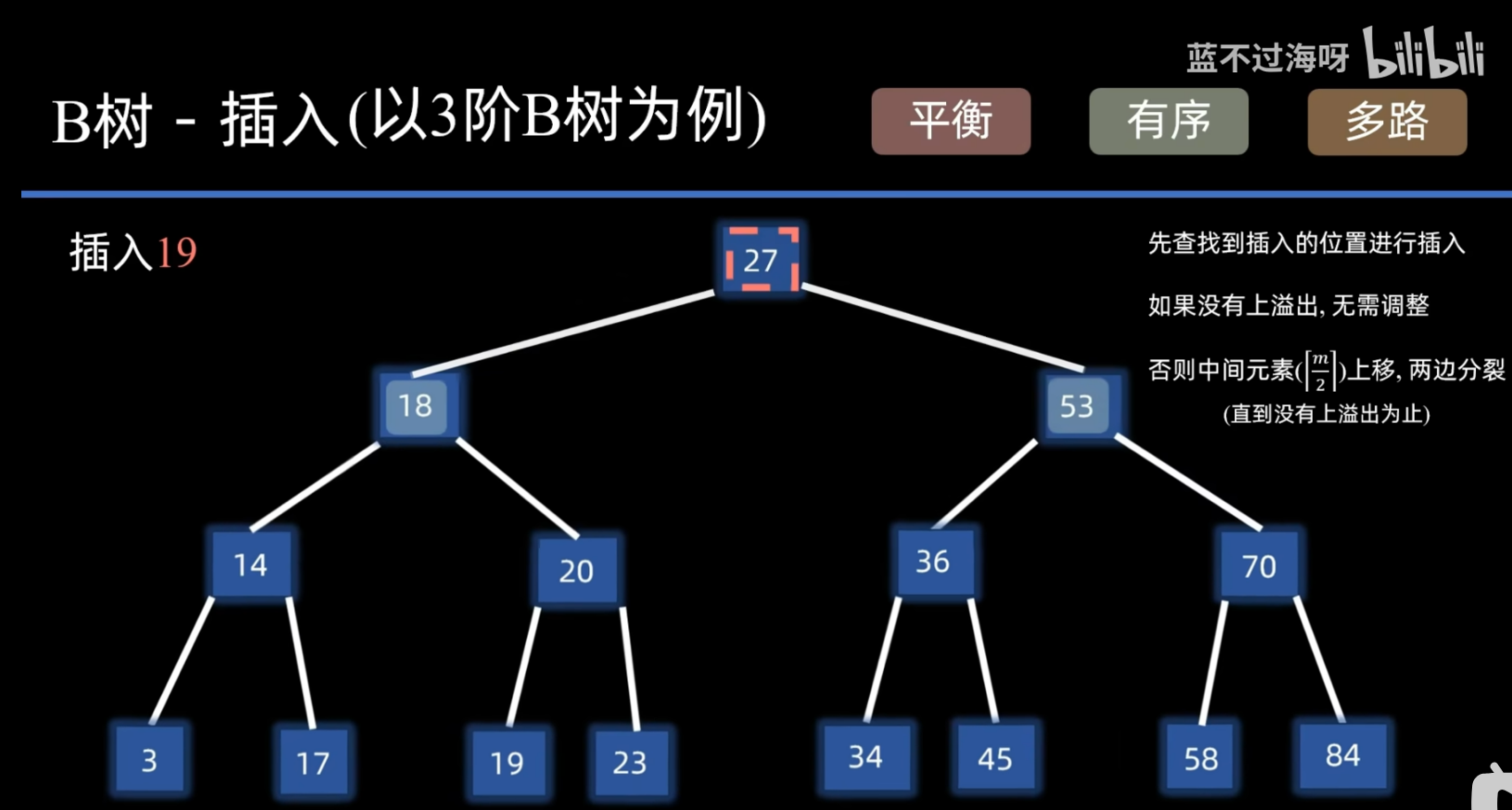
- 这个过程是比较形象的 如果忘记了的话还是建议去看一下视频
- 这个相比删除是比较简单的
- 只需要先搞清楚这个到底是几阶B树 这是我们判断溢出的基础
- 值得注意的是 我们的插入操作是有可能需要多次调整的 但是每次调整的手段都是比较单一
- 就是取中间元素然后两边分裂开来
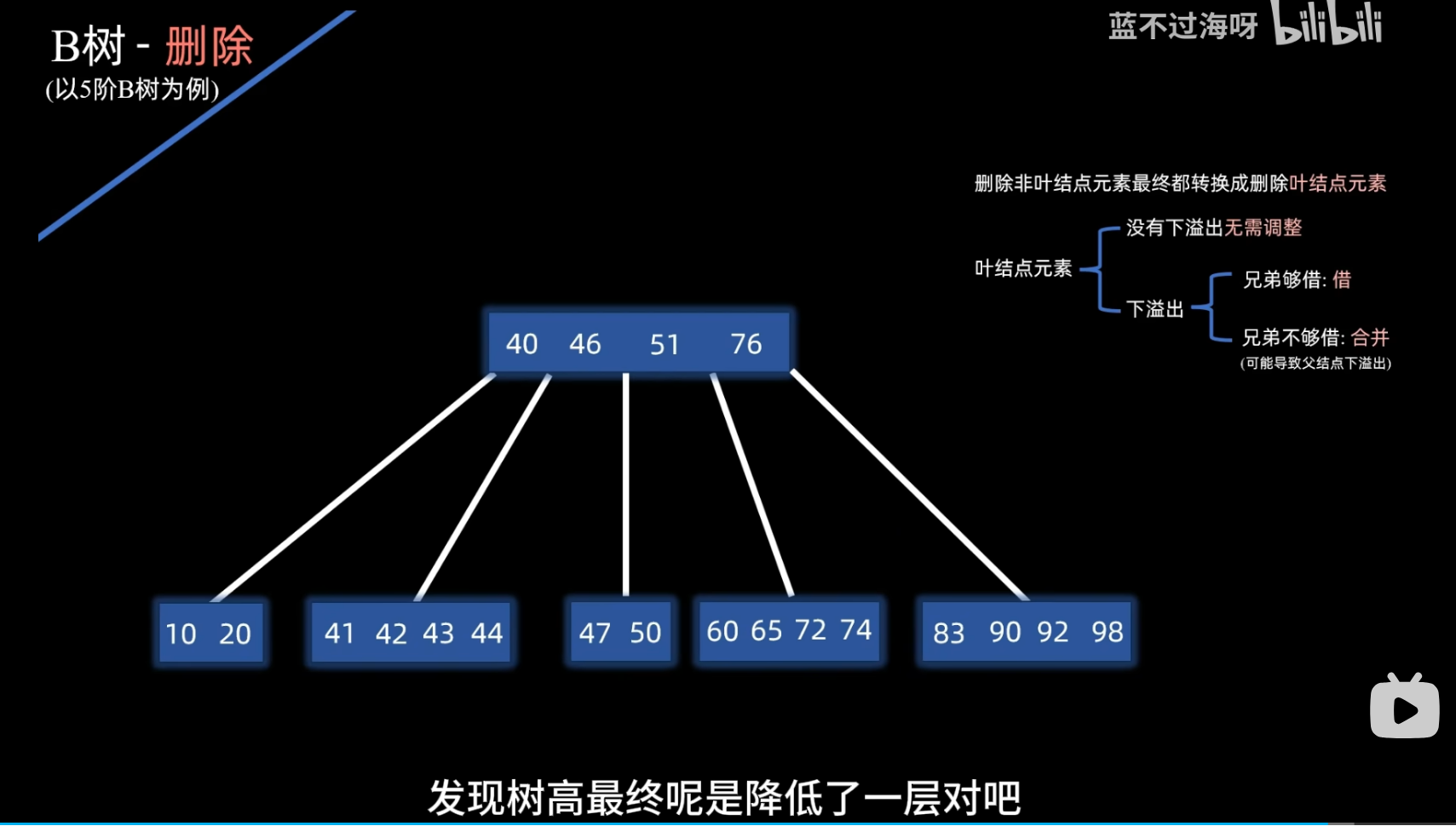
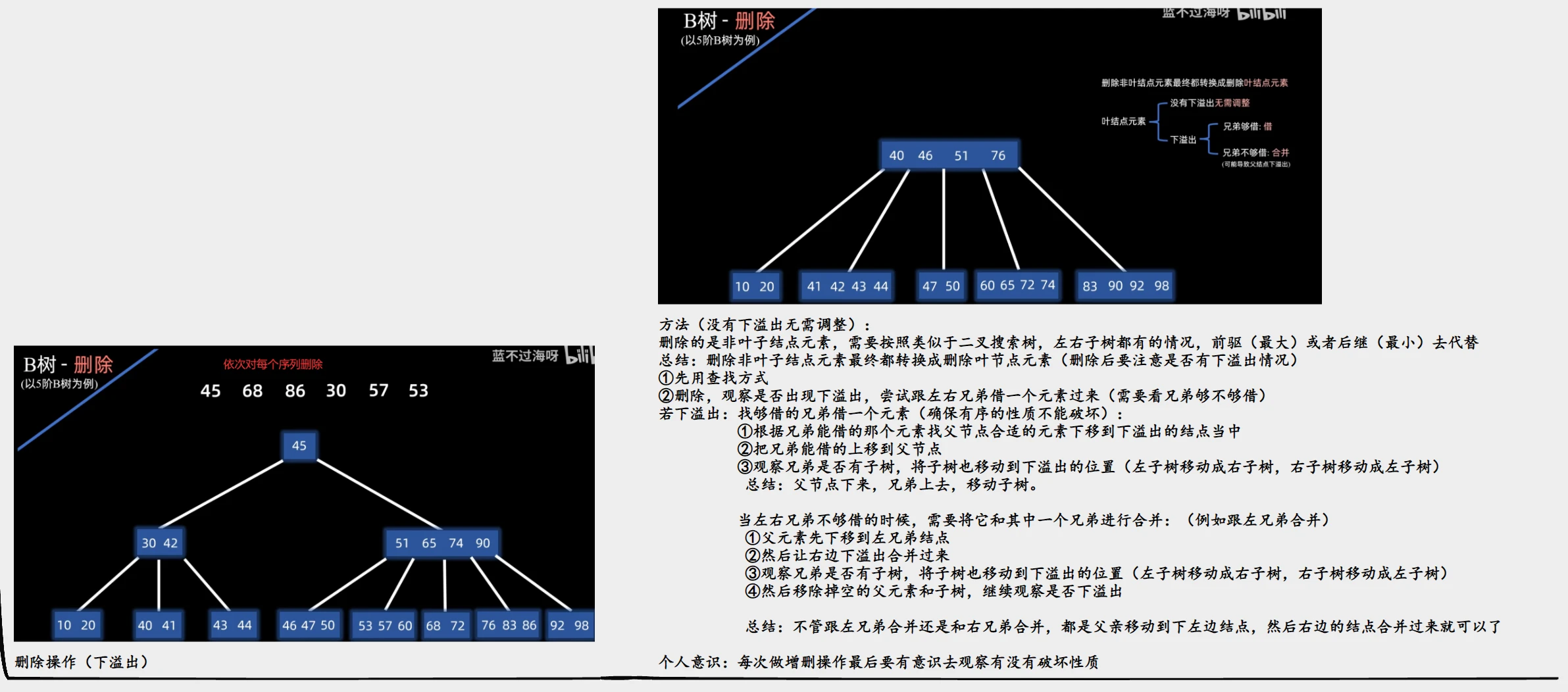
删除
- 什么叫下溢出 举个例子来说就是 对于5阶B树而言 他每个节点至少为------5/2上取整-1这么多个元素的
- 即每个节点至少需要两个元素
- 那么删除就非常有可能导致一个节点里面元素少于2个 这就叫做下溢出
B+树
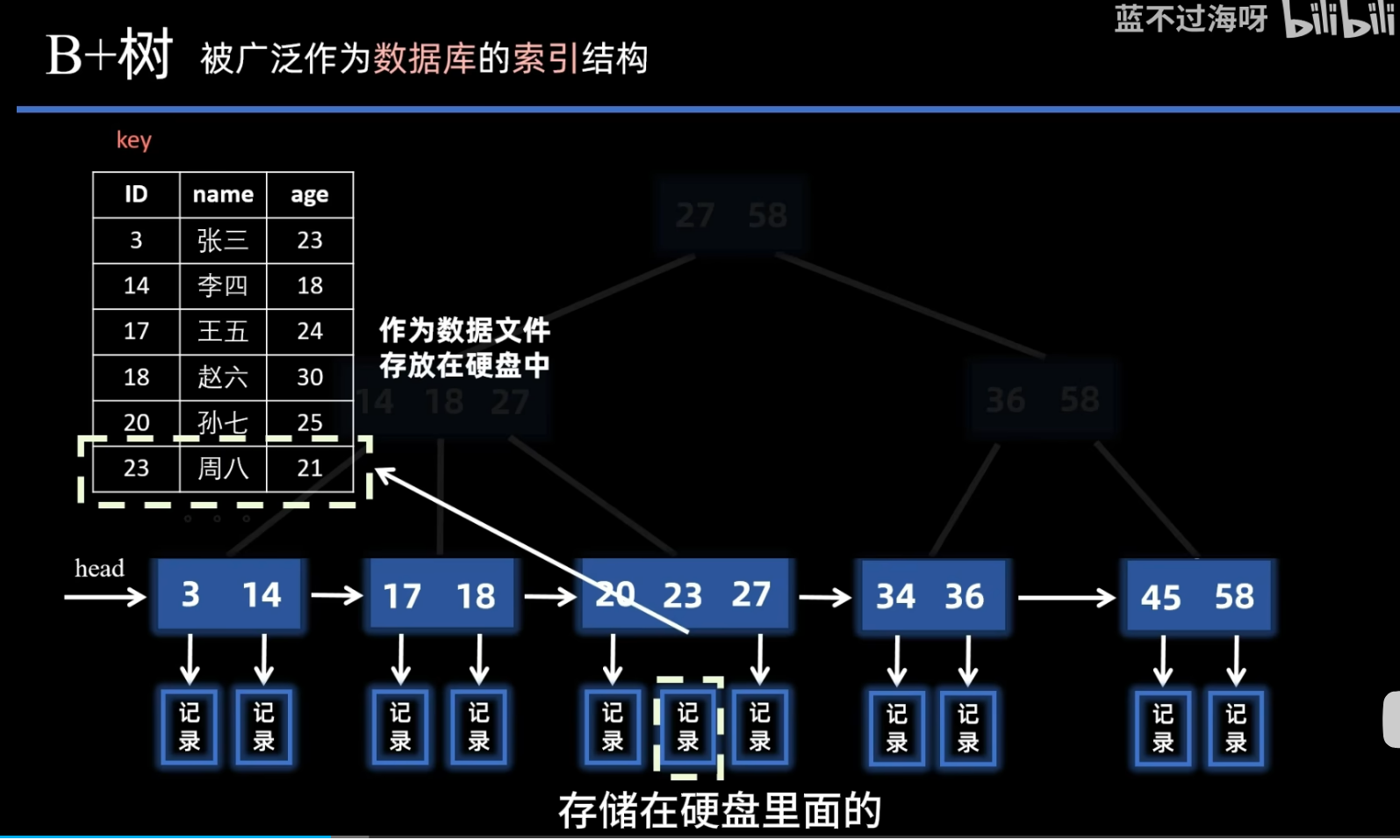
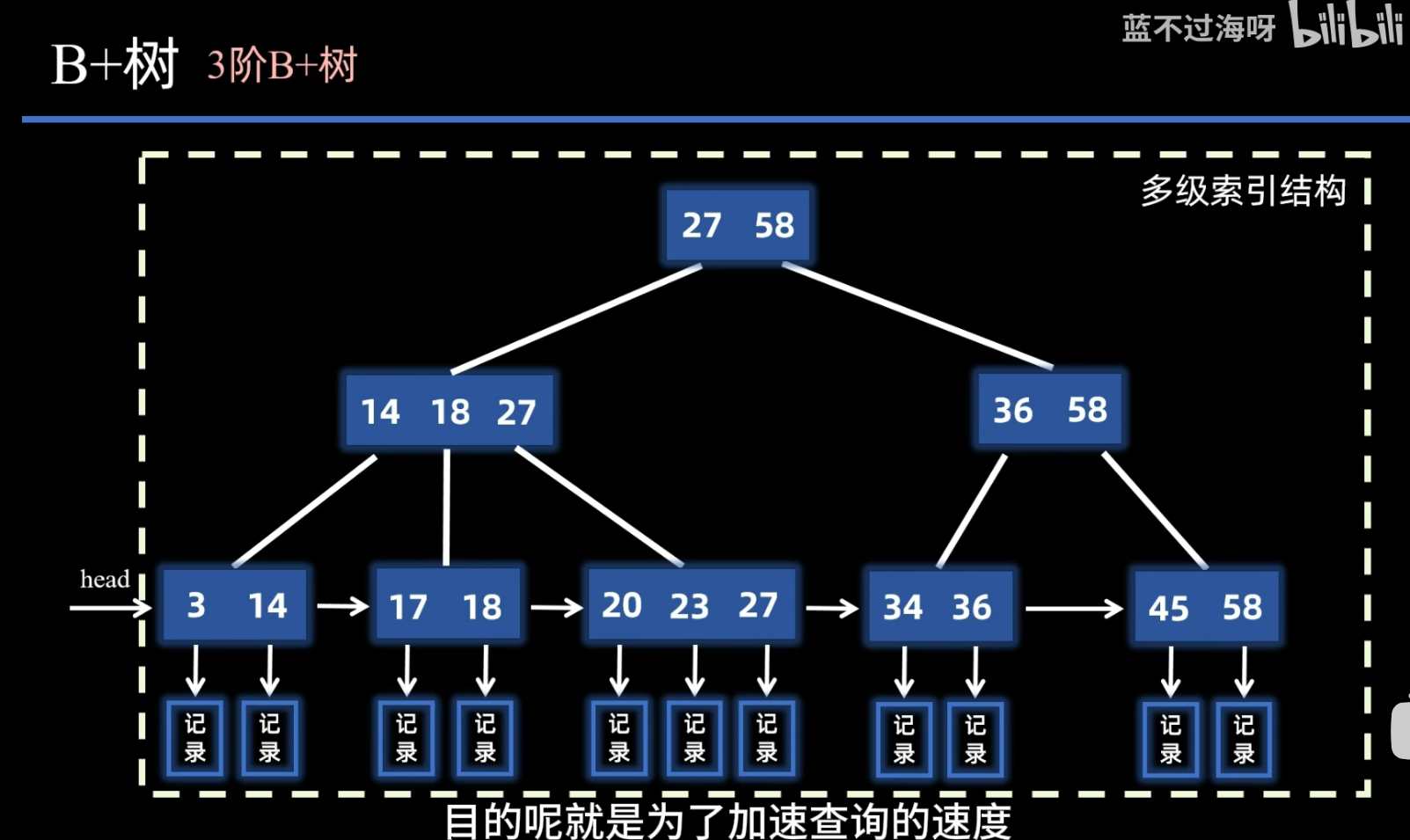
B树 VS B+树