UFlow：像素级工业零件异常检测 Normalized Flow 方法

什么是 Normalized FLow 方法：

通过一系列连续的、可逆的映射函数，将一个简单的概率分布映射成一个复杂的目标分布。

在异常检测应用当中，则是采用其逆过程，将未知的特征分布映射成已知的多元高斯分布。具体来说，学习一个强大的、可逆的变换函数，这个函数能将正常样本那 未知的、复杂的特征分布 ，精确地 "变换"或"映射" 到一个简单的、我们熟知的高斯分布上。

在测试阶段，正常样本的特征能被成功变换到目标高斯分布中；而 异常样本的特征则无法完成这个变换，其结果会严重偏离目标高斯分布 ，这个"偏离程度"就是异常分数。

而 UFlow 方法创新性地引入了 U-Net 结构，并且在推理阶段引入了 a contrario 框架，有效提高了异常检测的性能。

模型训练阶段

现在我们从头开始构建一下 U-Flow 框架。

特征提取: U-FLow 编码器

这个训练任务是单类别任务，意味着我们只选取正常数据进行训练。

假设我们现在有一批数据,首先，我们将所有的图片裁剪、伸缩成 448x448 的大小，并且将像素值从 [0, 255] 归一化到 [0.0, 1.0]。注意，此处使用ImageNet的均值和标准差对张量进行标准化，因为我们的特征提取器是在ImageNet上预训练的。

经过预处理并打包成批次（Batch）后，输入模型的数据形状为：[B, 3, 448, 448]。

多尺度特征提取

得到预处理后的数据，我们便要利用特征提取器提取它们的特征，U-flow 创新性地用了两个特征提取器，一个用于提取高分辨率特征，目的是细节观察；一个用于提取低分辨率路径，目的是全局观察。

高分辨率路径 (细节观察) ： extractor1 (cait_m48_448)。

这个路径用了 CaiT 系列的 cait_m48_448模型，接受 448x448 尺寸的图片，设定的 patch 大小是 16x16，特征维度是 768。因此一张图片能得到 768 张 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 448 / 16 ) × ( 448 / 16 ) = 28 × 28 (448/16) \times (448/16) = 28 \times 28 </math>(448/16)×(448/16)=28×28 尺寸大小的特征图。

此时,原始数据经过高分辨率路径的特征提取,形状变为 [B, 768, 28, 28]。

低分辨率路径 (全局观察) ：extractor2 (cait_s24_224)。

这个路径采用一个更小的 CaiT 模型：cait_s24_224，它接受 224x224 尺寸的图像，设定的 patch 大小也是 16x16, 特征维度更小 384。

因此，预处理的数据需要首先被双三次插值下采样 到224x224，形状变为 [B, 3, 224, 224]，然后被提取出 384 张 14x14 的特征图。输出形状 :为[B, 384, 14, 14]。

U-Flow 解码器

这是我们需要从头训练的核心部分。它接收编码器提取的特征，并通过一系列可逆变换将其映射到一个简单的标准正态分布。

阶段1：最粗糙的尺度/ U-Net 最底层

它接收来自 extractor2 的低分辨率的全局特征。这个全局特征位于 U-Net 的最底层。

首先，这个低分辨率特征会经过该尺度下的流模块 (Flow Stage) 处理。

流模块

在深入细节前，先来讲述一下 Normalized FLow 的基本原理：NF可以将一个复杂的分布映射到一个已知的简单的分布上，并且这个映射具有可逆性，即从这个简单分布上采样一点，可以逆变换成正常样本。

用一个通用的公式来表达：X 是未知的原分布，Z 是标准正态分布，而 <math xmlns="http://www.w3.org/1998/Math/MathML"> f θ f_{\theta} </math>fθ 即为 Normalized flow 变换。

<math xmlns="http://www.w3.org/1998/Math/MathML"> log ⁡ p X ( x ) = log ⁡ p Z ( f θ ( x ) ) + log ⁡ ∣ det ⁡ ∂ f θ ( x ) ∂ x ∣ \log p_X(x)=\log p_Z\left(f_\theta(x)\right)+\log \left|\operatorname{det} \frac{\partial f_\theta(x)}{\partial x}\right| </math>logpX(x)=logpZ(fθ(x))+log det∂x∂fθ(x)

由于 <math xmlns="http://www.w3.org/1998/Math/MathML"> p X p_X </math>pX 未知，我们训练一个 <math xmlns="http://www.w3.org/1998/Math/MathML"> f θ f_{\theta} </math>fθ 模型，来估计 p_X，因此我们的目标是：对于正常图片，得到的 p_X 尽可能高；对于异常图片，得到的 p_X 尽可能低。

利用这个原理，我们可以很方便的构建损失函数，但是唯一缺点就是直接计算行列式计算量巨大，所以NF采用了一种便于计算雅可比行列式的模型架构。

它将输入特征 x 分成两份, x1, x2。x1 对应的输出 y1 直接等于 x1，x2 对应的输出 y2 则由 x1 计算而来。

x1 经过第一层会输出两个因子，一个用于缩放 (scale) ，记作 s；另一个用于平移 (translate)，记作 t。
y2 = s * x2 + t
y1，y2 再拼成 y，此时 y 对 x 的雅可比行列式直接等于 s。

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> y = [ y 1 , y 2 ] = [ x 1 , s ⋅ x 2 + t ] , [ s , t ] = g ( x 1 ) ∂ y ∂ x = y = [y_1 , y_2] = [x_1, s\cdot x_2 + t], [s, t] = g(x_1)\\ \frac{\partial{y}}{\partial{x}} = </math>y=[y1,y2]=[x1,s⋅x2+t],[s,t]=g(x1)∂x∂y=

为了让模型更加复杂，上面描述的网络可以继续叠加。

y 先经过确定可逆的洗牌过程，得到 y_shuffle, 再将 y_shuffle 拆分成两个部分，重复上面的过程。

回到我们的例子，我们得到了低分辨率特征，形状为[B, C, H, W]=[B, 384, 14, 14]。

第1步，分裂。在通道维度 (C) 上将输入张量 x 一分为二，得到 x_a 和 x_b。输出 x_a: [B, 192, 14, 14]， x_b: [B, 192, 14, 14]。

第2步：冻结与处理：

冻结 x_a : 我们暂时不对 x_a 做任何事情，直接让它"流"过去。
处理 x_b : 将 x_b 送入一个任意复杂的、普通的神经网络 （比如几层卷积）。这个网络不需要是可逆的，它可以是任何标准的CNN。这个网络的任务是学习并输出两个参数张量： s，t。s 和 t 的形状和 x_a 完全相同，均为[B, 192, 14, 14]。

第3步，变换。变换的方式是一个非常简单的仿射变换（Affine Transformation）。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> y a = x a ⊙ exp ⁡ ( s ) + t y_a=x_a \odot \exp (s)+t </math>ya=xa⊙exp(s)+t

这里的 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⊙ \odot </math>⊙ 表示逐元素相乘。
使用 <math xmlns="http://www.w3.org/1998/Math/MathML"> exp ⁡ ( s ) \exp (s) </math>exp(s) 是为了保证缩放因子恒为正。

第4步，合并。最后，我们将变换后的 y_a 和完全没有被改变 的 x_b (我们令 y_b = x_b) 重新在通道维度上拼接起来。因此，形状重新回到 [B, 384, 14, 14], 这就是生成的第一个隐变量 <math xmlns="http://www.w3.org/1998/Math/MathML"> z 1 z_1 </math>z1.

与此同时，我们已经可以非常简单地计算出这次变换的 LJD （雅各比行列式）。对于这个仿射变换，LJD 就是所有缩放因子 s 之和（因为log(exp(s))=s），即 LJD = sum(s)，记此时的 LJD 为 ljd_1.

阶段2：可逆上采样过程

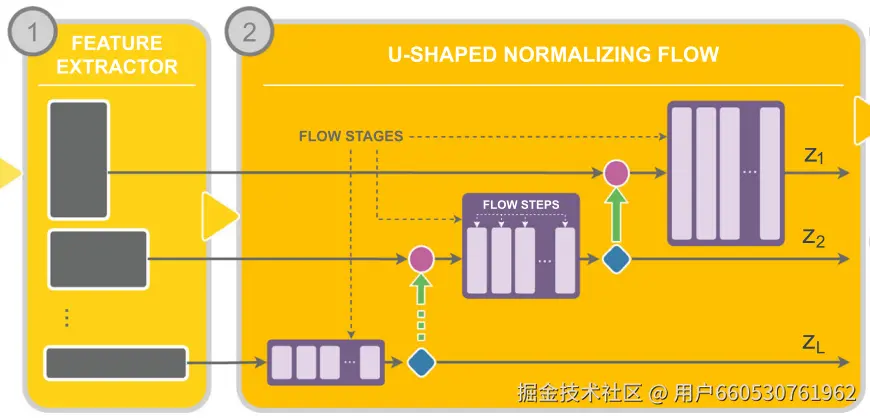
这一步用到了 U-Net 的核心，便是将全局特征开始上采样并且和细节特征进行融合。

将来自阶段1的"半成品"进行上采样，使其空间维度匹配高分辨率特征。上采样通过一种"挤压"操作的逆操作实现，即减少通道数，扩大空间尺寸。这一步不是用简单的 reshape 操作完成，而是通过一个上采样的操作，感兴趣可以去看源码。

输入形状: [B, 192, 14, 14]
输出形状: [B, 192/4, 14*2, 14*2] -> [B, 48, 28, 28]

接下来，将经过上采样的特征和来自extractor1 的高分辨的特征通过跳跃连接进行拼接。

拼接物1 (来自底层的上采样特征): [B, 48, 28, 28] + 拼接物2 (来自高分辨的特征): [B, 768, 28, 28]。

因此，拼接后形状为 [B, 48+768, 28, 28] -> [B, 816, 28, 28].这个就是生成的第二个隐变量 <math xmlns="http://www.w3.org/1998/Math/MathML"> z 2 z_2 </math>z2

然后，将拼接后的特征送入本阶段的流模块：

和上一个 NF 框架相同，输出形状保持不变，[B, 816, 28, 28]。与此同时，需要计算并累加该阶段的 LJD，我们称之为 ljd_2。

最终输出 (z_fine) : 由于这是最精细的尺度，不再进行分裂。整个输出都成为最终的隐变量。形状: [B, 816, 28, 28]

模型最终输出 : 我们得到了两个隐变量张量 z_coarse 和 z_fine，以及总的对数雅可比行列式 LJD_total = ljd_1 + ljd_2。

构建损失函数

我们的目标是让模型学会正常数据的分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> p X ( x ) p_X(x) </math>pX(x) 。我们通过最大似然估计（Maximum Likelihood Estimation）来实现这一点，即调整模型参数 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ 来最大化观测到我们训练数据的概率。

这等价于最小化负对数似然（Negative Log－Likelihood，NLL）：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Loss = − log ⁡ p X ( x ) \text { Loss }=-\log p_X(x) </math> Loss =−logpX(x)

根据归一化流的变量替换公式，我们可以将被建模的复杂分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> p X ( x ) p_X(x) </math>pX(x) 转换到简单的隐空间分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> p Z ( z ) p_Z(z) </math>pZ(z) ：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> log ⁡ p X ( x ) = log ⁡ p Z ( f ( x ) ) + log ⁡ ∣ det ⁡ ( J f ( x ) ) ∣ \log p_X(x)=\log p_Z(f(x))+\log \left|\operatorname{det}\left(J_f(x)\right)\right| </math>logpX(x)=logpZ(f(x))+log∣det(Jf(x))∣

<math xmlns="http://www.w3.org/1998/Math/MathML"> z = f ( x ) z=f(x) </math>z=f(x) 是模型的可逆变换。
<math xmlns="http://www.w3.org/1998/Math/MathML"> p Z ( z ) p_Z(z) </math>pZ(z) 是隐变量 <math xmlns="http://www.w3.org/1998/Math/MathML"> z z </math>z 的概率密度，我们假设它服从标准正态分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> N ( 0 , I ) \mathcal{N}(0, I) </math>N(0,I) 。
<math xmlns="http://www.w3.org/1998/Math/MathML"> log ⁡ ∣ det ⁡ ( J f ( x ) ) ∣ \log \left|\operatorname{det}\left(J_f(x)\right)\right| </math>log∣det(Jf(x))∣ 就是模型在各个流模块中计算并累加的总LJD。

对于标准正态分布，其对数概率密度为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> log ⁡ p Z ( z ) = − d 2 log ⁡ ( 2 π ) − 1 2 ∑ i = 1 d z i 2 \log p_Z(z)=-\frac{d}{2} \log (2 \pi)-\frac{1}{2} \sum_{i=1}^d z_i^2 </math>logpZ(z)=−2dlog(2π)−21i=1∑dzi2

其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 是 <math xmlns="http://www.w3.org/1998/Math/MathML"> z z </math>z 的维度。在优化中，常数项可以忽略，所以 <math xmlns="http://www.w3.org/1998/Math/MathML"> log ⁡ p Z ( z ) \log p_Z(z) </math>logpZ(z) 正比于 <math xmlns="http://www.w3.org/1998/Math/MathML"> − 1 2 ∥ z ∥ 2 2 -\frac{1}{2}\|z\|2^2 </math>−21∥z∥22 。将这些代入我们的损失函数：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Loss = − ( log ⁡ p Z ( z ) + L J D total ) ≈ − ( − 1 2 ∥ z ∥ 2 2 + L J D total ) \text { Loss }=-\left(\log p_Z(z)+L J D{\text {total }}\right) \approx-\left(-\frac{1}{2}\|z\|2^2+L J D{\text {total }}\right) </math> Loss =−(logpZ(z)+LJDtotal )≈−(−21∥z∥22+LJDtotal )
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Loss = 1 2 ∥ z ∥ 2 2 − L J D total \text { Loss }=\frac{1}{2}\|z\|2^2-L J D{\text {total }} </math> Loss =21∥z∥22−LJDtotal

具体到我们的数据，我们需要计算所有隐变量（ <math xmlns="http://www.w3.org/1998/Math/MathML"> z coarse z_\text{coarse} </math>zcoarse 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> z fine z_\text{fine} </math>zfine）的能量项（L2范数的平方），并将它们加起来。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> L P Z total = 1 2 ∥ z coarse ∥ 2 2 + 1 2 ∥ z fine ∥ 2 2 LPZ_{\text {total }} = \frac{1}{2}\|z_\text{coarse}\|2^2 + \frac{1}{2}\|z\text{fine}\|_2^2 </math>LPZtotal =21∥zcoarse∥22+21∥zfine∥22

最终，我们在一个批次上计算的平均损失为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> L o s s batch = 1 B ∑ batch ( L P Z total − L J D total ) \mathrm{Loss}{\text {batch }}=\frac{1}{B} \sum{\text {batch }}\left(L P Z_{\text {total }}-L J D_{\text {total }}\right) </math>Lossbatch =B1batch ∑(LPZtotal −LJDtotal )

模型推理阶段

前文提到，对于经典的 Normalized Flow 方法，在测试阶段，正常样本的特征能被成功变换到目标高斯分布中；而 异常样本的特征则无法完成这个变换，其结果会严重偏离目标高斯分布 ，这个"偏离程度"就是异常分数。

U-flow 创新地引入了 A Contrario 框架。

异常热力图：Likelihood-Based

这一步的目的就是将 U-Flow 解码器输出的、人类无法直接理解的隐空间特征 z，转换成一张我们肉眼可见的、直观的"异常热力图 (Anomaly Map)"** 。

我们将待测试阶段经过提取特征 -> UFlow 模型处理得到两个隐变量z_coarse 和 z_fine，它们的大小一个是 [384, 14, 14]，一个是 [816, 28, 28]。这里先将它们统一记作 z。

隐变量 z 经过双线性上采样 后得到 <math xmlns="http://www.w3.org/1998/Math/MathML"> z ~ \tilde{z} </math>z~，确保无论来自哪个尺度，它都和原始输入图像 H x W 一样大,假设最终它有 C 个通道.

再次注意标准正态分布，其对数概率密度为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> log ⁡ p Z ( z ) = − d 2 log ⁡ ( 2 π ) − 1 2 ∑ i = 1 d z i 2 \log p_Z(z)=-\frac{d}{2} \log (2 \pi)-\frac{1}{2} \sum_{i=1}^d z_i^2 </math>logpZ(z)=−2dlog(2π)−21i=1∑dzi2

依然舍弃常数项，采纳平方项用于估算异常得分.

对于某个特定像素位置 (i,j)，由于上采样后 <math xmlns="http://www.w3.org/1998/Math/MathML"> z ^ \hat{z} </math>z^ 有 C 个通道，因此将该位置的所有通道上的平方加起来，并且最后取平均，得到当前尺度下的该位置的对数概率:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> − 1 C ∑ k = 1 C ( z ~ i j k ) 2 -\frac{1}{ C} \sum_{k=1}^{C}\left(\tilde{z}_{i j k}\right)^2 </math>−C1k=1∑C(z~ijk)2

然后取指数，将它还原成标准高斯分布的概率密度:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> exp ⁡ ( − 1 2 C ∑ k = 1 C ( z ~ i j k l ) 2 ) \exp \left(-\frac{1}{2 C} \sum_{k=1}^{C}\left(\tilde{z}_{i j k}^l\right)^2\right) </math>exp(−2C1k=1∑C(z~ijkl)2)

最后，计算所有尺度在该位置的概率密度，然后取平均，得到该位置最终的概率。这个概率大致指代的是正常的概率有多大（值越接近 0.5，越靠近中心区域），因此用 1 减去它即为最后的异常概率。

最终公式为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> A S ( i , j ) = 1 − 1 L ∑ l = 1 L exp ⁡ ( − 1 2 C l ∑ k = 1 C l ( z ~ i j k l ) 2 ) A S(i, j)=1-\frac{1}{L} \sum_{l=1}^L \exp \left(-\frac{1}{2 C_l} \sum_{k=1}^{C_l}\left(\tilde{z}_{i j k}^l\right)^2\right) </math>AS(i,j)=1−L1l=1∑Lexp(−2Cl1k=1∑Cl(z~ijkl)2)

A contrario 方法

这个方法被用来找出异常区域，它引入了一套名为 "a contrario"（反证法） 的统计框架，来自动地、无监督地计算出一个有意义的阈值，从而得到最终的异常分割蒙版（Mask）。

要理解这个阶段，我们必须先理解 NFA（Number of False Alarms，误报数）这个概念。这个理论用了假设检验的思想，不试图去定义＂什么是异常＂（因为异常千奇百怪），而是反过来，去精确地定义＂什么是正常＂。这个＂正常＂的定义，就是零假设 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( H 0 ) \left(\mathcal{H}_0\right) </math>(H0) 即：热力图上的所有元素值都符合标准正态分布。

首先，我们会通过一种算法（下文讲）得到若干个候选的（连通的）异常区域。A Contrario 的目的就是去裁定这些异常区域是否是真的异常。

基于零假设，这些候选区域的元素值都满足标准正态分布，和上面计算热力图类似，根据在标准正态分布下这一条件，可以大致估算得它们是异常的概率，将它们相加求平均，得到最终的异常概率，记为 <math xmlns="http://www.w3.org/1998/Math/MathML"> Pr ⁡ H 0 ( E ) \operatorname{Pr}_{\mathcal{H}_0}(E) </math>PrH0(E).

这个异常概率如何计算的呢？

首先，他们没有直接使用第三阶段那个带有"启发式"成分的异常图，而是构造了一张新的、理论上更完美的图 u：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> u ( i , j ) = ∑ k = 1 C ( z i j k ) 2 u(i, j)=\sum_{k=1}^C\left(z_{i j k}\right)^2 </math>u(i,j)=k=1∑C(zijk)2

对于每个像素位置 (i,j)，将其在所有通道 k 上的隐空间特征 z 的 平方加起来 。我们知道，对于正常像素，每个 z 都是独立的标准正态分布 N(0,1)。C个独立的标准正态分布变量的平方和，服从自由度为C的卡方分布 <math xmlns="http://www.w3.org/1998/Math/MathML"> χ 2 ( C ) χ^2(C) </math>χ2(C)。然后根据这个卡方分布，我们精确地知道在正常情况下，图中每个像素值的概率分布！

通过这个概率分布，我们可以清楚的计算出这个区域是异常的概率，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> Pr ⁡ H 0 ( E ) \operatorname{Pr}_{\mathcal{H}_0}(E) </math>PrH0(E)。能直接对这个概率设定阈值来判定是否是异常区域么？显然这里忽略了纯粹因为巧合而出现这样的区域的情况。

举个极端的例子，448X448 的热力图（取值为0~1）出现了一个亮度为 0.9 的异常点，出现 0.9 的概率极低大概是 0.001，但是能认为这个异常点确实就是异常区域么，不能，因为也可能纯粹因为巧合，这张图可是有 448x448 <math xmlns="http://www.w3.org/1998/Math/MathML"> ≈ \approx </math>≈ 250000 个像素点，每个像素点都有 0.001 的概率出现 0.9 的亮度，因此从期望上看，这张热力图纯粹因为巧合都有可能出现 0.001 x 250000 = 250 个这样的异常点。因此这个异常点多半是个噪点。

因此对于一般的区域 L，图中一共可以找出多少类似 L 的区域呢(这个类似概念上扩充到了区域内像素点相同即可)？如果 L 的像素点一多，这种类似区域的个数显然是个很大的数目。文中用了一个 polynomies_size 近似方法，能很快的计算这个数目.将这个数目记作 <math xmlns="http://www.w3.org/1998/Math/MathML"> N T N_T </math>NT。

最后误报数 NFA 即为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> NFA ⁡ ( E ) = N T × Pr ⁡ H 0 ( E ) \operatorname{NFA}(E)=N_T \times \operatorname{Pr}_{\mathcal{H}_0}(E) </math>NFA(E)=NT×PrH0(E)

从上面的计算过程可以看出，NFA 的实际意义就是，假设该照片正常的情况下，出现的异常区域个数的期望。通常会设定 NFA 阈值为 1。如果 NFA = 0.1 表示一张图片出现 0.1 个这样的异常区域，换句话说每 10 张图片才会出现这样的异常。这么稀有的事件都发生了，表示这个区域是真的异常。

确定候选区域

想象一下 u( 是一张地形图，数值越大的地方山峰越高。水平集就是用水位线 λ 去"淹没"这张图，所有高于水位线的区域 u(i,j) ≥ λ 就构成了一个水平集。

在同一个水位线 λ 下，可能会有多个不相连的"岛屿"，每个岛屿就是一个连通组件，也就是我们的一个 候选异常区域 。

这些"岛屿"之间存在天然的父子关系。一个在很高水位线（λ很大）出现的小岛，必然被一个在较低水位线（λ较小）出现的大岛所包含。这种包含关系可以自然地组织成一棵树。通过构建这棵树，作者巧妙地将"测试所有可能的区域"这个无限问题，简化为了" 只测试树上这些有限的、最有希望的候选区域 "这个可行问题。

现在我们有了一系列候选区域（树上的节点），我们需要为每个区域计算其 PFA (Probability of False Alarm，误报概率) ，也就是 Pr(E | H_0)。

首先，计算单个正常像素的能量值 u(i,j) 偶然大于等于 λ 的概率是多少？这个概率 p 可以通过卡方分布的累积分布函数 (CDF) 精确得出：p = 1 - CDF_χ²(λ)。
然后，由于第二阶段保证了所有像素之间都是相互独立 的，那么一个包含 N (|L_{λ,c}|) 个像素的区域，所有像素 的能量值都偶然大于等于 λ 的概率，就是这 N 个独立事件同时发生的概率，即 p 的 N 次方。

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P F A ( L λ , c ) = ( 1 − C D F χ 2 ( λ ) ) ∣ L λ , c ∣ PFA(L_{λ,c}) = (1 - CDF_χ²(λ))^{|L_{λ,c}|} </math>PFA(Lλ,c)=(1−CDFχ2(λ))∣Lλ,c∣

这个公式非常精妙，它内含了一种"自我约束"的平衡机制，这使得它能很好地勾勒出异常的真实边界：

扩大区域 (|L| 变大)：指数 |L| 增大，会让PFA值急剧变小（更有可能是异常）。
但代价是 ：为了让区域包含更多的像素，通常需要降低水位线 λ。而 λ 减小，会让底数 (1 - CDF(λ)) 变大，这又会使PFA值变大（更不可能是异常）。

a contrario 检验会自动寻找那个让PFA最小的"最佳平衡点"，这个点对应的区域往往就是异常最真实的轮廓。