Transformer：多头自注意力机制详解 (PyTorch 实现)

1. 概述

多头自注意力（Multi-Head Self-Attention）是 Transformer 模型的核心组件，由论文《Attention Is All You Need》提出。它允许模型在处理序列数据时，同时关注来自不同位置、不同表示子空间的信息，从而高效地捕捉序列内部丰富的上下文依赖关系。

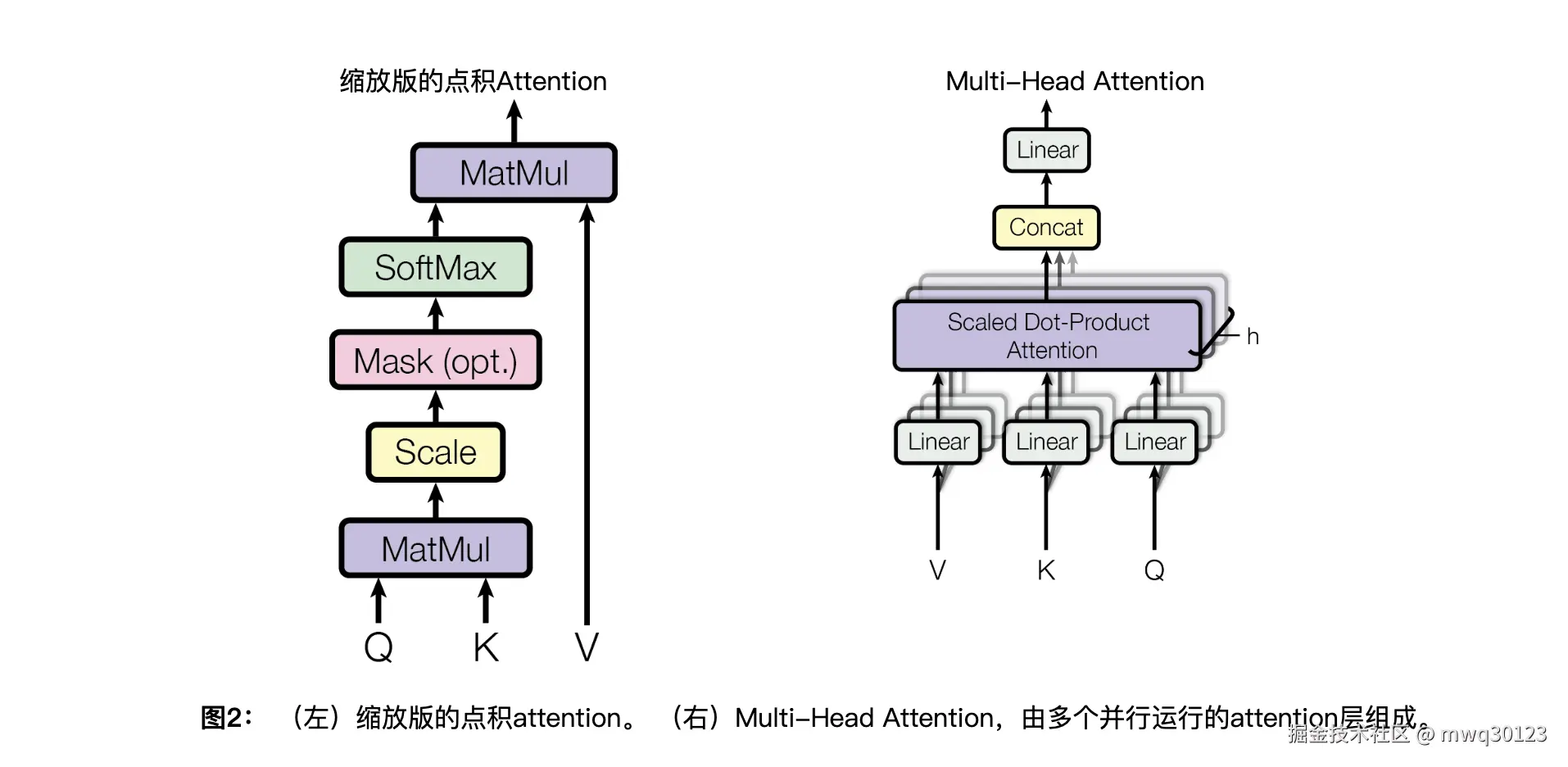本文档将详细拆解其在 PyTorch 中的计算流程，重点阐述张量（Tensor）在各个阶段的形状变换和具体操作。

2. 核心参数定义

在整个计算流程中，我们将使用以下符号来定义张量的维度：

符号	维度	描述
`b`	`batch_size`	批次大小
`n`	`sequence_length`	序列长度
`d`	`d_model` 或 `hidden_size`	模型/嵌入维度
`h`	`num_heads`	注意力头的数量
`k`	`head_dim`	每个注意力头的维度

其中，各维度需满足关系：d = h * k。

3. 计算流程详解

假设初始输入张量 x 的形状为 (b, n, d)。

第 1 步：线性投影 (Linear Projection)

目的 : 从输入 x 中生成 Query (Q), Key (K), Value (V) 三个向量。这三个向量分别用于匹配查询、被匹配和提取信息。

操作:

输入张量 x 分别通过三个独立的全连接层（权重矩阵为 Wq,Wk,Wv）进行线性变换。在实际高效的实现中，通常会将这三个权重矩阵融合成一个大的权重矩阵 [d, 3*d]，进行一次计算后再切分。

张量形状变化:

x: (b, n, d) -> Q, K, V: (b, n, d)

Python 复制代码

# W_q, W_k, W_v 分别是 nn.Linear(d, d)
Q = self.W_q(x)
K = self.W_k(x)
V = self.W_v(x)

第 2 步：分头 (Split Heads)

目的 : 将 d 维的 Q, K, V 向量拆分成 h 个 k 维的向量，为并行计算每个头的注意力做准备。

操作:

对 Q, K, V 进行 reshape 和 transpose 操作，将头的维度 h 提前，使其成为批处理维度的一部分。

张量形状变化:

Q, K, V: (b, n, d) -> (b, n, h, k) -> (b, h, n, k)

Python 复制代码

Q = Q.view(b, n, h, k).transpose(1, 2)
K = K.view(b, n, h, k).transpose(1, 2)
V = V.view(b, n, h, k).transpose(1, 2)

第 3 步：计算注意力得分 (Scaled Dot-Product Attention)

目的: 计算每个查询（Query）与所有键（Key）之间的相似度得分，以决定在生成输出时应该对哪些部分投入更多关注。

操作:

矩阵乘法 : 使用 torch.matmul (@) 计算 Q 和 K 的点积。注意，K 需要进行最后两个维度的转置。
缩放 (Scaling) : 将点积结果除以一个缩放因子 <math xmlns="http://www.w3.org/1998/Math/MathML"> k \sqrt{k} </math>k ，以防止梯度在 Softmax 函数中变得过小，从而稳定训练。
掩码 (Masking, 可选) : 应用掩码（如 padding mask 或 causal mask），将不需要关注的位置（例如 padding 或未来的词元）的得分设置为一个极大的负数（如 -1e9）。
Softmax : 沿最后一个维度（dim=-1）应用 Softmax 函数，将得分转换为总和为 1 的注意力权重。

张量形状变化:

Q: (b, h, n, k) 与 K.T: (b, h, k, n) -> scores: (b, h, n, n)

scores: (b, h, n, n) -> weights: (b, h, n, n)

Python 复制代码

# 1. 矩阵乘法
scores = torch.matmul(Q, K.transpose(-2, -1))

# 2. 缩放
scores = scores / (k ** 0.5)

# 3. 掩码 (可选)
# if mask is not None:
#     scores = scores.masked_fill(mask == 0, -1e9)

# 4. Softmax
atten_weights = torch.softmax(scores, dim=-1)

第 4 步：加权求和 (Weighted Sum of Values)

目的: 使用上一步计算出的注意力权重，对 Value 向量进行加权求和，得到每个头输出的上下文向量。

操作:

将注意力权重矩阵 atten_weights 与 Value 向量 V 进行矩阵乘法。

张量形状变化:

weights: (b, h, n, n) 与 V: (b, h, n, k) -> output: (b, h, n, k)

Python 复制代码

output = torch.matmul(atten_weights, V)

第 5 步：合并头并最终投影 (Concatenate Heads & Final Projection)

目的: 将所有头的输出结果拼接起来，并通过一个最终的线性层进行整合，得到多头注意力的最终输出。

操作:

转置与重塑 : 将 output 的 h 和 n 维度换回，然后通过 reshape 操作将 h 和 k 维度合并成 d，恢复原始的序列表示形状。
最终投影 : 将合并后的张量通过一个最终的全连接层（权重为 <math xmlns="http://www.w3.org/1998/Math/MathML"> W o W_o </math>Wo）。

张量形状变化:

output: (b, h, n, k) -> (b, n, h, k) -> (b, n, d)

concat_output: (b, n, d) -> final_output: (b, n, d)

伪代码:

Python 复制代码

# 1. 转置与重塑
output = output.transpose(1, 2).contiguous().view(b, n, d)

# 2. 最终投影
final_output = self.W_o(output)

4. 完整的多头自注意力机制 PyTorch 实现示例

python 复制代码

# -*- coding: utf-8 -*-
"""
完整的多头自注意力机制 PyTorch 实现示例
版本: 1.0
最后更新: 2025年10月17日
"""

import torch
import torch.nn as nn
import math

class MultiHeadAttention(nn.Module):
    """
    多头自注意力机制的完整实现
    
    该模块接收 Query, Key, Value 张量，并通过多头注意力机制计算输出。
    """
    def __init__(self, d_model: int, num_heads: int):
        """
        初始化函数
        
        参数:
            d_model (int): 模型的总维度，必须能被 num_heads 整除。
            num_heads (int): 注意力头的数量。
        """
        super().__init__()
        
        # 确保 d_model 可以被 num_heads 整除
        assert d_model % num_heads == 0, "d_model 必须能被 num_heads 整除"
        
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads # 每个头的维度 k
        
        # 定义 Q, K, V 的线性投影层
        # 这里使用独立的线性层，便于理解。在实践中，可以融合成一个大的线性层以提高效率。
        self.w_q = nn.Linear(d_model, d_model)
        self.w_k = nn.Linear(d_model, d_model)
        self.w_v = nn.Linear(d_model, d_model)
        
        # 最后的输出线性层
        self.w_o = nn.Linear(d_model, d_model)
        
    def forward(self, q: torch.Tensor, k: torch.Tensor, v: torch.Tensor, mask: torch.Tensor = None):
        """
        前向传播函数
        
        参数:
            q (torch.Tensor): Query 张量，形状为 (b, n_q, d_model)
            k (torch.Tensor): Key 张量，形状为 (b, n_k, d_model)
            v (torch.Tensor): Value 张量，形状为 (b, n_v, d_model)
            mask (torch.Tensor, optional): 掩码张量，用于屏蔽某些位置的注意力。
                                           形状可以是 (b, 1, 1, n_k) 或 (b, 1, n_q, n_k)。
                                           
        返回:
            torch.Tensor: 注意力机制的输出，形状为 (b, n_q, d_model)
        """
        b, n_q, _ = q.shape
        b, n_k, _ = k.shape
        b, n_v, _ = v.shape

        # 1. 线性投影 (Linear Projection)
        # (b, n, d) -> (b, n, d)
        q_proj = self.w_q(q)
        k_proj = self.w_k(k)
        v_proj = self.w_v(v)

        # 2. 分头 (Split Heads)
        # (b, n, d) -> (b, n, h, k) -> (b, h, n, k)
        q_heads = q_proj.view(b, n_q, self.num_heads, self.head_dim).transpose(1, 2)
        k_heads = k_proj.view(b, n_k, self.num_heads, self.head_dim).transpose(1, 2)
        v_heads = v_proj.view(b, n_v, self.num_heads, self.head_dim).transpose(1, 2)
        
        # 3. 计算注意力得分 (Scaled Dot-Product Attention)
        # (b, h, n_q, k) @ (b, h, k, n_k) -> (b, h, n_q, n_k)
        scores = torch.matmul(q_heads, k_heads.transpose(-2, -1))
        
        # 缩放
        scores = scores / math.sqrt(self.head_dim)
        
        # 应用掩码 (可选)
        if mask is not None:
            scores = scores.masked_fill(mask == 0, -1e9)
            
        # Softmax
        attn_weights = torch.softmax(scores, dim=-1)
        
        # 4. 加权求和 (Weighted Sum of Values)
        # (b, h, n_q, n_k) @ (b, h, n_v, k) -> (b, h, n_q, k)  (注意: n_k == n_v)
        output = torch.matmul(attn_weights, v_heads)
        
        # 5. 合并头并最终投影 (Concatenate Heads & Final Projection)
        # (b, h, n_q, k) -> (b, n_q, h, k) -> (b, n_q, d)
        output = output.transpose(1, 2).contiguous().view(b, n_q, self.d_model)
        
        # (b, n_q, d) -> (b, n_q, d)
        final_output = self.w_o(output)
        
        return final_output

# --- 示例用法 ---
if __name__ == "__main__":
    
    # 定义模型超参数
    d_model = 512       # 模型维度
    num_heads = 8       # 注意力头数
    batch_size = 4      # 批次大小
    seq_length = 10     # 序列长度
    
    print(f"模型维度 d_model: {d_model}, 注意力头数 num_heads: {num_heads}\n")

    # 实例化模型
    attention_module = MultiHeadAttention(d_model, num_heads)
    
    # 创建一个随机输入张量作为示例
    # 在自注意力中, q, k, v 是同一个输入
    x = torch.randn(batch_size, seq_length, d_model)
    
    # --- 场景1: 无掩码的自注意力 ---
    print("--- 场景1: 无掩码的自注意力 ---")
    output = attention_module(q=x, k=x, v=x, mask=None)
    
    print(f"输入张量形状 (x): {x.shape}")
    print(f"输出张量形状: {output.shape}")
    assert output.shape == x.shape
    print("✅ 输出形状与输入形状一致，测试通过！\n")
    
    # --- 场景2: 带因果掩码（Causal Mask）的自注意力 ---
    # 这在像 GPT 这样的解码器模型中很常见，用于防止模型看到未来的词元。
    print("--- 场景2: 带因果掩码的自注意力 ---")
    
    # 创建一个上三角矩阵作为掩码
    # torch.triu 返回矩阵的上三角部分，其余部分为0
    causal_mask = torch.triu(torch.ones(seq_length, seq_length), diagonal=1).bool()
    # 将其形状调整为 (b, 1, n, n) 以便与 (b, h, n, n) 的 scores 张量进行广播
    causal_mask = causal_mask.unsqueeze(0).unsqueeze(0) # -> (1, 1, seq_length, seq_length)
    
    # 在这个掩码中, True 代表需要被屏蔽的位置, 我们需要反转它
    # masked_fill 的逻辑是 mask 中为 True 的地方被填充
    # 我们希望未来的位置被填充，所以不需要反转
    # (更正逻辑：softmax 前，我们希望 mask=1 的位置是-inf，所以mask==True的地方填充)
    # 我们希望上三角（未来的位置）为0，其余为1
    causal_mask = ~torch.triu(torch.ones(seq_length, seq_length), diagonal=1).bool()
    causal_mask = causal_mask.unsqueeze(0).unsqueeze(0)

    # 在这个版本中，我们假设 mask 中 0 代表要屏蔽的位置
    final_causal_mask = torch.tril(torch.ones(seq_length, seq_length)).unsqueeze(0).unsqueeze(0) # (1, 1, 10, 10)

    output_masked = attention_module(q=x, k=x, v=x, mask=final_causal_mask)
    
    print(f"输入张量形状 (x): {x.shape}")
    print(f"因果掩码形状: {final_causal_mask.shape}")
    print(f"带掩码的输出张量形状: {output_masked.shape}")
    assert output_masked.shape == x.shape
    print("✅ 带掩码的输出形状正确，测试通过！")

5. 总结

多头自注意力机制通过**"投影 -> 分头 -> 并行计算注意力 -> 合并 -> 再投影"** 的优雅流程，极大地增强了模型捕捉长距离依赖和复杂上下文信息的能力。其核心在于利用 torch.matmul (@) 对最后两个维度进行矩阵乘法，同时将前面的维度作为批处理维度，从而高效地并行处理多个头的计算。