「用Python来学微积分」5. 曲线的极坐标方程

一、作极坐标方程表示的曲线

1. 作 pcos⁡θ=2p\cos \theta = 2pcosθ=2 所代表的曲线

Python代码:

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from test_4_00 import create_polar_system

# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 圆心在(0,-a)的圆方程：ρ = -2asinθ
theta = np.linspace(0, 2*np.pi, 200)
color = 'r'
# 计算ρ值：ρ = 2/cos θ
rho_simplified = 2/ np.cos(theta)
# 绘制曲线
ax.plot(theta, rho_simplified, 'b--', linewidth=2,
        label=f'ρ = 2/cosθ')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()

执行结果:

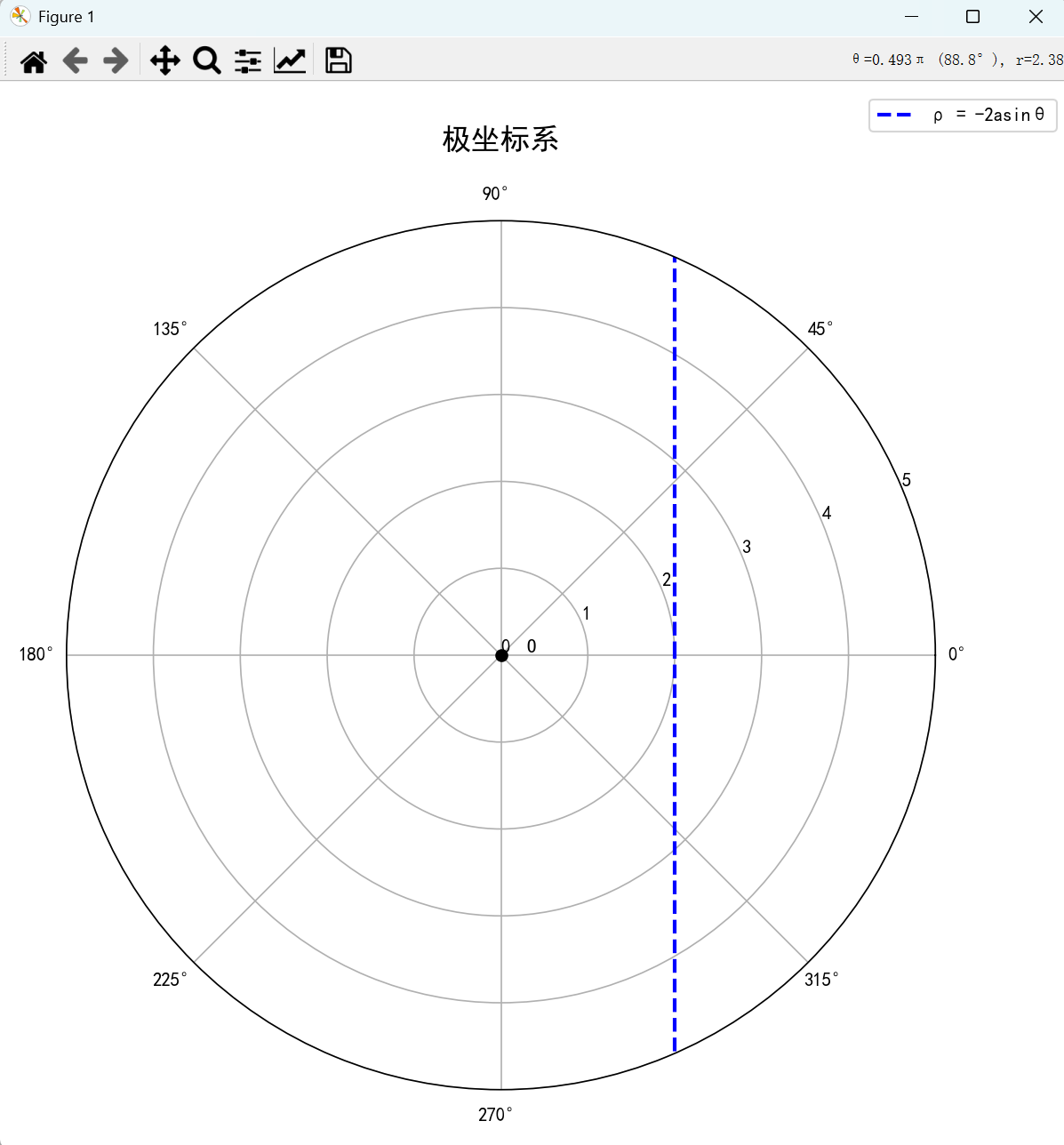
2. 作 θ=3π4\theta = \frac{3\pi}{4}θ=43π 所代表的曲线

Python方程:

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from test_4_00 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 固定的θ值
theta = 3*np.pi/4
color = 'r'
# 创建r值数组
r_values = np.linspace(0, 5, 100)
# 创建θ值数组（全部为固定值）
theta_values = np.full_like(r_values, theta)
# 绘制θ = 3π/4对应的曲线
ax.plot(theta_values, r_values, color + '-', linewidth=2.5, label='θ=3π/4')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()

运行结果:

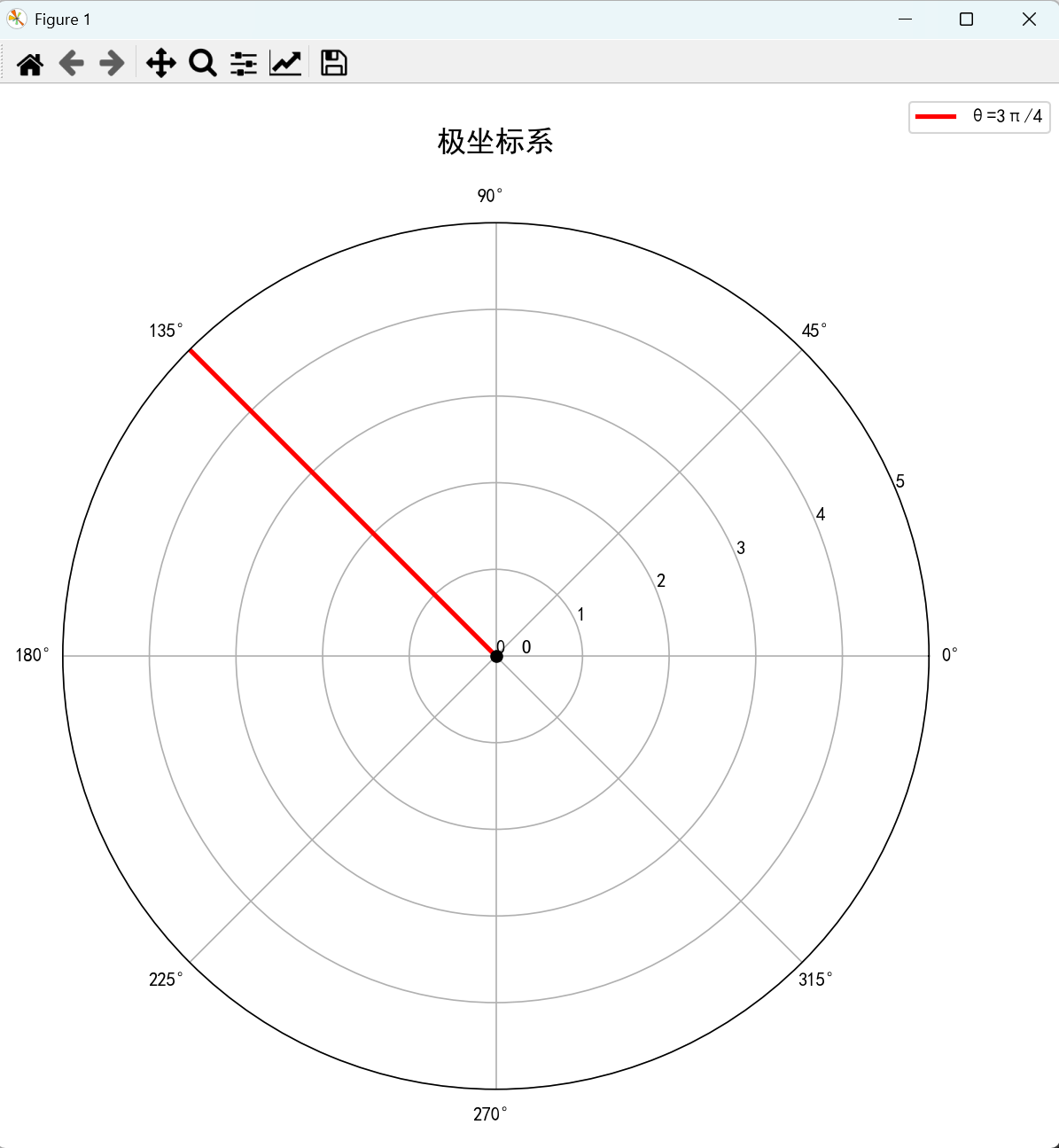
二、四类常见曲线的极坐标方程

用极坐标方程还可以表示一些在直角坐标系中较难表示的复杂的曲线

1. 阿基米德螺线

当一个动点沿着一条射线作等速运动，而射线又绕着它的端点作等速旋转时，这个动点的轨迹叫做阿基米德螺线(等速螺线)

设曲线上动点 M 的坐标(p,θ)(p, \theta)(p,θ) , 动点在初始位置M0M_0M0 的坐标为 (p0,0)(p_0, 0)(p0,0), M 在 l上运动的速度为v，l 绕O转动的角速度为w。可以得出，经过时间t， M的极径为 p=p0+vtp = p_0 + vtp=p0+vt , 极角为 θ=wt\theta = wtθ=wt . 令 a=vwa = \frac{v}{w}a=wv ,得p=p0+aθ(a,p0为常数，a≠0)p = p_0 + a\theta (a,p_0 为常数， a\neq 0)p=p0+aθ(a,p0为常数，a=0) ，这就是阿基米德螺线的曲线方程。

Python代码:

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from test_4_00 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 10))
ax.set_title('阿基米德螺线 (r = aθ)', fontsize=16, pad=20)
# 定义阿基米德螺线参数
a = 0.5  # 螺线参数
theta = np.linspace(0, 4*np.pi, 1000)  # 角度范围 0 到 4π
r = a * theta  # 阿基米德螺线方程 r = aθ
# 绘制阿基米德螺线
ax.plot(theta, r, 'b-', linewidth=2, label=f'r = {a}θ')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.2, 1.1))
# 标记一些特殊点
# 每隔π标记一个点
special_thetas = np.array([0, np.pi, 2*np.pi, 3*np.pi, 4*np.pi])
special_rs = a * special_thetas
ax.plot(special_thetas, special_rs, 'ro', markersize=6)
# 添加特殊点标签
labels = ['0', 'π', '2π', '3π', '4π']
for i, (t, r_val) in enumerate(zip(special_thetas, special_rs)):
    if t != 0:  # 不标记原点
        ax.text(t + 0.1, r_val + 0.2, labels[i], fontsize=10, color='red')
plt.tight_layout()
plt.show()

运行结果:

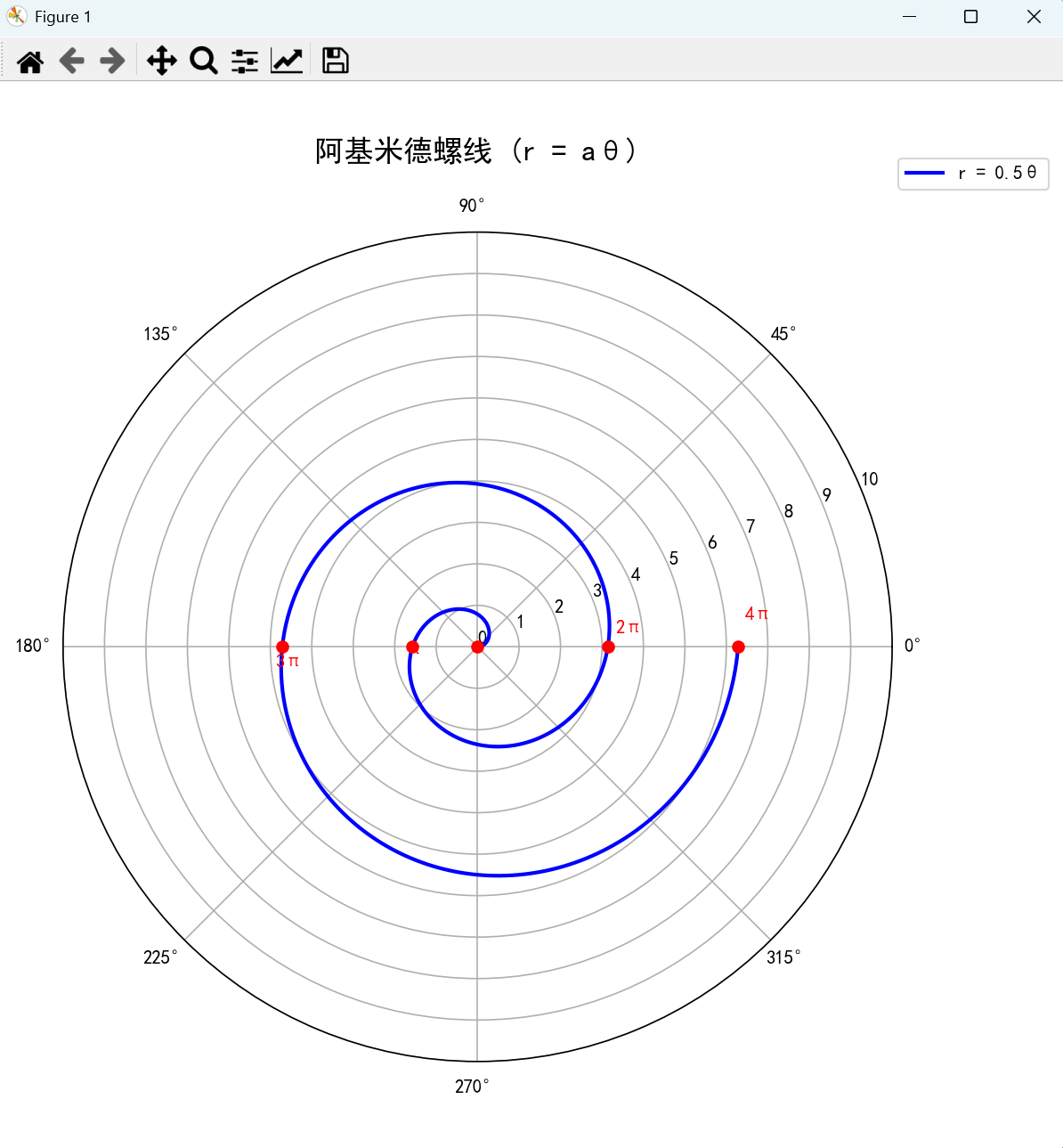
2. 心形线

设 O 为直径等于a的圆上的一点，过O点任意作直线交圆于P点。在射线 OP上取一点M，使|PM| = a。当P点在圆上移动一周时，点M的轨迹即为心形线。心形线的方程为:

p=a(1−cosθ),a>0,0<=θ<=2π p = a(1-cos\theta), a>0, 0<= \theta <= 2\pi p=a(1−cosθ),a>0,0<=θ<=2π

Python 代码:

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from test_4_00 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# θ值范围[0,2π]
theta = np.linspace(0, 2*np.pi, 200)
color = 'r'
a = 2
# 绘制圆
# 计算ρ值：ρ = -acosθ
p = -a * np.cos(theta)
ax.plot(theta, p, 'b--', linewidth=2,
        label=f'ρ = -acosθ')
# 绘制曲线
# 计算ρ值：ρ = a(1-cosθ)
p1 = a*(1-np.cos(theta))
ax.plot(theta, p1, 'b--', linewidth=2,
        label=f'ρ = a(1-cosθ)')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()

运行结果:

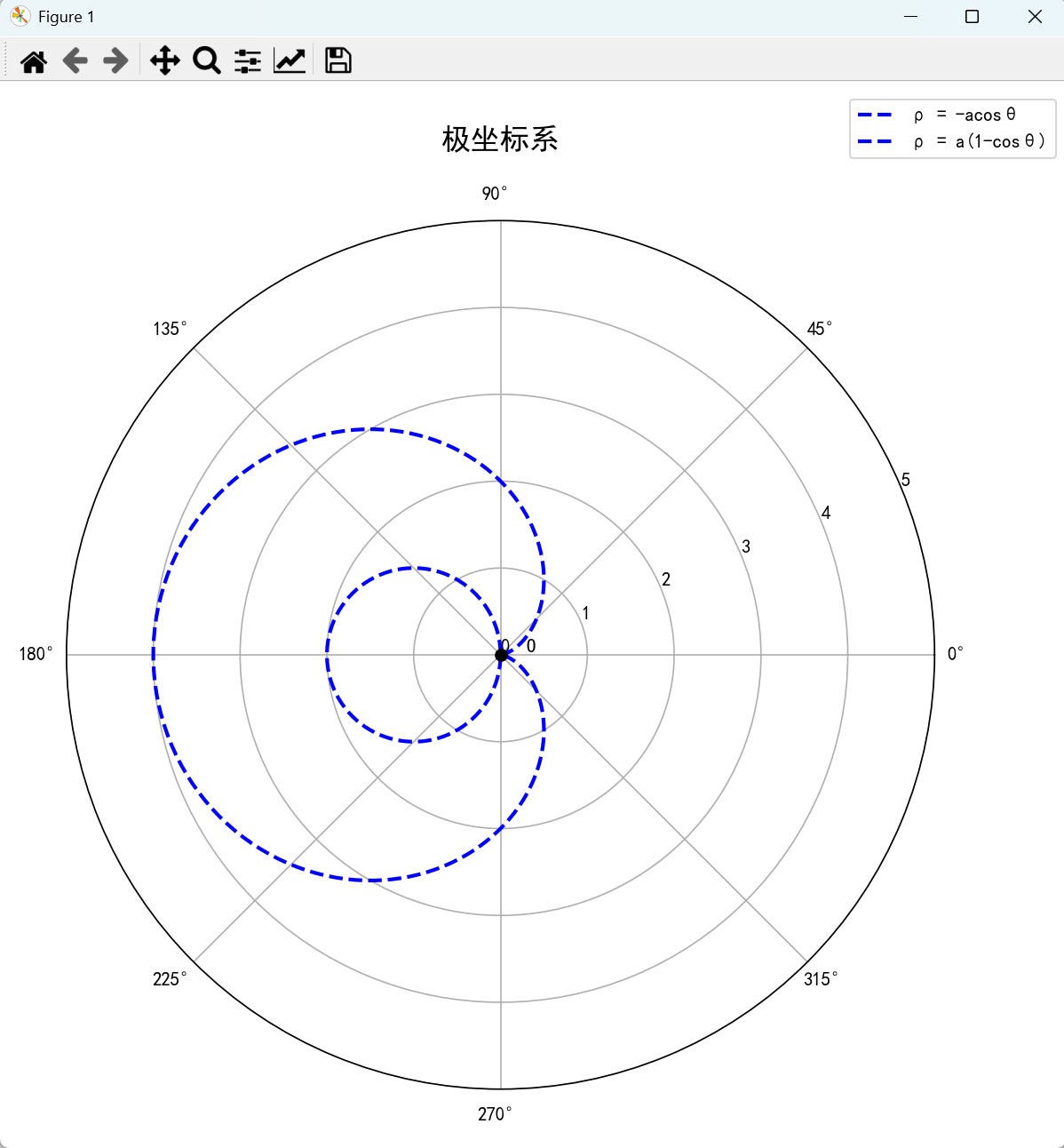
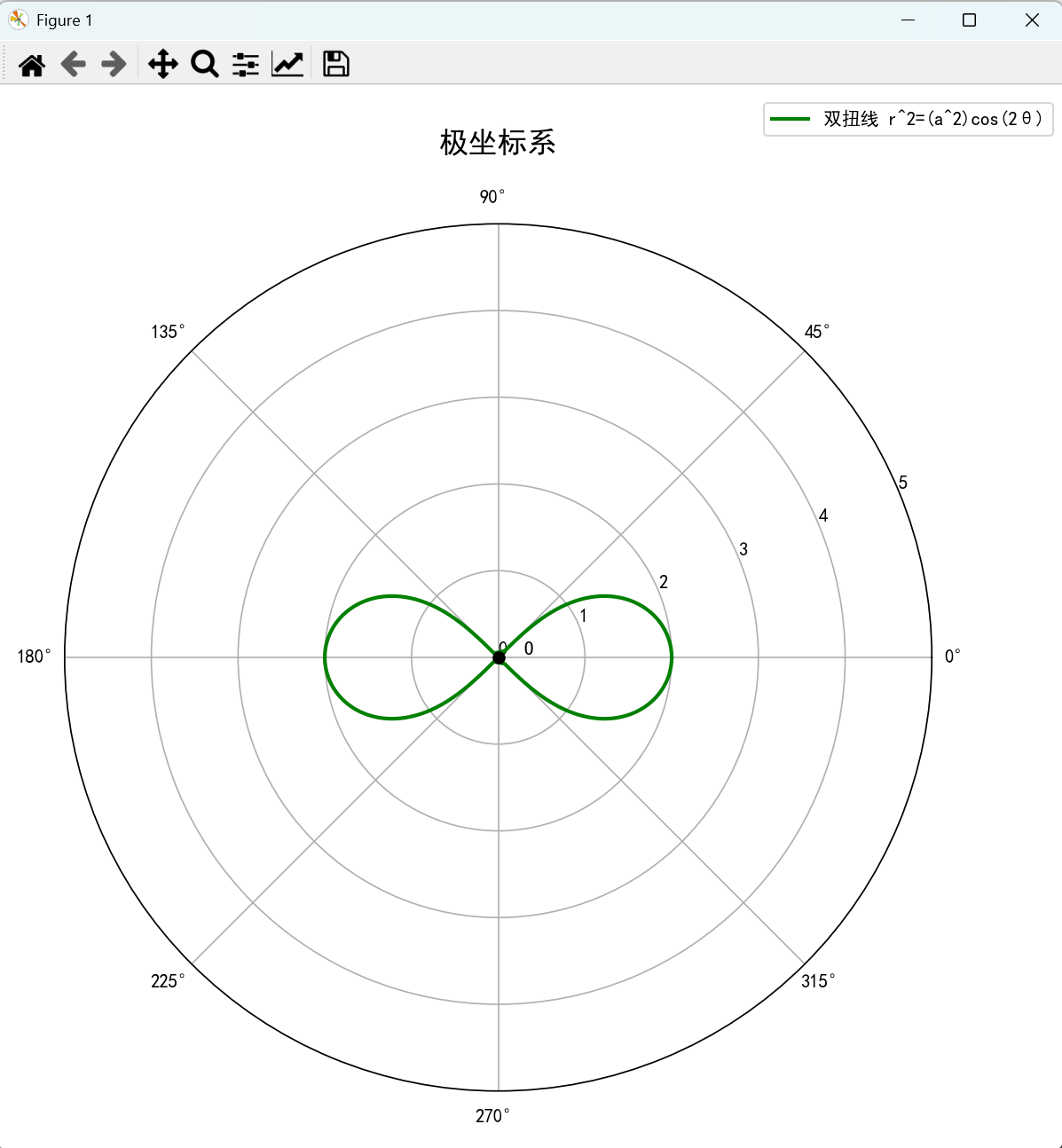
3. 双扭线

双纽线也称伯努利双纽线。设定线段AB长度为2a，动点M满足MA∗MB=a2MA*MB = a^2MA∗MB=a2, 那么M的轨迹称为双纽线。双扭线的极坐标方程为:

p2=2a2cos⁡2θ或p2=2a2sin⁡2θ p^2 = 2a^2\cos 2\theta \quad 或 \quad p^2 = 2a^2\sin 2\theta p2=2a2cos2θ或p2=2a2sin2θ

Python 代码:

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from test_4_00 import create_polar_system
# 创建极坐标系
fig, ax = create_polar_system(r_range=(0, 5))
# 绘制双扭线 r^2 = a^2 * cos(2θ)
a = 2  # 双扭线参数
# 生成角度值
theta = np.linspace(0, 2*np.pi, 4000)
# 计算半径值
# r^2 = a^2 * cos(2θ)，所以 r = ±a * sqrt(cos(2θ))
# 只有当 cos(2θ) ≥ 0 时，r 才有实数解
r_squared = a**2 * np.cos(2*theta)
valid_indices = r_squared >= 0  # 找到有效的点（cos(2θ) ≥ 0）
# 计算正负两支
r_positive = np.sqrt(r_squared[valid_indices])
r_negative = -np.sqrt(r_squared[valid_indices])
# 绘制双扭线的两支
ax.plot(theta[valid_indices], r_positive, 'g-', linewidth=2, label='双扭线 r^2=(a^2)cos(2θ)')
ax.plot(theta[valid_indices], r_negative, 'g-', linewidth=2)
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.15))
# 标记极点
ax.plot(0, 0, 'ko', markersize=6, label='极点')
ax.text(0.1, 0.3, 'O', fontsize=10, color='black')
plt.tight_layout()
plt.show()

运行结果:

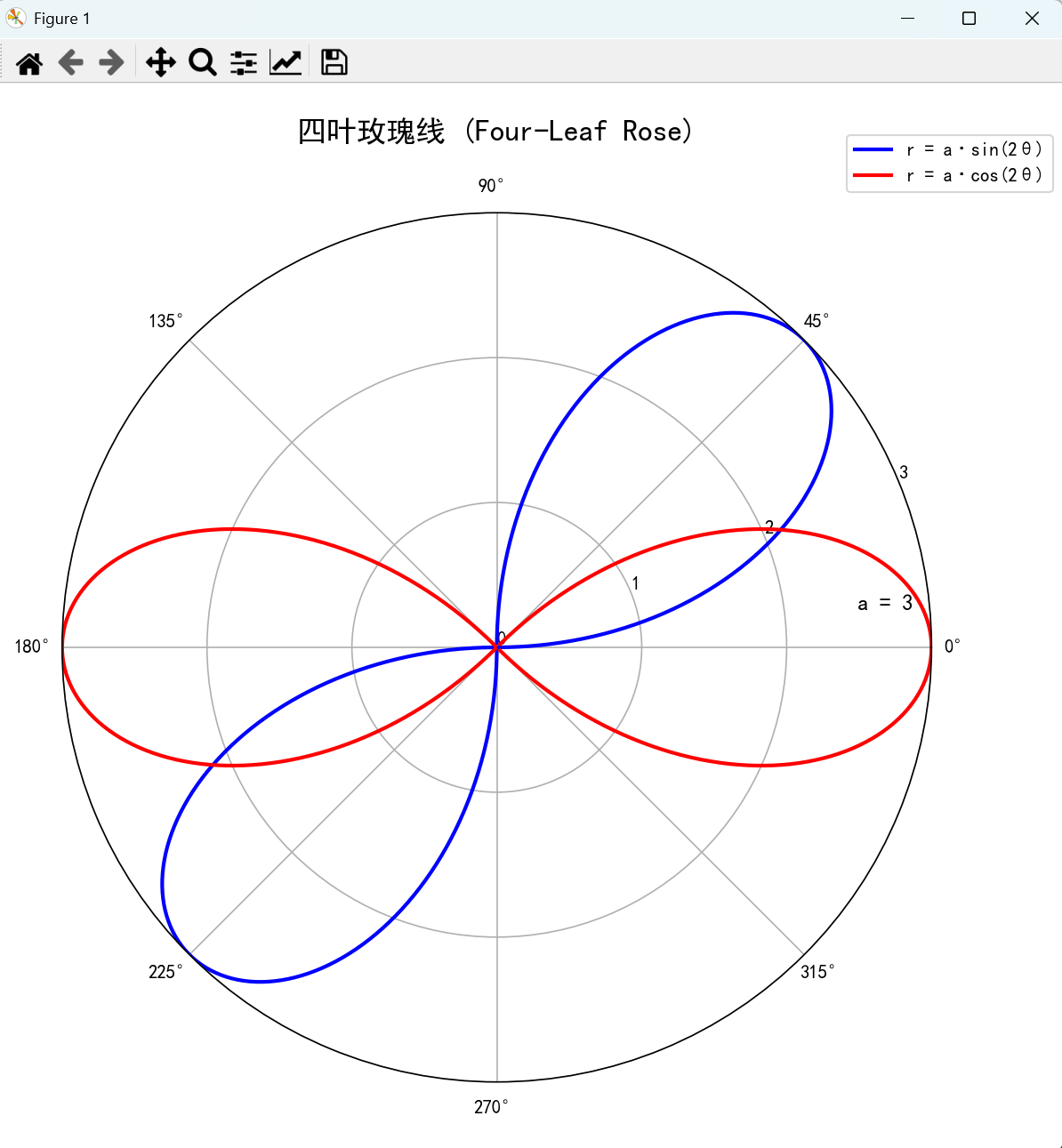
4. 四叶玫瑰线

长为2a的线段AB的两个端点 A 和 B 分别再两条相垂直的定直线上滑动，过这两条垂线的交点作点线段AB的垂线，垂足为C，称点C的轨迹是四叶玫瑰线。四叶玫瑰的极坐标方程为:

r=a∗sin⁡(2θ)或r=a∗cos⁡(2θ) r = a * \sin(2\theta) \quad 或 \quad r = a * \cos(2\theta) r=a∗sin(2θ)或r=a∗cos(2θ)

Python代码：

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from test_4_00 import create_polar_system
# 创建极坐标系（支持负半径）
fig, ax = create_polar_system(r_range=(-3, 3))
# 设置四叶玫瑰线参数
a = 3  # 控制曲线大小
# 生成角度值（密集采样确保曲线平滑）
theta = np.linspace(0, 2*np.pi, 1000)
# 计算四叶玫瑰线半径（两种常见形式）
# 形式1: r = a * sin(2θ)
r1 = a * np.sin(2*theta)
# 形式2: r = a * cos(2θ)
r2 = a * np.cos(2*theta)
# 绘制两种形式的四叶玫瑰线
ax.plot(theta, r1, 'b-', linewidth=2, label='r = a·sin(2θ)')
ax.plot(theta, r2, 'r-', linewidth=2, label='r = a·cos(2θ)')
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(1.15, 1.1))
# 添加标题
ax.set_title('四叶玫瑰线 (Four-Leaf Rose)', fontsize=16, pad=20)
# 添加参数说明
ax.text(0.1, 2.5, f'a = {a}', fontsize=12, color='black')
plt.tight_layout()
plt.show()

运行结果:

三、总结

后续我将继续使用Python实现扈志明《微积分》教材中的更多内容，包括极限、导数、积分等核心概念，通过编程实践深化对微积分知识的理解。

参考教材：扈志明，《微积分》，高等教育出版社。本文中的数学定义和概念均来源于此教材。