蒙提霍尔问题：换不换门其实是概率陷阱
蒙提霍尔问题（Monty Hall Problem）是概率论中一个经典的难题，挑战了我们对概率的直觉理解。即使很多人参与过这个问题的讨论或实验，依然容易落入常见的"概率陷阱"。在这篇文章中，我将为大家深入剖析蒙提霍尔问题的核心，并通过一些通俗易懂的方式帮助大家理解这个概率上的反直觉现象。
一、问题描述与背景
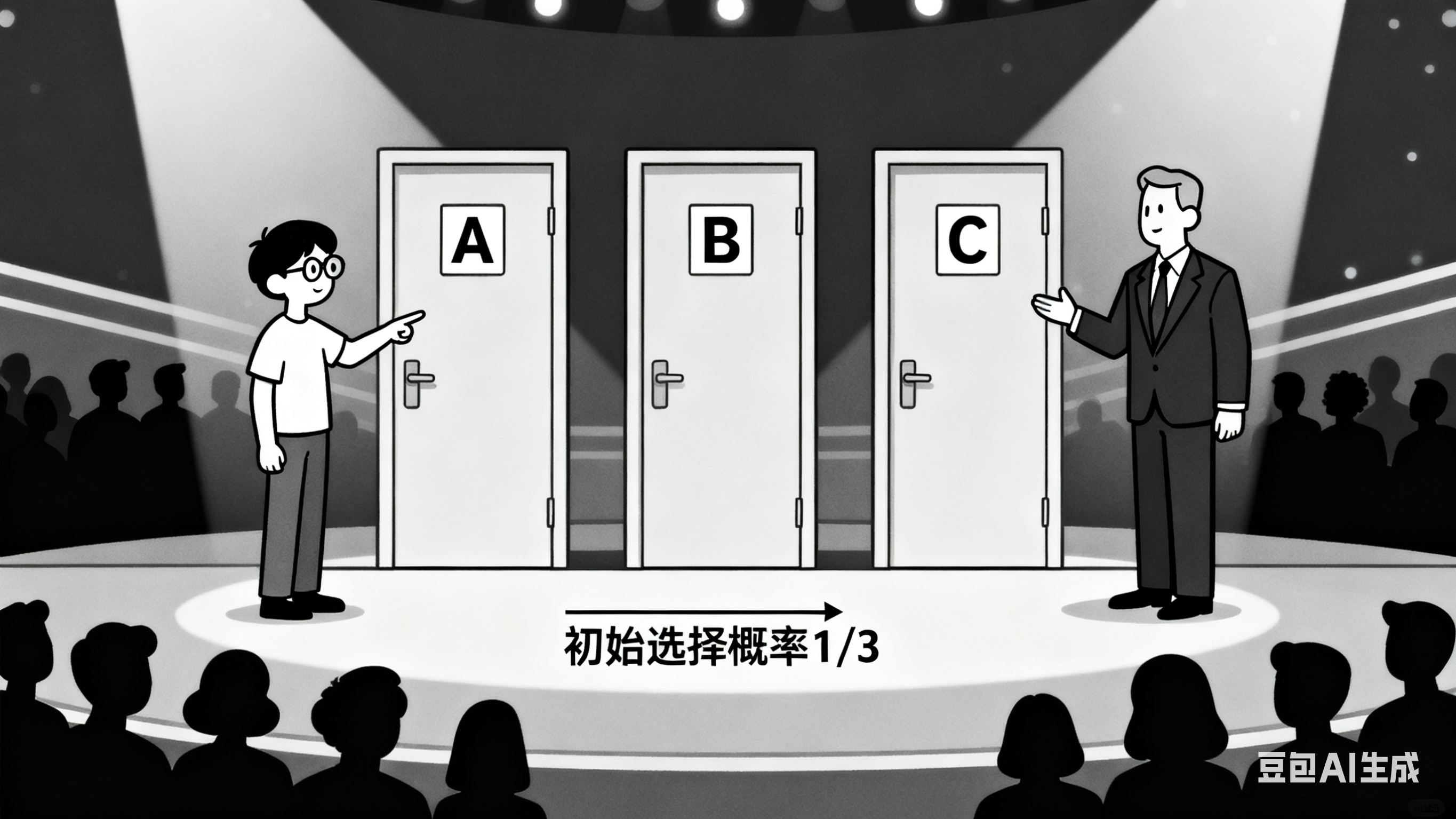
蒙提霍尔问题得名于美国著名电视节目《Let's Make a Deal》的主持人蒙提·霍尔。假设你参加了这个节目，面前有三扇门，你知道其中一扇门后藏着一辆汽车，另外两扇门后藏着的是山羊（或其他不值钱的物品）。主持人会让你先选择一扇门（假设你选了门1），然后他会打开剩下两扇门中的一扇，展示那扇门后是一只山羊。接下来，主持人问你是否要换选另一个没有被打开的门。
此时，你的直觉告诉你，既然剩下的两个门，其中一个已经被打开并展示了山羊，剩下的一扇门与最初的选择应该各有50%的概率。所以你可能会认为换门与不换的概率是相等的------但事实真的如此吗？
二、核心逻辑解析
1. 不换门（坚持初选）
假设你最初选择的是门1。无论汽车是否在门1后，主持人总是会打开一扇你没有选择的、并且后面是山羊的门。即使主持人提供了新的信息，最初选择的概率仍然是1/3。换句话说，选中汽车的概率始终为1/3。
2. 换门（改变选择）
如果你决定换门，实际情况发生了变化。当主持人打开一扇山羊门后，剩下的另一扇门背后合起来的概率已经从原来的2/3集中到了未被选中的门上。因此，换门的概率是2/3。你的新选择等于原来两个未选门的合并概率。
![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/c39e47e1f4054a9f83d888fc2f4b046e.png
3. 理解反直觉的原因
为什么这个问题如此反直觉？很多人觉得主持人的干预行为改变了游戏的"状态"，从而把它变成了一个二选一的问题。实际上，主持人并没有"重置"游戏，他的行为并没有改变你最初选择的低概率。最初的选择仅有1/3的概率会是正确的，而主持人总是会为你排除一个错误的选择，这个信息反而能帮助你提高获胜的机会。
三、用表格与枚举来理解
1. 枚举所有可能性
我们通过列举所有可能的情况，能够清晰地看到不同策略的概率分布。假设你坚持选择门1，并列出所有情况：
| 汽车位置 | 主持人打开的门 | 不换门结果 | 换门结果 |
|---|---|---|---|
| 门1 | 门2 或 门3 | 赢 | 输 |
| 门2 | 门3 | 输 | 赢 |
| 门3 | 门2 | 输 | 赢 |
从表中可以直观地看到，不换门 的获胜情况只有1种（概率为1/3），而换门的获胜情况有2种（概率为2/3）。因此，换门显然有更高的获胜概率。
2. 极端化想象
为了帮助你更好理解这个概率的反直觉现象，我们可以将这个问题从三扇门扩展到100扇门。假设你最初随机选择了一扇门（中奖概率为1%），然后主持人打开了99扇山羊门。此时，你是坚持最初选择的门（1%概率）还是换成主持人留下的那扇门（99%概率）呢？显然，在极限情况下，我们更倾向于换门，因为主持人所留下的门包含了大多数（99%）的中奖概率。
四、主持人行为对概率的影响
蒙提霍尔问题之所以有这样的反直觉效果，关键在于主持人的行为并非随机。主持人总是知道哪个门后是汽车，他打开的门不会是汽车所在的门。这一点是决定换门是否有更高获胜概率的关键。
关键变种：主持人随机开门
如果主持人不知道汽车的位置，他随机选择一扇门并打开它。这时，换与不换的概率就会变成50%：因为主持人可能会不小心打开汽车所在的门，游戏就提前结束。因此，换与不换的策略结果会趋于一致。
五、实际应用案例与启示
蒙提霍尔问题虽然是一个经典的概率谜题，但它在日常生活中也有很多应用。比如，在面对多个选择时，我们常常会因为信息不完全而做出直觉性的决策。在这种情况下，理解信息是如何逐步揭示的非常重要。蒙提霍尔问题教会我们，不能单纯地依赖我们的直觉，而应该关注主持人等关键因素所带来的信息更新。
应用实例1：股市决策
假设你决定购买一只股票，但一开始无法确定它是否会增值。你可能像蒙提霍尔问题中的参与者一样，做出了一个随机的决策。然后，一些市场信息开始显示某个股票的潜力，你面临是否继续持有或者卖出的选择。如果你只依赖初始的判断（即坚持"不换门"），你可能错失了基于新信息作出更合理决策的机会。
应用实例2：招聘面试决策
在招聘过程中，面试官的提问和后续的反馈信息会影响你对候选人的最终判断。如果最初的判断是"没有什么特别亮点"，那么通过后续的面试信息更新，你可能会发现一个潜在的人才。类似于蒙提霍尔问题，你会更倾向于"换门"，也就是更新你对候选人的评估。
六、结论与核心启示
蒙提霍尔问题的核心启示在于：在做决策时，信息的逐步揭示至关重要。主持人的"非随机"行为是影响最终决策的关键因素，它为你提供了新的信息，帮助你做出更理性的选择。在面对复杂的决策时，我们应该关注信息的更新过程，而不仅仅是直觉中的初始概率。
希望这篇文章能帮助你更好理解蒙提霍尔问题，并提醒我们在做决策时如何避免概率的"陷阱"。如果你对其他概率论中的反直觉现象感兴趣，我也很乐意继续与你探讨！