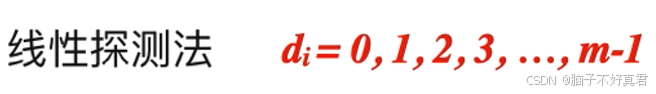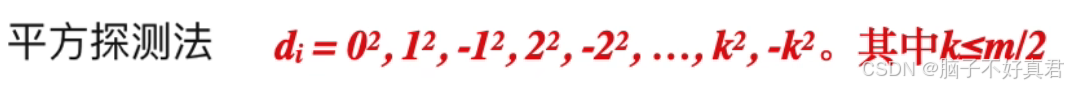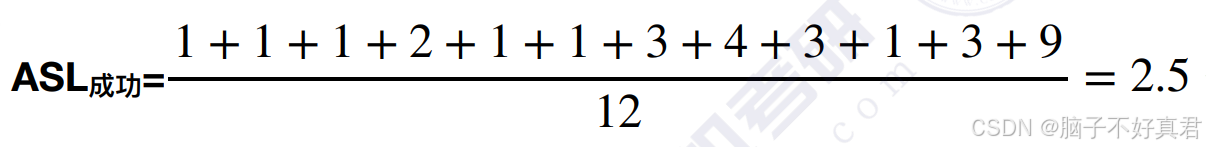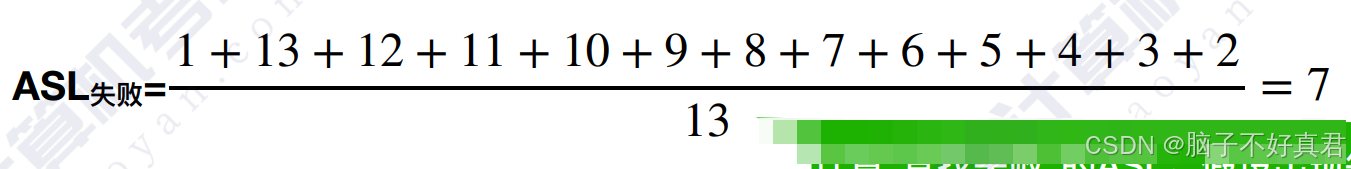查找——一文速通

脑子不好真君2025-10-22 18:13

一、掌握顺序查找算法、折半查找算法

(1)顺序查找算法

算法思想

顺序查找，又叫"线性查找"，通常用于线性表，线性表又分顺序和链式，所以顺序查找适用于顺序和链式。

核心思想：从头到尾或从尾到头遍历挨个查找。

代码

cpp 复制代码 
int SequentialSearch(int arr[], int n, int target) {
    for (int i = 0; i < n; i++) {
        if (arr[i] == target) {
            return i;  // 返回目标元素的索引
        }
    }
    return -1;  // 未找到
}

ASL分析

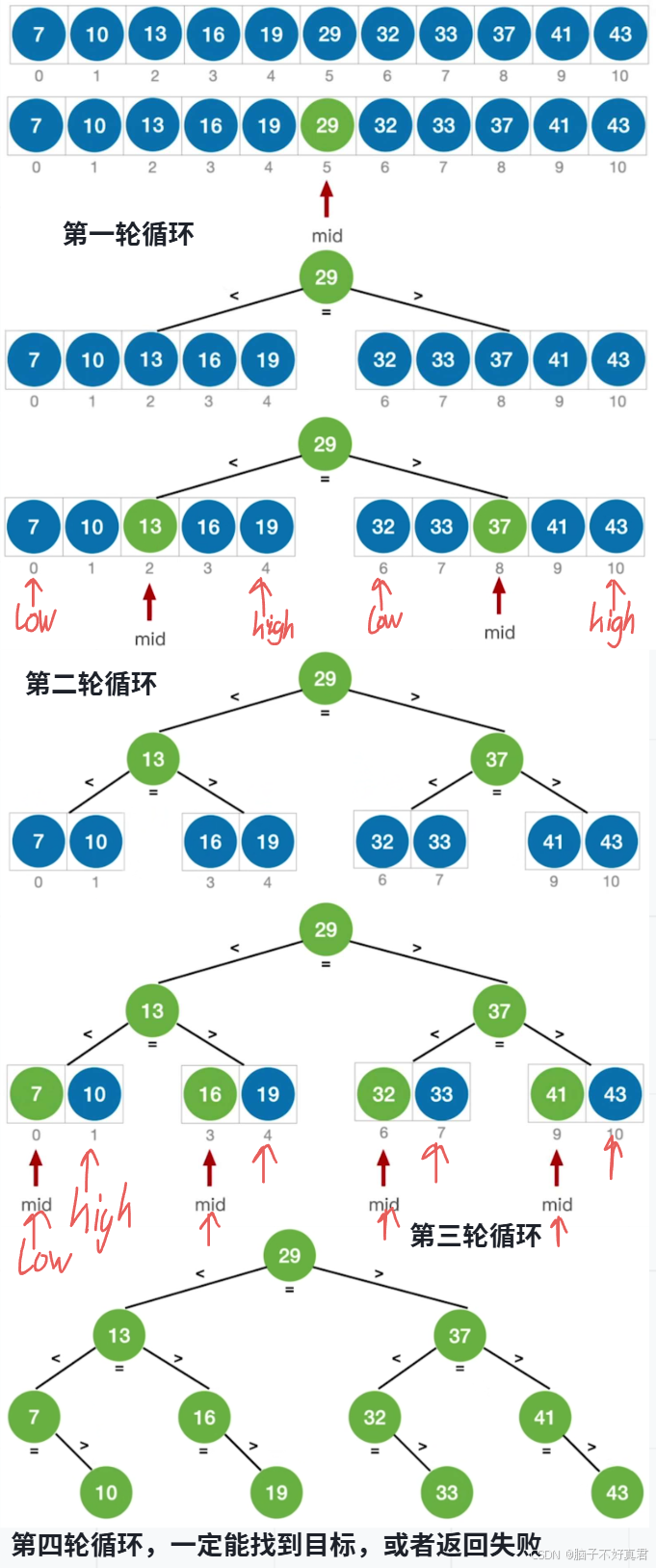
(2)折半查找算法

算法思想

折半查找（二分查找）是一种高效的查找算法，但​​仅适用于有序（元素递增或递减）数组 ​​。

核心思想是：

①​​每次比较中间元素​​，将查找范围缩小一半。

②如果目标值等于中间元素，查找成功。

③如果目标值小于中间元素，则在左半部分继续查找。

④如果目标值大于中间元素，则在右半部分继续查找。

⑤重复上述过程，直到找到目标或查找范围为空。

代码

cpp 复制代码 
int BinarySearch(int arr[], int n, int target) {
    int left = 0, right = n - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;  // 避免溢出
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            left = mid + 1;  // 目标在右半部分
        } else {
            right = mid - 1;  // 目标在左半部分
        }
    }
    return -1;  // 未找到
}

ASL分析

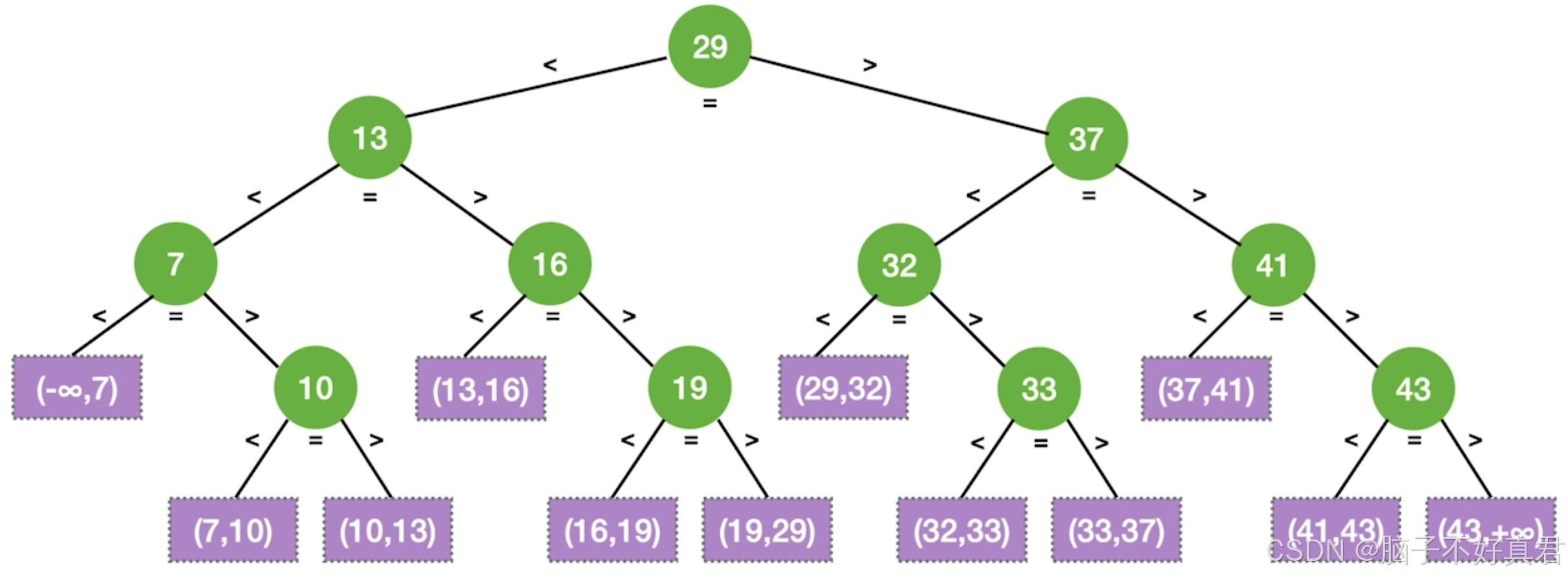
最后再标上查找失败的结果：

二、掌握二叉排序树的构造和查找算法

(1)二叉排序树的构造

二叉排序树（BST）的定义​​

二叉排序树，也称为二叉查找树，它或者是一棵空树，或者是具有以下性质的二叉树：

若它的左子树不空，则​​左子树​​上所有结点的值均​​小于​​它的根结点的值。

若它的右子树不空，则​​右子树​​上所有结点的值均​​大于​​它的根结点的值。

它的左、右子树也分别为二叉排序树。

这个定义具有​​递归性​​，它赋予了BST一个关键特性：​​中序遍历二叉排序树，可以得到一个递增的有序序列​​。

算法思想​​

若二叉树为空，则新插入的结点作为根结点。

若二叉树非空，将待插入关键字 key与根结点的关键字比较：

若 key​​小于​​根结点的值，将其插入到左子树中。

若 key​​大于​​根结点的值，将其插入到右子树中。

上述插入过程在相应的子树中​​递归​​进行，直到找到合适的位置（空位置）并插入。

代码------递归实现

cpp 复制代码 
typedef struct BSTNode {
    int key;                     // 关键字
    struct BSTNode *lchild;      // 左子树指针
    struct BSTNode *rchild;      // 右子树指针
} BSTNode, *BSTree;

// 根据数组构造BST
void Create_BST(BSTree *T, int arr[], int n) {
    *T = NULL;                       // 初始化空树
    for (int i = 0; i < n; i++) {
        BST_Insert(T, arr[i]);       // 递归插入（可替换为非递归版本）
    }
}

// 递归插入关键字
int BST_Insert(BSTree *T, int key) {
    if (*T == NULL) {            // 当前子树为空，创建新结点
        *T = (BSTNode *)malloc(sizeof(BSTNode));
        (*T)->key = key;
        (*T)->lchild = (*T)->rchild = NULL;
        return 1;                // 插入成功
    } 
    else if (key == (*T)->key) { // 关键字已存在，插入失败，因为二叉排序树不允许出现重复的关键字
        return 0;
    } 
    else if (key < (*T)->key) {  // 插入左子树
        return BST_Insert(&(*T)->lchild, key);
    } 
    else {                        // 插入右子树
        return BST_Insert(&(*T)->rchild, key);
    }
}

代码------非递归实现

cpp 复制代码 
typedef struct BSTNode {
    int key;                     // 关键字
    struct BSTNode *lchild;      // 左子树指针
    struct BSTNode *rchild;      // 右子树指针
} BSTNode, *BSTree;

// 根据数组构造BST
void Create_BST(BSTree *T, int arr[], int n) {
    *T = NULL;                       // 初始化空树
    for (int i = 0; i < n; i++) {
        BST_Insert(T, arr[i]);       // 递归插入（可替换为非递归版本）
    }
}

// 非递归插入关键字
int BST_Insert_Iter(BSTree *T, int key) {
    BSTNode *p = *T, *parent = NULL; // parent记录父结点
    
    while (p != NULL) {              // 查找插入位置
        parent = p;
        if (key == p->key) {         // 关键字已存在
            return 0;
        } 
        else if (key < p->key) {
            p = p->lchild;
        } 
        else {
            p = p->rchild;
        }
    }
    
    // 创建新结点
    BSTNode *newNode = (BSTNode *)malloc(sizeof(BSTNode));
    newNode->key = key;
    newNode->lchild = newNode->rchild = NULL;
    
    if (parent == NULL) {            // 树为空，新结点为根
        *T = newNode;
    } 
    else if (key < parent->key) {    // 插入左子树
        parent->lchild = newNode;
    } 
    else {                           // 插入右子树
        parent->rchild = newNode;
    }
    return 1;                        // 插入成功
}

查找效率分析

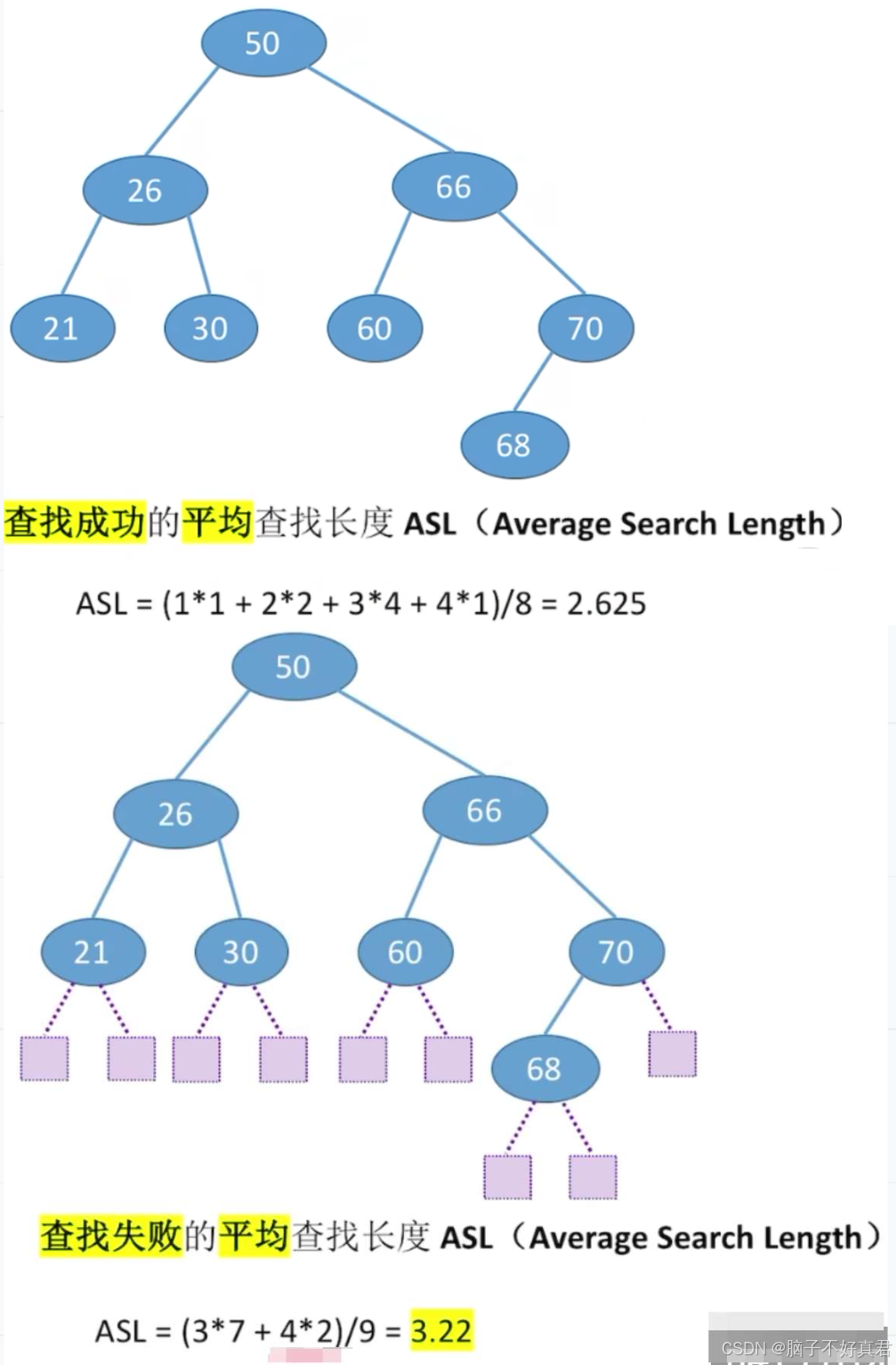
查找长度：在查找运算中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度

(2)二叉排序树的查找算法

算法思想

从根结点开始，将给定值与根结点的关键字比较：

若​​相等​​，则查找成功。

若​​小于​​根结点的关键字，则在左子树中继续查找。

若​​大于​​根结点的关键字，则在右子树中继续查找。

上述过程在相应的子树中​​递归​​进行，直到找到目标或遇到空指针（查找失败）为止。

代码------递归算法实现

cpp 复制代码 
// 二叉树结点结构
typedef struct BSTNode {
    int key; // 关键字
    struct BSTNode *lchild, *rchild; // 左右孩子指针
} BSTNode, *BSTree;

// 查找算法（递归）
BSTNode *BST_Search(BSTree T, int key) {
    if (T == NULL) { // 递归终止条件1：树空
        return T;
    }
    if (key == T->key) { // 递归终止条件2：找到目标
        return T;
    }
    if (key < T->key) {
        return BST_Search(T->lchild, key); // 在左子树中查找
    } else {
        return BST_Search(T->rchild, key); // 在右子树中查找
    }
}

代码------非递归算法实现

cpp 复制代码 
// 二叉树结点结构
typedef struct BSTNode {
    int key; // 关键字
    struct BSTNode *lchild, *rchild; // 左右孩子指针
} BSTNode, *BSTree;

// 查找算法（非递归）
BSTNode *BST_Search_Iter(BSTree T, int key) {
    while (T != NULL && key != T->key) { // 树非空且未找到目标时继续循环
        if (key < T->key) {
            T = T->lchild; // 目标值较小，转向左子树
        } else {
            T = T->rchild; // 目标值较大，转向右子树
        }
    }
    return T; // 返回找到的结点指针（若未找到则返回NULL）
}

三、掌握哈希表、哈希函数的构造方法及处理冲突的方法和平均查找长度

(0)哈希表、哈希函数、冲突和同义词的定义

哈希表、哈希函数的定义

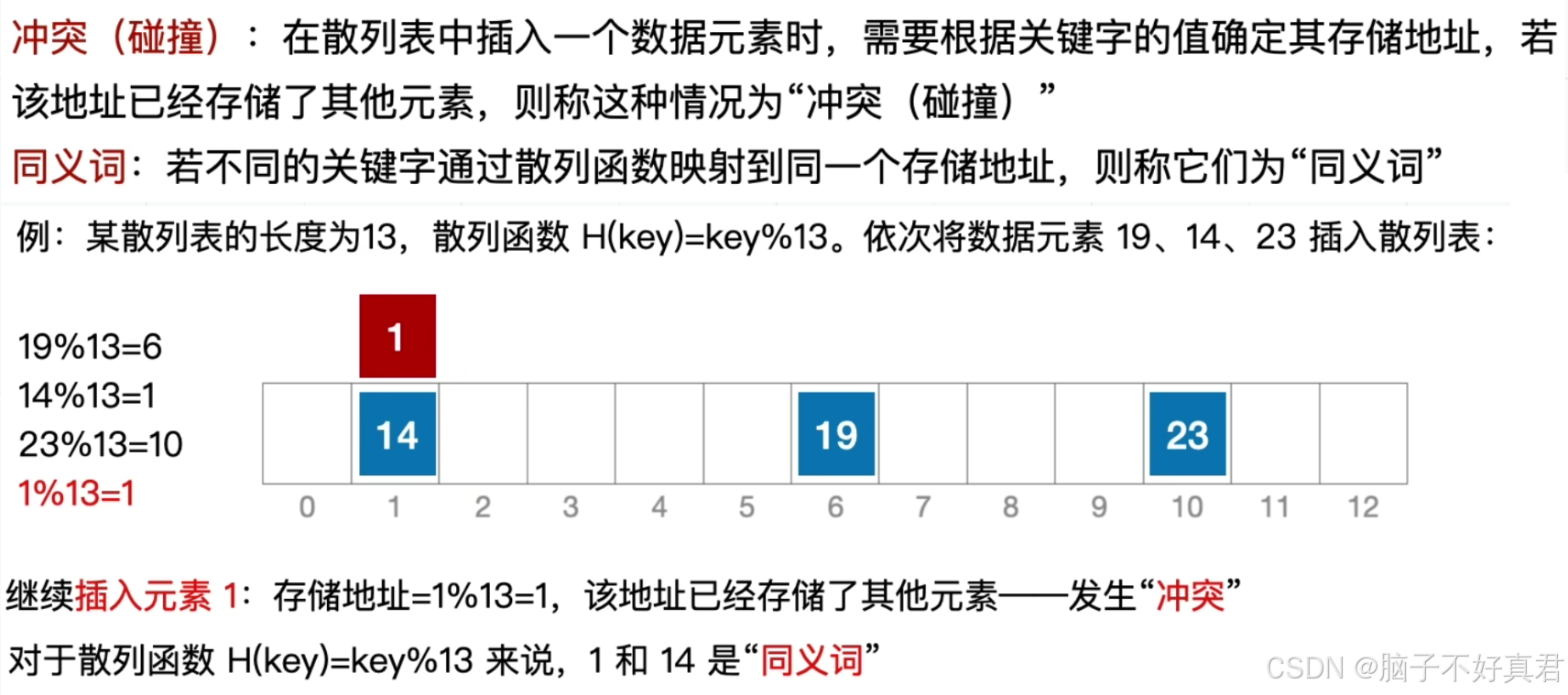
冲突、同义词的定义

(1)哈希表的构造方法

①选择一个数组作为基础存储。

②选择一个高效且分布均匀的哈希函数。

③选择一种冲突解决策略（链表法 或 开放寻址法）。

(2)哈希函数的构造方法

★除留余数法

一般形式：除留余数法-H(key)= key % p
p的选取：散列表表长为m，取一个不大于m但最接近或等于m的质数p，因为对质数取余，可以分布更均匀，从而减少冲突。

适用场景:较为通用，只要关键字是整数即可

注:质数又称素数。指除了1和此整数自身外，不能被其他自然数整除的数。

直接定址法

一般形式：直接定址法-H(key)= key 或 H(key)= a*key + b

其中，a和b是常数。这种方法计算最简单，且不会产生冲突。若关键字分布不连续，空位较多则会造成存储空间的浪费。

适用场景:关键字分布基本连续

数字分析法

平方取中法

(3)处理冲突的方法

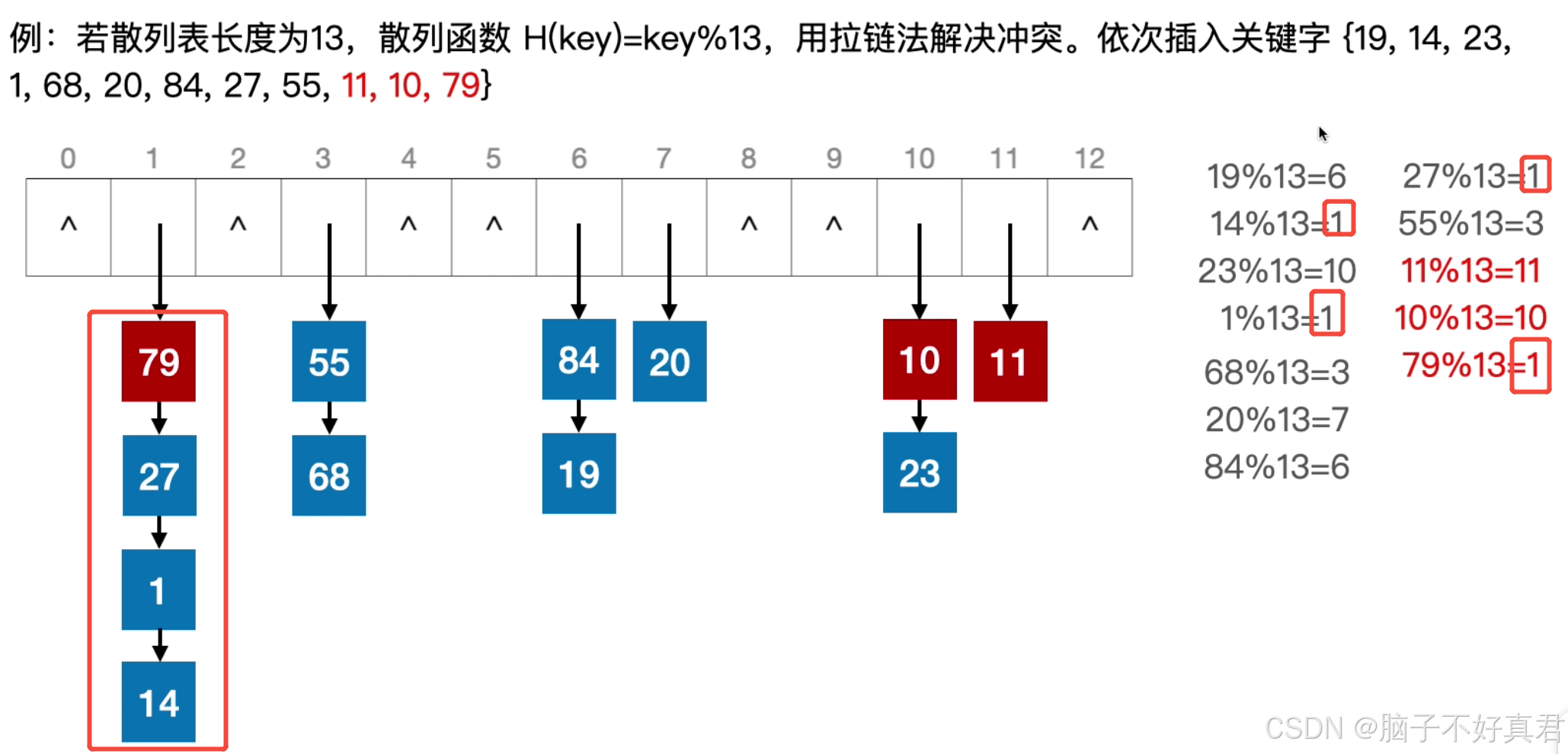
拉链法

如何在哈希表(拉链法解决冲突)中插入一个新元素?

Step 1:结合散列函数计算新元素的散列地址

Step 2:将新元素插入散列地址对应的链表(可用头插法，也可用尾插法)

核心思路：同义词挂一串

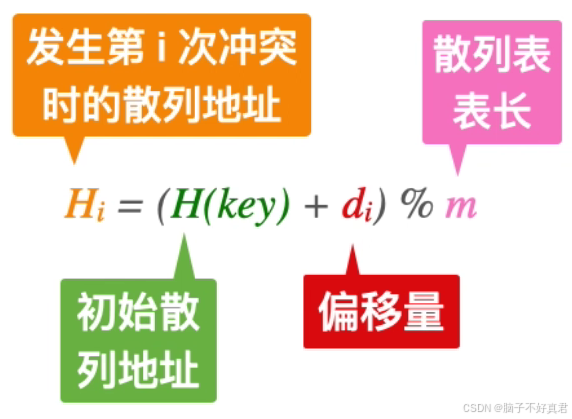
开放定址法


关键在于偏移量的设置

★十二分注意：

计算关键字的初始位置时，是与题目给出的散列函数取余，但解决冲突时是与表长取余

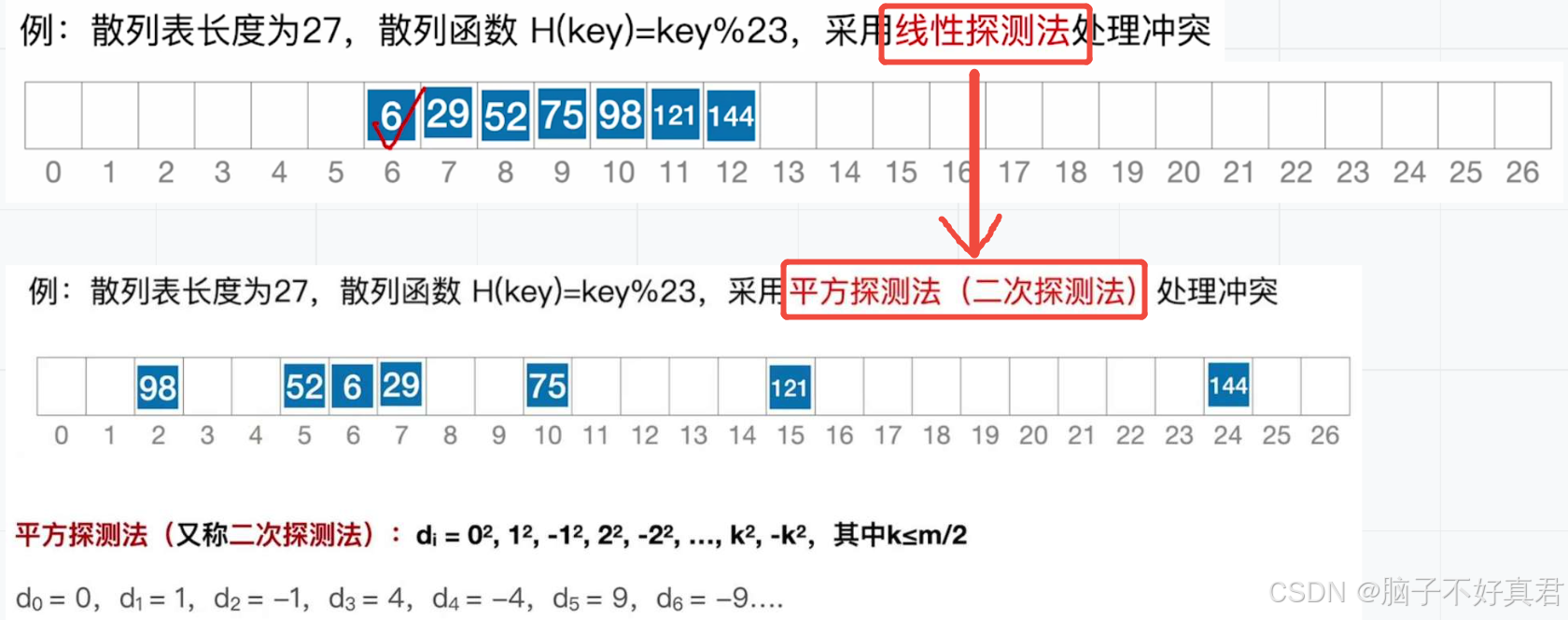
★线性探测法

偏移量：

例子：

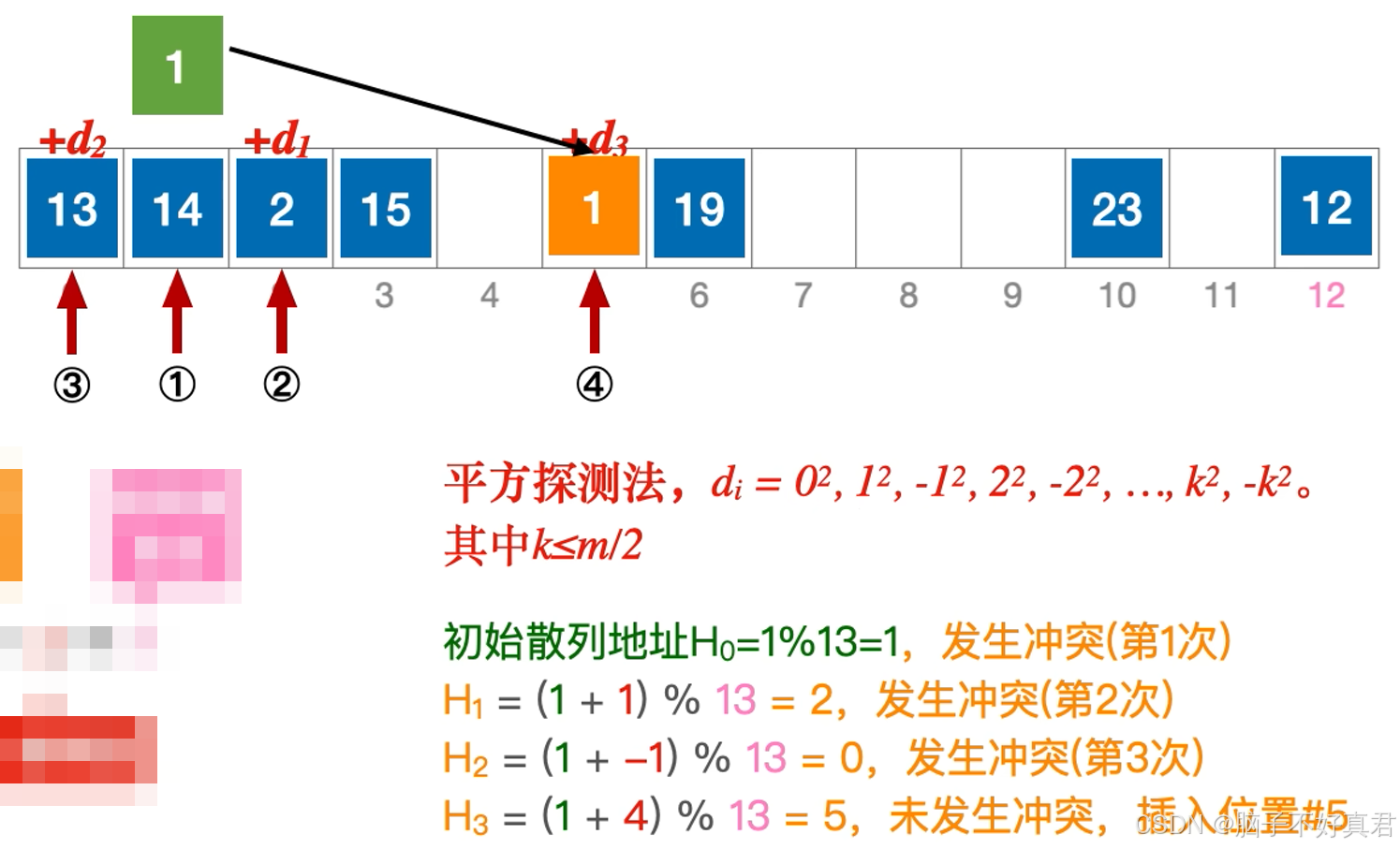
平方探测法

偏移量：

例子：

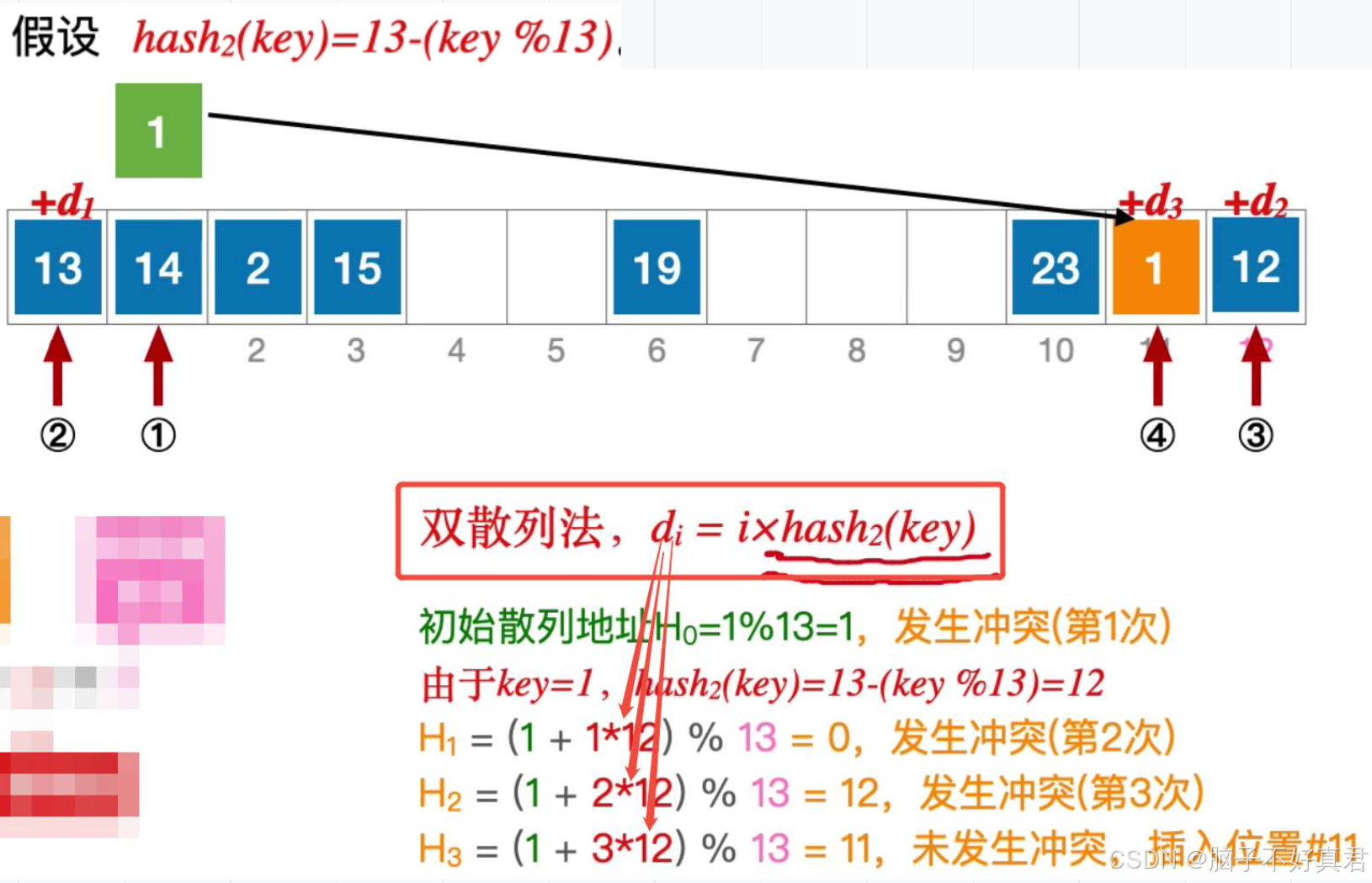
双散列法

偏移量：

例子：

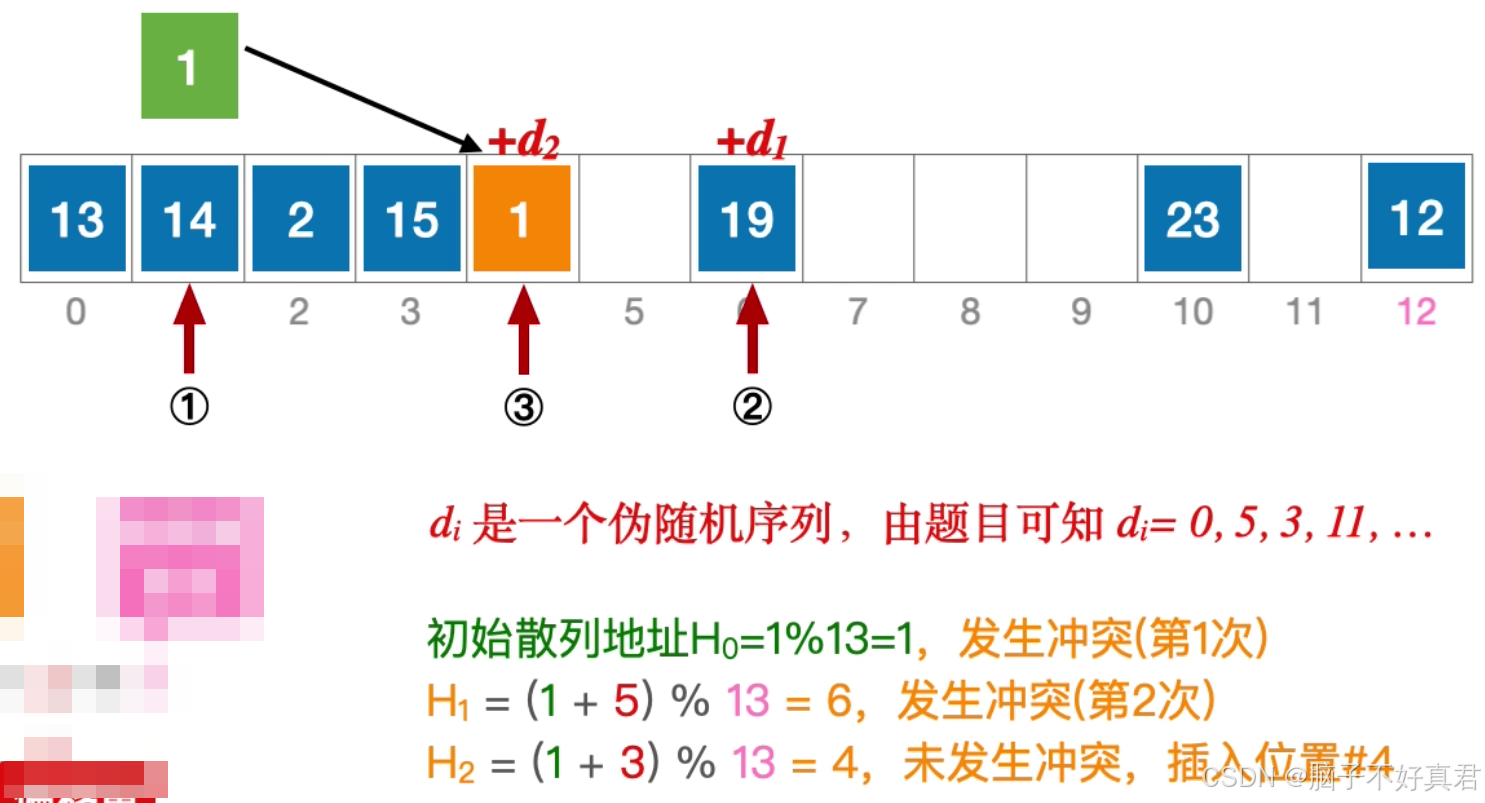
伪随机序列法

偏移量：

例子：

(4)平均查找长度

直接上例子：https://blog.csdn.net/naozibuok/article/details/152462109?spm=1001.2014.3001.5501

题目

解答

①计算出每个关键字在表中的位置
②将关键字填入表中

查找成功ASL计算


查找失败ASL计算



聚集(堆积)现象

聚集(堆积)现象:在处理冲突的过程中，几个初始散列地址不同的元素争夺同一个后继散列地址的现象称作"聚集"(或称作"堆积")

线性探测法在发生冲突时，总是往后探测相邻的后一个单元，很容易造成同义词、非同义词的"聚集(堆积)现象"，从而影响查找效率，导致ASL提升

使用"平方探测法"减少聚集现象

装填因子

热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06Labelme从安装到标注：零基础完整指南07NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南082025软件测试面试八股文（含答案+文档）09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10jdk21下载、安装（Windows、Linux、macOS）