论文阅读 - 深度学习端到端解决库存管理问题 - 有限时间范围内的多周期补货问题（Management Science）

https://pubsonline.informs.org/doi/10.1287/mnsc.2022.4564

作者：京东硅谷研究中心研究员 + 美国一些物流与供应链管理相关领域的学者。

问题：有限时间范围内的多周期库存管理问题，其中需求和供应商提前期都被认为是随机的。

目标：自动为大量库存单位输出补货决策。

效果：缩短了决策过程，显著降低了持有成本、缺货成本、总库存成本，提升库存周转率。

创新点：深度学习端到端解决库存管理问题

目录

[1. 多周期补货问题](#1. 多周期补货问题)

[1. VLT Vender Lead Time 供应商提前期](#1. VLT Vender Lead Time 供应商提前期)

[2. 问题建模 + 变量设定](#2. 问题建模 + 变量设定)

[3. 报童问题](#3. 报童问题)

[2. 相关工作](#2. 相关工作)

[1. 动态规划等传统方法](#1. 动态规划等传统方法)

[2. 两阶段 PTO 框架](#2. 两阶段 PTO 框架)

[3. E2E 模型建构](#3. E2E 模型建构)

[3.1 标注最优订货量 -- 闭式解的推导](#3.1 标注最优订货量 -- 闭式解的推导)

[3.2 神经网络结构](#3.2 神经网络结构)

[4. 实验结果](#4. 实验结果)

[4.1 和传统方法、PTO比较（理论基准）Numerical 数值实验](#4.1 和传统方法、PTO比较（理论基准）Numerical 数值实验)

[4.2 与京东当前使用的、成熟的两步PTO补货算法比较 -- Field 现场实验](#4.2 与京东当前使用的、成熟的两步PTO补货算法比较 -- Field 现场实验)

[5. 总结](#5. 总结)

---

1. 多周期补货问题

（考虑随机需求和随机供应商提前期）

1. VLT Vender Lead Time 供应商提前期

从下达补货订单到货物实际到达仓库并可用于满足需求之间所经历的时间。

"VLT问题"的本质是： 在库存管理中，供应商提前期不是固定不变的，而是不确定的、随机的。

• 如果VLT很短且确定 ，管理者可以很精确地知道何时需要下单，以应对未来的需求。

• 但现实中VLT是随机的（例如，由于运输延迟、供应商生产问题、海关延误等），这意味着你无法确切知道已下达的订单何时会到达。这可能导致：

  • 到货太晚： 如果VLT比预期长，库存可能耗尽，导致缺货和销售损失。

  • 到货太早： 如果VLT比预期短，库存会过早增加，导致持有成本上升。

2. 问题建模 + 变量设定

离散化 1-T 的时间，

• 需求： 每个时期 t 有一个随机需求 D_t 。其具体实现值记为 d_t。

• 库存水平： 每个时期初的库存水平记为 I_t。

• 持有成本： 每个期末，单位库存积压成本 h。

• 缺货成本： 每个期末，单位订单积压成本 b。

• **下单时间和数量：**第 m 个订单，在 t_m 时间点下单（提前指定），购买量为 a_m（决策）。

• VLT ：随机变量 L_m，即订单会在 t_m + L_m 到达

总结：需求和 VLT （ D_t 和 L_m ）是随机变量，a_m 为决策变量，其余已知。

库存水平更新公式：下期初库存 = 本期初库存 - 本期需求 + 本期到达的所有订单数量。

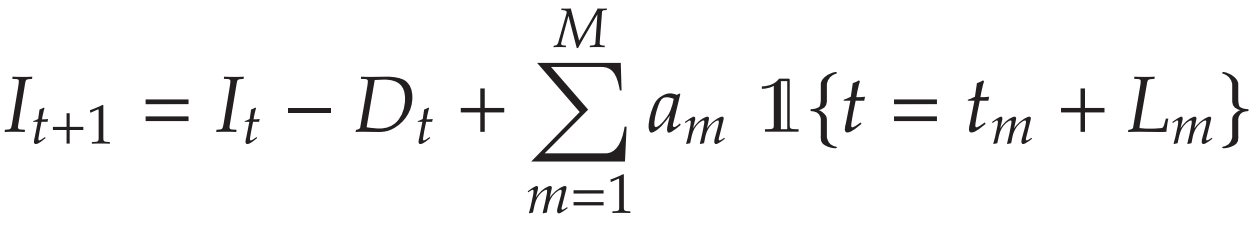
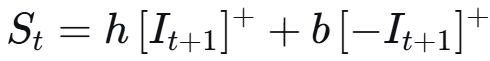
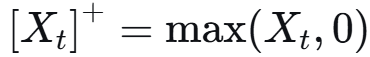
目标：找到一个最优的订购量序列 (a_1, a_2, ..., a_M)，以最小化 T 时间段的总期望成本。

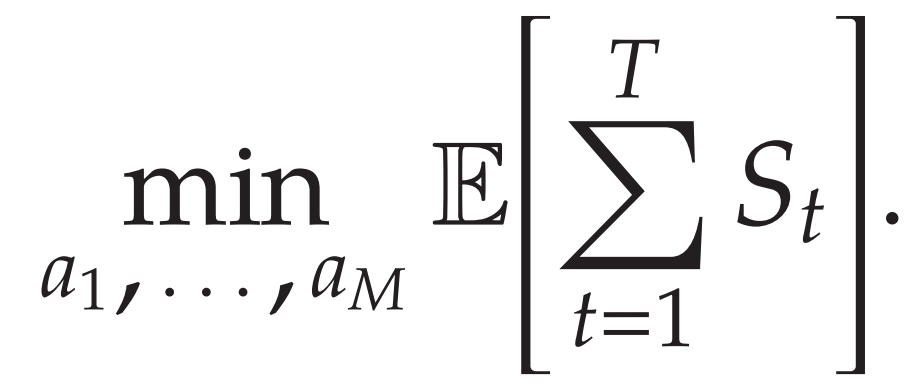期望对两个随机变量求。

3. 报童问题

单周期，随机需求 D（概率密度函数设为 f(x)），单位取货成本 b，持有成本 h。求订货量 Q*。

期望成本为：

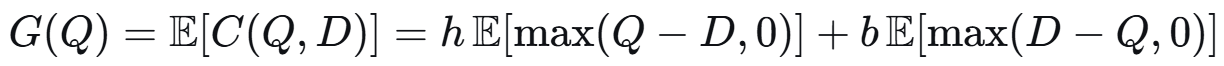
写成积分形式：

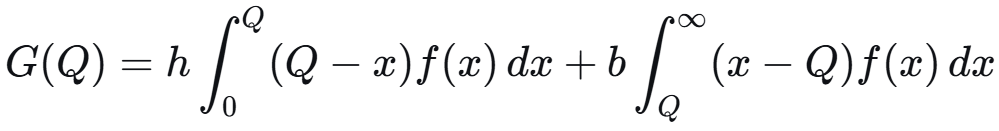
莱布尼兹法则求导：

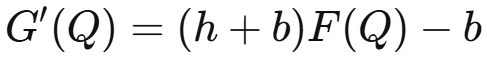
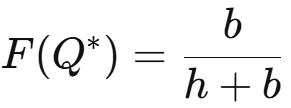
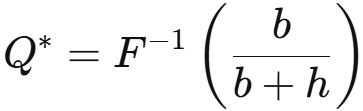
b / (b + h) 被称为关键比率，Q* = 需求分布 F 的 b / (b + h) 分位数。

多周期补货问题在两个方面与报童问题有本质区别：

1. 多周期设定，其中当前决策会影响未来，而不是报童问题中的单周期设定；

2. 除了随机需求 还有 随机 VLT供应商提前期。

2. 相关工作

1. 动态规划等传统方法

基于严格的数学模型和假设（如需求和 VLT 服从特定分布 如正态分布、伽马分布）

代表工作：基库存策略、 (s, S) 策略

最优参数难计算 -> 二倍近似算法 / 启发式算法 / 近视策略

局限性 ：假定对需求和VLT有某种了解（如遵循某些参数已知的分布模型）。

在实践中，决策者通常无法获知此类信息。

因此，两步式 PTO 框架在工业界的库存管理中被广泛采用。

2. 两阶段 PTO 框架

• 核心思想：将问题拆解为两个独立的步骤：

  1. 预测阶段：使用历史数据预测 需求和VLT。

  2. 优化阶段 ：将预测结果（点估计或分布）作为输入，代入到传统的决策规则中进行优化。

• 局限性：

  1. 信息损失 ：两阶段解耦 导致丢失信息，偏离实际带来误差。

  2. 次优性 ：预测目标和优化目标不一致，预测的"最准确"不代表能导致"最优"的决策，导致后续优化次优。

  3. 求解困难 ：即使能做出完美的分布预测，求解多周期随机动态规划 问题本身仍然计算困难。

（本文2020年6月被接受）机器学习社区近年来，基于"端到端学习"构建的系统数量急剧增加 (Donti et al. 2017)。从原始输入直接预测，而不是通过中间步骤。这一概念已成功应用于广泛的任务，例如金融 (Bengio 1997)、图像识别 (Wang et al. 2011) 和机器人操作 (Levine et al. 2016)。

本文则为应用到供应链管理问题。

3. E2E 模型建构

通过有监督学习建立一个模型（函数 f），能够根据输入的特征 x（如历史数据、时间等），直接输出最优的订货量 a。

3.1 标注最优订货量 -- 闭式解的推导

拥有完整数据后 "上帝视角"-- 反推每个订货时点的最优订货量。

第 m 个订单 在 t_m 时间下单，在 v_m 时间到达。

已知每天的需求和每个订单的到达时间（已知到达时间相当于 VLT=0）。

在 v_m 初始有 I 的库存，则后续成本递归的拆成：v_m+1 之后的成本 + [v_m,v_m+1]之间每一天的成本

（运筹学二 动态规划 从后往前推）

状态转移方程如下：

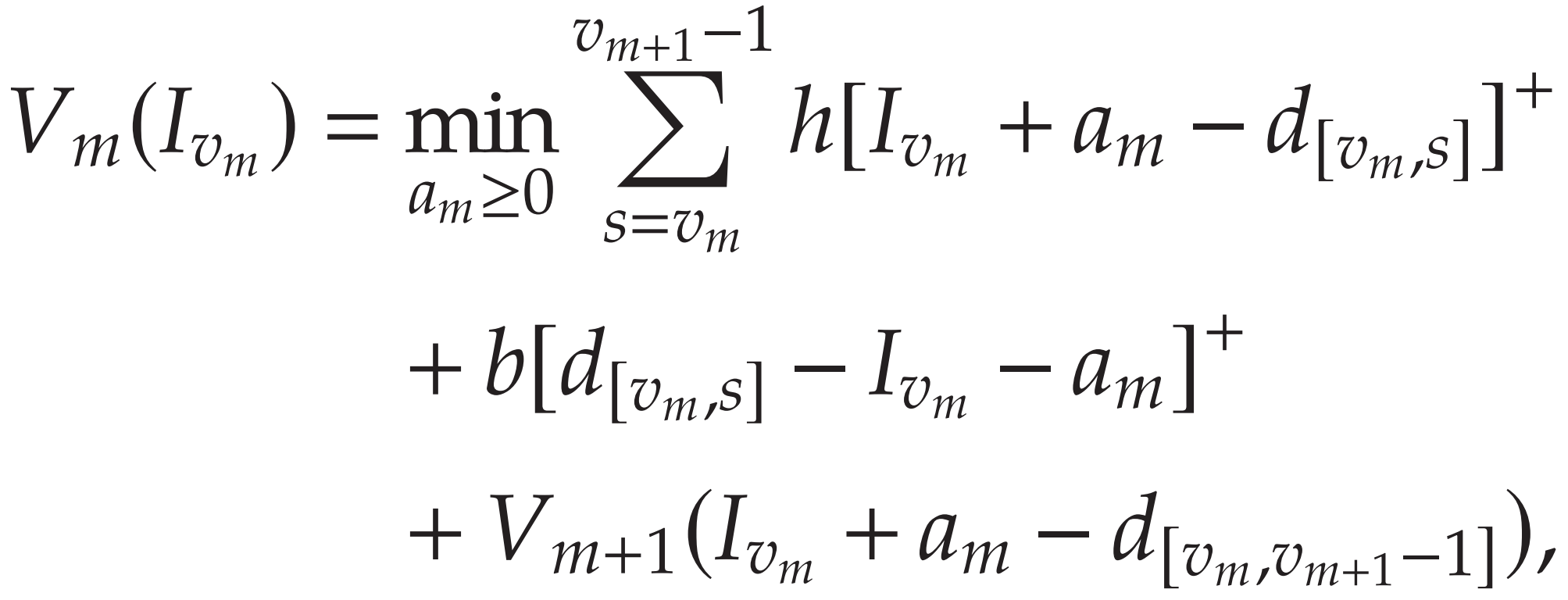
闭式解（快速标注）：

引理1：由于上一阶段只影响下一阶段的 I；不同周期之间可独立拆分；-> 转换为单周期

（可调整下一阶段的进货量，抵消掉上一阶段的调整，从后往前递推）

引理2：考虑时间区间 [t_1, t_2] 内的总库存成本

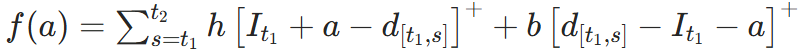
宏观来看，平衡缺货和持有成本，从缺货时点 s 之前持有，之后缺货。（每个时间段末 I<0）

由于"积压"与需求的累积 accumulate 相关，先做一个前缀和。

a的增减相当于把分界线 I+a 上下平移一个单位。 n = t2​+1−t1

a = 0，s=0 一直缺货，斜率为 -b*n；

a = ∞，s=n，斜率为 h*n。

s+1则 -> 斜率 +b+h，为 (b+h)*s-b*n

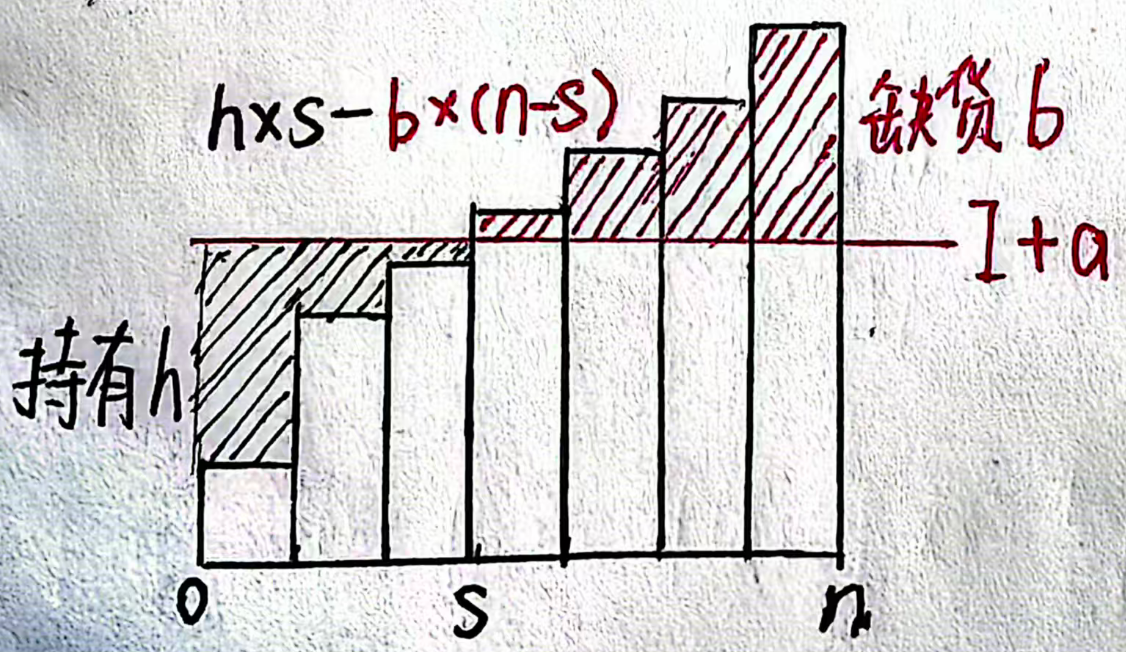
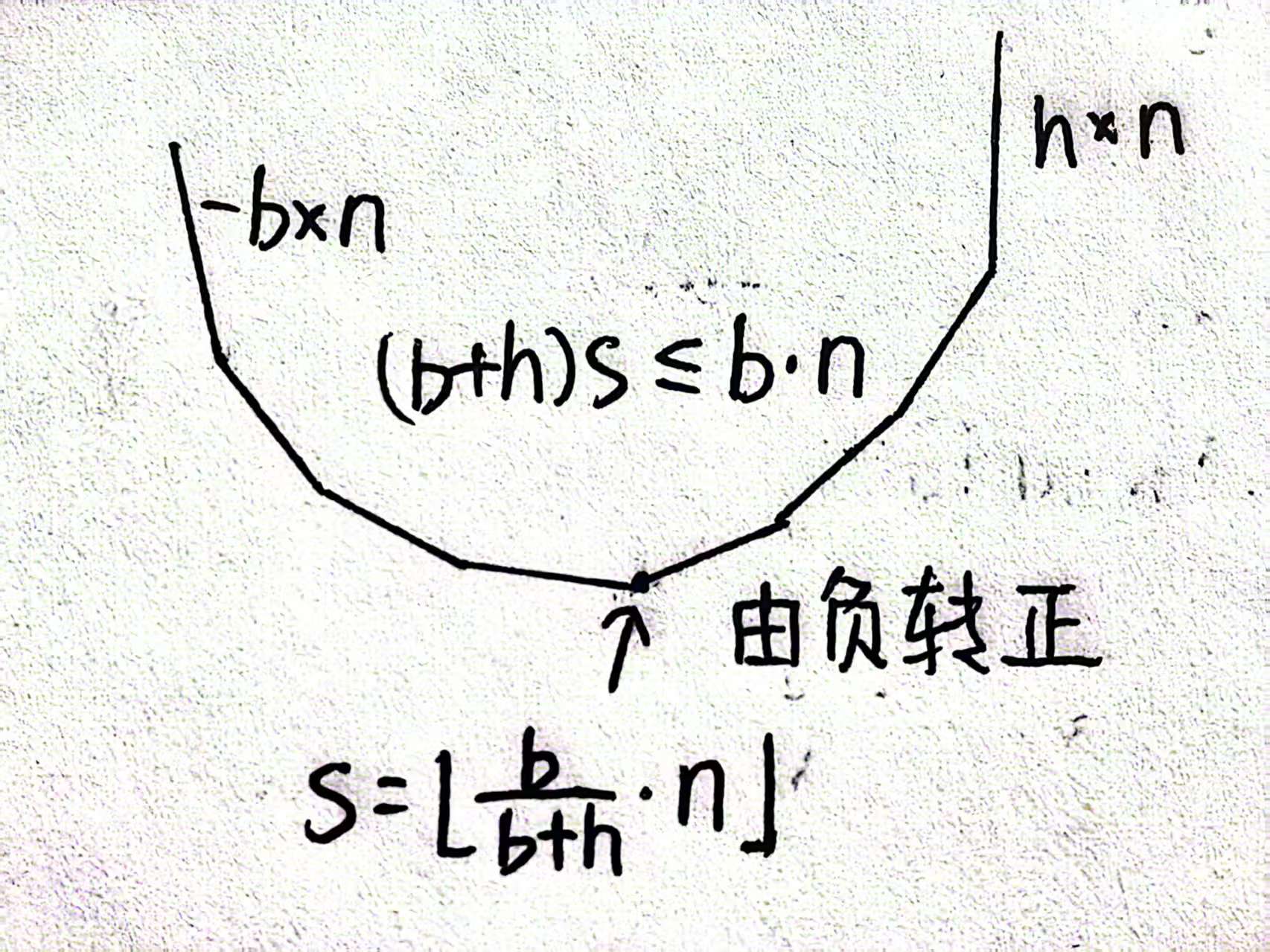
f(a) 是凸且分段线性的 最优解是斜率由负转正。

s* 关键时点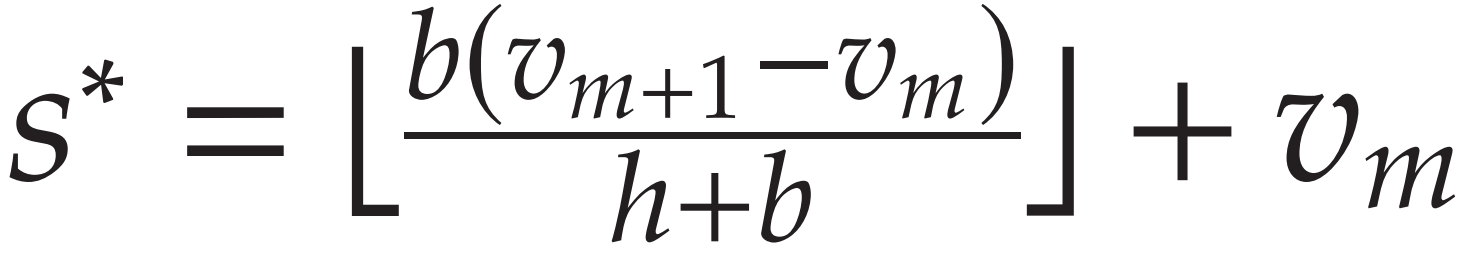

报童模型的关键比率 b/h+b 对 [v_m,v_m+1] 区间进行划分。

Ground Truth a =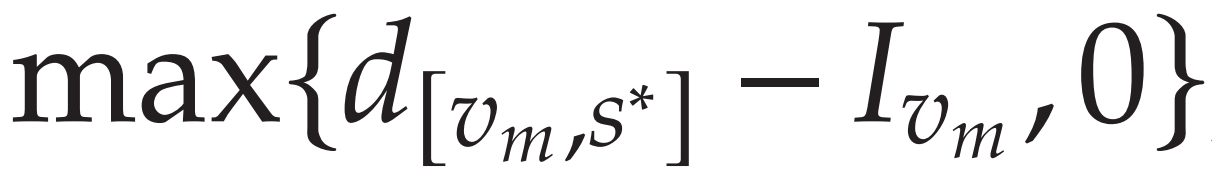 补货量 a = 截止s* 的区间总需求 - 初始存货量 I。

3.2 神经网络结构

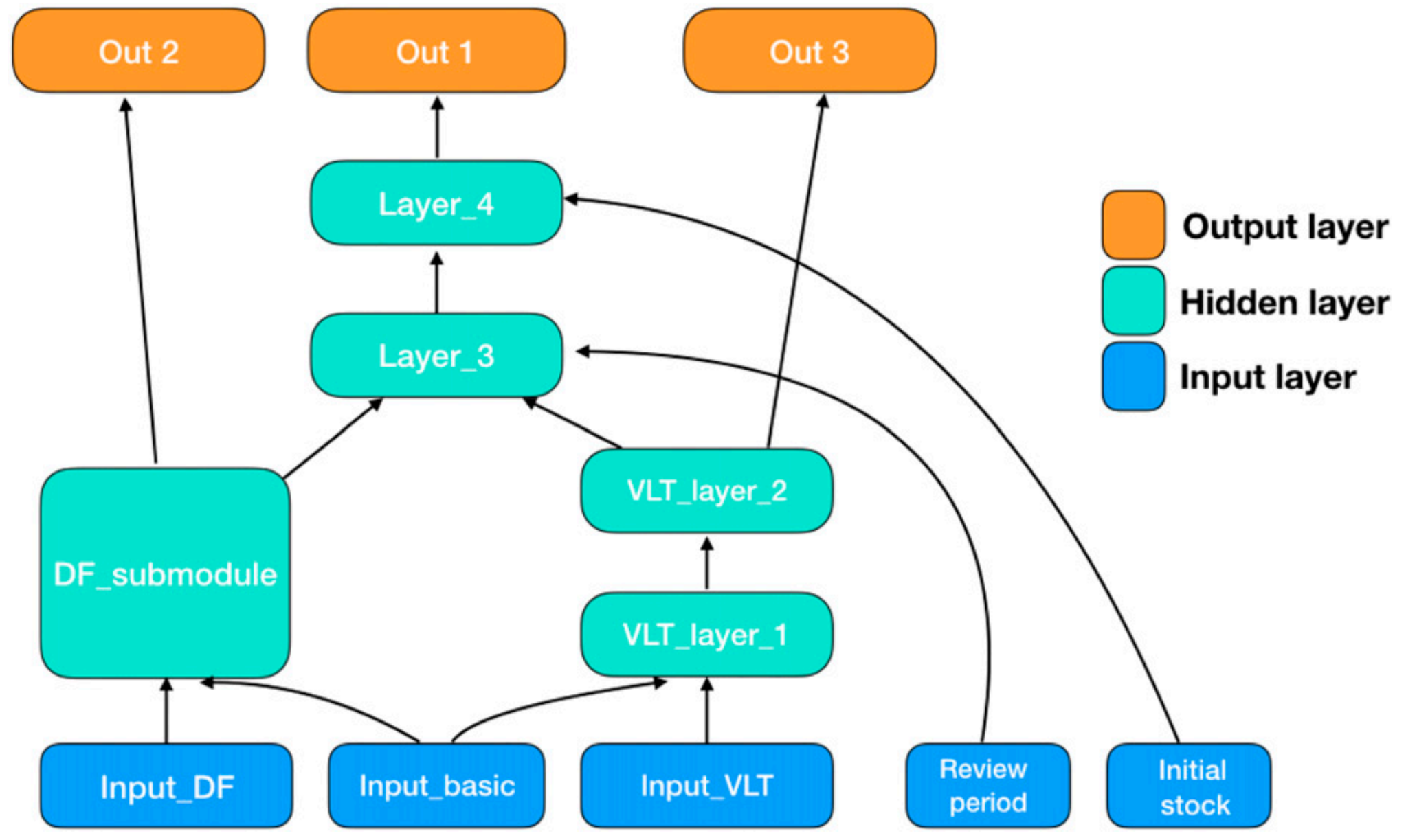
• Input_DF 和 Input_VLT 分别代表与需求和供应商交货期（VLT）相关的特征。

• Input_basic 是一组通用的物品级别特征集合，例如产品类别、仓库位置和品牌名称。

• 剩余的两个特征------盘点周期 和初始库存水平------被直接送入其中一个隐藏层（因为设计上不需要它们与其他特征产生交叉项）。

• 主输出 Out1 ∈ R 代表最终的补货决策。

• 此外，还有两个辅助输出：Out2 作为需求预测，Out3 作为 VLT 预测。

DF_submodule多分位数循环神经网络（MQRNN）。

它接收多个时间序列（例如，需求时间序列、促销时间序列）作为输入，

并生成一组分位数上的每日需求预测作为输出。

其余 layer 为 ReLU 和 dropout 构成的 全连接层。

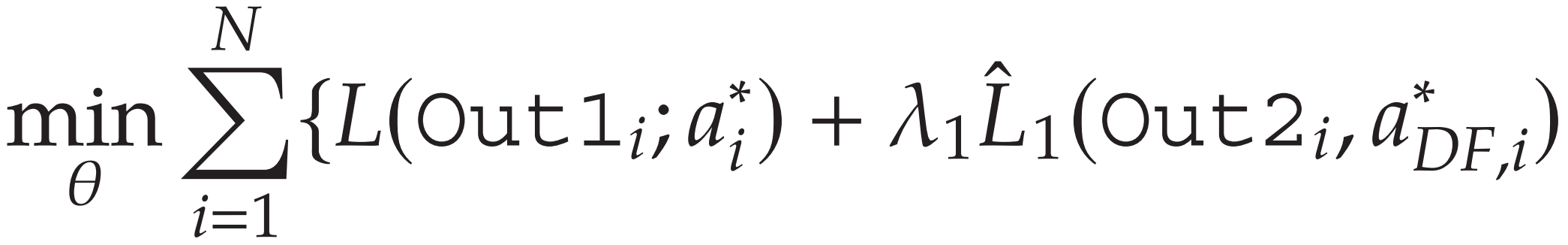
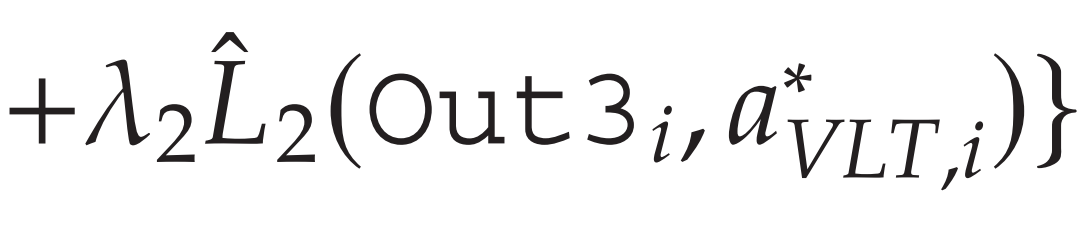
训练目标函数还包含 Out2 和 Out3 目的：

1. 加快参数网络子模块训练收敛

2. 用于监控模型 性能。实际运行 E2E 模型时，观察这两个输出的任何异常有助于决策者发现补货量输出的异常并分析其背后的原因。

结构设计原因：

补货决策是利用需求和 VLT 的信息做出的，而这两者的特征集几乎不重叠且几乎没有关联。

因此，拆成两部分而非一开始就把所有特征完全连接。

这样设计降低了计算复杂度和权重数量的量级，并且强解释性&高性能。

4. 实验结果

4.1 和传统方法、PTO比较（理论基准）Numerical 数值实验

京东（JD.com）的真实运营数据，前三十天 80%训练集，20%验证集，后三十天为测试集。

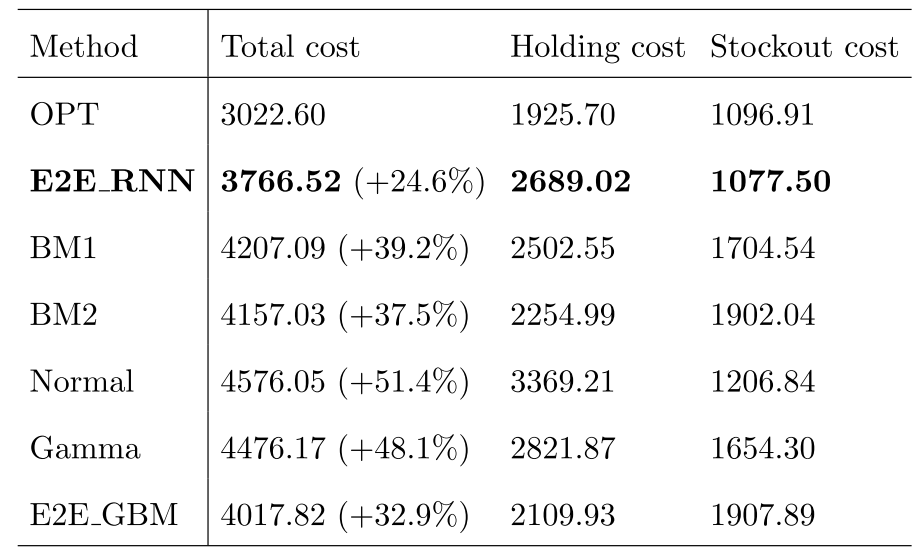
比较：理论最优OPT，两个传统做法，两个PTO，端到端+深度学习/决策树。

第一类：经典库存策略（每天独立同分布）

使用历史数据的统计量（均值、方差）求解参数。

1. BM_normal（正态分布基准）：假设每日需求都服从正态分布。

2. BM_gamma（伽马分布基准） ：假设每日需求都服从伽马分布。伽马分布通常比正态分布更能反映实际需求的正偏态特性（即需求不能为负）。

第二类：两阶段预测-优化（PTO）基准

使用神经网络对 VLT 进行点预测，使用 MQRNN 预测需求。

3. BM1：

* 做法 ：预测两个订单到达点之间的总需求 的分布，然后将其视为单周期的报童问题求解。

4. BM2：

* 做法 ：对未来每一天的需求 进行点预测。

然后在优化阶段，将这些预测值代入一个多期库存成本模型中进行优化。

* 特点 ：对VLT和需求都进行点预测。更贴近真实的多期问题；但丢失不确定性信息。

E2E_GBM 端到端LightGBM一种基于决策树的、在工业界广泛使用的算法。

得到 E2E_RNN 成本远低于其余。

4.2 与京东当前使用的、成熟的两步PTO补货算法比较 -- Field 现场实验

五大性能指标：平均持有成本、平均缺货成本、平均总成本；平均周转率和平均缺货率。

贴近现实，限制更少：

1. 能被已下达但尚未送达的采购订单（即在途补货）所满足时，被视作延迟订单；

无法被在途补货满足，则视为失销。

2. 可能存在订单交叉到达的情况，即订单的到达顺序可能与下单顺序不一致。

数据选取：先选出实验组，再把需求和VLT作为混淆变量，

用"倾向得分匹配法"，得到一个与实验组规模相同的控制组。

1. 根据 t 检验（假设检验比较均值）

原假设：μ_实验组 = μ_对照组 ； t = (X̄_实验组 - X̄_对照组) / SE

2. 线性回归(Is-E2E的权重)

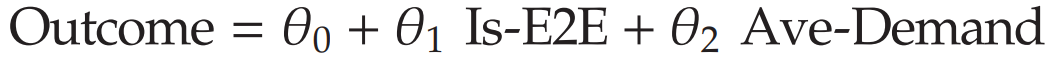
p 值说明这五个变量都显著降低。

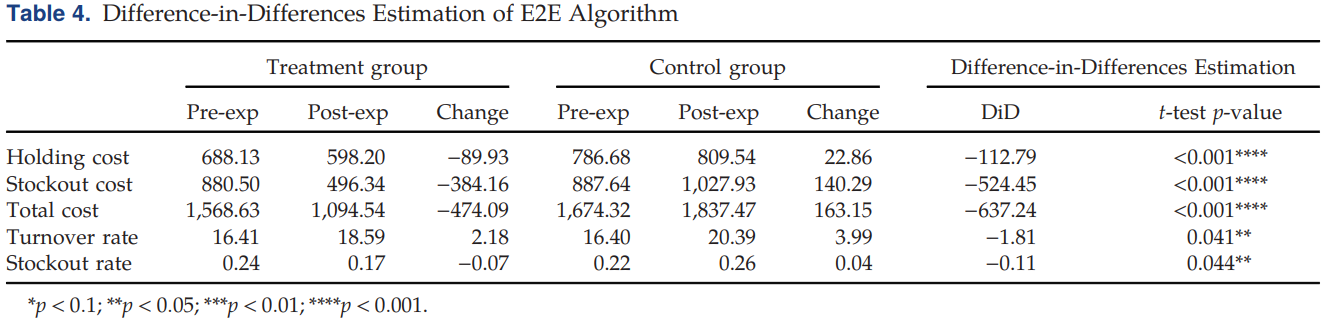
3. Difference-in-Differences （DID模型）

• 方法 ：比较实验组和对照组在实验前 和实验后 的变化差异 。这能有效排除两组之间固有的、不随时间变化的差异对结果的影响，从而更可靠地证明因果关系。

• 将 "实验组的变化" 减去 "对照组的变化" 。这样，共同的外部影响就被抵消了，最终得出纯粹由E2E算法所带来的因果效应。

在2020年3月实验前期，实验组和对照组均采用京东当前的补货算法；

在2020年4月实验后期，实验组采用E2E算法，而对照组仍遵循京东的算法。

5. 总结

• 关键突破 ：摒弃了传统方法对未来需求和在途时间 必须做先验统计分布假设的要求 / PTO 两阶段范式

• 方法论革新 ：提出了一个端到端的深度学习框架来解决库存补货问题。深度学习应用到库存管理。

• 训练理念 ：Ground Truth 是直接学习"全知"最优决策的行为

• 实验证明：数值实验 + 现场实验充分说明优势

• 效果：1.缩短决策流程 2.降低成本和缺货率，提高库存周转率

未来进一步的研究方向：

• 方向一：复杂场景泛化

  • 将E2E模型应用于更复杂的供应链场景，例如多级库存系统 和库存分配问题。

  • 图神经网络 GNN：捕捉不同仓库、零售商之间的空间拓扑关系

  • 多智能体强化学习 ：每个库存点可以被建模为一个智能体，它们通过共享环境状态和奖励信号，学习既利己又协作的策略。

• 方向二：决策范围扩展

  • 构建更强大的E2E模型，使其能联合决策"订购多少"和"何时订购"，这将更贴近实际的库存管理挑战。

  • 将补货决策与供应链的其他环节进行联合优化。