一、使用线性回归进行分类任务
在分类任务中（例如判断肿瘤是良性(0)还是恶性(1) ），如果直接使用线性回归模型：
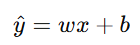
则预测结果可能超出区间 0,1，而概率必须在这个区间内。因此，我们需要一个能够将任意实数映射到 0,1 的函数------这就是Sigmoid函数（逻辑函数）。
二、逻辑回归（Logistic Regression）
1. 肿瘤分类案例
我们的目标是预测"肿瘤为恶性"的概率。
-
设 y=0：肿瘤良性
-
y=1：肿瘤恶性
2. 构建逻辑函数
逻辑回归的核心公式为：
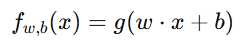
其中：
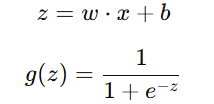
Sigmoid函数 g(z) 的作用是把线性结果 z 转换为一个范围在 (0,1) 之间的概率值。
例如：
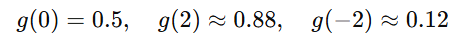
三、边界决策（Decision Boundary）
在逻辑回归中，我们通常选择0.5作为分类边界：
-
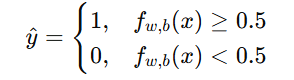
若
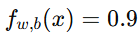，表示恶性概率为 90%，则预测为 1。 -
若
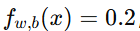，表示恶性概率为 20%，则预测为 0。
线性决策边界对应于一个直线方程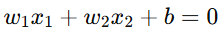 
，
非线性决策边界可以通过加入多项式特征实现（例如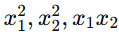 
）。
四、逻辑回归的成本函数（Cost Function）
1. 为什么不能使用平方误差？
若使用平方误差代价函数：
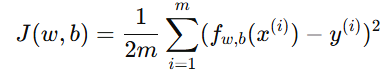
在逻辑回归中会导致非凸函数（Non-convex），训练时可能陷入局部最小值，优化困难。
2. 逻辑回归的损失函数定义
为了让优化问题成为凸函数，我们定义单个样本的损失函数（Loss Function）为：
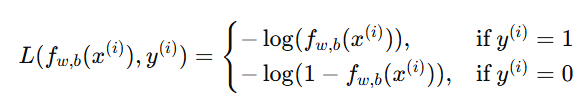
这意味着：
-
若真实标签是 1，模型应尽量让
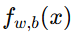靠近 1，否则 
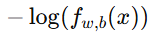会很大； -
若真实标签是 0，模型应让
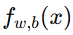靠近 0，否则 
会很大。
五、逻辑回归的简化成本函数
可以把上面的两个情况合并为一个公式：
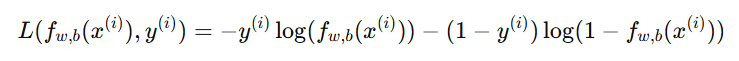
整个训练集的平均成本函数为：
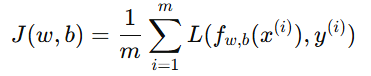
这个函数是凸函数（bowl shape），可以使用梯度下降高效求得最优解。
六、例子：肿瘤预测分类
假设我们有以下肿瘤数据（单特征）：
| 肿瘤大小 x | 是否恶性 y |
|---|---|
| 1.0 | 0 |
| 2.0 | 0 |
| 3.0 | 0 |
| 4.0 | 1 |
| 5.0 | 1 |
我们模型设为：
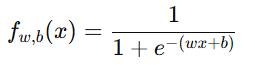
假设训练得到参数 w=1.5,b=−4.0。
当 x=3 时：
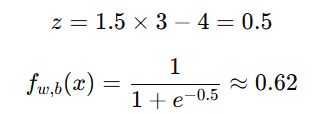
表示"恶性肿瘤"的概率为 62%，因此预测类别为 1（恶性）。
总结：
-
逻辑回归不是"回归"而是"分类"模型；
-
使用 Sigmoid 函数将线性输出转化为概率；
-
损失函数为对数损失（Log Loss），确保优化问题凸；
-
常用梯度下降法最小化 J(w,b)。