机器学习日报02

摘要

本日目标聚焦于两个模块，一个是神经网络如何在TensorFlow中实现，并且探究其训练细节，将整个流程拆解为三个步骤：指定如何根据输入x和参数w、b计算输出；指定损失函数、要求TensorFlow最小化成本函数。第二个模块是寻找sigmoid函数的替代品，ReLu函数、线性激活函数，sigmoid函数，这些函数在各自特定的情况下各司其职，为解决不同的目标而发挥作用

Abstract

Today's focus is on two modules. The first is how neural networks are implemented in TensorFlow, and an exploration of their training details. The entire process is broken down into three steps: specifying how to compute the output based on the input x and parameters w, b; defining the loss function and requiring TensorFlow to minimize the cost function. The second module involves finding alternatives to the sigmoid function, such as the ReLU function, linear activation function, and the sigmoid function itself. These functions each play their respective roles in specific scenarios, serving to address different objectives.

一、TensorFlow实现

我们将继续之前说到过的手动识别数字的例子，识别这些图像是0还是1

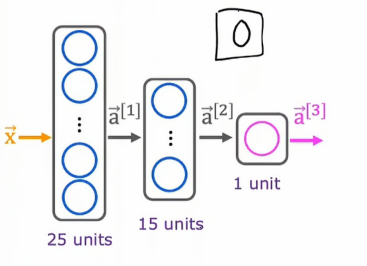
这是我们之前提到的该模型的神经网络架构，下面是实现代码

python 复制代码

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
   model = Sequential([
      Dense(units = 25, activation = 'sigmoid'), /* 第一部分 */
      Dense(units = 15, activation = 'sigmoid'),
      Dense(units = 1, activation = 'sigmoid'),
      ])

from tensorflow.keras.losses import
BinaryCrossentopy 
   model.compile(loss = BinaryCrossentopy()) /* 第二部分*/
   model.fit(X,Y,epoches = 100) /* 第三部分 */

第一部分我们还是比较熟悉的，我们让TensorFlow按顺序连接神经网络的三个层，第一个隐藏层、第二个隐藏层以及输出层。

第二个部分是让TensorFlow编译模型，让TensorFlow编译模型的关键步骤是指定我们要使用的损失函数，在这个例子我们会使用一个名为BinaryCrossentropy的损失函数，称为稀疏分类交叉熵，我们会在下一节详细说明，然后指定好损失函数，它告诉TensorFlow用我们在第一步指定的模型，以及第二部指定的损失函数，来拟合数据集x，y

回到我们之前在学习梯度下降的时候，我们必须决定运行梯度下降多少步或运行多长时间，所以epochs是一个技术术语，用于表示你想运行多少步学习算法如梯度下降。

总而言之，代码第一步是指定模型，告诉TensorFlow如何进行推理计算，第二步是使用特定的损失函数编译模型，第三步是训练模型

1、训练细节

我们来看看训练神经网络的TensorFlow代码实际上在做些什么

在查看训练神经网络的细节之前，让我们来回顾一下我们之前是如何训练逻辑回归模型的

构建逻辑回归模型的第一步是指定如何根据输入x、参数w和b来计算输出，第二步是指定损失函数以及代价函数然后第三步是最小化代价函数，并以此训练逻辑回归函数

这三个步骤同样适用于在TensorFlow中训练神经网络，现在我们来看看这三个步骤如何映射到神经网络训练上

第一步是指定如何根据输入x和参数w和b计算输出，这可以用上面我们说过的dense函数代码来实现，用来指定神经网络，这实际上足以指定前向传播或推理算法中所需的计算

第二步是编译模型，并告知我们想要使用的损失函数，这是用来指定损失函数的代码，这里使用的是二元交叉熵损失函数，对整个训练集取平均值也会给神经网络的成本函数

然后第三步是调用函数尝试将成本函数最小化作为神经网络参数的函数

下面是逻辑回归模型和神经网络模型之间的对比

在训练神经网络的背景下，让我们更加详细地看看这三步

1.1、第一步-----指定如何根据输入x和参数w和b计算输出

这段代码指定了神经网络的整体框架，dense函数告诉我们这一层有几个神经单元，用的激活函数是什么，此外我们还知道每层的w和b的值是多少，所以我们说这段代码指定了神经网络的整体架构，因此告诉TensorFlow一切其需要的用于计算输出x的函数

1.2、第二步----指定损失函数

这将定于我们用来训练神经网络的成本函数，所以对于手写数字分类问题，这是一个二分类问题，我们最常用的损失函数是

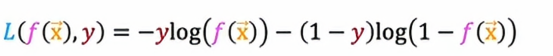
它实际上与我们用于逻辑回归的损失函数相同，其中y是真实标签，有时也被称为目标标签，f(x)现在是神经网络的输出

所以在TensorFlow的术语中，这个函数被称为是二元交叉熵，其语法是让TensorFlow使用这个损失函数来编译神经网络

TensorFlow知道我们想要最小化的成本是平均值，对所有m个训练样本取平均值，所有训练样本的损失平均值，优化这个成本函数使神经网络适应你的二分类数据，如果我们想解决回归而不是分类问题的话，我们可以告诉TensorFlow使用不同的损失函数来编译我们的模型

例如，如果我们有个回归问题，如果我们想最小化平方误差损失，这里是平方误差损失

损失是指如果我们的学习算法是输出f(x)并有目标或真是标签y，那么这是平方误差的一半，然后我们可以在TensorFlow中使用这个损失函数，也就是说使用可能更直观命名的均方误差损失函数，然后TensorFlow将尝试最小化均方误差

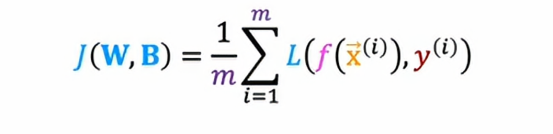
在这个表达式，我们用J(W,B)来表示成本函数，成本函数是神经网络所有参数的函数，我们可以把W看成W1,W2,W3，B包括B1,B2,B3。所以如果我们在优化关于W和B的成本函数，我们会尝试优化神经网络中所有的参数

1.3、第三步----要求TensorFlow最小化成本函数

这让我们想到之前学过的梯度下降算法，如果我们用梯度下降来训练神经网络中的参数，然后我们会在每一层L和每一个单元J上反复地更新

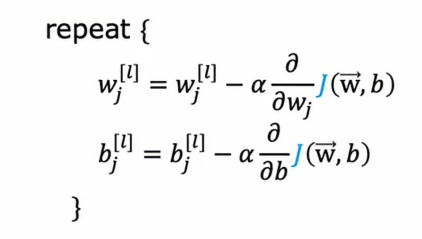
100次梯度下降更新后，我们能够得到一个很好的参数值，所以要使用梯度下降，关键是我们需要计算这些偏导数项，而TensorFlow所做的，事实上，这是神经网络训练中的标准做法，是一种叫做反向传播的算法来计算这些偏导数项，TensorFlow可以为我们完成所有这些事情，它在一个叫fit的函数中实现了所有的反向传播，所以我们需要做的就是调用model.fit.()，并告诉它进行100次迭代或者100个epoch。

事实上，我们之后会学习到TensorFlow可以使用一种比梯度下降更快一点的算法，现在我们知道我们严重依赖这个库来实现神经网络

二、sigmoid函数的替代品

到目前为止，我们所有节点都在使用sigmoid激活函数，应用于隐藏层中以及输出层中，我们以这种方式开始是因为我们正在通过使用逻辑回归并创建大量逻辑回归单元，将它们串联起来以构建神经网络，但如果我们使用其他激活函数，我们的神经网络会变得强大得多，让我们来看看如何做到这一点，回想一下上几节我们学习的需求预测示例，在给定价格，运输成本情况下，营销材料，我们会尝试预测某件商品是否很实惠，如果有很好的认知度和材质，并以此试图预测它是否是畅销商品，但假设了认知度可能是二元的，要么人们知道，要么不知道，但在实际情况下，顾客对于我们的衣服的认知度不是二元的，他们可能有一点了解，稍微了解，非常了解，或者已经是如火如荼的畅销品，所以，与其将认知度建模为二元数字，不如我们将认知度建模为0和1之间的一个数字，认知度应该是一个非负数，从0到非常了解，所以，之前我们曾用这个方程计算第二个隐藏单元的激活值

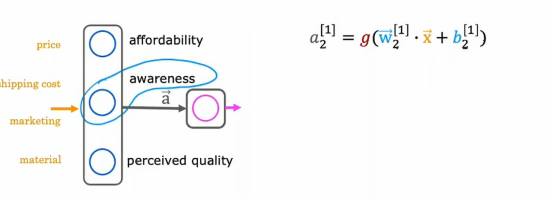
其中，g是sigmoid函数，因此在0~1之间变化

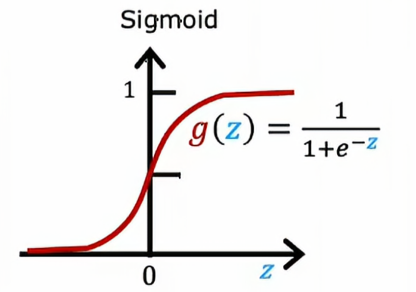
如果我们想让一个激活函数能够取更大的正值，我们可以换用不同的激活函数

1、ReLu函数

事实证明，神经网络中一个非常常见的激活函数就是这个函数，它看起来是这样的

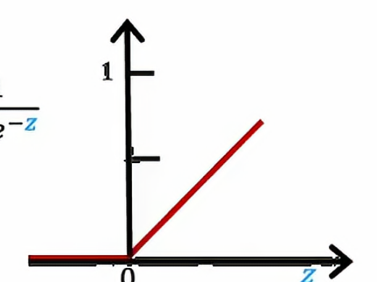
当z在y轴左边时，g(z)就等于0，当z在y轴右边时，g(z)就等于z，这个函数的数学表达式是g(z)等于max(0,z)，这个函数有个名字，叫做ReLu

2、各种激活函数的对比

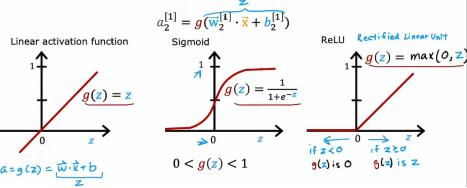
这里需要说明一下，最左边的是线性激活函数，有时我们使用线性激活函数，人们会说我们没有使用任何激活函数，因为，如果a是g(z)，a就等于g(z)=w·x +b/2，所以这个好像根本没有g，所以当我们使用这个线性激活函数时，有些人就会认为我们没有使用任何激活函数

3、如何选择激活函数

3.1、输出层的函数选择

我们来看看如何为神经网络中的不同神经元选择激活函数，我们首先讨论如何为输出层选择激活函数，事实证明取决于目标标签或真实标签Y是什么，对于输出层的激活函数会有一个非常自然的选择

我们可以为神经网络中的不同神经元选择不同的激活函数，具体来说，如果我们正在处理一个分类问题Y是0还是1，这是一个二分类问题，那么sigmoid函数激活函数几乎总是最自然的选择，因为神经网络在这种情况下学习预测Y等于1的概率，就像我们在逻辑回归中一样，所以我的推荐是，如果我们正在处理一个二元分类问题，我们可以考虑在输出层使用sigmoid函数

如果我们在处理一个回归问题，那么我们可能会选择不同的激活函数，例如，如果我们试图预测明天的股票价格将如何相对于今天的股票价格变化，，它可以上涨和下降，所以在这种情况下Y将是一个可正可负的数字，在这种情况下，我更推荐使用线性激活函数

再如果，我想预测房价，房价是一个非负值，这样的话，最值得选择的是ReLu激活函数，因为ReLu函数只能选择非负值

综上所述，我们如何选择激活函数，通常取决于我们试图预测的标签Y是什么，会有一个相当自然的选择

此外，本节我们讨论的方面都是输出层的激活函数的选择，那么隐藏层的函数我们该如何选择呢？

3.2、隐藏层函数的选择

事实证明，ReLu激活函数是训练神经网络时最常见的选择，尽管最初我们用sigmoid激活函数描述了神经网络，因为在神经网络发展的早期，历史中，人们都在许多地方使用sigmoid激活函数，现在这个领域已经发展到更常使用ReLu而几乎不再使用sigmoid函数，唯一的例外是如果输出层的输出是一个二进制，我们会倾向使用sigmoid函数来处理分类问题，这里有几个原因，首先如果我们比较ReLu和sigmoid函数，ReLu的计算会稍微快一点，它只需要零和Z那个值更大一点，而sigmoid的函数则需要取指数运算然后逆运算；第二个原因，更重要的是ReLu函数只要一个方向变平，而sigmoid函数却在两个方向变平，在图像左侧变平，在图像右侧也变平，如果我们用梯度下降算法来训练神经网络，当函数在平坦的时候，梯度下降会变得很慢，虽然我们知道梯度下降算法优化的是成本函数J而不是优化激活函数，，但激活函数是计算的一部分，这样也会影响成本函数J在很多地方变得平坦，并且梯度较小，这回减缓学习速度。在经过研究人员发现，使用ReLu函数可以使神经网络学习地更快，这就是为什么对于大部分从业者，如果想使用什么激活函数用于隐藏层的话，ReLu激活函数已经成为最常用的选择

总的来说，我们在选择神经网络的激活函数时，如果使二进制的分类问题的话，使用sigmoid函数，如果y是一个可以取正值或者负值，则使用线性函数，如果y只能取正值或零，或非负值，则使用ReLu，然后对于隐藏层，我们默认使用ReLu函数，在TensorFlow，我们可以这样实现