Java基础与运算

1.数据存储

关于数据存储与表示
- short 类型与字节 ：图中 "short + short" 的结构，结合 "7 字节" 的标注，可推测是在展示数据类型的字节占用与组合。short类型通常占用 2 字节，两个short共 4 字节，此处可能是在对比不同数据结构的字节消耗，比如下方的 "100 个像素点" 结构（三个 0-255 的区间，每个区间可表示 1 字节，共 3 字节），用于说明不同数据组织方式的存储差异。
- 像素点与颜色："三颜色" 标注与三个 0-255 的区间，对应 RGB 颜色模型，每个颜色通道（红、绿、蓝）用 0-255 的数值表示，组合起来可呈现千万种颜色，这里用于解释像素点的颜色存储原理。
关于存储传输
- "扇区→内存（扇区 4KB）" 以及 "700B、1KB=1024B" 的标注，是在说明存储设备（如硬盘）的扇区与内存之间的数据传输，扇区是硬盘的最小存储单元（通常 4KB），数据以扇区为单位从硬盘传输到内存，同时通过 "700B" 等示例体现存储容量的计量方式（1KB=1024 字节）。

如何存储？--->磁盘储存--->编码表进行存储

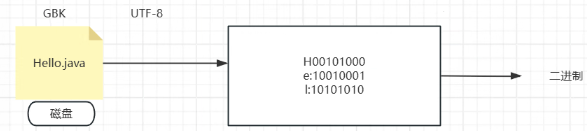
2.变量和常量

变量由三部分组成：数据类型、变量名称和值。这三要素共同决定了变量在内存中的存储方式和可执行的操作。例如，在Java中，int age = 25;表示声明了一个整型变量age，其值为25，在内存中占用4个字节空间。

常量是一种特殊的变量，其值在初始化后不能被修改。在Java中使用final关键字声明常量，其命名通常采用全大写字母和下划线的组合形式，以增强可读性。例如：

java 复制代码

// 声明并初始化常量
final int MAX_RETRY_COUNT = 3;
final double PI = 3.1415926;
final String DEFAULT_USERNAME = "guest";

常量声明后不可修改的特性使其适用于以下场景：

程序中固定不变的配置参数
数学公式中的常数
系统预定义的枚举值

注意：常量一旦初始化后不可修改，因此以下写法是错误的：

java 复制代码

final int A = 10;
A = 11;  // 编译错误：无法修改常量值
// 错误信息：The final local variable A cannot be assigned. It must be blank and not using a compound assignment

在实际开发中，常量的使用可以提高代码的可维护性：

避免魔法数字的出现
便于统一修改
增强代码的可读性

对于类级别的常量，通常使用static final组合声明，例如：

java 复制代码

public class Constants {
    public static final int TIMEOUT = 5000;  // 单位毫秒
    public static final String LOG_PREFIX = "[SYSTEM]";
}

3.数值之间的转换

1.合法转换形式：

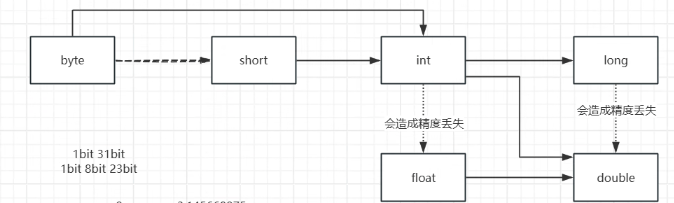
背景与拓展
- 数据类型说明
  - byte：8 位有符号整数，范围 - 128~127。
  - short：16 位有符号整数，范围 - 32768~32767。
  - int：32 位有符号整数，范围 - 2¹⁵~2¹⁵-1。
  - long：64 位有符号整数，范围 - 2³¹~2³¹-1。
  - float：32 位单精度浮点数，用于表示小数，存在精度限制。
  - double：64 位双精度浮点数，精度高于float。
- 转换规则解读
  - 自动转换（隐式转换）：byte可自动转换为short，short可自动转换为int，int可自动转换为long；int可自动转换为float，float可自动转换为double，int也可直接转换为double。这种转换是因为目标类型的表示范围大于或兼容源类型。
  - 精度丢失说明：当int转换为float、int转换为double（实际通常不会丢失，但图中提示需注意）、float转换为double（实际一般不丢失，可能图中强调转换特性）时，会因浮点数的存储机制（如有效位数）造成精度丢失。而byte到short的转换是虚线，可能表示需要注意符号扩展等细节。

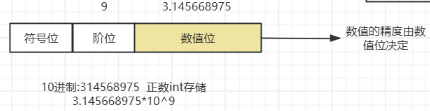
2.非法转换

java 复制代码

package com.qcby.ndspringbootwebsocket.util;

public class AUtil {

    public static void main(String[] args) {
        //byte类型的最大值: 127
        byte a = 127;
        byte b = 1;
        System.out.println(a+b); //128  int类型的数据
        byte c = (byte) (a+b); //强制类型转换: 数值范围由大变小
        System.out.println(c);
    }
}

byte 类型范围 ：byte 是 8 位有符号整数，取值范围为 -128 到 127。代码中 a = 127 表示其最大值。
自动类型提升 ：当 byte 类型变量 a 和 b 参与运算时，会自动提升为 int 类型，因此 a + b 的结果 128 属于 int 类型。
强制类型转换与溢出 ：通过 (byte) 将 int 类型的 128 强制转换为 byte 时，由于超出 byte 的最大值 127，会发生溢出。根据二进制补码规则循环计算，最终结果为 -128。

4.自增操作

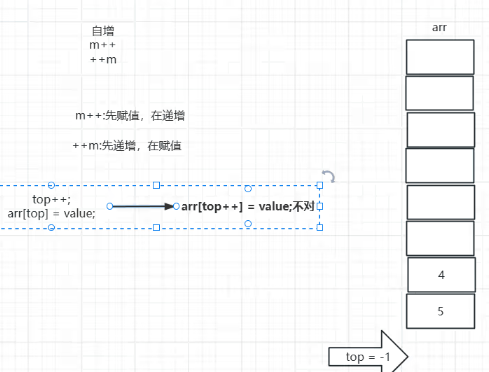
自增操作
- 展示了m++（先赋值再递增）和++m（先递增再赋值）两种自增语法的区别，这是编程中基础的运算符特性，用于控制变量的递增时机。
栈操作示例
- 图中通过top++和数组arr的操作，说明栈结构的元素入栈逻辑。top++是先使用当前top值再递增，而arr[top++] = value的写法是错误的，正确的逻辑应是先确定位置再赋值（arr[++top]=value。右侧的数组arr和top = -1（栈的初始指针位置），进一步辅助理解栈的初始化和元素存储（如数组中已有的 4、5 元素）。

5.位运算

&：按位与操作

规则：两个操作数的对应位全为1时结果为1，否则为0
示例：
- 5 & 3：
  - 5 的二进制：0101
  - 3 的二进制：0011
  - 结果：0001（即1）
应用场景：
- 判断奇偶性：n & 1 结果为1则是奇数，0则是偶数
- 掩码操作：提取特定位的值

|：按位或操作

规则：两个操作数的对应位全为0时结果为0，否则为1
示例：
- 5 | 3：
  - 5 的二进制：0101
  - 3 的二进制：0011
  - 结果：0111（即7）
应用场景：
- 设置特定位为1
- 合并多个标志位

^：按位异或操作

规则：两个操作数的对应位相同时结果为0，不同为1
示例：
- 5 ^ 3：
  - 5 的二进制：0101
  - 3 的二进制：0011
  - 结果：0110（即6）
特性：
- a ^ a = 0
- a ^ 0 = a
- 满足交换律和结合律
应用场景：
- 交换两个变量的值：a ^= b; b ^= a; a ^= b;
- 简单的加密解密

~：按位取反操作

规则：对操作数的每一位（包括符号位）进行取反
示例：
- ~5：
  - 5 的二进制（假设8位）：00000101
  - 取反结果：11111010（即-6的补码表示）
注意事项：
- 结果与使用的数据类型位数有关
- 在Java等语言中，int类型是32位的
应用场景：
- 创建掩码的补集
- 某些位反转操作

6.移位运算

左移运算 (<<)

左移运算符将数值的所有位向左移动指定的位数，右边空出来的位用0填补，左边的高位被舍弃。

运算规则：

数值 << 移动位数
效果相当于原数值乘以2的移动位数次幂（对于正数和负数都适用）

示例： -8 的补码表示：11111000 -8 << 1：11110000（相当于-16） -8 << 2：11100000（相当于-32）

应用场景：

快速计算乘以2的幂次方
在底层编程中用于位操作
某些算法中用于快速计算

右移运算 (>>)

右移运算符将数值的所有位向右移动指定的位数，低位被舍弃，高位的补位取决于原数值的符号。

运算规则：

对于正数：高位补0
对于负数：高位补1（保持符号位不变）
效果相当于原数值除以2的移动位数次幂（向下取整）

示例： -8 的补码表示：11111000 -8 >> 2：

补码：11111000 → 11111110
转换为原码：10000010（即-2）

8 的补码表示：00001000 8 >> 2：

00001000 → 00000010（即2）

注意点：

对于负数，右移运算结果仍为负数
相当于数学上的除法取整操作

无符号右移 (>>>)

无符号右移运算符将数值的所有位向右移动指定的位数，无论原数值是正数还是负数，高位都统一补0。

运算规则：

高位补0
低位舍弃
对于正数，结果与>>相同
对于负数，结果会变成很大的正数

特点：

不考虑符号位
适用于处理无符号数的场景
在Java等语言中可用，但C/C++中没有这个运算符

位运算的好处

java 复制代码

package com.qcby;

import java.util.Arrays;

public class moxie {
    public static void main(String[] args) {
        long start=System.nanoTime();
        System.out.println(2*16);
        long end=System.nanoTime();
        System.out.println(end-start);

        long start1=System.nanoTime();
        System.out.println(2<<4);
        long end1=System.nanoTime();
        System.out.println(end1-start1);
    }
}

位运算可以提高运算速度

Java基础 与运算

1.数据存储

2.变量和常量

3.数值之间的转换

1.合法转换形式：

2.非法转换

4.自增操作

5.位运算

&：按位与操作

|：按位或操作

^：按位异或操作

~：按位取反操作

6.移位运算

左移运算 (<<)

右移运算 (>>)

无符号右移 (>>>)

**位运算的好处**

Java基础与运算

位运算的好处