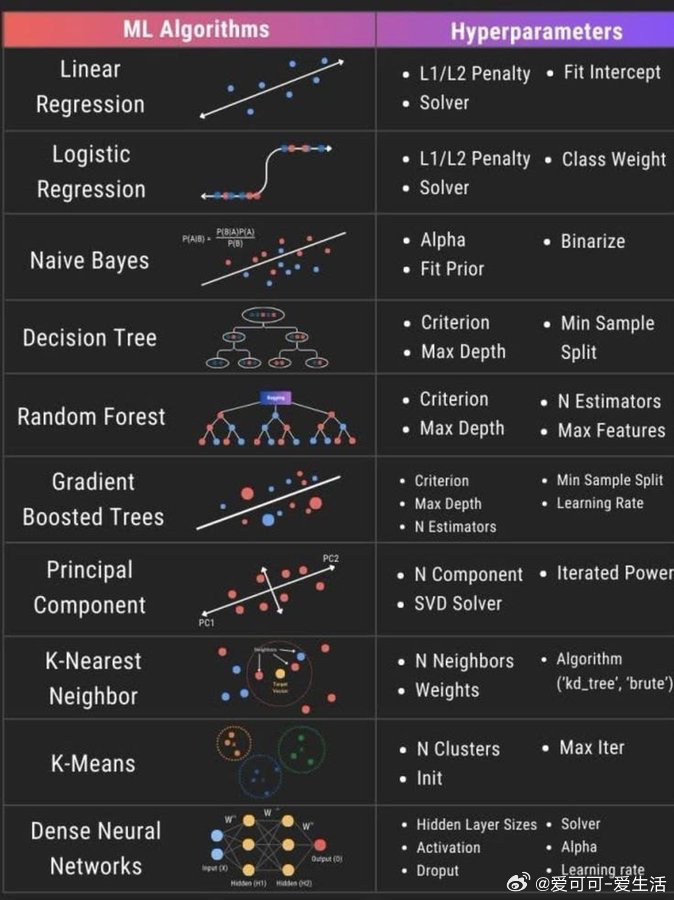
机器学习中,不同算法对应着各自关键的超参数,合理调优这些超参数是提升模型性能的关键。以下是常用算法及其核心超参数概览:
- 线性回归(Linear Regression)
- 关键超参数:L1/L2正则化惩罚项、截距拟合(Fit Intercept)、求解器(Solver)
- 逻辑回归(Logistic Regression)
- 关键超参数:L1/L2正则化、求解器、类别权重(Class Weight)
- 朴素贝叶斯(Naive Bayes)
- 关键超参数:平滑参数Alpha、先验拟合(Fit Prior)、二值化(Binarize)
- 决策树(Decision Tree)
- 关键超参数:分裂准则(Criterion)、最大深度(Max Depth)、最小样本分裂(Min Sample Split)
- 随机森林(Random Forest)
- 关键超参数:分裂准则、最大深度、树的数量(N Estimators)、最大特征数(Max Features)
- 梯度提升树(Gradient Boosted Trees)
- 关键超参数:分裂准则、最大深度、树的数量、最小样本分裂、学习率(Learning Rate)
- 主成分分析(Principal Component)
- 关键超参数:主成分数量(N Component)、迭代幂次法(Iterated Power)、奇异值分解求解器(SVD Solver)
- K近邻(K-Nearest Neighbor)
- 关键超参数:邻居数(N Neighbors)、权重(Weights)、算法选择(如kd-tree、brute)
- K均值聚类(K-Means)
- 关键超参数:簇数(N Clusters)、初始化方式(Init)、最大迭代次数(Max Iter)
- 全连接神经网络(Dense Neural Networks)
- 关键超参数:隐藏层大小、激活函数、Dropout比例、求解器、正则化Alpha、学习率
深度理解并针对具体任务调整这些超参数,不仅能有效提升模型的泛化能力,还能避免过拟合或欠拟合问题。建议结合交叉验证和网格搜索等方法系统调优,助力精准建模。