10 分钟搞定神经网络

本文简单介绍了神经网络的基本原理、组成和基础算法，并通过示例介绍了最简单的神经网络是如何工作的。原文：Learn How Neural Networks Work

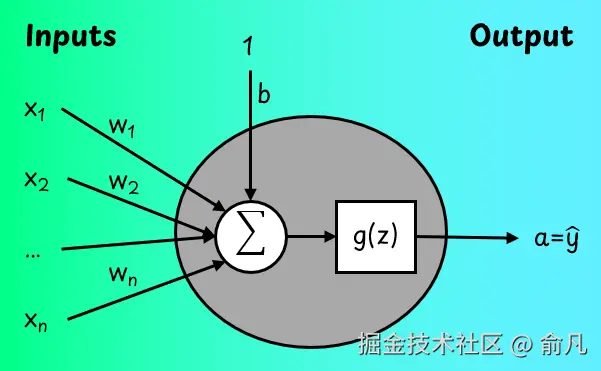
神经网络是人工智能中最重要的组成部分之一，若没有神经网络，像 ChatGPT 这样的大语言模型就不会存在。实际上，几乎所有深度学习模型都在某种程度上使用了神经网络。

这就是为什么了解神经网络的工作原理如此重要。所以，让我们重温一下机器学习的基础知识吧。

神经网络

神经网络是一种受人类大脑工作原理启发而设计的机器学习模型，由许多被称为神经元（neuron）的小单元组成，这些神经元以层的形式相互连接。

我们从最简单的神经网络开始讲起，这种网络只有一个神经元，下图展示了其具体的样子。

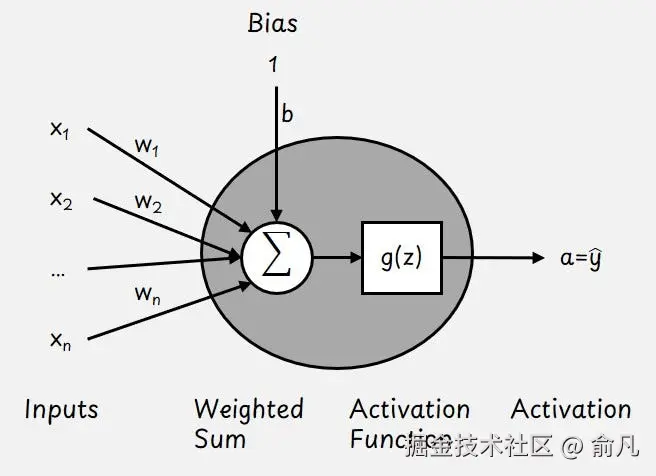
神经元包括输入特征向量x，可学习权重参数向量w和可学习偏置b。

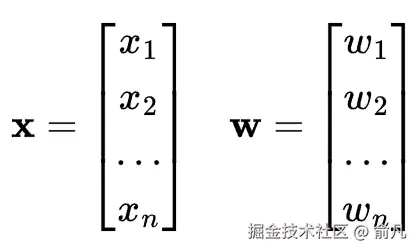
这些参数帮助神经元确定每个输入的重要性。

我们首先计算输入的加权和：

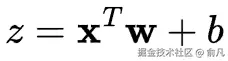
然后通过激活函数g(z)变换输出值z。该函数帮助网络学习非线性模式。神经元的输出称为激活a，在只有一个神经元的情况下，也是模型的输出预测。

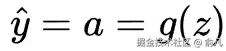
在神经网络中有几种可能的激活函数，每种函数都有不同性质，下图显示了4个示例。

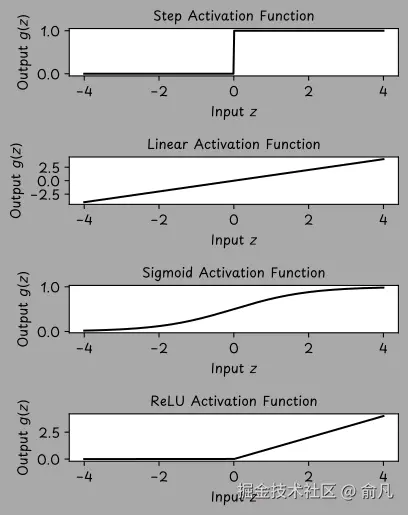
• 在早期的一种被称为"感知机（perceptron）"的神经网络中，使用了阶梯激活函数（step activation function） 。当输入值 z 大于 0 时，神经元会"触发"（输出 1），否则会处于关闭状态（输出 0）。
• 线性激活函数（linear activation function） g(z) = z 与完全不使用激活函数的效果相同。在只有一个神经元的网络中，会产生线性回归模型。
• Sigmoid 激活函数 g(z) = sigma(z) 将任何输入值转换为 0 到 1 之间的范围，这在我们想要建模概率时特别有用。当与单个神经元一起使用时，为我们提供了逻辑回归模型。
• 修正线性单元（ReLU，rectified linear unit） 是一种定义为 g(z) = max(z, 0) 的激活函数。是深度学习中最广泛使用的激活函数。如果输入是正数，ReLU 会让其通过。如果输入是负数，ReLU 输出 0。

根据激活函数的不同，单个神经元可以执行分类或回归任务。例如，它可以表现得像线性或逻辑回归模型。这些都是具有特定激活选择的神经元的特殊情况，从而使得单个神经元成为一种简单但灵活的构建模块。然而，神经网络真正的强大之处在于将众多神经元连接在一起。

现在，我们不再局限于单个神经元，而是来探讨当多个神经元相互连接形成具有若干层的神经网络时情况会如何变化。请看下图示例。这个网络有三层：

• 输入层，即数据进入网络的地方。
• 隐藏层，用于进行中间计算。
• 输出层，用于生成最终结果。

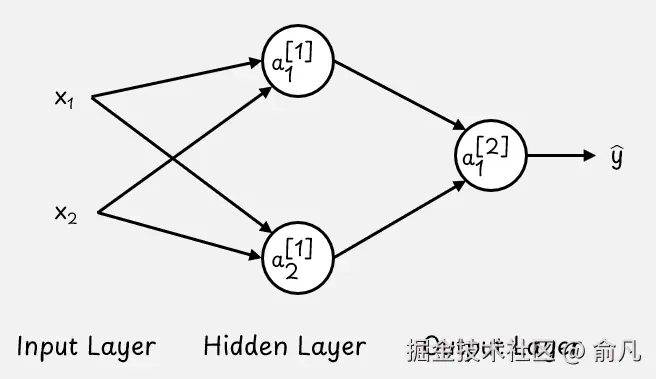
虽然一共有三层，但在描述网络深度时，只计算隐藏层和输出层，因此被称为两层神经网络。这种类型的网络也被称为 前馈神经网络（feedforward neural network） 或 多层感知器（MLP，multi-layer perceptron）。

在这个例子中，隐藏层和输出层都是全连接的。在全连接层（也称为密集层）中，每个神经元都与前一层中的每个神经元相连接。

上述图中的每个圆都代表一个神经元，该神经元具有权重 w、偏差 b 以及激活函数 g(z)。为简便起见，未明确标注偏差和激活函数符号。

现在来看一下如何计算隐藏层中的激活值。

对于隐藏层中的第一个神经元：

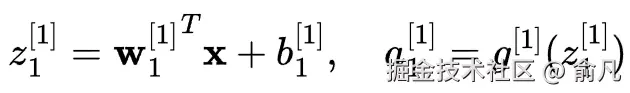
对于隐藏层中的第二个神经元：

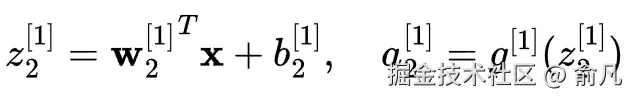
然后用前一层的激活作为输入来计算输出层的激活：

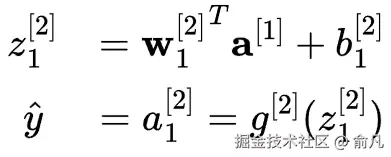
深度神经网络通常具有多种特征、多个隐藏层以及一个或多个输出单元。而"深度"一词仅仅表示该网络具有不止一个隐藏层。

网络的层数和神经元数量越多，就越能学习复杂的模式。然而，更大的网络需要学习的参数也更多。这就增加了对更多训练数据和计算能力的需求，以便有效训练该网络。

设计一个神经网络需要做出一系列重要决策，例如：

• 应包含多少隐藏层（这被称为网络的深度）。
• 每层有多少神经元（即网络的宽度）。
• 应使用何种激活函数。
• 还有许多其他设计细节。

为了说明设计选择对学习的影响，我们通过下图演示一个视觉案例。数据集包含两个类别（标签 y 可以是 1 或 0），这些点以类似月亮的形状排列。

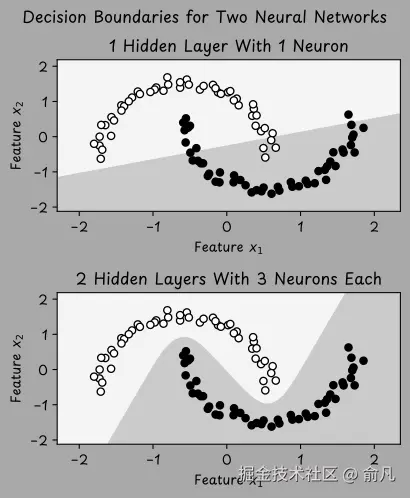
上方的图展示了一个具有一个隐藏层和一个神经元的小型神经网络，它试图对数据进行分类。然而，该网络仅学习到一个简单的直线边界，并不足以区分曲线形状。相比之下，下方的图展示了一个更大的网络，有两层隐藏层，每层有三个神经元。这个网络学习到了一个非线性边界，能够更好的适配数据。

为了减少大型神经网络模型中的过拟合现象，一种常用的正则化策略是"随机失活"。在训练过程中，随机失活会随机"关闭"（通过将激活值乘以零）网络中一定比例的神经元，可以防止模型过度依赖特定神经元，并促使它学习更通用、更稳健的特征。

矩阵表示法

随着神经网络规模的扩大以及数据集容量的增加，单独对每个神经元进行计算变得过于缓慢且效率低下。为了提高效率，我们采用矩阵乘法。

首先将输入特征定义为第 0 个激活值：

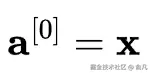
对于神经网络中的每一层，可以使用以下两个方程：

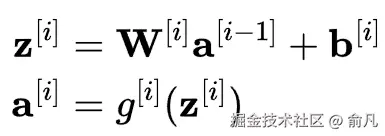
我们来分步骤说明：

• <math xmlns="http://www.w3.org/1998/Math/MathML"> z [ i ] z^{[i]} </math>z[i]：用于计算第 i 层加权总和的向量。
• <math xmlns="http://www.w3.org/1998/Math/MathML"> W [ i ] W^{[i]} </math>W[i]：连接第 [i-1] 层与第 i 层的权重矩阵。此矩阵形状为第 i 层中的神经元数量乘以第 i-1 层的输入数量。
• <math xmlns="http://www.w3.org/1998/Math/MathML"> a [ i − 1 ] a^{[i-1]} </math>a[i−1]：前一层的激活值是当前层的输入。
• <math xmlns="http://www.w3.org/1998/Math/MathML"> b [ i ] b^{[i]} </math>b[i]：第 i 层的偏置项向量。
• <math xmlns="http://www.w3.org/1998/Math/MathML"> g [ i ] g^{[i]} </math>g[i]：第 i 层的激活函数，例如 ReLU 或 Sigmoid。
• <math xmlns="http://www.w3.org/1998/Math/MathML"> a [ i ] a^{[i]} </math>a[i]：第 i 层的输出向量（激活值）。

例如，在我们的神经网络示例中，这里是如何计算第一层（i=1）的 z 的值的：

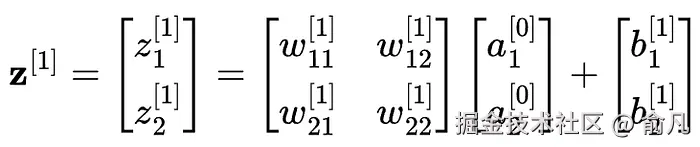
到目前为止，我们只研究了一个数据点。然而在实践中，我们经常希望一次处理一整批数据，这可以通过矩阵乘法完成。

如果将所有输入向量堆叠到一个矩阵 X 中，每一行代表一个输入，那么可以一次计算所有激活：

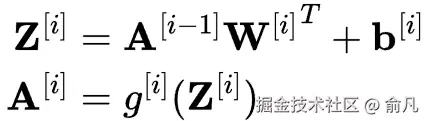
注意：

• Z 和 A 现在是矩阵形式，每一行代表一个样本。
• 通过 <math xmlns="http://www.w3.org/1998/Math/MathML"> W [ i ] T W^{[i]^T} </math>W[i]T（权重矩阵的转置），以使维度匹配。
• 偏置向量会添加到每一行（称为广播操作）。

这种基于矩阵的方法使得深度学习既高效又可扩展，无需逐个遍历神经元，而是可以一次性计算所有输出。这对于 GPU 来说非常理想，因为 GPU 专门设计用于同时处理数千次矩阵运算。

这就是现代人工智能模型能够处理海量数据并拥有数百万（甚至数十亿）参数的原因：因为在其内部运作机制下，不过就是进行大量快速运算的矩阵数学运算而已。

训练神经网络

神经网络通过调整其参数 W 和 b 来学习，以最小化成本（或损失）函数 J(W,b)，该函数会计算训练数据集上的平均预测误差。

具体成本函数取决于任务类型以及在输出层所使用的激活函数。分类任务通常采用交叉熵损失，而回归任务则使用均方误差。

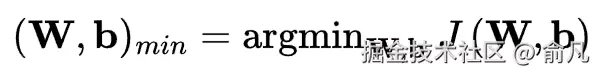
训练始于初始化阶段。通常情况下，偏置项会被设为零，而权重则会以符合均匀分布或正态（高斯）分布的较小随机值进行初始化。这种随机性有助于打破对称性，并使每个神经元能够学习不同内容。

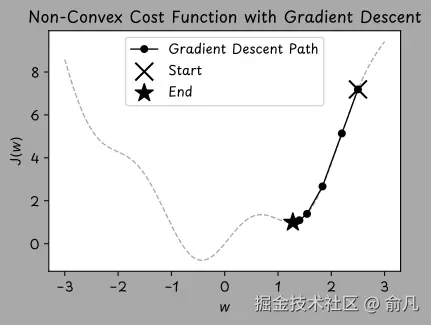
初始化完成后，用一种名为梯度下降的优化算法逐步调整权重和偏置值。梯度下降通过逐步小幅调整模型的权重和偏置值（朝着能减少误差的方向），来最小化成本函数，有点像沿着山谷的坡面向下走，以找到谷底的位置。

Softmax

在许多机器学习任务中，尤其是在分类任务中，神经网络并非仅仅生成单一输出结果。相反，会生成完整的输出向量，针对每个可能类别分别生成一个输出值。例如，ImageNet 数据集曾是深度学习在图像识别领域的早期基准测试，包含的图像可能属于 1000 个类别中的某一个。因此，基于 ImageNet 进行训练的神经网络的输出层必须生成 1000 个分数，每个类别对应一个分数。

我们用 softmax 函数将这些原始分数转换为概率值。softmax 函数将实数向量转换为概率分布，每个输出值都在 0 到 1 之间，且所有输出值总和为 1。因此，softmax 函数通常被用作分类模型输出层的激活函数。

对于输入向量 z ，softmax 函数的计算过程为：

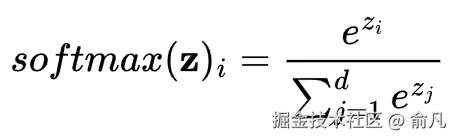
z_i 的值越高，其对应 softmax 输出就越大，但所有输出都是相对于向量中的其他值而言的。

这些值 z_i 通常被称为"对数几率"，是机器学习模型在经过 softmax 函数转换为概率之前所产生的原始分数。

Softmax 示例：

对于 z = [1, 2] 的 softmax 计算结果为：

现在有两个相加起来等于 1 的概率：0.27 + 0.73 = 1 。

神经网络的实际应用

在 Python 中，可以使用 sklearn 中的 MLPClassifier 来训练基本的神经网络。

定义网络并仅基于训练数据对其进行训练，只需要几行代码即可完成。

首先加载示例数据集，将其分为训练集和测试集，并对特征进行标准化处理。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# 创建测试数据集
X, y = make_moons(n_samples=300, noise=0.1, random_state=42)

# 将数据集分为训练集和测试集（70% 训练，30% 测试）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 标准化特征（在机器学习中非常重要）
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

然后构建一个具有一个隐藏层的简单神经网络，该隐藏层包含两个神经元。隐藏层采用 ReLU 激活函数。输出层会自动使用 softmax 激活函数，该函数在进行预测时能给出概率值。

训练过程是通过在训练数据集上调用模型的 fit() 函数来完成，该函数会最小化成本函数。

# 为神经网络设定超参数
hidden_layer_depth = 1  # 隐藏层数量
hidden_layer_width = 2  # 每个隐藏层中的神经元数量

# 创建表示隐藏层大小的元组
hidden_layer_sizes = (hidden_layer_width,) * hidden_layer_depth

# 在训练数据集上训练神经网络
mlp = MLPClassifier(hidden_layer_sizes=hidden_layer_sizes, 
                    activation='relu',  # 隐藏层激活函数
                    solver='sgd',  # 优化算法
                    max_iter=2000)
mlp.fit(X_train, y_train)

神经网络已经完成训练，我们来进行一些预测。

# 进行预测并评估测试集的准确率
y_pred = mlp.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'Test Accuracy: {accuracy * 100:.2f}%')

最后，可以将训练结果可视化。

# Create meshgrid for decision boundary visualization
x_min, x_max = X_test[:, 0].min() - 0.5, X_test[:, 0].max() + 0.5
y_min, y_max = X_test[:, 1].min() - 0.5, X_test[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
                     np.linspace(y_min, y_max, 300))
grid = np.c_[xx.ravel(), yy.ravel()]


# Get probabilities for the grid points to plot decision boundaries
probs = mlp.predict_proba(grid)[:, 1].reshape(xx.shape)


fig, axes = plt.subplots(1, 2, figsize=(12, 6))

# Visualize the decision boundary
ax1 = axes[0]
ax1.contourf(xx, yy, probs, levels=[0, 0.5, 1], alpha=0.3, cmap=plt.cm.Greys)
ax1.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=plt.cm.Greys, edgecolors='k', s=60)
ax1.set_title(f'Decision Boundary\n'
              f'Hidden Layers: {hidden_layer_depth}, Neurons per Layer: {hidden_layer_width}')
ax1.set_xlabel('Feature $x_1$')
ax1.set_ylabel('Feature $x_2$')


# Plot the training loss curve
ax2 = axes[1]
ax2.plot(mlp.loss_curve_)
ax2.set_title('Training Loss Curve')
ax2.set_xlabel('Iteration')
ax2.set_ylabel('Loss')
ax2.grid(True)

# Adjust layout for better visualization
plt.tight_layout()
plt.show()

输出如下结果：

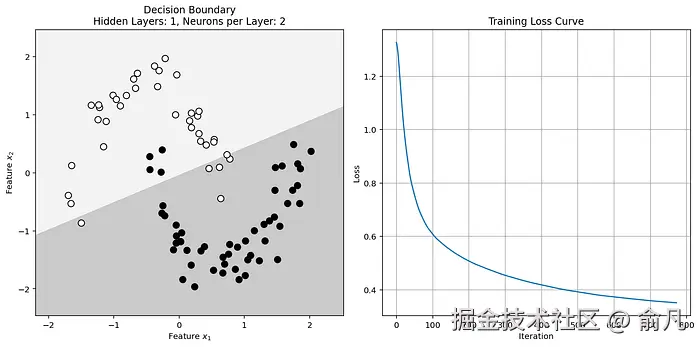
该决策边界不够复杂，无法将数据区分开来。因此，应当通过增加神经网络的深度和/或宽度来提高其复杂度。

---

你好，我是俞凡，在Motorola做过研发，现在在Mavenir做技术工作，对通信、网络、后端架构、云原生、DevOps、CICD、区块链、AI等技术始终保持着浓厚的兴趣，平时喜欢阅读、思考，相信持续学习、终身成长，欢迎一起交流学习。为了方便大家以后能第一时间看到文章，请朋友们关注公众号"DeepNoMind"，并设个星标吧，如果能一键三连(转发、点赞、在看)，则能给我带来更多的支持和动力，激励我持续写下去，和大家共同成长进步！