快速上手大模型：深度学习7（实践：卷积层）

1 全连接层

1.1 基本概念

核心是将输入图像X中所有像素与每个输出像素相连，MLP思想。

式中表示隐藏层中位置(i,j)处的像素，表示输入图像(k,l)处的像素，

，a、b是输入相对输出的偏移，从而将输入与隐藏输出层关联起来

**注意，**此时是多个输入端的像素对应一个隐藏层输出像素。

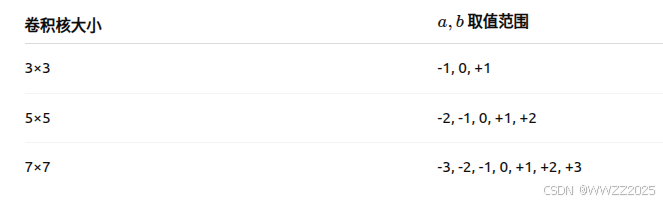
PS.卷积核（kernel）a、b大小的选择规则如下：

1.2 平移不变性

当输入图像的目标在空间上发生小幅移动（平移）时，神经网络的输出结果几乎不变。

意思就是图像上某个东西（如猫）发生平移后还是会被识别出来。

1.3 局部性

在图像中，一个像素点主要受到它周围局部邻域的像素影响，而不是整张图的所有像素。

2 卷积层

（1）卷积层是将输入和核矩阵进行交叉相关，加上偏移后得到输出。卷积层是全连接层的一种变体，它具有局部性 和**平移不变性。**卷积实质上是求的交叉相关。

（2）核矩阵w和偏移b是可学习的参数，核矩阵的大小是超参数（矩阵大小认为决定）。

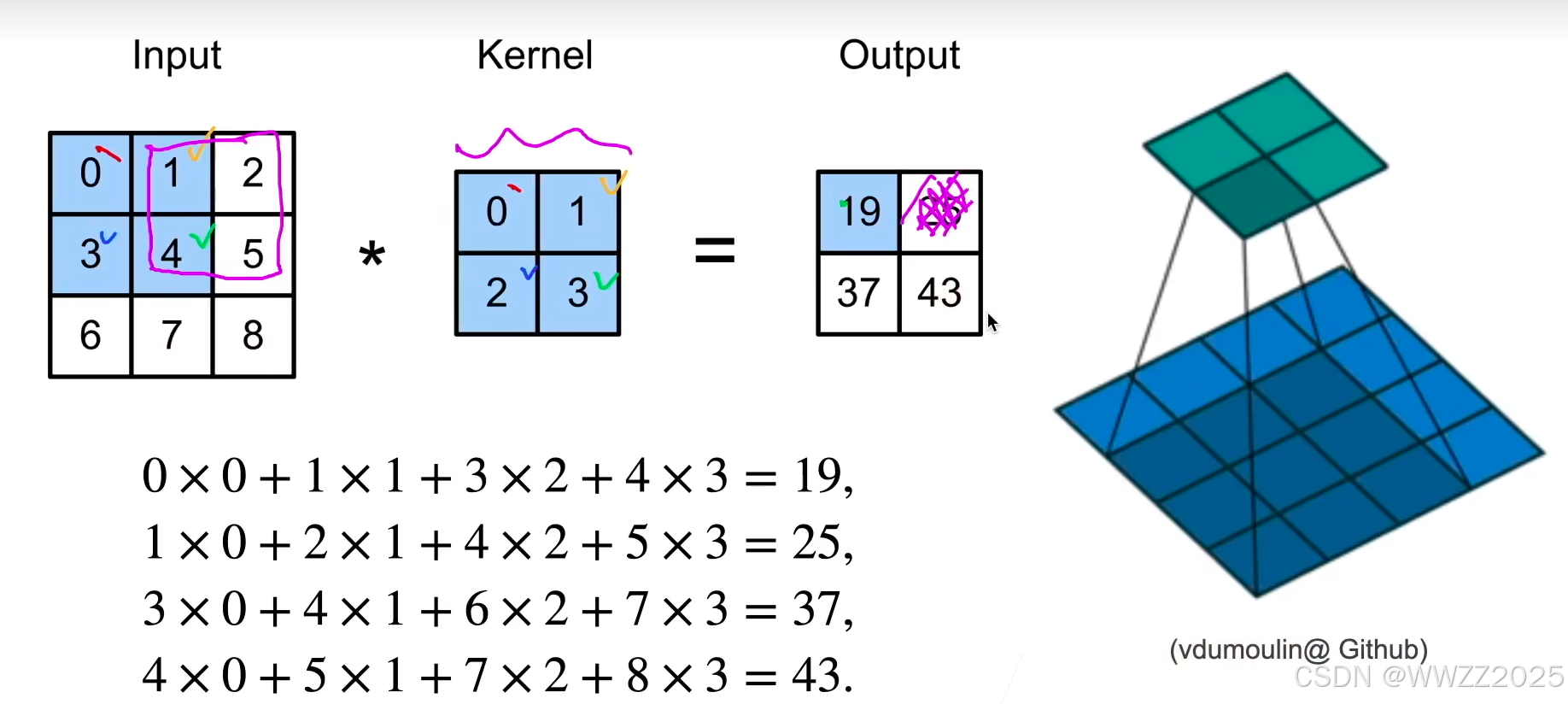
2.1 二维交叉相关

公式：

其中，

：输出特征图在位置(i,j)处的值；

：w为卷积核/滤波器，a、b为卷积核所处的位置，h、w为卷积核的高、宽；

：输入图像中与核当前位置"重叠"的像素。

卷积层使用的运算方法是交叉相关，计算如下。卷积运算是要将卷积核K进行翻转（K矩阵左右对换、上下对换）然后参照交叉相关运算方法运算。交叉相关与卷积运算其实没有关系，但因运算上相差了一个负号，没有实质影响。

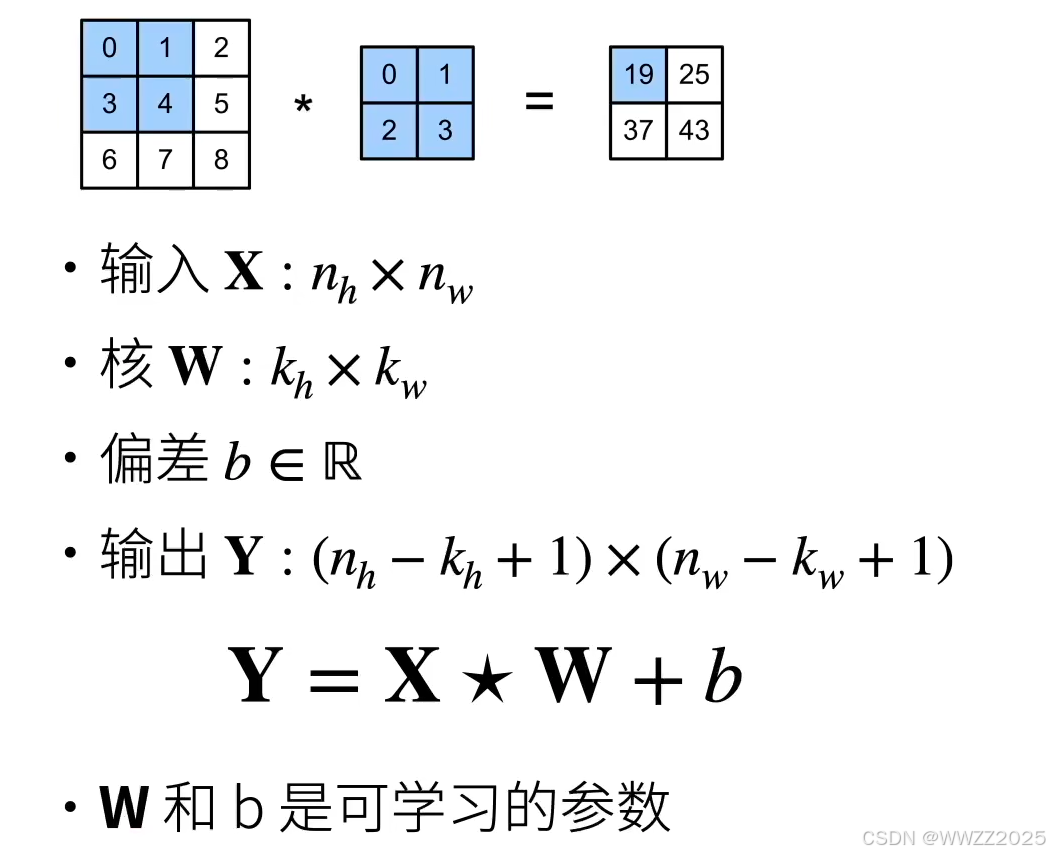
2.2 二维卷积层

公式：

PS.卷积运算实质上是求的交叉相关，两者结果只有负号的影响，大小一致。

2.3 一维交叉相关

公式：

应用：文本、语言、时许序列

2.4 三维交叉相关

公式：

应用：视频、医学图像、气象地图

3 全连接层与卷积层的区别

4 代码

4.1 图像卷积

库：

复制代码

import torch
from torch import nn
from d2l import torch as d2l

定义二维交叉相关运算，代码中K是指核矩阵，即公式里面的w，定义了输出Y的矩阵大小

python 复制代码

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

卷积层：

python 复制代码

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

4.2 应用：边缘检测

（1）随机构建一个6x8的矩阵，X $:, 2:6$ 取0，输出X。1表示白色、0表示黑色。
python 复制代码
X = torch.ones((6, 8))
X[:, 2:6] = 0
X
输出：
python 复制代码
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.],
        [1., 1., 0., 0., 0., 0., 1., 1.]])
（2）定义核函数K
python 复制代码
K = torch.tensor([[1.0, -1.0]])
（3）带入运算，输出Y
python 复制代码
Y = corr2d(X, K)
Y
输出：
python 复制代码
tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])
此时灰度图中黑变白/白变黑的地方就显现出来了，即Y矩阵中列2、列6。注意该方法只可用于检测垂直边缘。

4.3 卷积核生成

由X生成Y的卷积核

python 复制代码

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')