线性代数 | 要义 / 本质（增篇 1）

注：本文为 "线性代数 | 要义 / 本质" 相关重排增版。

如有内容异常，请看原文。

线性代数的本质（篇 1）

一、向量与空间

1. 向量

向量是空间中运动关系的数学表示，正负号用于标识运动方向。例如，二维向量 [ 1 − 2 ] \begin{bmatrix} 1 \\ -2 \end{bmatrix} [1−2] 表示在二维坐标系内，从当前位置沿 x x x 轴正方向移动 1 1 1 个单位，再沿 y y y 轴负方向移动 2 2 2 个单位。该定义可自然推广至 n n n 维空间。

1.1 向量加法：描述两次运动的叠加

向量加法的几何意义是两次运动的叠加，即先按第一个向量完成运动，再按第二个向量完成运动，最终位置为各坐标轴位移的叠加。

示例： [ 1 3 ] + [ 2 4 ] = [ 1 + 2 3 + 4 ] = [ 3 7 ] \begin{bmatrix} 1 \\ 3 \end{bmatrix} + \begin{bmatrix} 2 \\ 4 \end{bmatrix} = \begin{bmatrix} 1+2 \\ 3+4 \end{bmatrix} = \begin{bmatrix} 3 \\ 7 \end{bmatrix} [13]+[24]=[1+23+4]=[37]。

1.2 向量数乘：描述运动幅度的缩放

向量数乘的几何意义是对原向量的运动幅度进行缩放，标量的绝对值表示缩放倍数，符号表示方向是否反转。

示例： 3 × [ 1 2 ] = [ 3 × 1 3 × 2 ] = [ 3 6 ] 3 \times \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} 3 \times 1 \\ 3 \times 2 \end{bmatrix} = \begin{bmatrix} 3 \\ 6 \end{bmatrix} 3×[12]=[3×13×2]=[36]，表示将原向量幅度扩大为原来的 3 3 3 倍。

在数学和物理学中，向量可表示为行向量或列向量，二者几何意义等价，但形式与矩阵运算用途不同：

行向量：用于表示点的坐标或方向，形式为 [ a b ] \begin{bmatrix} a & b \end{bmatrix} [ab]；

列向量：用于矩阵运算，形式为 [ a b ] \begin{bmatrix} a \\ b \end{bmatrix} [ab]。

在二维坐标系中，行向量 [ 1 − 2 ] \begin{bmatrix} 1 & -2 \end{bmatrix} [1−2] 与列向量 [ 1 − 2 ] \begin{bmatrix} 1 \\ -2 \end{bmatrix} [1−2] 均表示从原点 ( 0 , 0 ) (0, 0) (0,0) 出发，先沿 x x x 轴正方向移动 1 1 1 个单位，再沿 y y y 轴负方向移动 2 2 2 个单位，最终位置为 ( 1 , − 2 ) (1, -2) (1,−2)。

2. 线性组合

向量数乘的代数和称为向量的线性组合，任意向量均可表示为一组基向量经数乘后叠加的结果。

示例：

三维空间中任意向量 v \mathbf{v} v，可表示为基向量 i \mathbf{i} i、 j \mathbf{j} j、 k \mathbf{k} k 分别乘以标量 x x x、 y y y、 z z z 后的和，即 v = x i + y j + z k \mathbf{v} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k} v=xi+yj+zk；
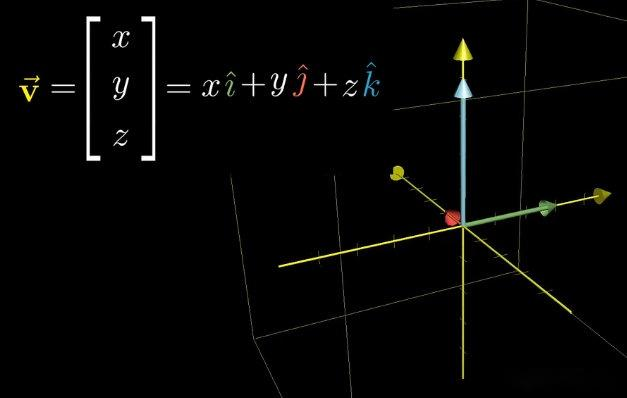
二维向量 [ − 2 1 ] \begin{bmatrix} -2 \\ 1 \end{bmatrix} [−21] 可表示为标准基向量 [ 1 0 ] \begin{bmatrix} 1 \\ 0 \end{bmatrix} [10] 与 [ 0 1 ] \begin{bmatrix} 0 \\ 1 \end{bmatrix} [01] 的线性组合，即 [ − 2 1 ] = − 2 × [ 1 0 ] + 1 × [ 0 1 ] \begin{bmatrix} -2 \\ 1 \end{bmatrix} = -2 \times \begin{bmatrix} 1 \\ 0 \end{bmatrix} + 1 \times \begin{bmatrix} 0 \\ 1 \end{bmatrix} [−21]=−2×[10]+1×[01]。

线性组合可推广为 a v + b w + c u a\mathbf{v} + b\mathbf{w} + c\mathbf{u} av+bw+cu（ a a a、 b b b、 c c c 为标量），计算过程为对向量 v \mathbf{v} v、 w \mathbf{w} w、 u \mathbf{u} u 分别按对应标量缩放，再将结果相加。

u ⃗ \vec{u} u 、 v ⃗ \vec{v} v 、 w ⃗ \vec{w} w 箭头符号在手写中常见；
u \mathbf{u} u、 v \mathbf{v} v、 w \mathbf{w} w粗体符号在印刷品中更常见。

基向量是建立"数组"与"向量"对应关系的关键。当用数组表示向量时，其数值依赖于所选取的基向量。

3. 张成空间

所有可表示为给定向量线性组合的向量集合，称为该组向量张成（span）的空间。

以二维空间为例，设向量 x \mathbf{x} x、 y \mathbf{y} y，若标量 m m m、 n n n 可取任意实数，则线性组合 m x + n y m\mathbf{x} + n\mathbf{y} mx+ny 的张成空间有三种情况：

若 x \mathbf{x} x 与 y \mathbf{y} y 不共线，则张成二维平面空间；
若 x \mathbf{x} x 与 y \mathbf{y} y 共线，则张成一维直线空间；
若 x \mathbf{x} x 与 y \mathbf{y} y 均为零向量，则张成零维点空间。

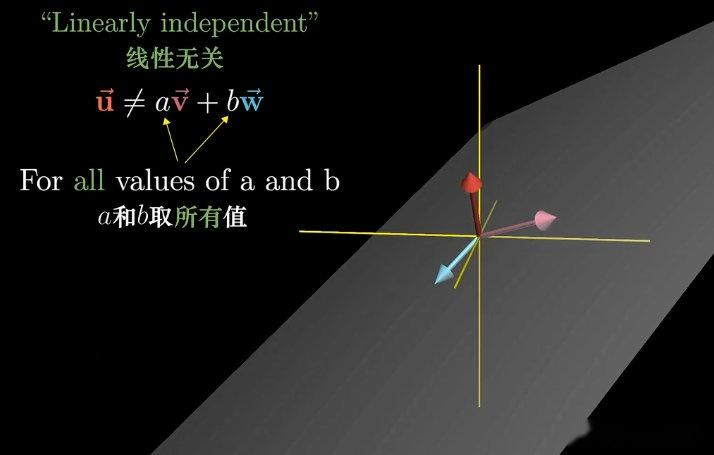
4. 线性相关与线性无关

线性相关 （Linearly Dependent）：存在非全零标量 a a a、 b b b，使得 u = a v + b w \mathbf{u} = a\mathbf{v} + b\mathbf{w} u=av+bw。

设向量组 { α 1 , α 2 , ... , α k } \{\mathbf{\alpha}_1, \mathbf{\alpha}_2, \dots, \mathbf{\alpha}_k\} {α1,α2,...,αk}，若存在至少一个向量可由其余向量线性表示（移除该向量后张成空间维度不变），则称该向量组线性相关。
线性无关 （Linearly Independent）：仅当 a = b = 0 a = b = 0 a=b=0 时， u = a v + b w \mathbf{u} = a\mathbf{v} + b\mathbf{w} u=av+bw 成立。

若向量组中任意向量均不可由其余向量线性表示（每个向量均为张成空间增加新维度），则称该向量组线性无关。

5. 基与维数

在实向量空间 V \mathcal{V} V 中，若集合 B = { v 1 , v 2 , ... , v n } \mathcal{B} = \{ \mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n \} B={v1,v2,...,vn} 同时满足线性无关 与其线性组合能张成整个 V \mathcal{V} V ，则称 B \mathcal{B} B 为 V \mathcal{V} V 的一组基。

5.1 基的充要条件

向量组 B = { v 1 , v 2 , ... , v n } \mathcal{B} = \{ \mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n \} B={v1,v2,...,vn} 成为 V \mathcal{V} V 的基，需同时满足以下两点：

线性无关性 ：对任意标量 c 1 , c 2 , ... , c n ∈ R c_1, c_2, \dots, c_n \in \mathbb{R} c1,c2,...,cn∈R，若 c 1 v 1 + c 2 v 2 + ⋯ + c n v n = 0 c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + \dots + c_n\mathbf{v}_n = \mathbf{0} c1v1+c2v2+⋯+cnvn=0（零向量），则必推出 c 1 = c 2 = ⋯ = c n = 0 c_1 = c_2 = \dots = c_n = 0 c1=c2=⋯=cn=0；
张成性 ：对任意 u ∈ V \mathbf{u} \in \mathcal{V} u∈V，存在唯一一组标量 c 1 , c 2 , ... , c n ∈ R c_1, c_2, \dots, c_n \in \mathbb{R} c1,c2,...,cn∈R，使得 u = c 1 v 1 + c 2 v 2 + ⋯ + c n v n \mathbf{u} = c_1\mathbf{v}_1 + c_2\mathbf{v}_2 + \dots + c_n\mathbf{v}_n u=c1v1+c2v2+⋯+cnvn（即 u \mathbf{u} u 可由 B \mathcal{B} B 线性表示）。

5.2 基的主要性质

不唯一性 ：同一向量空间可存在多组不同基。
例： R 2 \mathbb{R}^2 R2 中， { ( 1 , 0 ) , ( 0 , 1 ) } \{(1,0),(0,1)\} {(1,0),(0,1)}（标准基）与 { ( 1 , 1 ) , ( 1 , − 1 ) } \{(1,1),(1,-1)\} {(1,1),(1,−1)}（非标准基）均为基；
基向量个数的唯一性（维数定义） ：任意基的向量个数固定不变，该个数称为 V \mathcal{V} V 的维数，记为 dim ⁡ ( V ) = n \dim(\mathcal{V}) = n dim(V)=n。
例： R 2 \mathbb{R}^2 R2 维数为 2 2 2，任意基含 2 2 2 个向量； R 3 \mathbb{R}^3 R3 维数为 3 3 3，任意基含 3 3 3 个向量。

5.3 示例（1、2、3 维空间）

（1）1 维空间 R 1 \mathbb{R}^1 R1（数轴）

基的形式：单个非零向量（零向量因线性相关无法作为基）；
示例：取基 { 5 } \{5\} {5}，对任意实数 x ∈ R 1 x \in \mathbb{R}^1 x∈R1，可表示为 x = x 5 × 5 x = \frac{x}{5} \times 5 x=5x×5，满足张成性与线性无关性。

（2）2 维空间 R 2 \mathbb{R}^2 R2（平面）

以两组基为例验证：

基 { ( 1 , 0 ) , ( 0 , 1 ) } \{(1,0),(0,1)\} {(1,0),(0,1)}：
线性无关性： c 1 ( 1 , 0 ) + c 2 ( 0 , 1 ) = ( 0 , 0 ) ⟹ c 1 = c 2 = 0 c_1(1,0) + c_2(0,1) = (0,0) \implies c_1 = c_2 = 0 c1(1,0)+c2(0,1)=(0,0)⟹c1=c2=0；
张成性：任意 ( x , y ) = x ( 1 , 0 ) + y ( 0 , 1 ) (x,y) = x(1,0) + y(0,1) (x,y)=x(1,0)+y(0,1)，可张成 R 2 \mathbb{R}^2 R2。
基 { ( 1 , 1 ) , ( 1 , − 1 ) } \{(1,1),(1,-1)\} {(1,1),(1,−1)}：
线性无关性： c 1 ( 1 , 1 ) + c 2 ( 1 , − 1 ) = ( 0 , 0 ) ⟹ { c 1 + c 2 = 0 c 1 − c 2 = 0 ⟹ c 1 = c 2 = 0 c_1(1,1) + c_2(1,-1) = (0,0) \implies \begin{cases} c_1 + c_2 = 0 \\ c_1 - c_2 = 0 \end{cases} \implies c_1 = c_2 = 0 c1(1,1)+c2(1,−1)=(0,0)⟹{c1+c2=0c1−c2=0⟹c1=c2=0；
张成性：任意 ( x , y ) = x + y 2 ( 1 , 1 ) + x − y 2 ( 1 , − 1 ) (x,y) = \frac{x+y}{2}(1,1) + \frac{x-y}{2}(1,-1) (x,y)=2x+y(1,1)+2x−y(1,−1)，总有解，可张成 R 2 \mathbb{R}^2 R2。

（3）3 维空间 R 3 \mathbb{R}^3 R3（立体空间）

标准基为 B 3 = { [ 1 0 0 ] , [ 0 1 0 ] , [ 0 0 1 ] } \mathcal{B}_3 = \left\{ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \right\} B3=⎩ ⎨ ⎧ 100 , 010 , 001 ⎭ ⎬ ⎫：

线性无关性： c 1 [ 1 0 0 ] + c 2 [ 0 1 0 ] + c 3 [ 0 0 1 ] = [ 0 0 0 ] ⟹ c 1 = c 2 = c 3 = 0 c_1\begin{bmatrix}1\\0\\0\end{bmatrix} + c_2\begin{bmatrix}0\\1\\0\end{bmatrix} + c_3\begin{bmatrix}0\\0\\1\end{bmatrix} = \begin{bmatrix}0\\0\\0\end{bmatrix} \implies c_1 = c_2 = c_3 = 0 c1 100 +c2 010 +c3 001 = 000 ⟹c1=c2=c3=0；
张成性：任意 u = [ x y z ] = x [ 1 0 0 ] + y [ 0 1 0 ] + z [ 0 0 1 ] \mathbf{u} = \begin{bmatrix}x\\y\\z\end{bmatrix} = x\begin{bmatrix}1\\0\\0\end{bmatrix} + y\begin{bmatrix}0\\1\\0\end{bmatrix} + z\begin{bmatrix}0\\0\\1\end{bmatrix} u= xyz =x 100 +y 010 +z 001 ，可张成 R 3 \mathbb{R}^3 R3。

5.4 基的个数与空间维数的对应关系

向量空间维数	基的向量个数	示例（实空间 R n \mathbb{R}^n Rn）
1 维	1 个	R 1 \mathbb{R}^1 R1 的基： { 3 } \{3\} {3}（任意非零实数）
2 维	2 个	R 2 \mathbb{R}^2 R2 的基： { ( 1 , 0 ) , ( 0 , 1 ) } \{(1,0),(0,1)\} {(1,0),(0,1)}
3 维	3 个	R 3 \mathbb{R}^3 R3 的基： { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } \{(1,0,0),(0,1,0),(0,0,1)\} {(1,0,0),(0,1,0),(0,0,1)}

5.5 重要结论

基是"空间的最小生成组"：既无冗余向量（线性无关），又能完整覆盖空间（张成性）；
空间唯一但基不唯一：不同基如同描述同一空间的"不同坐标系"（如 R 2 \mathbb{R}^2 R2 的直角坐标系与斜坐标系）；
维数是空间的固有属性：由基向量个数唯一确定，直接刻画空间的"维度大小"（如 1 维对应直线、2 维对应平面）。

二、矩阵与线性变换

1. 线性变换的定义

变换本质上是函数（function）的一种表述，在线性代数中，研究对象主要是输入与输出均为向量的变换。

从几何视角看，这类变换可理解为：每个输入向量被映射至其对应输出向量的空间位置，且所有向量均遵循同一映射规则。与函数一致，变换满足单值映射性质------任一输入向量仅对应唯一输出向量。

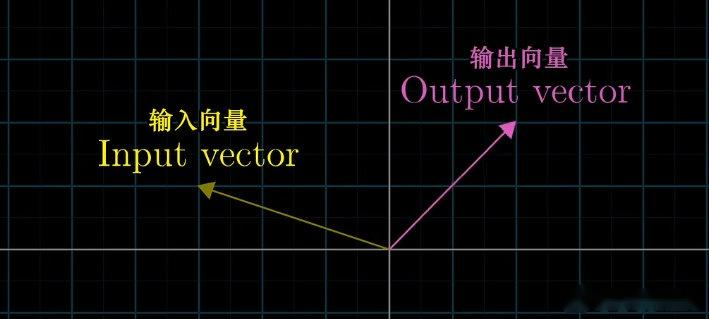
若变换 L : V → W L: V \to W L:V→W 满足以下两条性质，则称为线性变换：

可加性：对任意 u , v ∈ V \mathbf{u}, \mathbf{v} \in V u,v∈V，有 L ( u + v ) = L ( u ) + L ( v ) L(\mathbf{u} + \mathbf{v}) = L(\mathbf{u}) + L(\mathbf{v}) L(u+v)=L(u)+L(v)；
齐次性：对任意 v ∈ V \mathbf{v} \in V v∈V 及标量 k k k，有 L ( k v ) = k L ( v ) L(k\mathbf{v}) = kL(\mathbf{v}) L(kv)=kL(v)。

线性变换的几何特征为：变换后直线仍为直线，且原点位置保持不变。

2. 矩阵向量乘法与线性变换的对应

以二维空间为例，标准基向量 i = [ 1 0 ] \mathbf{i} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} i=[10]、 j = [ 0 1 ] \mathbf{j} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} j=[01]，任意向量 v = [ x y ] \mathbf{v} = \begin{bmatrix} x \\ y \end{bmatrix} v=[xy] 可表示为 v = x i + y j \mathbf{v} = x\mathbf{i} + y\mathbf{j} v=xi+yj。

设线性变换 L L L 将 i \mathbf{i} i 映射为 [ a c ] \begin{bmatrix} a \\ c \end{bmatrix} [ac]，将 j \mathbf{j} j 映射为 [ b d ] \begin{bmatrix} b \\ d \end{bmatrix} [bd]，根据线性变换的性质：
L ( v ) = L ( x i + y j ) = x L ( i ) + y L ( j ) = x [ a c ] + y [ b d ] = [ a x + b y c x + d y ] L(\mathbf{v}) = L(x\mathbf{i} + y\mathbf{j}) = xL(\mathbf{i}) + yL(\mathbf{j}) = x\begin{bmatrix} a \\ c \end{bmatrix} + y\begin{bmatrix} b \\ d \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix} L(v)=L(xi+yj)=xL(i)+yL(j)=x[ac]+y[bd]=[ax+bycx+dy]

将变换后的基向量作为列向量构成矩阵 [ a b c d ] \begin{bmatrix} a & b \\ c & d \end{bmatrix} [acbd]，则上述运算可表示为矩阵向量乘法：

a b c d \] \[ x y \] = \[ a x + b y c x + d y \] \\begin{bmatrix} a \& b \\\\ c \& d \\end{bmatrix} \\begin{bmatrix} x \\\\ y \\end{bmatrix} = \\begin{bmatrix} ax + by \\\\ cx + dy \\end{bmatrix} \[acbd\]\[xy\]=\[ax+bycx+dy

由此可知：

一个 2 × 2 2 \times 2 2×2 矩阵唯一确定一个二维线性变换，矩阵的列向量为变换后的标准基向量；
矩阵向量乘法本质是"基向量缩放后叠加"，即计算线性变换作用于向量的结果。

以二维向量 v = [ − 1 2 ] \mathbf{v} = \begin{bmatrix} -1 \\ 2 \end{bmatrix} v=[−12] 为例，其本质是 − 1 × i + 2 × j -1 \times \mathbf{i} + 2 \times \mathbf{j} −1×i+2×j（ i \mathbf{i} i、 j \mathbf{j} j 为二维标准基）。线性变换满足"网格平行且等距"的性质，因此变换后向量仍保持原线性组合关系，即变换后的向量为 − 1 × L ( i ) + 2 × L ( j ) -1 \times L(\mathbf{i}) + 2 \times L(\mathbf{j}) −1×L(i)+2×L(j)。

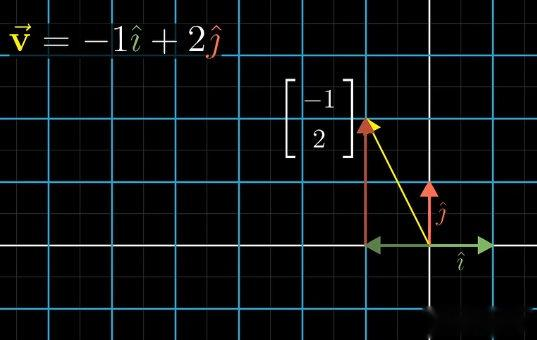
若变换后基向量 i \mathbf{i} i 为 [ 1 − 2 ] \begin{bmatrix} 1 \\ -2 \end{bmatrix} [1−2]、 j \mathbf{j} j 为 [ 3 0 ] \begin{bmatrix} 3 \\ 0 \end{bmatrix} [30]，则变换后的向量 v \mathbf{v} v 为：
− 1 ⋅ [ 1 − 2 ] + 2 ⋅ [ 3 0 ] = [ − 1 + 6 2 + 0 ] = [ 5 2 ] -1 \cdot \begin{bmatrix} 1 \\ -2 \end{bmatrix} + 2 \cdot \begin{bmatrix} 3 \\ 0 \end{bmatrix} = \begin{bmatrix} -1 + 6 \\ 2 + 0 \end{bmatrix} = \begin{bmatrix} 5 \\ 2 \end{bmatrix} −1⋅[1−2]+2⋅[30]=[−1+62+0]=[52]

由此可知，只要确定变换后基向量 i \mathbf{i} i 与 j \mathbf{j} j 的形式，即可推导任意二维向量经过该变换后的结果。对于任意二维向量 [ x y ] \begin{bmatrix} x \\ y \end{bmatrix} [xy]，其变换过程为：

x y \] → x L ( i ) + y L ( j ) = x \[ 1 − 2 \] + y \[ 3 0 \] = \[ x + 3 y − 2 x \] \\begin{bmatrix} x \\\\ y \\end{bmatrix} \\to xL(\\mathbf{i}) + yL(\\mathbf{j}) = x\\begin{bmatrix} 1 \\\\ -2 \\end{bmatrix} + y\\begin{bmatrix} 3 \\\\ 0 \\end{bmatrix} = \\begin{bmatrix} x + 3y \\\\ -2x \\end{bmatrix} \[xy\]→xL(i)+yL(j)=x\[1−2\]+y\[30\]=\[x+3y−2x

2.1 常见线性变换示例

旋转变换 ：

将空间逆时针旋转 9 0 ∘ 90^\circ 90∘，标准基向量 i \mathbf{i} i 映射为 [ 0 1 ] \begin{bmatrix} 0 \\ 1 \end{bmatrix} [01]， j \mathbf{j} j 映射为 [ − 1 0 ] \begin{bmatrix} -1 \\ 0 \end{bmatrix} [−10]，对应的变换矩阵为 [ 0 − 1 1 0 ] \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} [01−10]；

任意向量经过逆时针 9 0 ∘ 90^\circ 90∘ 旋转后的结果，可通过该向量与旋转矩阵相乘得到。
剪切变换 ：

保持 i \mathbf{i} i 不变（映射为 [ 1 0 ] \begin{bmatrix} 1 \\ 0 \end{bmatrix} [10]），将 j \mathbf{j} j 映射为 [ 1 1 ] \begin{bmatrix} 1 \\ 1 \end{bmatrix} [11]，对应的变换矩阵为 [ 1 1 0 1 ] \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} [1011]；

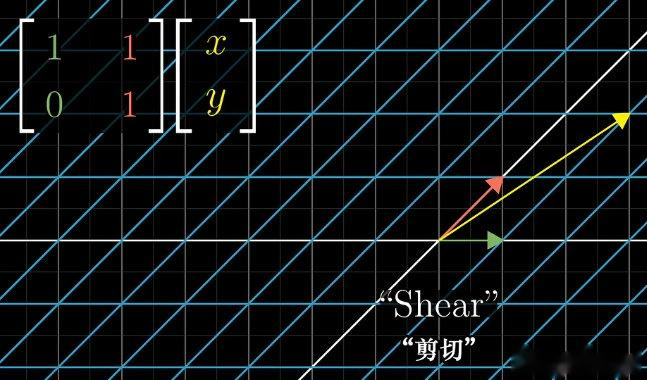
任意向量经过该剪切变换后的结果，可通过该向量与剪切矩阵相乘得到。

3. 矩阵乘法与线性变换的复合

矩阵乘法关联的是线性变换的复合，即两个线性变换相继作用的结果，这种复合可通过矩阵乘积表示，并需遵循特定规则与性质。

3.1 复合变换的基本概念

设线性变换 L 1 L_1 L1 对应矩阵 A A A，线性变换 L 2 L_2 L2 对应矩阵 B B B。如果先执行 L 1 L_1 L1、再执行 L 2 L_2 L2，则该复合变换记为 L = L 2 ∘ L 1 L = L_2 \circ L_1 L=L2∘L1。

复合变换的矩阵表示：该复合变换对应的矩阵为 B × A B \times A B×A，矩阵乘法的顺序与线性变换的执行顺序反向（即"从右向左"）；
几何意义：矩阵乘法本质是"线性变换的相继作用"。例如"先旋转变换、后剪切变换"：旋转变换（对应 L 1 L_1 L1）的矩阵 A = [ 0 − 1 1 0 ] A = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} A=[01−10]（向量逆时针旋转 9 0 ∘ 90^\circ 90∘），剪切变换（对应 L 2 L_2 L2）的矩阵 B = [ 1 1 0 1 ] B = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} B=[1011]，则复合变换的矩阵为 B × A = [ 1 − 1 1 0 ] B \times A = \begin{bmatrix} 1 & -1 \\ 1 & 0 \end{bmatrix} B×A=[11−10]。

3.2 复合变换的关键性质

3.2.1 复合变换的矩阵计算推导

对任意向量 v \mathbf{v} v，复合变换的作用过程可通过矩阵运算推导： L ( v ) = L 2 ( L 1 ( v ) ) = B ( A v ) = ( B A ) v L(\mathbf{v}) = L_2(L_1(\mathbf{v})) = B(A\mathbf{v}) = (BA)\mathbf{v} L(v)=L2(L1(v))=B(Av)=(BA)v，直接印证"复合变换矩阵为对应线性变换矩阵乘积"的规则。

3.2.2 矩阵乘法的交换律

矩阵乘法不满足普遍交换律（通常 A B ≠ B A AB \neq BA AB=BA），需从以下两方面理解：

"通常 A B ≠ B A AB \neq BA AB=BA"的原因：
- 线性变换的顺序依赖性：变换效果与执行顺序强相关（如先剪切再旋转，与先旋转再剪切，结果不同）；
- 代数计算规则限制：矩阵乘法遵循"前矩阵行 × 后矩阵列"，交换顺序后参与运算的行和列对应关系改变。例如 A = [ 1 2 3 4 ] A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} A=[1324]， B = [ 5 6 7 8 ] B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} B=[5768]，计算得 A B = [ 19 22 43 50 ] AB = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix} AB=[19432250]， B A = [ 23 34 31 46 ] BA = \begin{bmatrix} 23 & 34 \\ 31 & 46 \end{bmatrix} BA=[23313446]，二者元素不同。
满足 A B = B A AB = BA AB=BA 的特殊场景：
- 场景 1：其中一个矩阵为单位矩阵 I \mathbf{I} I（如 I = [ 1 0 0 1 ] \mathbf{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} I=[1001]），对任意矩阵 A A A 有 A I = I A = A AI = IA = A AI=IA=A；
- 场景 2：其中一个矩阵为零矩阵 O \mathbf{O} O，对任意矩阵 A A A 有 A O = O A = O AO = OA = O AO=OA=O；
- 场景 3：两个矩阵均为对角矩阵（如 A = [ a 0 0 b ] A = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} A=[a00b]， B = [ c 0 0 d ] B = \begin{bmatrix} c & 0 \\ 0 & d \end{bmatrix} B=[c00d]），则 A B = B A = [ a c 0 0 b d ] AB = BA = \begin{bmatrix} ac & 0 \\ 0 & bd \end{bmatrix} AB=BA=[ac00bd]；
- 场景 4：矩阵与自身的幂次相乘（如 A 2 × A 3 = A 3 × A 2 = A 5 A^2 \times A^3 = A^3 \times A^2 = A^5 A2×A3=A3×A2=A5）。

3.3 矩阵乘法的计算逻辑

设矩阵 A = [ a b c d ] A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} A=[acbd]，矩阵 B = [ e f g h ] B = \begin{bmatrix} e & f \\ g & h \end{bmatrix} B=[egfh]，则 B A BA BA 的列向量为" A A A 的列向量经 B B B 变换后的结果"：

B A BA BA 的第一列： B × [ a c ] = [ a e + c g a f + c h ] B \times \begin{bmatrix} a \\ c \end{bmatrix} = \begin{bmatrix} ae + cg \\ af + ch \end{bmatrix} B×[ac]=[ae+cgaf+ch]；
B A BA BA 的第二列： B × [ b d ] = [ b e + d g b f + d h ] B \times \begin{bmatrix} b \\ d \end{bmatrix} = \begin{bmatrix} be + dg \\ bf + dh \end{bmatrix} B×[bd]=[be+dgbf+dh]；
最终 B A = [ a e + c g b e + d g a f + c h b f + d h ] BA = \begin{bmatrix} ae + cg & be + dg \\ af + ch & bf + dh \end{bmatrix} BA=[ae+cgaf+chbe+dgbf+dh]。

4. 三维空间的线性变换

三维线性变换的逻辑与二维一致，关键性质包括：

一个 3 × 3 3 \times 3 3×3 矩阵唯一确定一个三维线性变换，矩阵的列向量为变换后的标准基向量（ i = [ 1 0 0 ] \mathbf{i} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} i= 100 、 j = [ 0 1 0 ] \mathbf{j} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} j= 010 、 k = [ 0 0 1 ] \mathbf{k} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} k= 001 ）；
矩阵向量乘法：对 3 × 3 3 \times 3 3×3 矩阵 A A A 与三维向量 v = [ x y z ] \mathbf{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} v= xyz ， A v A\mathbf{v} Av 为 A A A 的列向量分别乘以 x x x、 y y y、 z z z 后的和；
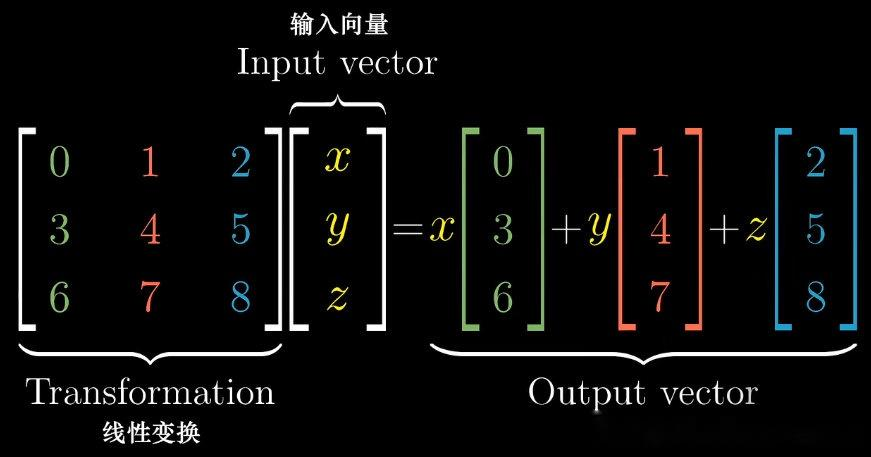
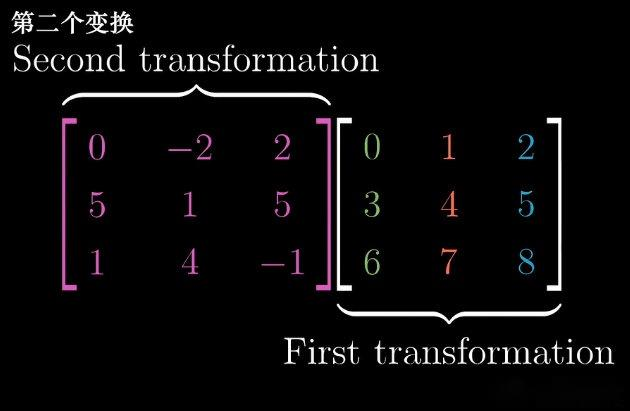
矩阵乘法：两个 3 × 3 3 \times 3 3×3 矩阵 A A A、 B B B 的乘积 B A BA BA，其列向量为" A A A 的列向量经 B B B 变换后的结果"；

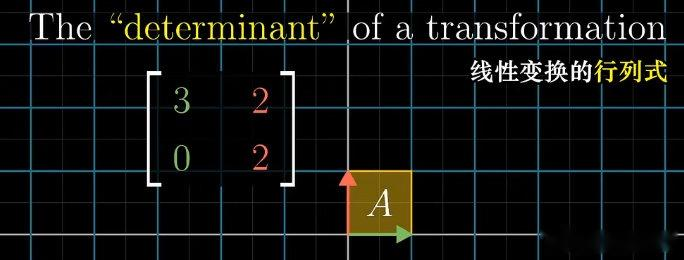
5. 行列式的定义与几何意义

设线性变换对应的矩阵为 A A A，将空间中任意区域（如二维平面的平行四边形、三维空间的平行六面体）变换后，"变换后区域的面积（或体积）"与"原区域的面积（或体积）"的比值，称为矩阵 A A A 的行列式，记作 det ⁡ ( A ) \det(A) det(A)。

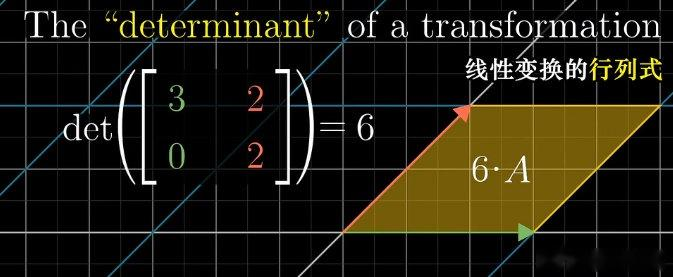
5.1 行列式的符号与数值意义

行列式的意义是描述线性变换的"有向缩放因子 "或"有向体积变化率"，具体分三种情况：

（1）当 det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0 时

几何意义：线性变换为降维变换（不可逆变换、奇异变换）。二维空间中变换后图形压缩为直线或点，三维空间中压缩为平面、直线或点（变换后像空间维度小于原空间）；
代数意义：矩阵 A A A 的列（或行）向量组线性相关，秩小于其维数，不可逆，齐次线性方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 有非零解。

（2）当 det ⁡ ( A ) > 0 \det(A) > 0 det(A)>0 时

几何意义：线性变换后空间定向不变（保持定向），行列式数值为变换的"缩放比例"（二维为单位面积缩放倍数，三维为单位体积缩放倍数）；
代数意义：矩阵 A A A 的列（或行）向量组线性无关，秩等于其维数，可逆，齐次线性方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 只有零解。

（3）当 det ⁡ ( A ) < 0 \det(A) < 0 det(A)<0 时

几何意义：线性变换后空间定向翻转（改变定向），行列式的绝对值为变换的"缩放比例"；
代数意义：矩阵 A A A 的列（或行）向量组线性无关，秩等于其维数，可逆，齐次线性方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 只有零解。

5.2 行列式符号的判断方法

二维空间 ：以标准基 e 1 = ( 1 0 ) \mathbf{e}_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} e1=(10)、 e 2 = ( 0 1 ) \mathbf{e}_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} e2=(01) 为参考，若变换后的 v 1 = A e 1 \mathbf{v}_1 = A\mathbf{e}_1 v1=Ae1 到 v 2 = A e 2 \mathbf{v}_2 = A\mathbf{e}_2 v2=Ae2 的最小旋转方向与 e 1 \mathbf{e}_1 e1 到 e 2 \mathbf{e}_2 e2 一致（如均为逆时针），则 det ⁡ ( A ) > 0 \det(A) > 0 det(A)>0，否则 det ⁡ ( A ) < 0 \det(A) < 0 det(A)<0；
三维空间 ：以标准基 e 1 = ( 1 0 0 ) \mathbf{e}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} e1= 100 、 e 2 = ( 0 1 0 ) \mathbf{e}_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} e2= 010 、 e 3 = ( 0 0 1 ) \mathbf{e}_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} e3= 001 为参考，用"右手定则"：食指指向 v 1 = A e 1 \mathbf{v}_1 = A\mathbf{e}_1 v1=Ae1、中指指向 v 2 = A e 2 \mathbf{v}_2 = A\mathbf{e}_2 v2=Ae2，若拇指指向与 v 3 = A e 3 \mathbf{v}_3 = A\mathbf{e}_3 v3=Ae3 一致，则 det ⁡ ( A ) > 0 \det(A) > 0 det(A)>0，否则 det ⁡ ( A ) < 0 \det(A) < 0 det(A)<0；

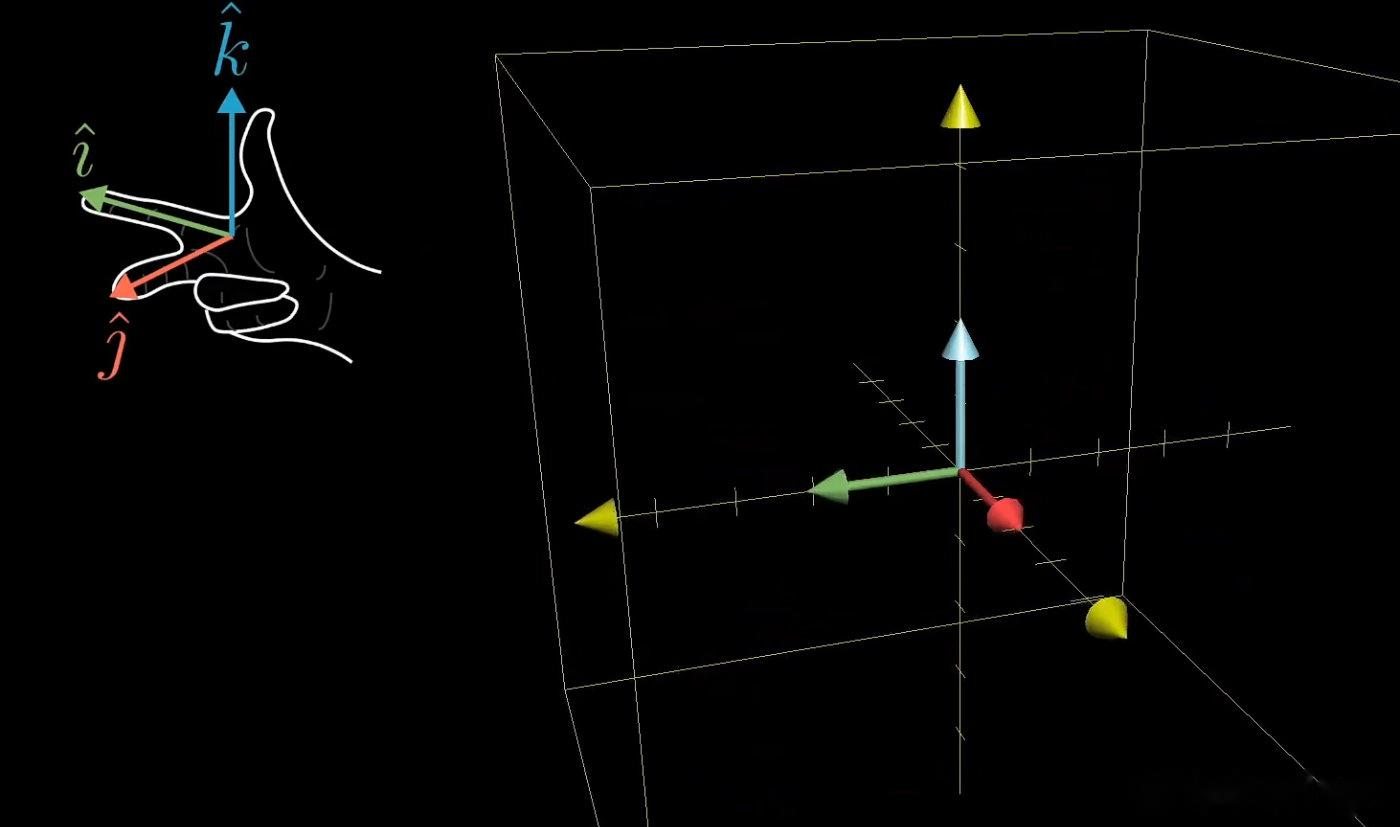
6. 基变换

在标准坐标系中，向量的坐标可理解为基向量 i ⃗ \vec{i} i 、 j ⃗ \vec{j} j 缩放的倍数。例如，向量 [ 3 2 ] \begin{bmatrix} 3 \\ 2 \end{bmatrix} [32] 表示将 i ⃗ \vec{i} i 缩放 3 3 3 倍、 j ⃗ \vec{j} j 缩放 2 2 2 倍后相加的结果。

基向量 i ⃗ \vec{i} i 、 j ⃗ \vec{j} j 是标准坐标系的隐含假设，向量与坐标之间的对应关系依赖于所选定的基，这种对应关系称为坐标系。

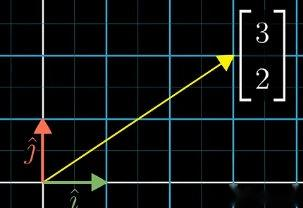
基变换描述向量在不同坐标系下的表示转换，关键逻辑如下：

6.1 基变换矩阵的定义

设标准基为 { e 1 , e 2 , ... , e n } \{\mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n\} {e1,e2,...,en}，新基为 { b 1 , b 2 , ... , b n } \{\mathbf{b}_1, \mathbf{b}_2, \dots, \mathbf{b}n\} {b1,b2,...,bn}，且新基在标准基下的表示为 b i = ∑ k = 1 n a k i e k \mathbf{b}i = \sum{k=1}^n a{ki}\mathbf{e}_k bi=∑k=1nakiek（ i = 1 , 2 , ... , n i=1,2,\dots,n i=1,2,...,n）。

构造矩阵 P = [ b 1 b 2 ... b n ] P = \begin{bmatrix} \mathbf{b}_1 & \mathbf{b}_2 & \dots & \mathbf{b}_n \end{bmatrix} P=[b1b2...bn]（列向量为新基在标准基下的表示），则 P P P 称为从新基到标准基的基变换矩阵。

6.2 向量在不同基下的表示转换

设向量 v \mathbf{v} v 在新基下的坐标为

x 1 x 2 ... x n \] \\begin{bmatrix} x_1 \\\\ x_2 \\\\ \\dots \\\\ x_n \\end{bmatrix} x1x2...xn ， 则 v = ∑ i = 1 n x i b i = P \[ x 1 x 2 ... x n \] \\mathbf{v} = \\sum_{i=1}\^n x_i \\mathbf{b}_i = P \\begin{bmatrix} x_1 \\\\ x_2 \\\\ \\dots \\\\ x_n \\end{bmatrix} v=∑i=1nxibi=P x1x2...xn 。 若 v \\mathbf{v} v 在标准基下的坐标为 \[ y 1 y 2 ... y n \] \\begin{bmatrix} y_1 \\\\ y_2 \\\\ \\dots \\\\ y_n \\end{bmatrix} y1y2...yn ， 则 \[ y 1 y 2 ... y n \] = P \[ x 1 x 2 ... x n \] \\begin{bmatrix} y_1 \\\\ y_2 \\\\ \\dots \\\\ y_n \\end{bmatrix} = P \\begin{bmatrix} x_1 \\\\ x_2 \\\\ \\dots \\\\ x_n \\end{bmatrix} y1y2...yn =P x1x2...xn ， 即新基坐标转换为标准基坐标的公式为 y = P x \\mathbf{y} = P\\mathbf{x} y=Px。 反之，标准基坐标转换为新基坐标的公式为 x = P − 1 y \\mathbf{x} = P\^{-1}\\mathbf{y} x=P−1y（ P − 1 P\^{-1} P−1 为 P P P 的逆矩阵）。 ##### 6.3 线性变换在不同基下的矩阵 设线性变换 L L L 在标准基下的矩阵为 M M M，在新基下的矩阵为 M ′ M' M′，则两者满足 M ′ = P − 1 M P M' = P\^{-1}MP M′=P−1MP，推导逻辑为： 1. 向量 v \\mathbf{v} v 在新基下的坐标为 x \\mathbf{x} x，转换为标准基坐标为 y = P x \\mathbf{y} = P\\mathbf{x} y=Px； 2. 标准基下执行变换 L L L： y ′ = M y = M P x \\mathbf{y}' = M\\mathbf{y} = MP\\mathbf{x} y′=My=MPx； 3. 转换回新基坐标： x ′ = P − 1 y ′ = P − 1 M P x \\mathbf{x}' = P\^{-1}\\mathbf{y}' = P\^{-1}MP\\mathbf{x} x′=P−1y′=P−1MPx； 4. 因此新基下变换矩阵为 M ′ = P − 1 M P M' = P\^{-1}MP M′=P−1MP。 ##### 6.4 基与坐标的关系示例 在标准坐标系中，向量的坐标可理解为基向量 i \\mathbf{i} i、 j \\mathbf{j} j 缩放的倍数。例如，向量 \[ 3 2 \] \\begin{bmatrix} 3 \\\\ 2 \\end{bmatrix} \[32\] 表示将 i \\mathbf{i} i 缩放 3 3 3 倍、 j \\mathbf{j} j 缩放 2 2 2 倍后相加的结果。基向量是标准坐标系的隐含假设，向量与坐标的对应关系依赖于选定的基。 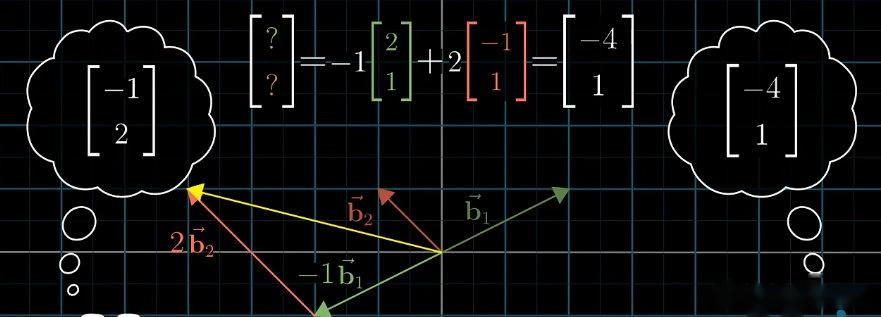![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/36683ce0d1a447a1add56089526ad612.png) 设存在"Jennifer 坐标系"，其基向量为 b 1 \\mathbf{b}_1 b1、 b 2 \\mathbf{b}_2 b2，在标准坐标系中表示为 b 1 = ( 2 , 1 ) \\mathbf{b}_1 = (2, 1) b1=(2,1)、 b 2 = ( − 1 , 1 ) \\mathbf{b}_2 = (-1, 1) b2=(−1,1)。则 Jennifer 坐标系中的任意向量 \[ x y \] \\begin{bmatrix} x \\\\ y \\end{bmatrix} \[xy\] 可表示为 x b 1 + y b 2 x\\mathbf{b}_1 + y\\mathbf{b}_2 xb1+yb2。 例如，Jennifer 坐标系中的向量 \[ − 1 2 \] \\begin{bmatrix} -1 \\\\ 2 \\end{bmatrix} \[−12\]，在标准坐标系中的表示为： − 1 ⋅ b 1 + 2 ⋅ b 2 = − 1 ⋅ ( 2 , 1 ) + 2 ⋅ ( − 1 , 1 ) = ( − 4 , 1 ) -1 \\cdot \\mathbf{b}_1 + 2 \\cdot \\mathbf{b}_2 = -1 \\cdot (2, 1) + 2 \\cdot (-1, 1) = (-4, 1) −1⋅b1+2⋅b2=−1⋅(2,1)+2⋅(−1,1)=(−4,1) 需注意：Jennifer 坐标系内部，基向量 b 1 \\mathbf{b}_1 b1、 b 2 \\mathbf{b}_2 b2 的坐标仍为 ( 1 , 0 ) (1, 0) (1,0)、 ( 0 , 1 ) (0, 1) (0,1)（所有坐标系的基向量在自身坐标系中均为标准单位向量）。 ##### 6.5 基变换矩阵的应用 将 Jennifer 坐标系的基向量在标准坐标系中的表示按列排列，构成矩阵 P = \[ 2 − 1 1 1 \] P = \\begin{bmatrix} 2 \& -1 \\\\ 1 \& 1 \\end{bmatrix} P=\[21−11\]，其作用是"Jennifer 坐标系坐标到标准坐标系坐标"的转换。例如，Jennifer 坐标系中的向量 \[ x y \] \\begin{bmatrix} x \\\\ y \\end{bmatrix} \[xy\]，在标准坐标系中的坐标为 P \[ x y \] P\\begin{bmatrix} x \\\\ y \\end{bmatrix} P\[xy\]。 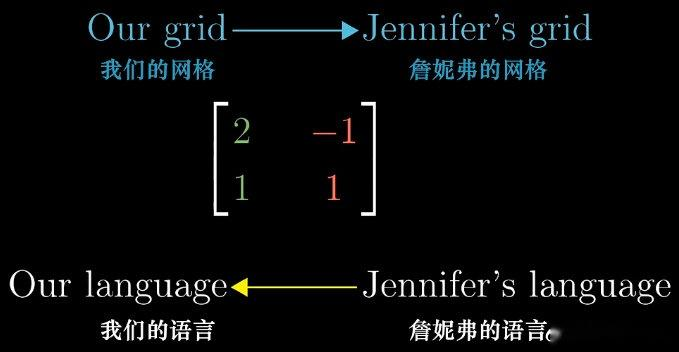![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/0fdb6ea8c42a4751825f44e3da469ee0.png) 矩阵 P P P 的逆矩阵 P − 1 P\^{-1} P−1 对应逆转换（标准坐标系到 Jennifer 坐标系）。例如，标准坐标系中的向量 \[ 3 2 \] \\begin{bmatrix} 3 \\\\ 2 \\end{bmatrix} \[32\]，在 Jennifer 坐标系中的坐标为： P − 1 \[ 3 2 \] = \[ 2 − 1 1 1 \] − 1 \[ 3 2 \] = \[ 1 3 1 3 − 1 3 2 3 \] \[ 3 2 \] = \[ 5 3 1 3 \] P\^{-1} \\begin{bmatrix} 3 \\\\ 2 \\end{bmatrix} = \\begin{bmatrix} 2 \& -1 \\\\ 1 \& 1 \\end{bmatrix}\^{-1} \\begin{bmatrix} 3 \\\\ 2 \\end{bmatrix} = \\begin{bmatrix} \\frac{1}{3} \& \\frac{1}{3} \\\\ -\\frac{1}{3} \& \\frac{2}{3} \\end{bmatrix} \\begin{bmatrix} 3 \\\\ 2 \\end{bmatrix} = \\begin{bmatrix} \\frac{5}{3} \\\\ \\frac{1}{3} \\end{bmatrix} P−1\[32\]=\[21−11\]−1\[32\]=\[31−313132\]\[32\]=\[3531

6.6 不同基下的线性变换示例

若需在 Jennifer 坐标系中实现"逆时针旋转 9 0 ∘ 90^\circ 90∘"，不能直接使用标准坐标系的旋转矩阵 [ 0 − 1 1 0 ] \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} [01−10]，需通过基变换实现，步骤为：

将 Jennifer 坐标系中的向量转换为标准坐标系坐标（乘以 P P P）；
在标准坐标系中进行逆时针 9 0 ∘ 90^\circ 90∘ 旋转（乘以旋转矩阵 R = [ 0 − 1 1 0 ] R = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} R=[01−10]）；
将旋转后的坐标转换回 Jennifer 坐标系（乘以 P − 1 P^{-1} P−1）。

最终，Jennifer 坐标系中逆时针旋转 9 0 ∘ 90^\circ 90∘ 的变换矩阵为 P − 1 R P P^{-1}RP P−1RP。一般地， P − 1 M P P^{-1}MP P−1MP 体现"坐标转移"思想： M M M 为标准坐标系的线性变换， P P P 与 P − 1 P^{-1} P−1 实现坐标转换， P − 1 M P P^{-1}MP P−1MP 为非标准坐标系中对应的线性变换。

三、线性方程组

1. 逆变换与逆矩阵

设线性变换 L L L 对应矩阵 A A A，若存在另一个线性变换 L − 1 L^{-1} L−1，使得对任意向量 v \mathbf{v} v，有 L − 1 ( L ( v ) ) = v L^{-1}(L(\mathbf{v})) = \mathbf{v} L−1(L(v))=v 且 L ( L − 1 ( v ) ) = v L(L^{-1}(\mathbf{v})) = \mathbf{v} L(L−1(v))=v，则称 L L L 为可逆变换， L − 1 L^{-1} L−1 为 L L L 的逆变换。

逆变换对应的矩阵称为原矩阵的逆矩阵，记为 A − 1 A^{-1} A−1，满足 A − 1 A = A A − 1 = I A^{-1}A = AA^{-1} = I A−1A=AA−1=I（ I I I 为单位矩阵，对应恒等变换）。

1.1 逆矩阵的存在性

矩阵 A A A 可逆的充要条件为 det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0（即 A A A 对应的变换为非降维变换）。若 det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0，则 A A A 对应的变换为降维变换（如二维平面压缩为直线），无法通过逆变换恢复原向量，因此 A A A 不可逆。

1.2 逆矩阵的示例

逆时针旋转 9 0 ∘ 90^\circ 90∘ 的变换矩阵为 A = [ 0 − 1 1 0 ] A = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} A=[01−10]，其逆变换为顺时针旋转 9 0 ∘ 90^\circ 90∘，对应的逆矩阵为 A − 1 = [ 0 1 − 1 0 ] A^{-1} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} A−1=[0−110]；
验证： A − 1 A = [ 0 1 − 1 0 ] [ 0 − 1 1 0 ] = [ 1 0 0 1 ] = I A^{-1}A = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I A−1A=[0−110][01−10]=[1001]=I；

2. 非齐次线性方程组的求解

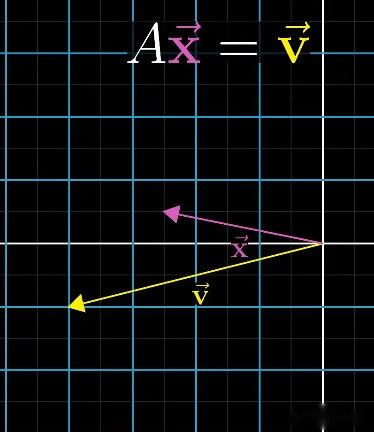
非齐次线性方程组的一般形式为 A x = v A \boldsymbol{x} = \boldsymbol{v} Ax=v，其中 A A A 为 m × n m \times n m×n 系数矩阵， x ∈ R n \boldsymbol{x} \in \mathbb{R}^n x∈Rn 为 n n n 维未知列向量， v ∈ R m \boldsymbol{v} \in \mathbb{R}^m v∈Rm 为 m m m 维非零常数列向量。求解的本质是"寻找向量 x \boldsymbol{x} x，使其经 A A A 对应的线性变换后与 v \boldsymbol{v} v 重合"。

2.1 基础定义与示例

给定方程组：
{ 2 x + 5 y + 3 z = − 3 4 x + 0 y + 8 z = 0 1 x + 3 y + 0 z = 2 \begin{cases} 2x + 5y + 3z = -3 \\ 4x + 0y + 8z = 0 \\ 1x + 3y + 0z = 2 \end{cases} ⎩ ⎨ ⎧2x+5y+3z=−34x+0y+8z=01x+3y+0z=2

其矩阵形式对应为：
A = [ 2 5 3 4 0 8 1 3 0 ] , x = [ x y z ] , v = [ − 3 0 2 ] A = \begin{bmatrix} 2 & 5 & 3 \\ 4 & 0 & 8 \\ 1 & 3 & 0 \end{bmatrix}, \quad \boldsymbol{x} = \begin{bmatrix} x \\ y \\ z \end{bmatrix}, \quad \boldsymbol{v} = \begin{bmatrix} -3 \\ 0 \\ 2 \end{bmatrix} A= 241503380 ,x= xyz ,v= −302

2.2 解的存在性与唯一性分析

解的情况需结合 A A A 的维度、秩（或行列式）及 v \boldsymbol{v} v 的位置判断，分为两类：

（1）当 A A A 为 n n n 阶方阵时

有唯一解（ det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0，即 A A A 满秩、可逆）
- 几何意义： A A A 对应 n n n 维空间到 n n n 维空间的非降维变换，仅存在一个 x \boldsymbol{x} x 经变换后与 v \boldsymbol{v} v 重合；
- 求解方法：对 A x = v A\boldsymbol{x} = \boldsymbol{v} Ax=v 两边左乘 A − 1 A^{-1} A−1，得唯一解 x = A − 1 v \boldsymbol{x} = A^{-1}\boldsymbol{v} x=A−1v（ v \boldsymbol{v} v 经 A A A 逆变换后的结果）。
无穷解或无解（ det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0，即 A A A 非满秩、不可逆）
- 几何意义： A A A 对应降维变换，变换后空间为 A A A 的列空间（维度小于 n n n），仅当 v \boldsymbol{v} v 落在列空间内时方程组有解；
- 解的个数：若 v \boldsymbol{v} v 在列空间内（即 v \boldsymbol{v} v 是 A A A 列向量的线性组合），则无穷多 x \boldsymbol{x} x 会被压缩到同一 v \boldsymbol{v} v，方程组有无穷解；若 v \boldsymbol{v} v 不在列空间内，则方程组无解。

（2）当 A A A 为非方阵时

解的存在性与唯一性需通过列空间维度、秩的关系（如 r ( A ) r(A) r(A) 与 r ( A ∣ v ) r(A|\boldsymbol{v}) r(A∣v) 是否相等）进一步分析，具体内容见"四、非方阵"章节。

3. 列空间

设 A A A 为 m × n m \times n m×n 矩阵， x ∈ R n \boldsymbol{x} \in \mathbb{R}^n x∈Rn，矩阵 A A A 的列空间（Column Space）定义为： A A A 的列向量所有线性组合构成的向量集合，本质是这些列向量张成的 R m \mathbb{R}^m Rm 子空间，也等价于所有形如 A x A\boldsymbol{x} Ax 的向量集合（线性变换 A A A 的所有可能输出），严格记为 Col ( A ) = { A x ∣ x ∈ R n } \text{Col}(A) = \{ A\boldsymbol{x} \mid \boldsymbol{x} \in \mathbb{R}^n \} Col(A)={Ax∣x∈Rn}。

3.1 列空间与秩的关系

矩阵 A A A 的秩（记为 R ( A ) R(A) R(A)）等于其列空间的维度，即 R ( A ) = dim ⁡ ( Col ( A ) ) R(A) = \dim(\text{Col}(A)) R(A)=dim(Col(A))。

例 1：若 3 × 3 3 \times 3 3×3 矩阵 A A A 的列空间为二维平面，则 R ( A ) = 2 R(A) = 2 R(A)=2；
例 2：若 3 × 3 3 \times 3 3×3 矩阵 A A A 的列空间为一维直线，则 R ( A ) = 1 R(A) = 1 R(A)=1。

3.2 列空间的性质

几何意义： Col ( A ) \text{Col}(A) Col(A) 是线性变换 A A A 作用后所有可能输出向量构成的空间；
零向量包含性：零向量 0 ∈ R m \boldsymbol{0} \in \mathbb{R}^m 0∈Rm 必在 Col ( A ) \text{Col}(A) Col(A) 内，因线性变换满足"保原点性"（ A 0 = 0 A\boldsymbol{0} = \boldsymbol{0} A0=0）；
方程组解的判定：非齐次线性方程组 A x = v A\boldsymbol{x} = \boldsymbol{v} Ax=v 有解的充要条件是 v ∈ Col ( A ) \boldsymbol{v} \in \text{Col}(A) v∈Col(A)。

4. 零空间与齐次线性方程组

4.1 概念与定义

零空间（Null Space），记作 N ( A ) N(A) N(A) 或 ker ( A ) \text{ker}(A) ker(A)，是矩阵 A A A 变换后所有落在零向量上的向量集合，本质是齐次线性方程组 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 的所有解的集合，定义为：
N ( A ) = { x ⃗ ∣ A x ⃗ = 0 ⃗ } N(A) = \left\{ \vec{x} \mid A\vec{x} = \vec{0} \right\} N(A)={x ∣Ax =0 }

非满秩变换（不可逆变换） ：当 A A A 不可逆（ det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0，或列/行向量线性相关，或秩小于维度）时，空间被压缩至更低维度，除零向量外，还存在非零向量 x ⃗ \vec{x} x 经 A A A 变换后变为零向量，零空间即这些向量的集合；
齐次方程解 ：零空间直接给出 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 的所有可能解。

4.2 零空间与解的关系

当 det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0 时 ： A A A 可逆（满秩），零空间仅包含零向量（ N ( A ) = { 0 ⃗ } N(A) = \{\vec{0}\} N(A)={0 }），齐次方程 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 只有唯一零解 x ⃗ = 0 ⃗ \vec{x} = \vec{0} x =0 ；
当 det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0 时 ： A A A 不可逆（不满秩），零空间包含非零向量，齐次方程 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 有非零解（无穷多解），这些解构成零空间。

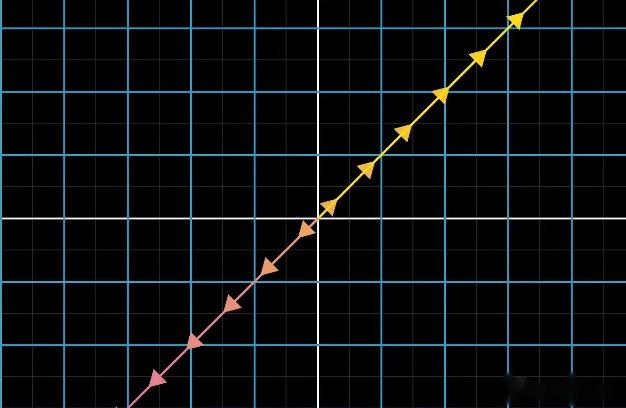
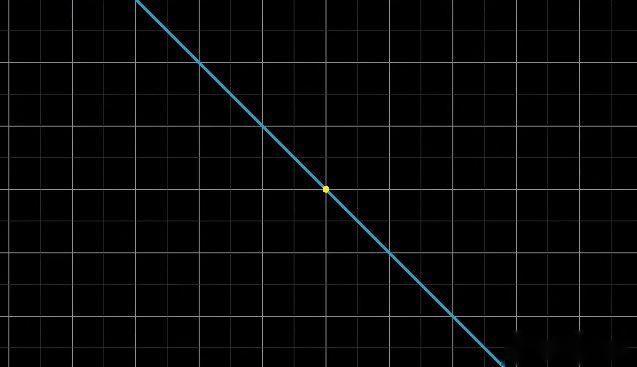
下方示意图展示非满秩变换如何将一条直线（零空间中的向量集合，若零空间为一维）压缩为单个点（零向量）：


变换前的向量集合	变换后变为零向量的集合

4.3 方程组求解的实质

无论是 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 （齐次）还是 A x ⃗ = b ⃗ A\vec{x} = \vec{b} Ax =b （非齐次， b ⃗ ≠ 0 ⃗ \vec{b} \neq \vec{0} b =0 ），求解本质是在定义域 R n \mathbb{R}^n Rn 中寻找向量 x ⃗ \vec{x} x ，使其经 A A A 的线性变换后满足特定条件：

齐次方程组 ：寻找所有 x ⃗ ∈ R n \vec{x} \in \mathbb{R}^n x ∈Rn，使 A x ⃗ A\vec{x} Ax 等于零向量（即找到 N ( A ) N(A) N(A) 中的所有向量）；
非齐次方程组 ：寻找所有 x ⃗ ∈ R n \vec{x} \in \mathbb{R}^n x ∈Rn，使 A x ⃗ A\vec{x} Ax 等于目标向量 b ⃗ \vec{b} b （即判断 b ⃗ \vec{b} b 是否在 Col ( A ) \text{Col}(A) Col(A) 内，若在则找到所有映射到 b ⃗ \vec{b} b 的"原像" x ⃗ \vec{x} x ）。

零空间 N ( A ) N(A) N(A) 在理解非齐次方程组的通解结构（特解加上齐次方程组的通解）中起关键作用。

四、非方阵

此前讨论的线性变换均为等维变换（输入与输出向量维度相同），非方阵（行数与列数不相等）可实现向量维度的升高或降低，对应维度映射型线性变换。

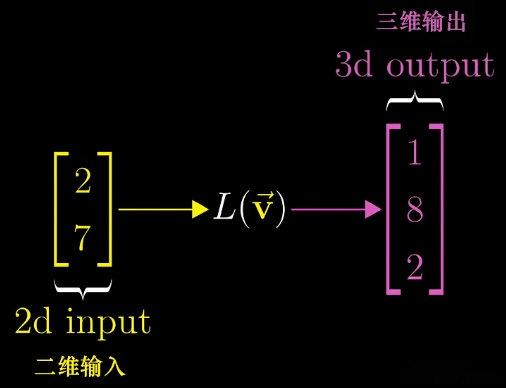
1. 非方阵变换矩阵的实质

与方阵类似，非方阵的列向量可看作线性变换后基向量的形式，含义由矩阵的行数（ m m m）与列数（ n n n）决定：

m × n m \times n m×n 非方阵的列向量，对应 n n n 维原始空间基向量经变换后的结果，且变换后基向量用 m m m 个坐标表示（属于 m m m 维空间）；
因此， m × n m \times n m×n 非方阵对应的线性变换，是将 n n n 维向量转换为 m m m 维向量。

示例：

3 × 2 3 \times 2 3×2 矩阵 [ 1 2 3 4 5 6 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} 135246 ：列向量为二维基向量 i \mathbf{i} i、 j \mathbf{j} j 经变换后的三维向量，对应"二维到三维"的升维变换；
2 × 3 2 \times 3 2×3 矩阵 [ 1 2 3 4 5 6 ] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} [142536]：列向量为三维基向量 i \mathbf{i} i、 j \mathbf{j} j、 k \mathbf{k} k 经变换后的二维向量，对应"三维到二维"的降维变换；
1 × n 1 \times n 1×n 矩阵：对应" n n n 维向量到一维标量"的映射； n × 1 n \times 1 n×1 矩阵：对应"一维标量到 n n n 维向量"的映射（如向量数乘）。

需注意向量数乘与非方阵变换的区别：

向量数乘：仅对向量进行缩放，不改变方向（除非乘负数）和维度，可看作特殊的方阵变换（对角矩阵）；
非方阵变换：核心功能是改变向量的维度（升维或降维）；
方阵变换：不改变向量维度，仅进行旋转、缩放、剪切、反射等几何操作。

2. 几何意义

非方阵对应的线性变换本质是"向量在不同维度空间间的映射"，具体示例如下：

3 × 2 3 \times 2 3×2 矩阵 [ 1 2 3 4 5 6 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} 135246 ：列空间为两个三维列向量张成的二维平面，向量乘法 [ 1 2 3 4 5 6 ] [ 1 4 ] \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 4 \end{bmatrix} 135246 [14] 的几何意义是"将二维向量映射到三维空间的该二维平面上"；
2 × 3 2 \times 3 2×3 矩阵 [ 1 2 3 4 5 6 ] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} [142536]：列空间为三个二维列向量张成的二维平面，向量乘法 [ 1 2 3 4 5 6 ] [ 1 3 5 ] \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 3 \\ 5 \end{bmatrix} [142536] 135 的几何意义是"将三维向量映射到该二维平面上"；
1 × 2 1 \times 2 1×2 矩阵 [ 1 4 ] \begin{bmatrix} 1 & 4 \end{bmatrix} [14]：列空间为两个一维向量张成的一维直线，向量乘法 [ 1 4 ] [ 1 4 ] \begin{bmatrix} 1 & 4 \end{bmatrix} \begin{bmatrix} 1 \\ 4 \end{bmatrix} [14][14] 的几何意义是"将二维向量映射到该一维直线上，结果为标量"；
2 × 1 2 \times 1 2×1 矩阵 [ 1 4 ] \begin{bmatrix} 1 \\ 4 \end{bmatrix} [14]：列空间为该二维向量张成的一维直线，向量乘法 [ 1 4 ] × 4 \begin{bmatrix} 1 \\ 4 \end{bmatrix} \times 4 [14]×4 的几何意义是"将一维标量映射到该一维直线上"。

3. 非方阵的变换类型

3.1 行数大于列数（ m > n m > n m>n）：升维操作

以 3 × 2 3 \times 2 3×2 矩阵 A = [ a b c d e f ] A = \begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix} A= acebdf 为例，其线性变换将二维向量 x ⃗ = [ m n ] \vec{x} = \begin{bmatrix} m \\ n \end{bmatrix} x =[mn] 转换为三维向量 v ⃗ = [ x y z ] \vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} v = xyz （即 A x ⃗ = v ⃗ A\vec{x} = \vec{v} Ax =v ），实现升维。

该变换的列空间为矩阵 A A A 两列（三维向量）张成的二维平面，与原始向量维度相同，因此 A A A 为满秩矩阵（秩等于列数 n = 2 n = 2 n=2）。

3.2 行数小于列数（ m < n m < n m<n）：降维操作

以 2 × 3 2 \times 3 2×3 矩阵 B = [ p q r s t u ] B = \begin{bmatrix} p & q & r \\ s & t & u \end{bmatrix} B=[psqtru] 为例，其线性变换将三维向量 v ⃗ = [ x y z ] \vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} v = xyz 转换为二维向量 x ⃗ = [ m n ] \vec{x} = \begin{bmatrix} m \\ n \end{bmatrix} x =[mn]（即 B v ⃗ = x ⃗ B\vec{v} = \vec{x} Bv =x ），实现降维。

该变换的列空间为矩阵 B B B 三列（二维向量）张成的二维平面，小于原始向量维度（ 3 3 3），因此 B B B 为非满秩矩阵（秩等于行数 m = 2 m = 2 m=2）。

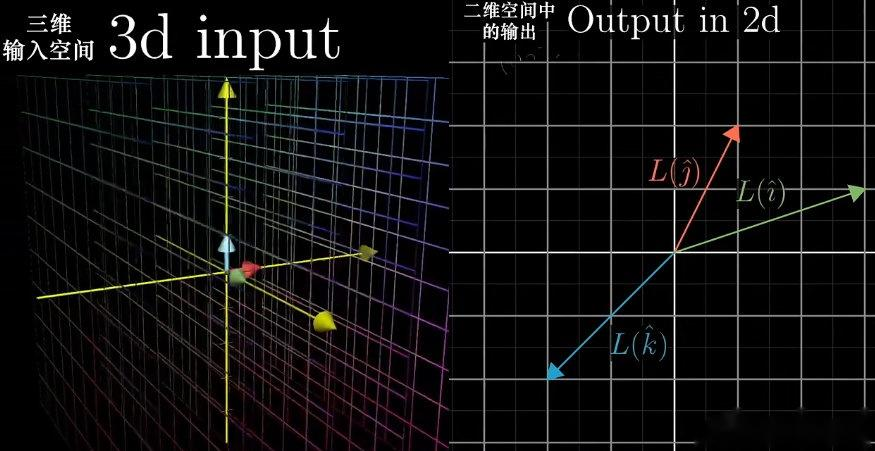
4. 非方阵的变换复合

非方阵矩阵相乘需满足"左矩阵列数 = 右矩阵行数"，复合变换结果由矩阵顺序决定，核心差异为信息是否损失。

设 3 × 2 3 \times 2 3×2 满秩矩阵 A = [ a b c d e f ] A = \begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix} A= acebdf ， 2 × 3 2 \times 3 2×3 满秩矩阵 B = [ g h i j k l ] B = \begin{bmatrix} g & h & i \\ j & k & l \end{bmatrix} B=[gjhkil]，二维向量 x ⃗ = [ m n ] \vec{x} = \begin{bmatrix} m \\ n \end{bmatrix} x =[mn]，三维向量 v ⃗ = [ x y z ] \vec{v} = \begin{bmatrix} x \\ y \\ z \end{bmatrix} v = xyz ，两类复合变换对比如下：

4.1 复合变换 B A BA BA（先 A A A 后 B B B）

变换顺序 ：以二维向量 x ⃗ \vec{x} x 为初始，先经 A A A 映射，再经 B B B 映射；
分步过程 ： x ⃗ \vec{x} x （二维）→ A x ⃗ A\vec{x} Ax （三维，落在 A A A 的列空间）→ B A x ⃗ BA\vec{x} BAx （二维，落在 B B B 的列空间）；
信息状态 ：全程保持二维范围映射，无信息丢失，原始向量 x ⃗ \vec{x} x 可通过逆变换还原；
矩阵属性 ： B A BA BA 为 2 × 2 2 \times 2 2×2 方阵，列空间维度为 2 2 2（满秩），具备可逆性。

4.2 复合变换 A B AB AB（先 B B B 后 A A A）

变换顺序 ：以三维向量 v ⃗ \vec{v} v 为初始，先经 B B B 映射，再经 A A A 映射；
分步过程 ： v ⃗ \vec{v} v （三维）→ B v ⃗ B\vec{v} Bv （二维，落在 B B B 的列空间，伴随三维压缩）→ A B v ⃗ AB\vec{v} ABv （三维，落在 A A A 的列空间）；
信息状态 ：初始三维空间被压缩至二维，信息不可逆失，原始向量 v ⃗ \vec{v} v 无法还原；
矩阵属性 ： A B AB AB 为 3 × 3 3 \times 3 3×3 方阵，列空间维度为 2 2 2（非满秩），不具备可逆性。

5. 非方阵系数矩阵的线性方程组

5.1 基本概念与几何本质

以非方阵 A A A 为系数矩阵的线性方程组分为两类：

非齐次线性方程组 A x ⃗ = v ⃗ A\vec{x} = \vec{v} Ax =v ：寻找向量 x ⃗ \vec{x} x ，使经 A A A 变换后与 v ⃗ \vec{v} v 重合；
齐次线性方程组 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 ：寻找向量 x ⃗ \vec{x} x ，使经 A A A 变换后得到零向量 0 ⃗ \vec{0} 0 。

从几何视角看，求解本质是"在 A A A 的列空间中，寻找与 v ⃗ \vec{v} v 重合的向量（非齐次），或寻找能映射为零向量的向量（齐次）"。

5.2 行数大于列数的满秩矩阵（ m × n m \times n m×n， m > n m > n m>n）

设 A A A 为 m × n m \times n m×n 列满秩矩阵（满秩条件 R ( A ) = n R(A) = n R(A)=n，列向量线性无关），其列空间为 m m m 维空间中的 n n n 维子空间（如 3 × 2 3 \times 2 3×2 满秩矩阵的列空间是三维空间内的二维平面）。

5.2.1 非齐次方程组 A x ⃗ = v ⃗ A\vec{x} = \vec{v} Ax =v 的解

存在性 ：当且仅当 v ⃗ \vec{v} v 属于 A A A 的列空间时，方程组有解（此时增广矩阵秩 R ( [ A ∣ v ⃗ ] ) = R ( A ) = n R([A|\vec{v}]) = R(A) = n R([A∣v ])=R(A)=n）；若 v ⃗ \vec{v} v 不在列空间内， R ( [ A ∣ v ⃗ ] ) = n + 1 > R ( A ) R([A|\vec{v}]) = n + 1 > R(A) R([A∣v ])=n+1>R(A)，方程组无解；
唯一性 ：有解时，因列向量线性无关， x ⃗ \vec{x} x 的每个分量由线性组合唯一确定，解唯一。

5.2.2 齐次方程组 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 的解

因列向量线性无关，仅当线性组合系数全为零时，列向量组合才能得到零向量，故方程组仅有零解（无中生有）。

5.3 行数小于列数的满秩矩阵（ m × n m \times n m×n， m < n m < n m<n）

设 A A A 为 m × n m \times n m×n 行满秩矩阵（满秩条件 R ( A ) = m R(A) = m R(A)=m，行向量线性无关），其列空间为完整的 m m m 维空间（因行满秩时列空间维度等于行数 m m m）。

5.3.1 非齐次方程组 A x ⃗ = v ⃗ A\vec{x} = \vec{v} Ax =v 的解

存在性 ：因 v ⃗ \vec{v} v 是 m m m 维向量，必然属于 A A A 的列空间（列空间为完整 m m m 维空间），故方程组总有解（ R ( [ A ∣ v ⃗ ] ) = R ( A ) = m R([A|\vec{v}]) = R(A) = m R([A∣v ])=R(A)=m，无矛盾行）；
解的数量 ：自由变量个数为 n − R ( A ) = n − m > 0 n - R(A) = n - m > 0 n−R(A)=n−m>0，自由变量取不同值对应不同解，故方程组有无穷多解。

5.3.2 齐次方程组 A x ⃗ = 0 ⃗ A\vec{x} = \vec{0} Ax =0 的解

因解空间维度为 n − R ( A ) = n − m > 0 n - R(A) = n - m > 0 n−R(A)=n−m>0，存在非零向量满足方程，故方程组有非零解（即存在向量经 A A A 变换后被压缩为零向量）。

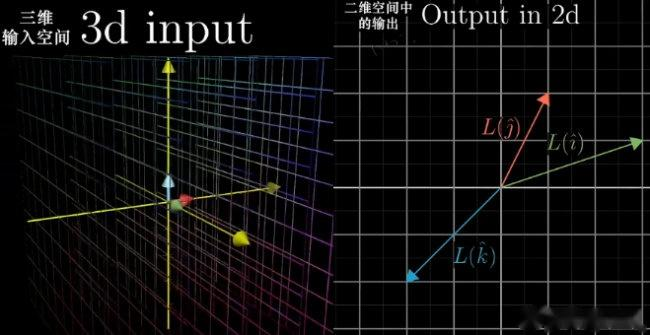
5.4 解的情况总结与验证

非方阵方程组 A x ⃗ = v ⃗ A\vec{x} = \vec{v} Ax =v 解的存在性与唯一性，取决于 A A A 的维度（ m m m 与 n n n 的大小）和秩，具体总结如下表：

矩阵类型	满秩条件	解的情况
m × n m \times n m×n（ m > n m > n m>n）	R ( A ) = n R(A) = n R(A)=n（列满秩）	非齐次： v ⃗ \vec{v} v 在列空间内则有唯一解，否则无解齐次：仅零解
m × n m \times n m×n（ m < n m < n m<n）	R ( A ) = m R(A) = m R(A)=m（行满秩）	非齐次：总有解，且有无穷多解齐次：有非零解

5.4.1 列满秩矩阵（ m > n m > n m>n）的验证

满秩条件 ： R ( A ) = n R(A) = n R(A)=n 表示列向量线性无关，列空间维度等于列数 n n n；
解的验证 ：存在性由 v ⃗ \vec{v} v 是否在列空间决定，唯一性由列向量线性无关保证，齐次方程仅零解。

5.4.2 行满秩矩阵（ m < n m < n m<n）的验证

满秩条件 ： R ( A ) = m R(A) = m R(A)=m 表示行向量线性无关，行空间维度等于行数 m m m；
解的验证 ：存在性由列空间覆盖完整 m m m 维空间保证，无穷多解由自由变量个数大于 0 0 0 保证，齐次方程有非零解由解空间维度大于 0 0 0 保证。

线性代数 | 要义 / 本质（增篇 2）-CSDN博客
https://blog.csdn.net/u013669912/article/details/153657084

线性代数 | 要义 / 本质（上篇）-CSDN博客
https://blog.csdn.net/u013669912/article/details/153110982
线性代数 | 要义 / 本质（下篇）_行列式的定义-CSDN博客
https://blog.csdn.net/u013669912/article/details/153215664

via: 重排自

线性代数的本质（完整版） - 知乎
https://zhuanlan.zhihu.com/p/629986822