线性代数 | 要义 / 本质（下篇）

注：本文为 "线性代数 | 要义 / 本质" 相关合辑。

略排未全校，如有内容异常，请看原文。

线性代数 | 要义 / 本质（上篇）-CSDN博客
https://blog.csdn.net/u013669912/article/details/153110982

【直观详解】线性代数的本质（下篇）

5 行列式的几何意义

The purpose of computation is insight, not numbers - Richard Hamming

计算的目的不在于数字本身，而在于洞察其背后的意义 ------理查德·汉明（没错，是发明汉明码的那个人）

5.1 行列式的定义

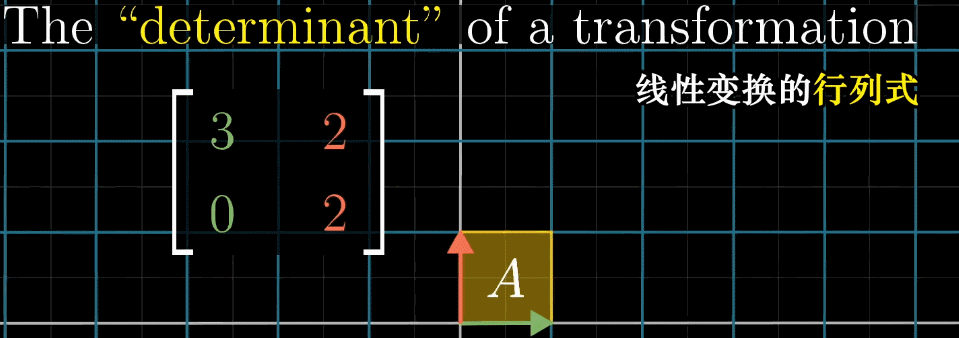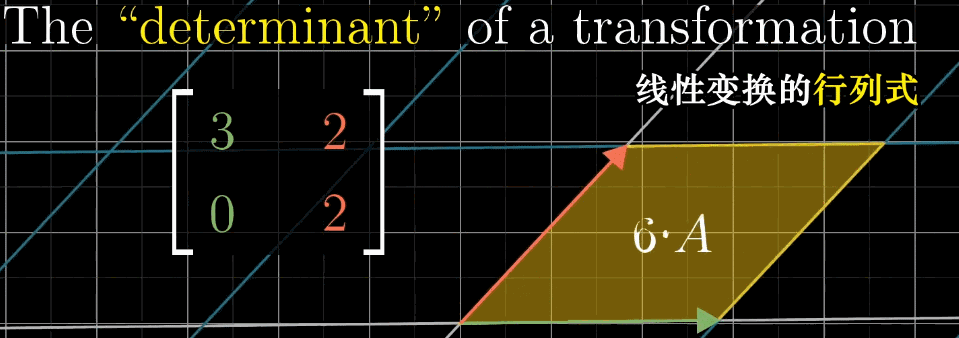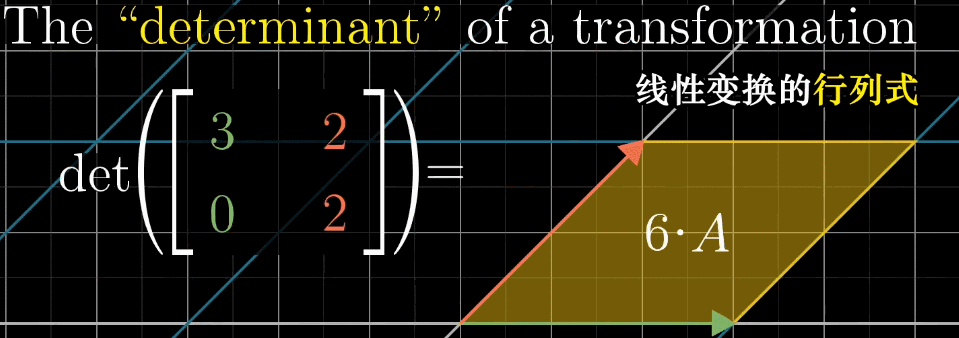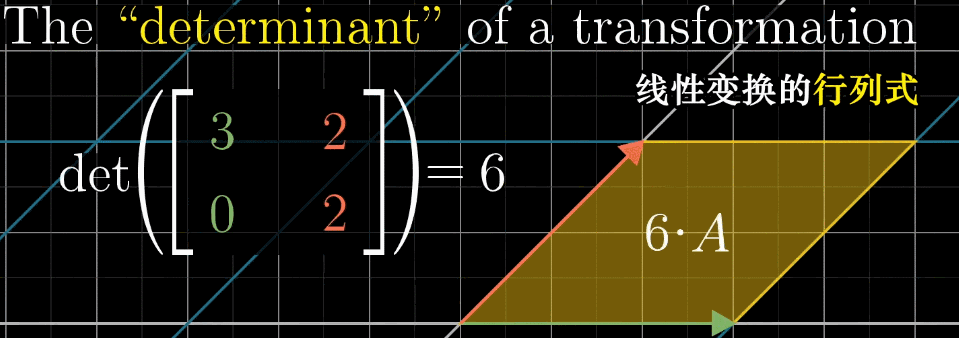
行列式是衡量线性变换对空间体积（面积 / 体积）缩放比例 的指标，记为 det ⁡ ( A ) \det (A) det(A) 或 ∣ A ∣ |A| ∣A∣。

二维空间：对于矩阵 A = [ a b c d ] A = \begin {bmatrix} a & b \\ c & d \end {bmatrix} A=[acbd]，其行列式为 det ⁡ ( A ) = a d − b c \det (A) = ad - bc det(A)=ad−bc，几何意义是 "标准基 { ı ^ , ȷ ^ } \{\hat {\imath}, \hat {\jmath}\} {^,^} 构成的单位正方形，经 A A A 变换后形成的平行四边形的面积"；
三维空间：对于矩阵 A = [ a b c d e f g h i ] A = \begin {bmatrix} a & b & c \\ d & e & f \\ g & h & i \end {bmatrix} A= adgbehcfi ，其行列式为 det ⁡ ( A ) = a ( e i − f h ) − b ( d i − f g ) + c ( d h − e g ) \det (A) = a (ei - fh) - b (di - fg) + c (dh - eg) det(A)=a(ei−fh)−b(di−fg)+c(dh−eg)，几何意义是 "标准基 { ı ^ , ȷ ^ , k ^ } \{\hat {\imath}, \hat {\jmath}, \hat {k}\} {^,^,k^} 构成的单位立方体，经 A A A 变换后形成的平行六面体的体积"。

5.2 行列式的符号与降维

5.2.1 行列式的符号意义

行列式的正负表示线性变换是否改变空间的"定向"，具体判断方式随空间维度不同而变化：

二维空间 ：以单位向量 ı ^ \hat{\imath} ^ 为参照，若 ȷ ^ \hat{\jmath} ^ 经变换后从 ı ^ \hat{\imath} ^ 的左侧转移至右侧（效果类似"纸的翻面"），则行列式为负；反之， ȷ ^ \hat{\jmath} ^ 相对 ı ^ \hat{\imath} ^ 方位不变，行列式为正。
三维空间 ：空间定向通过右手定则判断------右手四指沿 ı ^ → ȷ ^ → k ^ \hat{\imath} \to \hat{\jmath} \to \hat{k} ^→^→k^ 顺序弯曲，大拇指指向为空间正定向。变换后定向方向相反，行列式为负；定向方向不变，行列式为正。

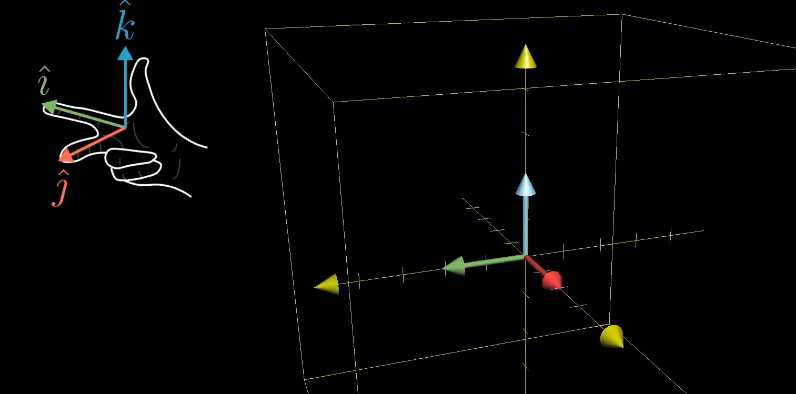
5.2.2 行列式与空间降维的关系

若矩阵 A A A 的行列式 det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0，则该矩阵对应的线性变换会导致空间维度降低：

二维空间变换后降为直线；
三维空间变换后降为平面或直线。

其本质是： det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0 时，矩阵 A A A 的列向量线性相关，张成的空间维度小于矩阵阶数（如二阶矩阵列向量张成一维空间，三阶矩阵列向量张成二维或一维空间）。

5.2.3 线性变换的性质与行列式的作用

线性变换的基本性质 ：

线性变换保持图形的平行性，但改变图形的大小与方向；且不必然保持形状------仅旋转、反射等特殊线性变换保形，剪切变换等会改变图形形状。
行列式在二维线性变换中的作用 ：

行列式是描述矩阵缩放作用的标量值，可确定二维线性变换的两个关键结果：
- 判断朝向变化 ：行列式为正，图形朝向不变；行列式为负，图形朝向反转。
- 确定面积缩放比例 ：行列式的绝对值等于面积缩放比例。绝对值为 1 时面积不变，大于 1 时面积放大，小于 1 时面积缩小。

5.3 行列式的重要性质

由几何意义可直接推导行列式的核心性质：

det ⁡ ( M 1 M 2 ) = det ⁡ ( M 1 ) det ⁡ ( M 2 ) \det (M_1M_2) = \det (M_1)\det (M_2) det(M1M2)=det(M1)det(M2)：复合变换的体积缩放比例等于各变换缩放比例的乘积；
det ⁡ ( A − 1 ) = 1 det ⁡ ( A ) \det (A^{-1}) = \frac {1}{\det (A)} det(A−1)=det(A)1：逆变换的缩放比例是原变换的倒数（若原变换放大 k k k 倍，逆变换缩小 1 k \frac {1}{k} k1 倍）；
det ⁡ ( k A ) = k n det ⁡ ( A ) \det (kA) = k^n\det (A) det(kA)=kndet(A)： n n n 阶矩阵的数乘变换，体积缩放比例为 k n k^n kn（二维：面积缩放 k 2 k^2 k2，三维：体积缩放 k 3 k^3 k3）。

行列式直观理解

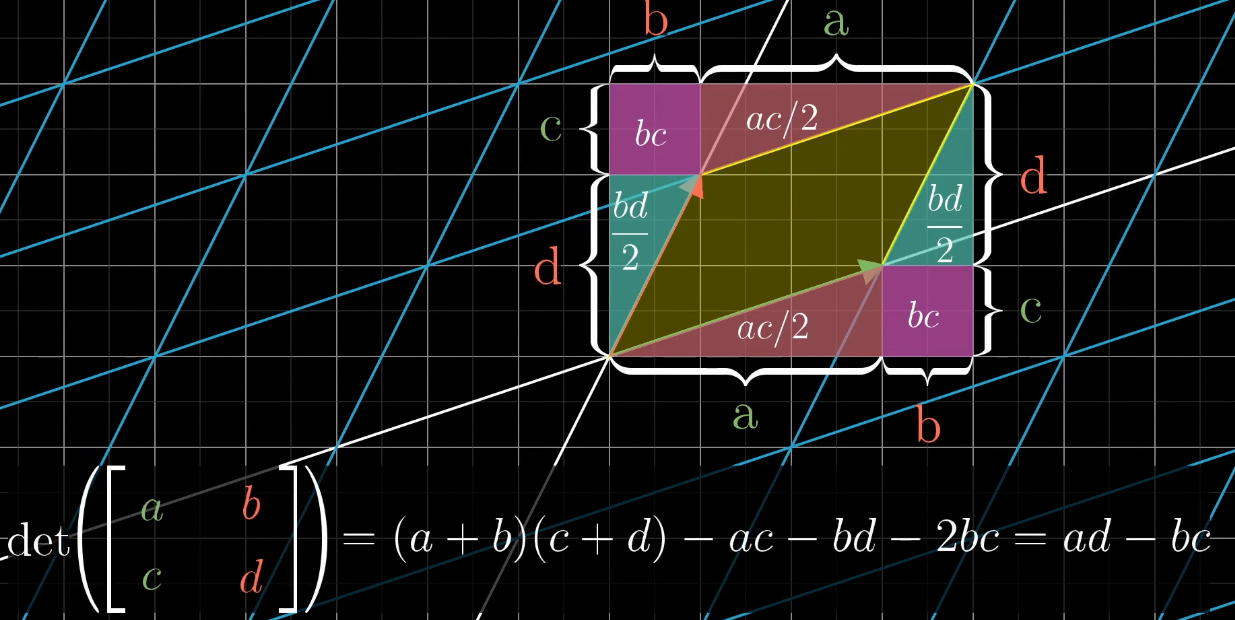
行列式是矩阵的一个数值特征，为建立行列式计算公式与几何直观的联系，二阶矩阵 [ a b c d ] \begin{bmatrix} a&b\\ c&d\end{bmatrix} [acbd] 的行列式，对应其列向量张成图形的有向面积：

当 b = c = 0 b = c = 0 b=c=0 时，矩阵为 [ a 0 0 d ] \begin{bmatrix} a&0\\ 0&d\end{bmatrix} [a00d]， a a a 是 i ^ \hat{i} i^ 在 x x x 轴的缩放比例， d d d 是 j ^ \hat{j} j^ 在 y y y 轴的缩放比例，行列式 a d ad ad 是单位正方形按 a a a、 d d d 拉伸后的面积（拉伸倍数）。
当 b b b、 c c c 非 0 0 0 时，行列式 a d − b c ad - bc ad−bc 综合了 x x x、 y y y 轴拉伸与图形"倾斜压缩"的效果，为变换后图形的有向面积（总缩放比例）。

6 逆矩阵、列空间与零空间

To ask the right question is harder than to answer it - Georg Cantor

提出正确的问题比回答它更难 ------格奥尔格·康托尔

6.1 线性方程组的几何意义

线性方程组的一般形式为 A x ⃗ = v ⃗ A\vec {x} = \vec {v} Ax =v ，其中 A A A 为 n × n n \times n n×n 矩阵， x ⃗ \vec {x} x 为待求向量，

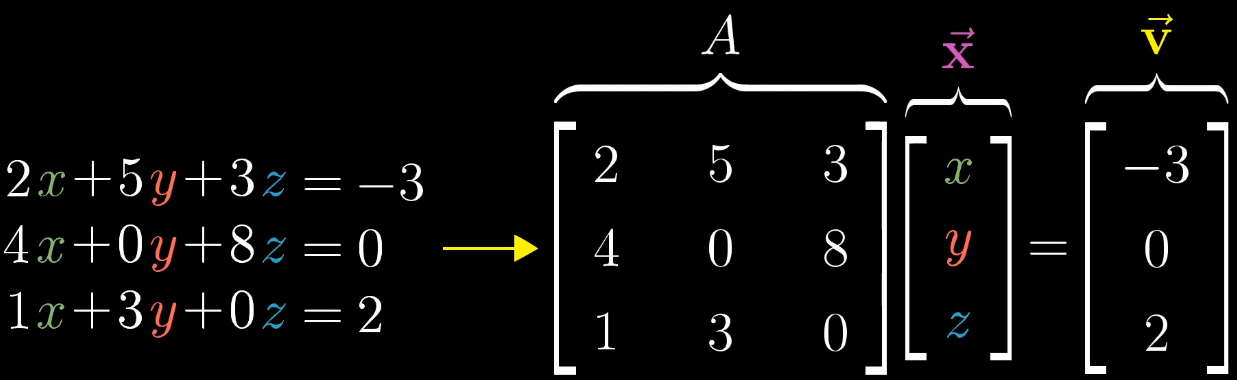
几何直观来翻译个公式即 A x ⃗ A\vec {x} Ax 经过 A A A 矩阵变换后，恰好落在 v ⃗ \vec {v} v 上

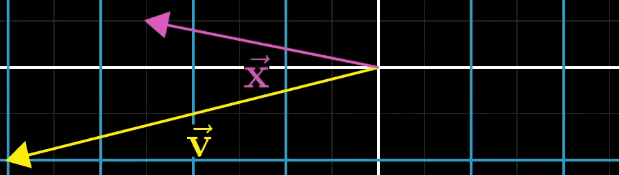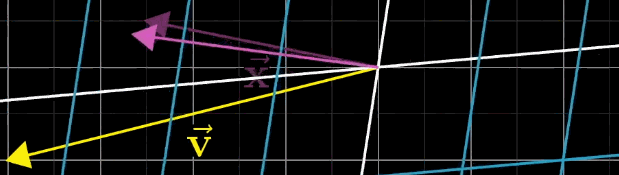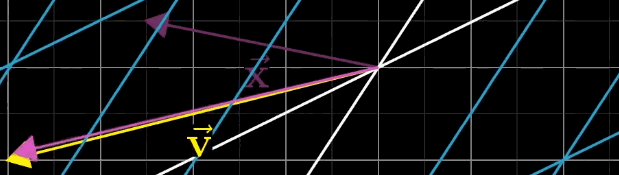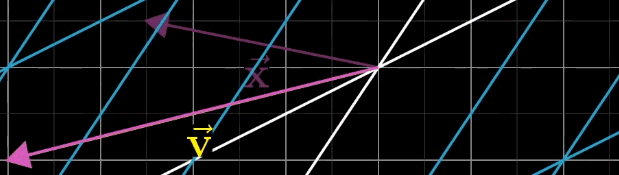
从线性变换的角度，该方程的几何意义是：找到向量 x ⃗ \vec {x} x ，使其经 A A A 变换后恰好等于 v ⃗ \vec {v} v。

6.2 逆矩阵与方程组求解

6.2.1 逆矩阵的定义

若存在矩阵 A − 1 A^{-1} A−1，使得 A − 1 A = I A^{-1} A = I A−1A=I（ I I I 为单位矩阵， I = [ 1 0 0 1 ] I = \begin {bmatrix} 1 & 0 \\ 0 & 1 \end {bmatrix} I=[1001]（二维）， I = [ 1 0 0 0 1 0 0 0 1 ] I = \begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end {bmatrix} I= 100010001 （三维）），则称 A − 1 A^{-1} A−1 为 A A A 的逆矩阵。

几何意义： A − 1 A^{-1} A−1 对应的变换是 A A A 的 "逆操作"------ 若 A A A 将 x ⃗ \vec {x} x 变换为 v ⃗ \vec {v} v ，则 A − 1 A^{-1} A−1 将 v ⃗ \vec {v} v 变换回 x ⃗ \vec {x} x 。

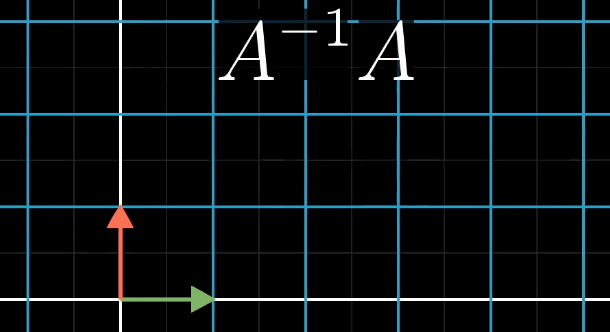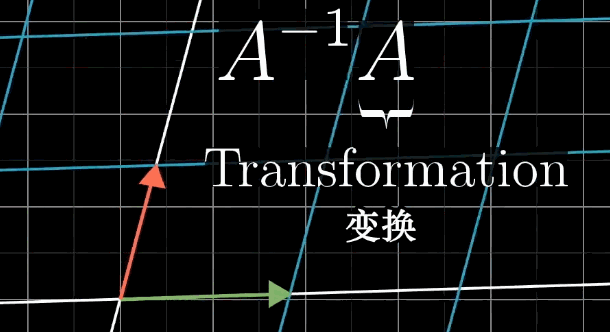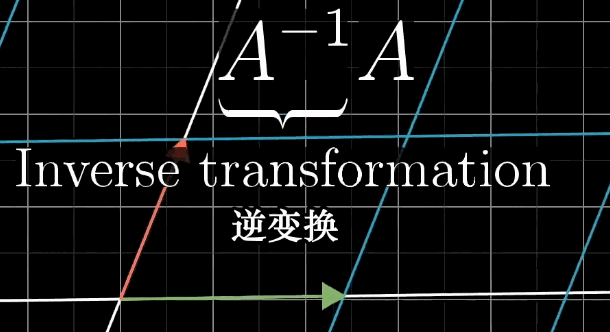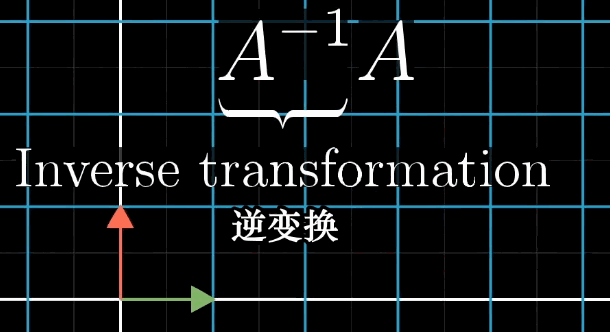
6.2.2 线性方程组的解

在线性代数中，任意一个 m × n m \times n m×n 型线性方程组均可以表示为矩阵形式 A x = v A\mathbf{x} = \mathbf{v} Ax=v，其中各符号的定义如下：

A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n：称为系数矩阵，由方程组中未知量的系数按原顺序构成；
x ∈ R n \mathbf{x} \in \mathbb{R}^n x∈Rn：称为未知向量，包含方程组中所有待求解的未知量；
v ∈ R m \mathbf{v} \in \mathbb{R}^m v∈Rm：称为常数项向量，由方程组等号右侧的常数项构成。

该矩阵形式的核心意义在于：线性方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 与从向量空间 R n \mathbb{R}^n Rn 到 R m \mathbb{R}^m Rm 的线性变换 T A : R n → R m T_A: \mathbb{R}^n \to \mathbb{R}^m TA:Rn→Rm（定义为 T A ( x ) = A x T_A(\mathbf{x}) = A\mathbf{x} TA(x)=Ax）一一对应。这种对应关系将"求解方程组"转化为"分析线性变换的性质"，我们可从逆变换、列空间、零空间三个维度，系统讨论方程组解的存在性、唯一性及解集合的结构。

1. 逆变换与方程组的唯一解

当线性变换 T A T_A TA 满足"可逆"条件时，方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 存在唯一解，具体推导与结论如下：

1.1 可逆的等价条件

线性变换 T A T_A TA 可逆，等价于其对应的系数矩阵 A A A 满足两个条件：

A A A 是方阵（即 m = n m = n m=n，方程组的"方程个数"等于"未知量个数"）；
A A A 的行列式非零 （即 det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0，此时 A A A 称为可逆矩阵或非奇异矩阵）。

行列式非零的几何意义是：线性变换 T A T_A TA 不会导致向量空间"降维"（例如， R 3 \mathbb{R}^3 R3 中的变换不会将向量映射到 R 2 \mathbb{R}^2 R2 或更低维的空间），因此每个输出向量 v \mathbf{v} v 都能唯一对应一个输入向量 x \mathbf{x} x。

1.2 唯一解的代数形式

若 A A A 可逆，则其逆矩阵 A − 1 A^{-1} A−1 存在且唯一（满足 A − 1 A = A A − 1 = I A^{-1}A = AA^{-1} = I A−1A=AA−1=I，其中 I I I 为单位矩阵）。对 A x = v A\mathbf{x} = \mathbf{v} Ax=v 两边同时左乘 A − 1 A^{-1} A−1，可通过矩阵运算直接求解 x \mathbf{x} x：
A − 1 A x = A − 1 v ⟹ I x = A − 1 v ⟹ x = A − 1 v A^{-1}A\mathbf{x} = A^{-1}\mathbf{v} \implies I\mathbf{x} = A^{-1}\mathbf{v} \implies \mathbf{x} = A^{-1}\mathbf{v} A−1Ax=A−1v⟹Ix=A−1v⟹x=A−1v

从线性变换的角度看，该解等价于"将逆变换 T A − 1 T_A^{-1} TA−1 作用于 v \mathbf{v} v"，即 x = T A − 1 ( v ) \mathbf{x} = T_A^{-1}(\mathbf{v}) x=TA−1(v)，这进一步印证了解的唯一性------逆变换的输出是唯一的。

2. 列空间与方程组的解的存在性

当 T A T_A TA 不可逆（或 A A A 非方阵）时，方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 未必有解，需通过系数矩阵 A A A 的列空间（Column Space）判定解的存在性。

2.1 列空间的定义

系数矩阵 A A A 的列空间（记为 Col ( A ) \text{Col}(A) Col(A)）是 A A A 的所有列向量在 R m \mathbb{R}^m Rm 中通过"线性组合"张成的子空间。例如，若 A = [ a 1 a 2 ... a n ] A = [\mathbf{a}_1\ \mathbf{a}_2\ \dots\ \mathbf{a}_n] A=[a1 a2 ... an]（其中 a i ∈ R m \mathbf{a}_i \in \mathbb{R}^m ai∈Rm 是 A A A 的第 i i i 列），则：
Col ( A ) = { c 1 a 1 + c 2 a 2 + ⋯ + c n a n ∣ c 1 , c 2 , ... , c n ∈ R } \text{Col}(A) = \left\{ c_1\mathbf{a}_1 + c_2\mathbf{a}_2 + \dots + c_n\mathbf{a}_n \mid c_1, c_2, \dots, c_n \in \mathbb{R} \right\} Col(A)={c1a1+c2a2+⋯+cnan∣c1,c2,...,cn∈R}

其几何意义是：线性变换 T A T_A TA 的所有可能输出向量 构成的集合，即 T A T_A TA 的"值域"。

2.2 解的存在性充要条件

根据列空间的定义，方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解的本质是" v \mathbf{v} v 属于 T A T_A TA 的值域"，因此可得到核心结论：

线性方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解的充要条件 是：常数项向量 v \mathbf{v} v 属于系数矩阵 A A A 的列空间，即 v ∈ Col ( A ) \mathbf{v} \in \text{Col}(A) v∈Col(A)。

结合行列式的特殊情况（当 A A A 为方阵时）：

若 det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0（ A A A 可逆），则 Col ( A ) = R m \text{Col}(A) = \mathbb{R}^m Col(A)=Rm（列空间充满整个目标空间），因此对任意 v ∈ R m \mathbf{v} \in \mathbb{R}^m v∈Rm，方程组均有解（与第1节结论一致）；
若 det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0（ A A A 不可逆），则 Col ( A ) \text{Col}(A) Col(A) 是 R m \mathbb{R}^m Rm 的真子空间（维度低于 m m m），此时仅当 v \mathbf{v} v 落在该真子空间内时，方程组有解，否则无解。

3. 零空间与方程组的解集合结构

当方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解时，解的个数可能是"唯一"或"无穷多"，需通过系数矩阵 A A A 的零空间（Null Space）刻画解集合的完整结构。

3.1 零空间的定义

系数矩阵 A A A 的零空间（记为 Nul ( A ) \text{Nul}(A) Nul(A)）是齐次线性方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0（常数项向量全为0的方程组）的所有解向量在 R n \mathbb{R}^n Rn 中构成的子空间，即：
Nul ( A ) = { z ∈ R n ∣ A z = 0 } \text{Nul}(A) = \left\{ \mathbf{z} \in \mathbb{R}^n \mid A\mathbf{z} = \mathbf{0} \right\} Nul(A)={z∈Rn∣Az=0}

齐次方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 始终有解（至少存在零解 x = 0 \mathbf{x} = \mathbf{0} x=0），因此零空间 Nul ( A ) \text{Nul}(A) Nul(A) 永远非空。

3.2 解集合的结构定理

设非齐次方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v 有解，且 x 0 \mathbf{x}_0 x0 是其任意一个特解（即满足 A x 0 = v A\mathbf{x}_0 = \mathbf{v} Ax0=v 的某个固定解），则方程组的所有解 可表示为"特解 + 零空间中任意向量"的形式，即：
x = x 0 + z , 其中 z ∈ Nul ( A ) \mathbf{x} = \mathbf{x}_0 + \mathbf{z}, \quad \text{其中 } \mathbf{z} \in \text{Nul}(A) x=x0+z,其中 z∈Nul(A)

该定理的逻辑验证如下：

解的有效性 ：若 z ∈ Nul ( A ) \mathbf{z} \in \text{Nul}(A) z∈Nul(A)，则 A z = 0 A\mathbf{z} = \mathbf{0} Az=0，因此 A ( x 0 + z ) = A x 0 + A z = v + 0 = v A(\mathbf{x}_0 + \mathbf{z}) = A\mathbf{x}_0 + A\mathbf{z} = \mathbf{v} + \mathbf{0} = \mathbf{v} A(x0+z)=Ax0+Az=v+0=v，即 x 0 + z \mathbf{x}_0 + \mathbf{z} x0+z 是方程组的解；
解的完整性 ：设 x \mathbf{x} x 是方程组的任意一个解，则 A ( x − x 0 ) = A x − A x 0 = v − v = 0 A(\mathbf{x} - \mathbf{x}_0) = A\mathbf{x} - A\mathbf{x}_0 = \mathbf{v} - \mathbf{v} = \mathbf{0} A(x−x0)=Ax−Ax0=v−v=0，即 x − z ∈ Nul ( A ) \mathbf{x} - \mathbf{z} \in \text{Nul}(A) x−z∈Nul(A)，因此 x \mathbf{x} x 可表示为 x 0 + ( x − x 0 ) \mathbf{x}_0 + (\mathbf{x} - \mathbf{x}_0) x0+(x−x0)，符合上述形式。

3.3 特殊情况的解集合

根据上述定理，可进一步明确两类典型方程组的解集合：

非齐次方程组 A x = v A\mathbf{x} = \mathbf{v} Ax=v ：
- 若 v ∉ Col ( A ) \mathbf{v} \notin \text{Col}(A) v∈/Col(A)：解集合为空集（无解）；
- 若 v ∈ Col ( A ) \mathbf{v} \in \text{Col}(A) v∈Col(A)：解集合为 { x 0 + z ∣ z ∈ Nul ( A ) } \left\{ \mathbf{x}_0 + \mathbf{z} \mid \mathbf{z} \in \text{Nul}(A) \right\} {x0+z∣z∈Nul(A)}（无穷多解，除非 Nul ( A ) = { 0 } \text{Nul}(A) = \left\{ \mathbf{0} \right\} Nul(A)={0}，即零空间仅含零向量，此时解唯一）。
齐次方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 ：
- 特解 x 0 = 0 \mathbf{x}_0 = \mathbf{0} x0=0（零解），因此解集合就是零空间 Nul ( A ) \text{Nul}(A) Nul(A)；
- 若 Nul ( A ) = { 0 } \text{Nul}(A) = \left\{ \mathbf{0} \right\} Nul(A)={0}，则仅有零解；若 Nul ( A ) \text{Nul}(A) Nul(A) 维度大于0，则有无穷多非零解。

6.3 列空间（Column Space）

矩阵 A A A 的列空间 是其所有列向量张成的空间，记为 C ( A ) C (A) C(A)。

几何意义：列空间是线性变换 A A A 的 "所有可能输出向量" 的集合（即 A x ⃗ A\vec {x} Ax 的所有可能结果）；
维度与秩：列空间的维度称为矩阵的秩（记为 rank ( A ) \text {rank}(A) rank(A)）。对于 n × n n \times n n×n 矩阵，若 rank ( A ) = n \text {rank}(A) = n rank(A)=n（满秩），则列空间是整个 n n n 维空间；若 rank ( A ) < n \text {rank}(A) < n rank(A)<n（降秩），则列空间是 n n n 维空间的一个子空间（如二维中的直线、三维中的平面）。

重要性质 ：零向量 0 ⃗ \vec {0} 0 一定在列空间中（令 x ⃗ = 0 ⃗ \vec {x} = \vec {0} x =0 ，则 A 0 ⃗ = 0 ⃗ A\vec {0} = \vec {0} A0 =0 ）。

6.4 零空间（Null Space）

所有经过该矩阵变换后落在原点的向量的集合，称为该矩阵（再次强调，矩阵是变换的数字表达）的零空间或核。

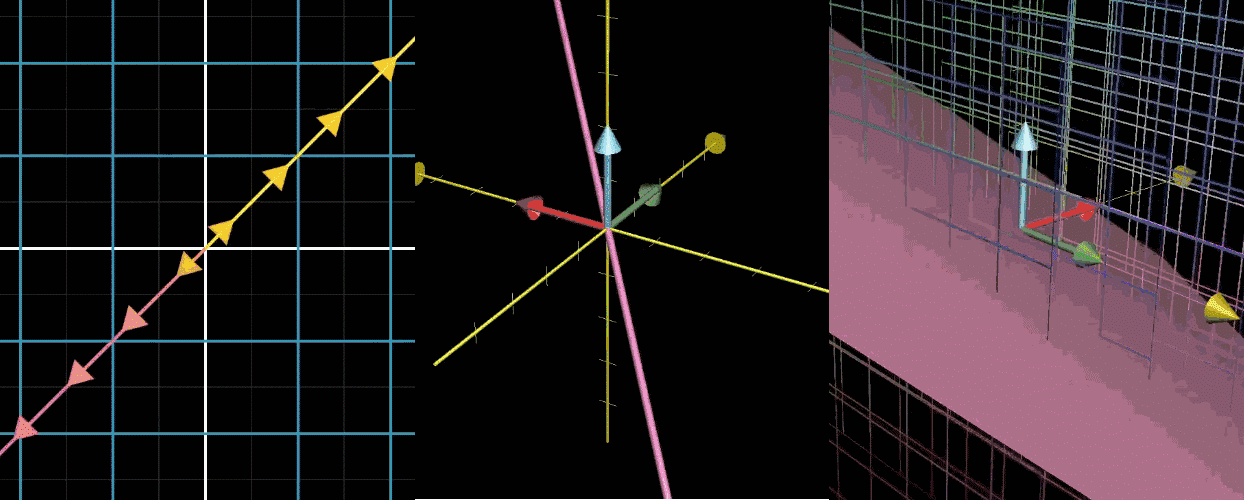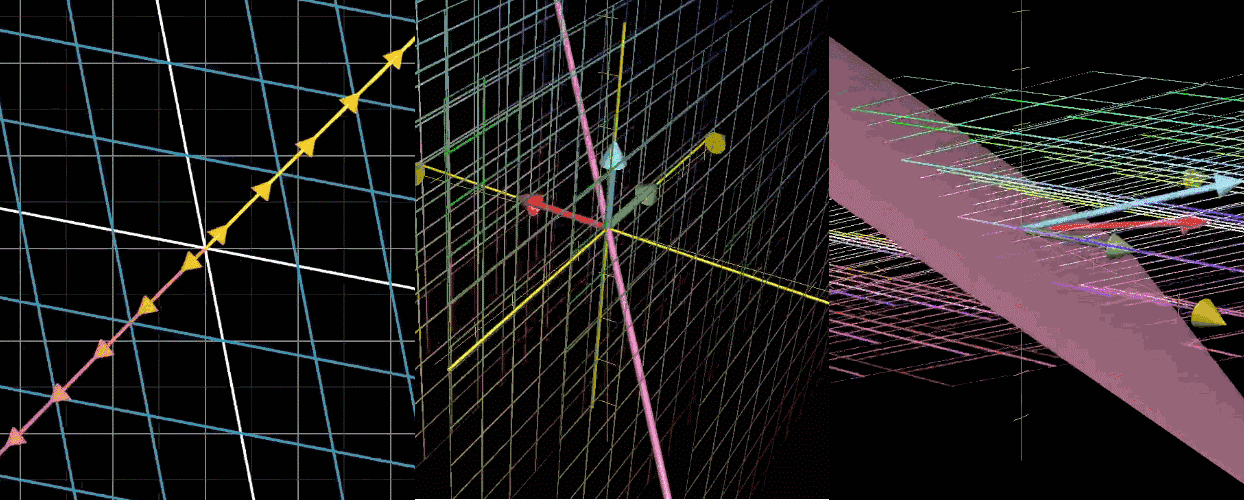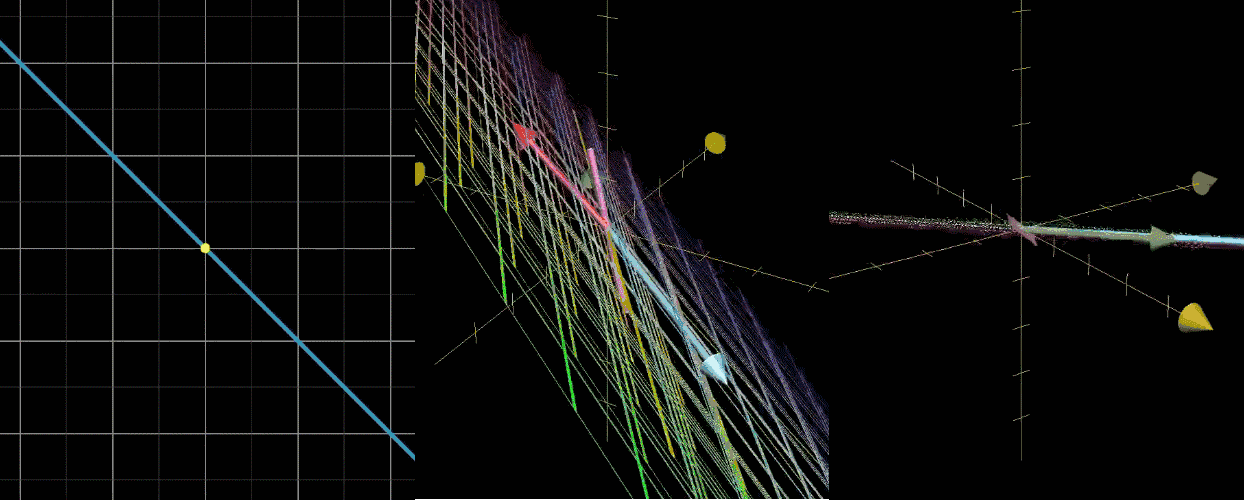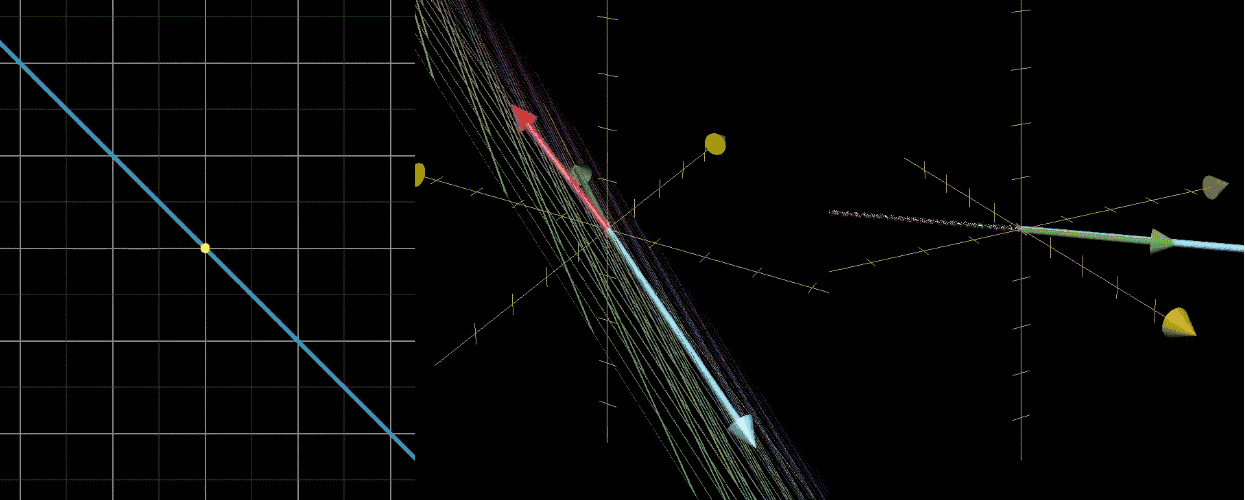
图 1 二维空间压缩到一条直线（一维），其中一条直线（一维）上的点被压缩到原点。
图 2 三维空间压缩到一个平面（二维），其中一条直线（一维）上的点被压缩到原点。
图 3 三维空间压缩到一条直线（一维），其中一个平面（二维）上的点被压缩到原点。
注意：线性压缩是一种线性变换，而矩阵是线性变换在给定基下的代数表示（数字表达），二者一一对应但并非等同。

矩阵 A A A 的零空间 是满足 A x ⃗ = 0 ⃗ A\vec {x} = \vec {0} Ax =0 的所有向量 x ⃗ \vec {x} x 的集合，记为 N ( A ) N (A) N(A)。

几何意义：零空间是线性变换 A A A 中 "被压缩到原点的向量" 的集合；
维度关系（秩 - 零定理）：对于 n × n n \times n n×n 矩阵， rank ( A ) + dim ⁡ ( N ( A ) ) = n \text {rank}(A) + \dim (N (A)) = n rank(A)+dim(N(A))=n（列空间维度与零空间维度之和等于矩阵的阶数）。

示例：

若 A A A 是 2 × 2 2 \times 2 2×2 矩阵且 det ⁡ ( A ) = 0 \det (A) = 0 det(A)=0（二维→一维），则零空间是一条直线（所有被压缩到原点的向量构成的直线）；
若 A A A 是 3 × 3 3 \times 3 3×3 矩阵且 rank ( A ) = 2 \text {rank}(A) = 2 rank(A)=2（三维→二维），则零空间是一条直线（ dim ⁡ ( N ( A ) ) = 3 − 2 = 1 \dim (N (A)) = 3 - 2 = 1 dim(N(A))=3−2=1）。

6.4.1 秩-零化度定理

零化度（Nullity）是线性代数中矩阵零空间的维数，是衡量矩阵"将向量映射为零向量"能力的重要指标。

零空间（Null Space，又称核空间 Kernel）：指矩阵 A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n 的所有解向量 x ∈ R n \mathbf{x} \in \mathbb{R}^n x∈Rn 的集合，即 N ( A ) = { x ∈ R n ∣ A x = 0 } \text{N}(A) = \{\mathbf{x} \in \mathbb{R}^n \mid A\mathbf{x} = \mathbf{0}\} N(A)={x∈Rn∣Ax=0}。
零化度的本质：零空间作为一个向量空间，其维数即为零化度（记为 nullity ( A ) \text{nullity}(A) nullity(A)），等价于零空间中"极大线性无关组的向量个数"（即零空间的基向量数）。
零化度的计算：通过对矩阵 A A A 做初等行变换化为行最简形，解线性方程组 A x = 0 A\mathbf{x} = \mathbf{0} Ax=0 得到自由变量的个数，该个数即为零化度（自由变量数 = 零空间维数）。

对任意 m × n m \times n m×n 矩阵 A A A，其列空间的维数 （即秩 rank ( A ) \text{rank}(A) rank(A)）与零空间的维数 （零化度）之和，等于矩阵的列数 n n n，即：

dim ⁡ ( Col ( A ) ) + dim ⁡ ( Nul ( A ) ) = n \dim(\text{Col}(A)) + \dim(\text{Nul}(A)) = n dim(Col(A))+dim(Nul(A))=n

注意：是"维数之和"，而非"空间本身相加"------列空间（ R m \mathbb{R}^m Rm 子空间）与零空间（ R n \mathbb{R}^n Rn 子空间）维度可能不同，无法直接叠加。

6.4.2 满秩与列空间、零空间

"满秩"是矩阵的属性（ rank ( A ) = min ⁡ ( m , n ) \text{rank}(A) = \min(m, n) rank(A)=min(m,n)），结合上述定理分析：

若 A A A 为 n × n n \times n n×n 方阵（满秩即 rank ( A ) = n \text{rank}(A) = n rank(A)=n）：
由定理得 dim ⁡ ( Nul ( A ) ) = 0 \dim(\text{Nul}(A)) = 0 dim(Nul(A))=0（零空间仅含零向量），且列空间 Col ( A ) = R n \text{Col}(A) = \mathbb{R}^n Col(A)=Rn（满维子空间）。
若 A A A 为长方阵（如 m < n m < n m<n 时满秩即 rank ( A ) = m \text{rank}(A) = m rank(A)=m）：
列空间 Col ( A ) = R m \text{Col}(A) = \mathbb{R}^m Col(A)=Rm（满维），零空间维数 n − m > 0 n - m > 0 n−m>0（含非零解）。

7 非方阵的几何意义

On this quiz, I asked you to find the determinant of a 2*3 matrix. Some of you, to my great amusement, actually tried to do this - no name listed

在这个小测试里，我让你们求一个 2*3 矩阵的行列式。让我感到非常可笑的是，你们当中竟然有人尝试去做 ------佚名

7.1 非方阵的维度映射

非方阵（如 m × n m \times n m×n 矩阵， m ≠ n m \neq n m=n）对应的线性变换是不同维度空间之间的映射：

m × n m \times n m×n 矩阵：将 n n n 维输入空间映射到 m m m 维输出空间；
示例： 3 × 2 3 \times 2 3×2 矩阵将二维空间映射到三维空间（输入为 2 2 2 维向量，输出为 3 3 3 维向量），其列向量是二维标准基 { ı ^ , ȷ ^ } \{\hat {\imath}, \hat {\jmath}\} {^,^} 在三维空间中的变换结果。

7.2 非方阵乘法的条件

两个非方阵 M 1 M_1 M1（ p × q p \times q p×q）与 M 2 M_2 M2（ q × r q \times r q×r）可相乘的充要条件是：前一个矩阵的列数等于后一个矩阵的行数 （即 M 1 M_1 M1 的输入维度等于 M 2 M_2 M2 的输出维度），乘积矩阵 M = M 1 M 2 M = M_1M_2 M=M1M2 的维度为 p × r p \times r p×r。

几何意义： M 2 M_2 M2 将 r r r 维空间映射到 q q q 维空间， M 1 M_1 M1 再将 q q q 维空间映射到 p p p 维空间，复合变换的输入维度为 r r r，输出维度为 p p p，与乘积矩阵维度一致。

7.3 非方阵的行列式

非方阵不存在行列式，因为行列式的核心是 "体积缩放比例"，而不同维度空间之间的映射（如二维→三维）无法定义 "体积比"（二维空间的 "面积" 与三维空间的 "体积" 单位不同，无直接比例关系）。

8 点积与对偶性

卡尔文：你知道吗，我觉数学不是一门科学，而是一种宗教。

霍布斯：一种宗教？

卡尔文：是啊。这些公式就像奇迹一般。你取出两个数，把它们相加时，它们神奇地成为了一个全新的数！没人能说清这到底是怎么发生的。你要么完全相信，要么完全不信。

8.1 点积的定义与几何意义

8.1.1 代数定义

对于 n n n 维向量 v ⃗ = [ v 1 v 2 ⋯ v n ] \vec {v} = \begin {bmatrix} v_1 \\ v_2 \\ \cdots \\ v_n \end {bmatrix} v = v1v2⋯vn 与 w ⃗ = [ w 1 w 2 ⋯ w n ] \vec {w} = \begin {bmatrix} w_1 \\ w_2 \\ \cdots \\ w_n \end {bmatrix} w = w1w2⋯wn ，其点积为：
v ⃗ ⋅ w ⃗ = v 1 w 1 + v 2 w 2 + ⋯ + v n w n \vec {v} \cdot \vec {w} = v_1w_1 + v_2w_2 + \cdots + v_nw_n v ⋅w =v1w1+v2w2+⋯+vnwn

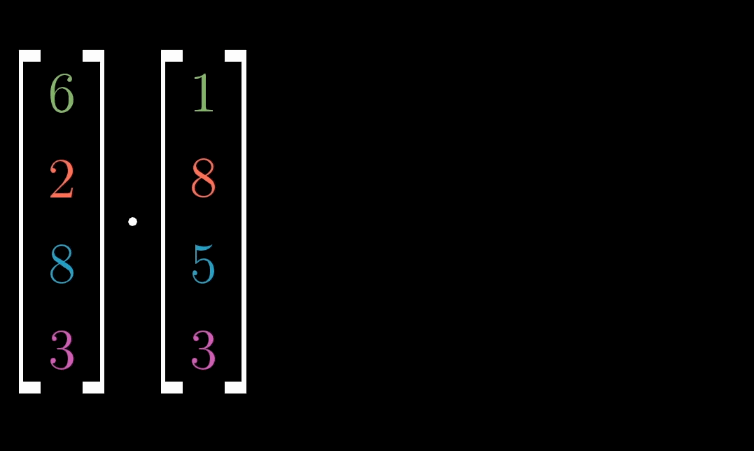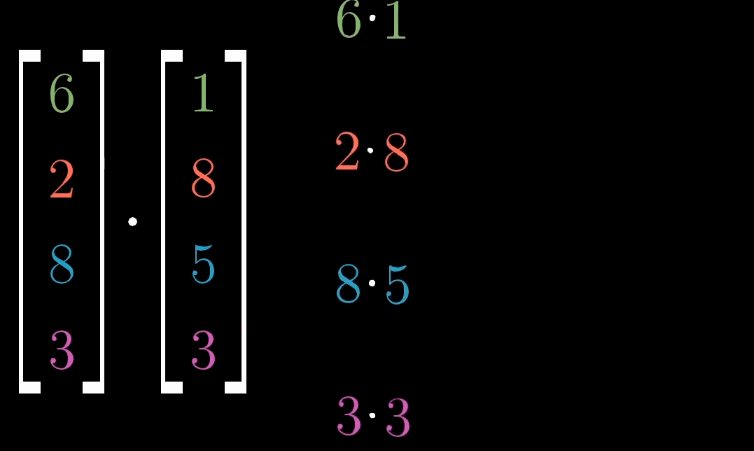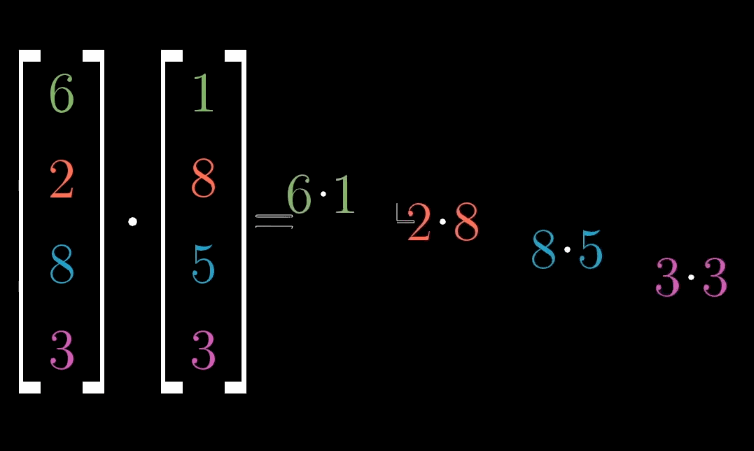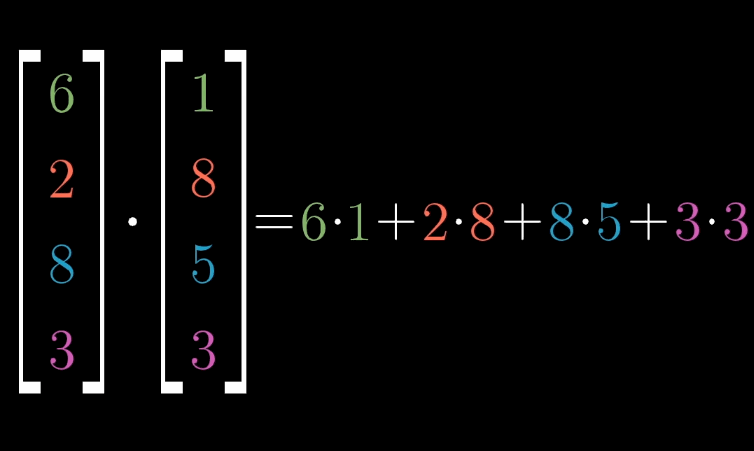
8.1.2 几何意义

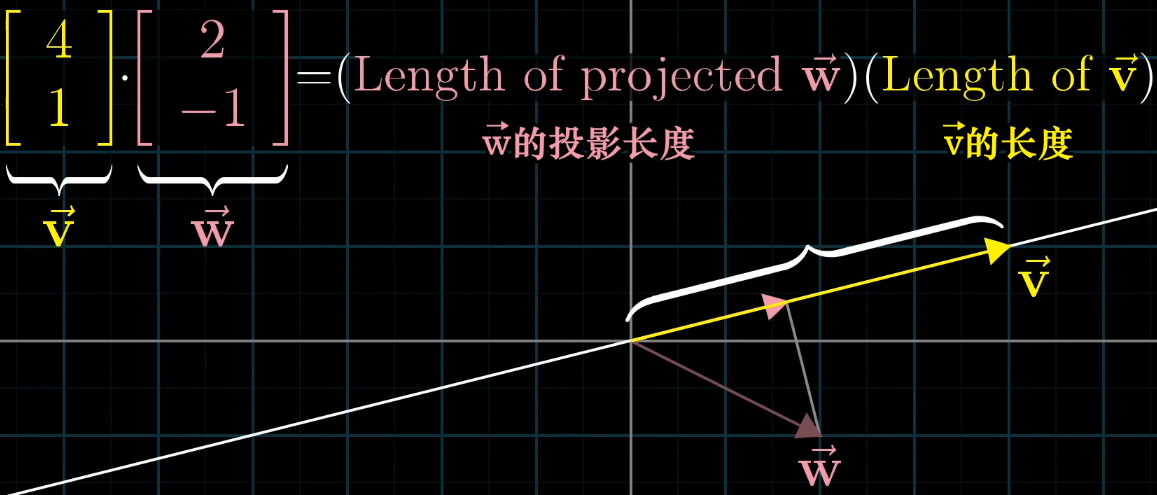
点积的几何意义是 "一个向量在另一个向量上的投影长度与被投影向量长度的乘积"，即：
v ⃗ ⋅ w ⃗ = ∥ v ⃗ ∥ ⋅ ∥ w ⃗ ∥ ⋅ cos ⁡ θ \vec {v} \cdot \vec {w} = \|\vec {v}\| \cdot \|\vec {w}\| \cdot \cos\theta v ⋅w =∥v ∥⋅∥w ∥⋅cosθ

其中 θ \theta θ 是 v ⃗ \vec {v} v 与 w ⃗ \vec {w} w 的夹角， ∥ v ⃗ ∥ = v 1 2 + v 2 2 + ⋯ + v n 2 \|\vec {v}\| = \sqrt {v_1^2 + v_2^2 + \cdots + v_n^2} ∥v ∥=v12+v22+⋯+vn2 是 v ⃗ \vec {v} v 的长度（模）。

符号含义： cos ⁡ θ > 0 \cos\theta > 0 cosθ>0（ θ < 9 0 ∘ \theta < 90^\circ θ<90∘）时，点积为正； cos ⁡ θ < 0 \cos\theta < 0 cosθ<0（ θ > 9 0 ∘ \theta > 90^\circ θ>90∘）时，点积为负； cos ⁡ θ = 0 \cos\theta = 0 cosθ=0（ θ = 9 0 ∘ \theta = 90^\circ θ=90∘）时，点积为 0 0 0（两向量垂直）。

8.2 点积的交换律

点积满足交换律： v ⃗ ⋅ w ⃗ = w ⃗ ⋅ v ⃗ \vec {v} \cdot \vec {w} = \vec {w} \cdot \vec {v} v ⋅w =w ⋅v ，几何解释如下：

若 ∥ v ⃗ ∥ = ∥ w ⃗ ∥ \|\vec {v}\| = \|\vec {w}\| ∥v ∥=∥w ∥，则 v ⃗ \vec {v} v 在 w ⃗ \vec {w} w 上的投影长度等于 w ⃗ \vec {w} w 在 v ⃗ \vec {v} v 上的投影长度，乘积相等；
若 ∥ v ⃗ ∥ ≠ ∥ w ⃗ ∥ \|\vec {v}\| \neq \|\vec {w}\| ∥v ∥=∥w ∥，设 v ⃗ \vec {v} v 的长度为 k ∥ w ⃗ ∥ k\|\vec {w}\| k∥w ∥，则 v ⃗ \vec {v} v 在 w ⃗ \vec {w} w 上的投影长度为 k k k 倍 w ⃗ \vec {w} w 在 v ⃗ \vec {v} v 上的投影长度，乘积仍相等（如 v ⃗ = 2 u ⃗ \vec {v} = 2\vec {u} v =2u ，则 2 u ⃗ ⋅ w ⃗ = 2 ( u ⃗ ⋅ w ⃗ ) = w ⃗ ⋅ 2 u ⃗ 2\vec {u} \cdot \vec {w} = 2 (\vec {u} \cdot \vec {w}) = \vec {w} \cdot 2\vec {u} 2u ⋅w =2(u ⋅w )=w ⋅2u ）。

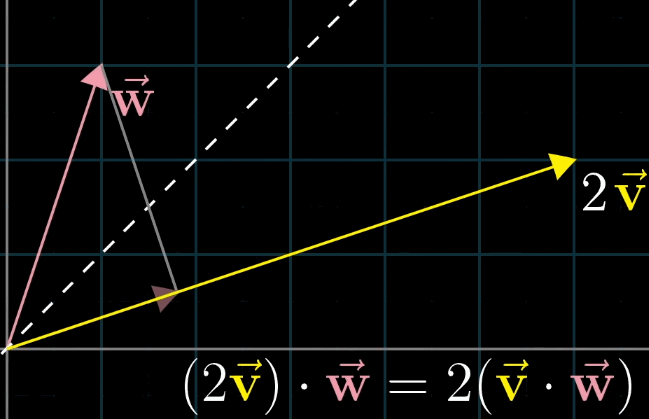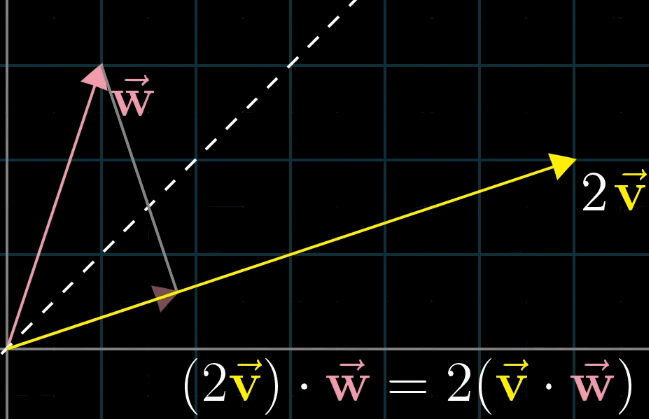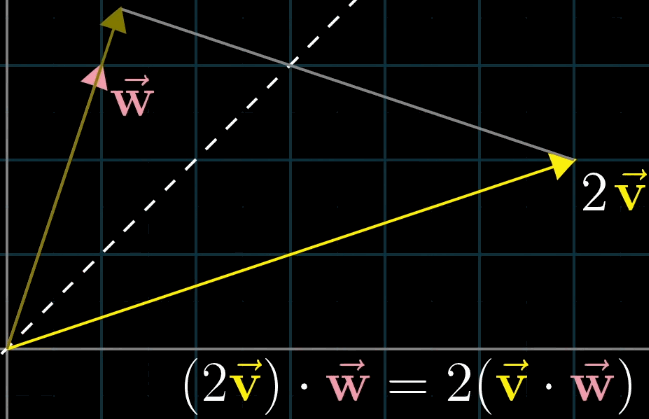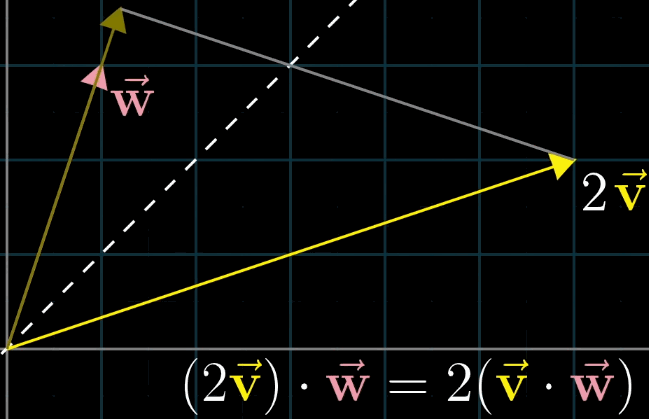
8.3 对偶性：点积与线性变换的对应

8.3.1 多维到一维的线性变换

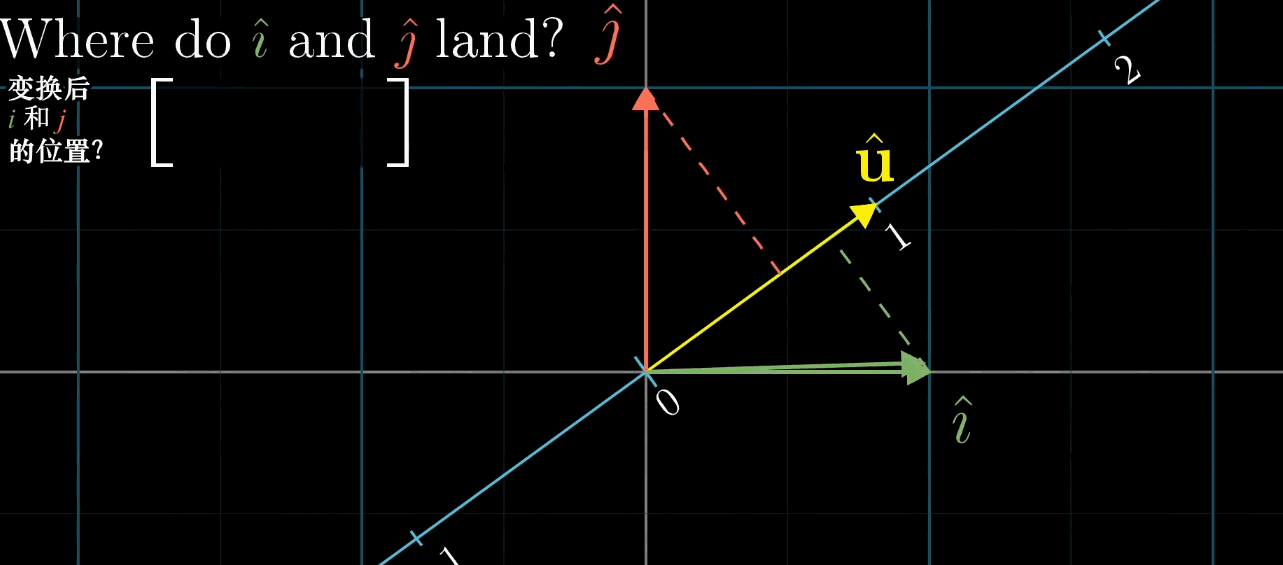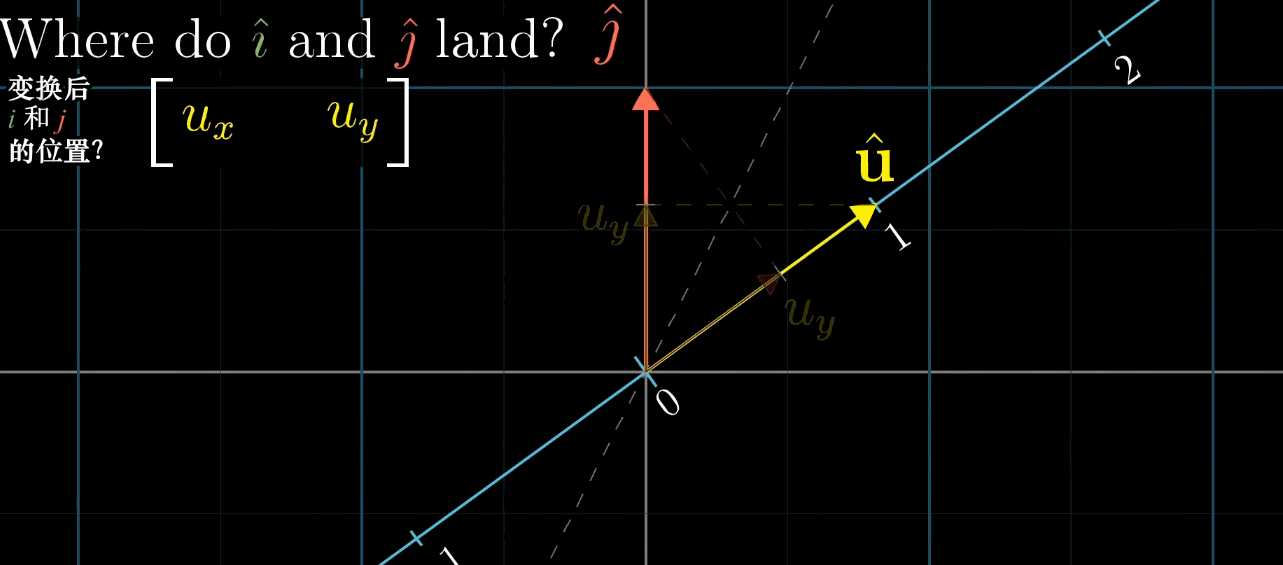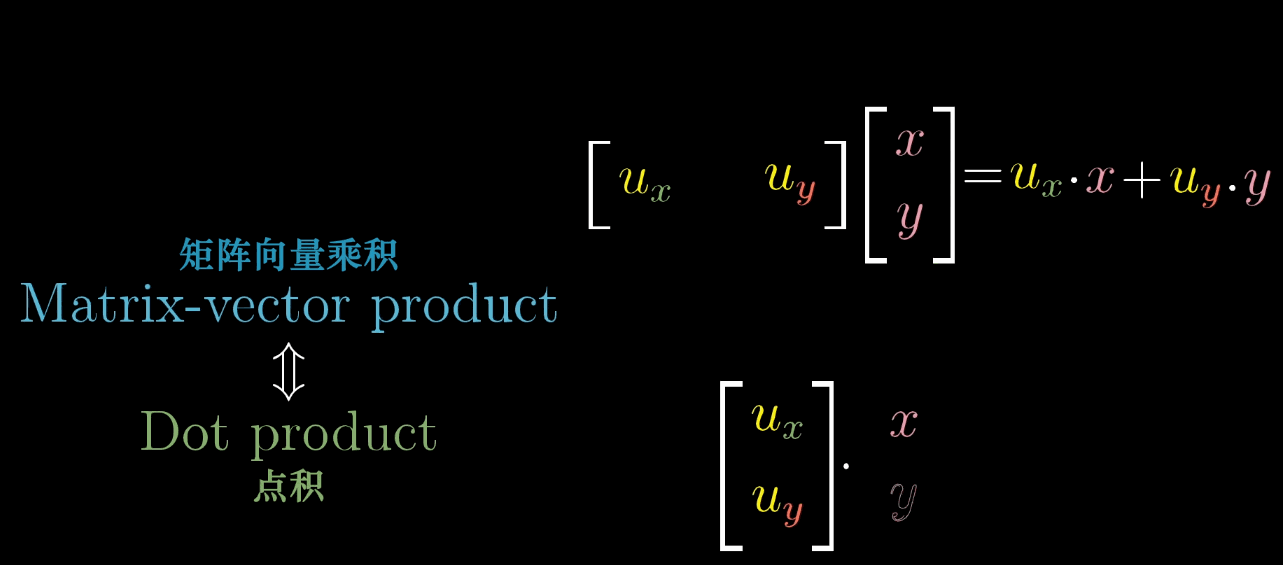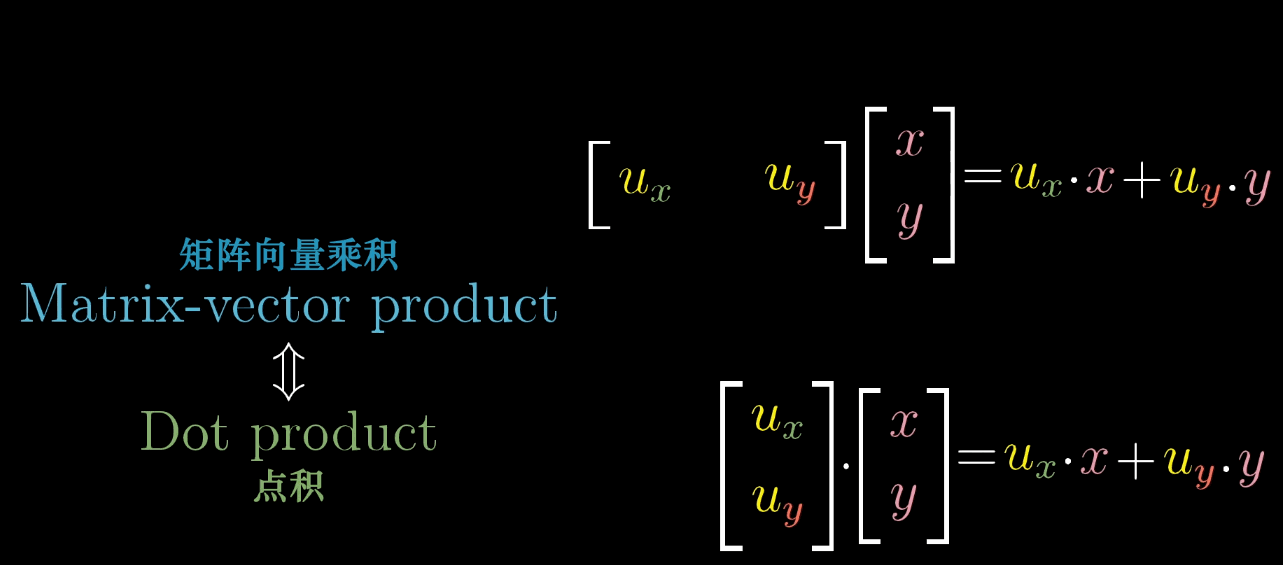
1 × n 1 \times n 1×n 矩阵（行向量）对应的线性变换是将 n n n 维空间映射到一维空间（数轴）。

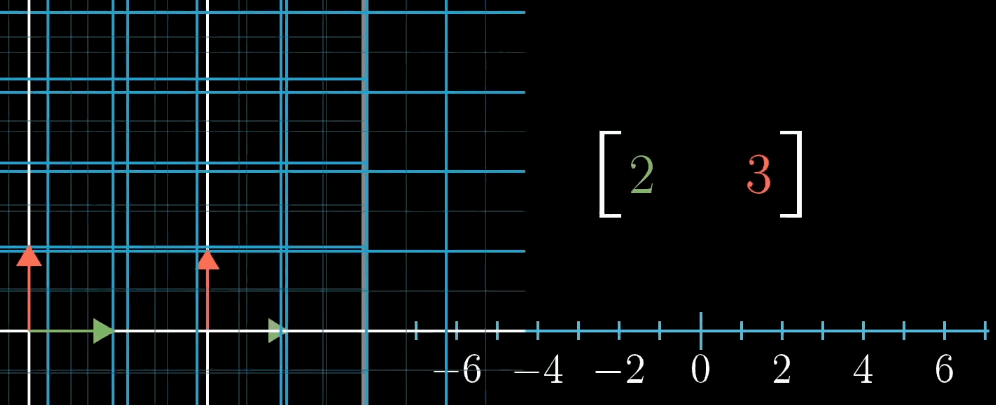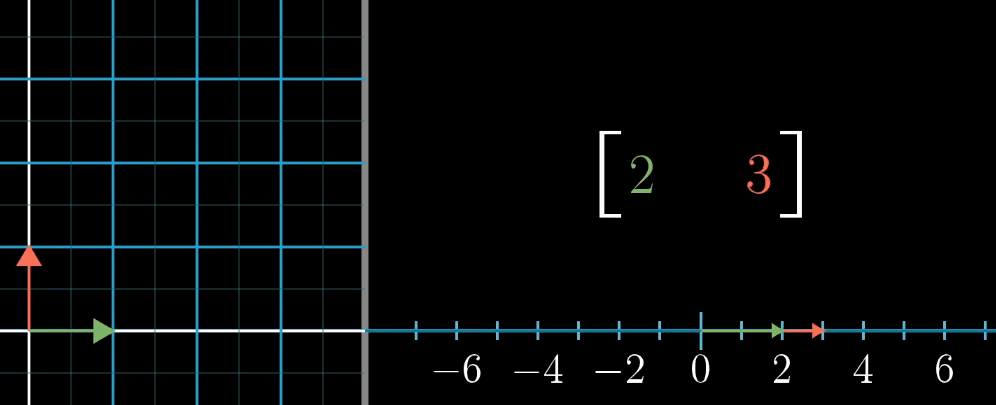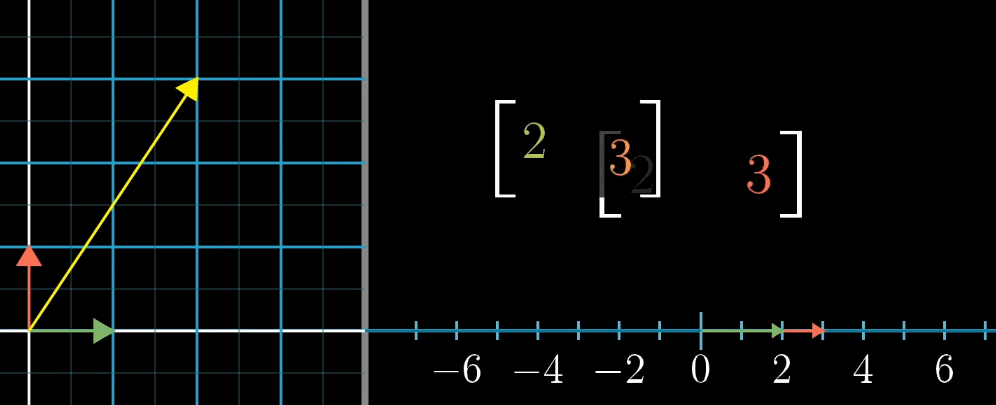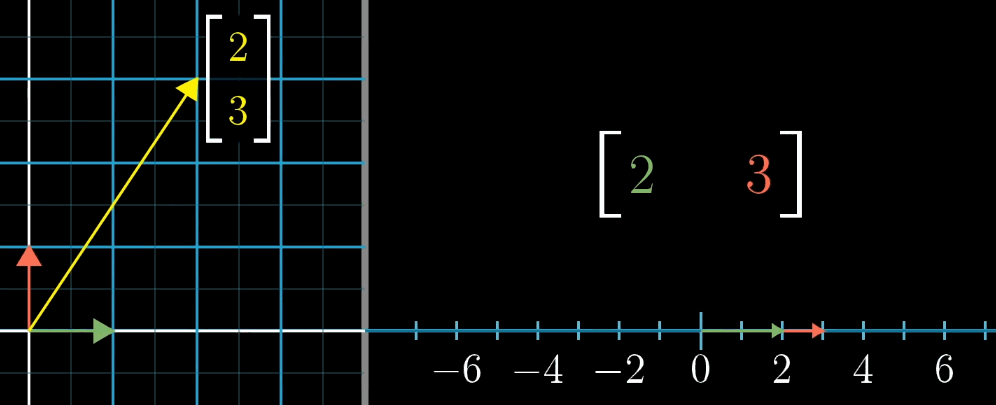
例如， 1 × 2 1 \times 2 1×2 矩阵 [ a b ] \begin {bmatrix} a & b \end {bmatrix} [ab] 对二维向量 [ x y ] \begin {bmatrix} x \\ y \end {bmatrix} [xy] 的变换结果为 a x + b y ax + by ax+by，这与点积 [ a b ] ⋅ [ x y ] \begin {bmatrix} a \\ b \end {bmatrix} \cdot \begin {bmatrix} x \\ y \end {bmatrix} [ab]⋅[xy] 完全一致。

8.3.2 对偶性的定义

对偶性是指 "多维到一维的线性变换" 与 "该空间中的向量" 之间的一一对应关系：

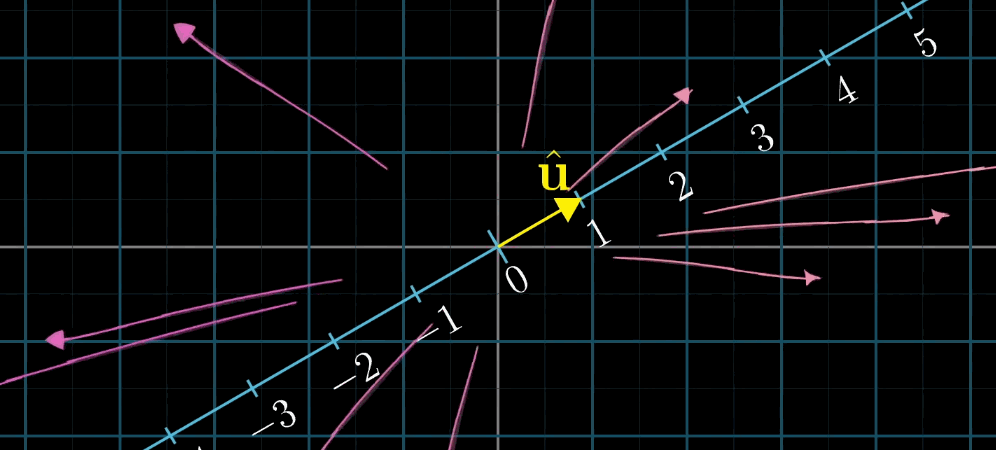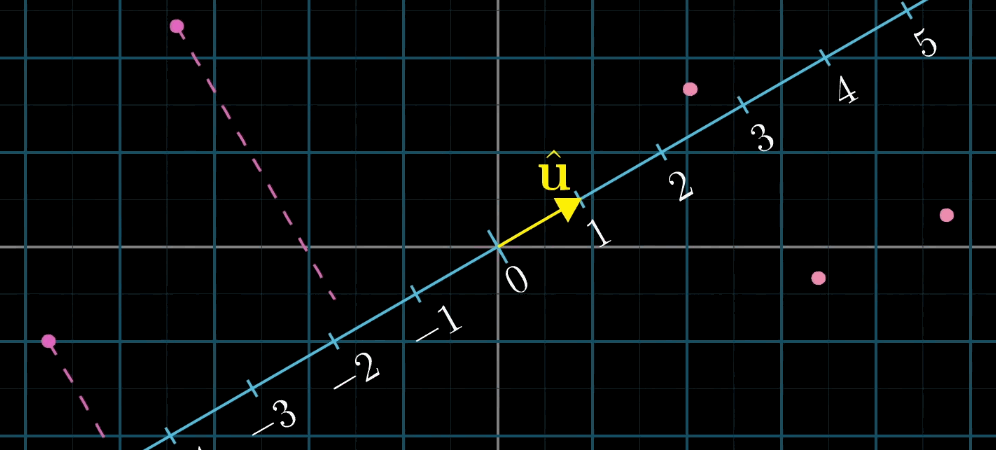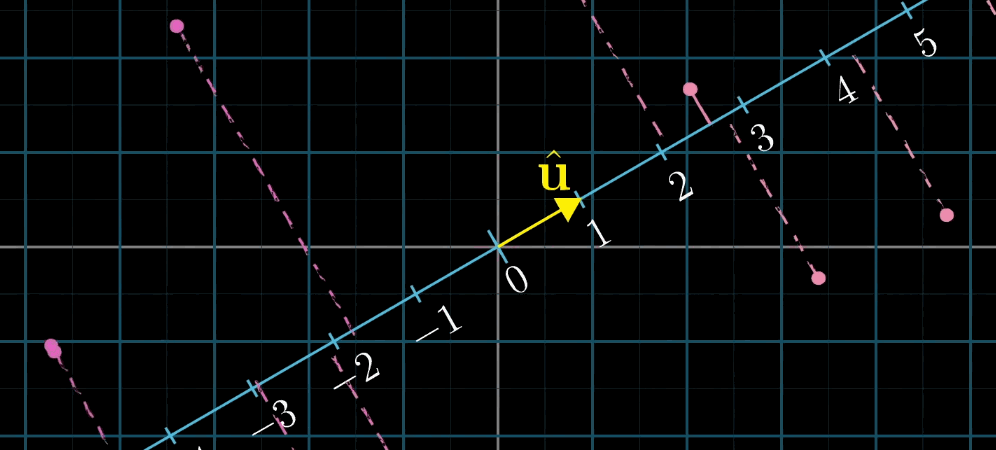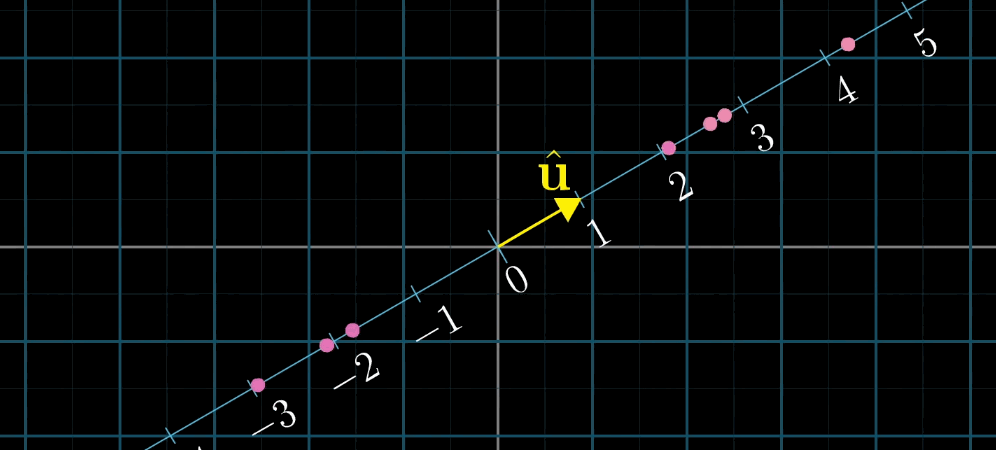
对于任意 n n n 维到一维的线性变换 L ( x ⃗ ) L (\vec {x}) L(x )，存在唯一的 n n n 维向量 u ⃗ \vec {u} u ，使得 L ( x ⃗ ) = u ⃗ ⋅ x ⃗ L (\vec {x}) = \vec {u} \cdot \vec {x} L(x )=u ⋅x ；
反之，任意 n n n 维向量 u ⃗ \vec {u} u 都可定义一个 n n n 维到一维的线性变换 L ( x ⃗ ) = u ⃗ ⋅ x ⃗ L (\vec {x}) = \vec {u} \cdot \vec {x} L(x )=u ⋅x 。

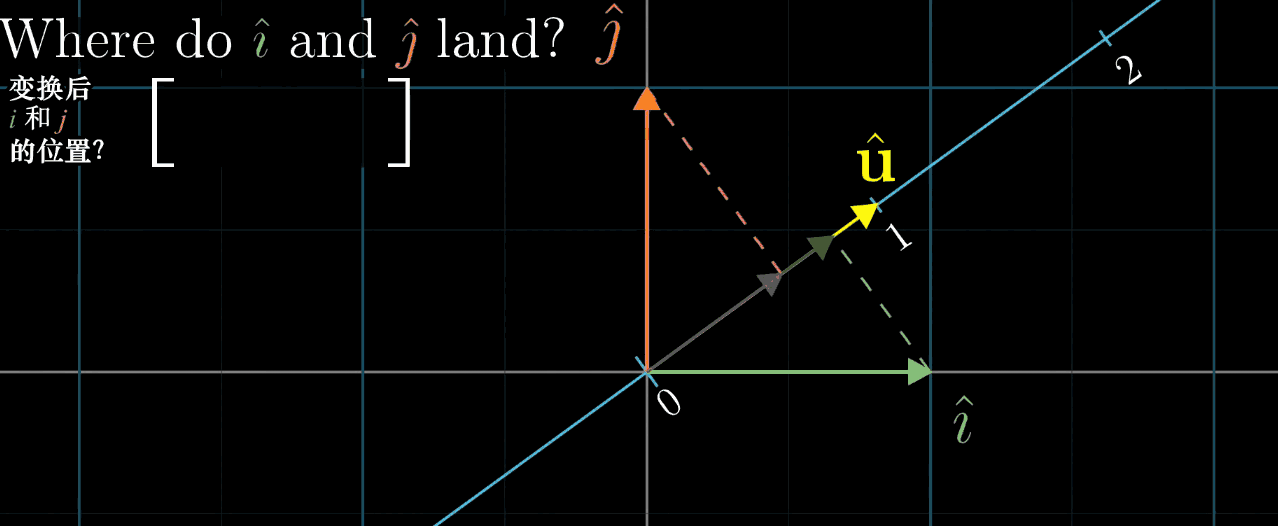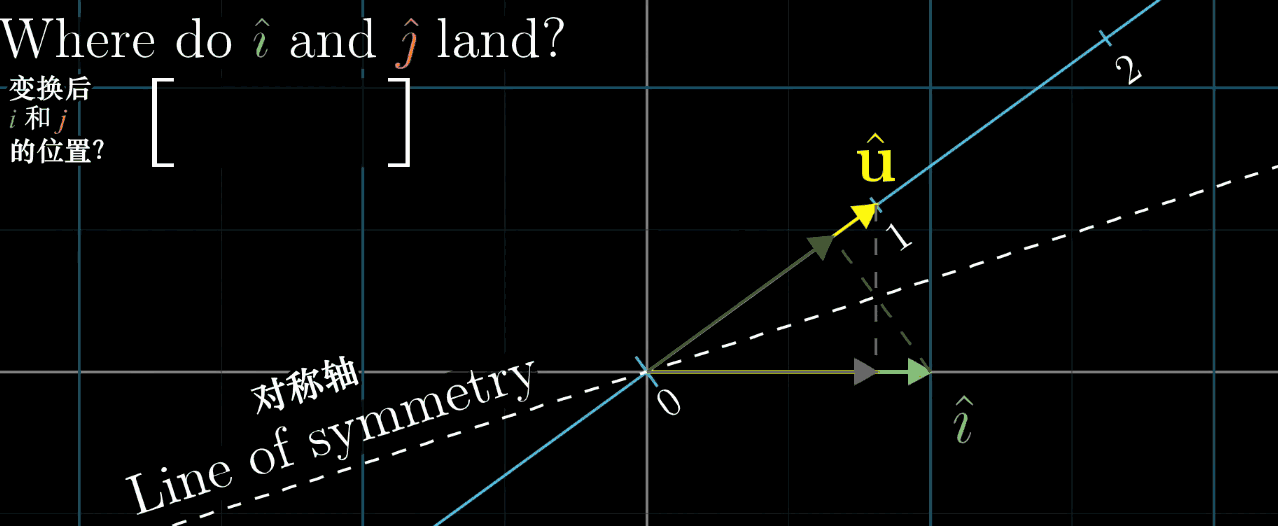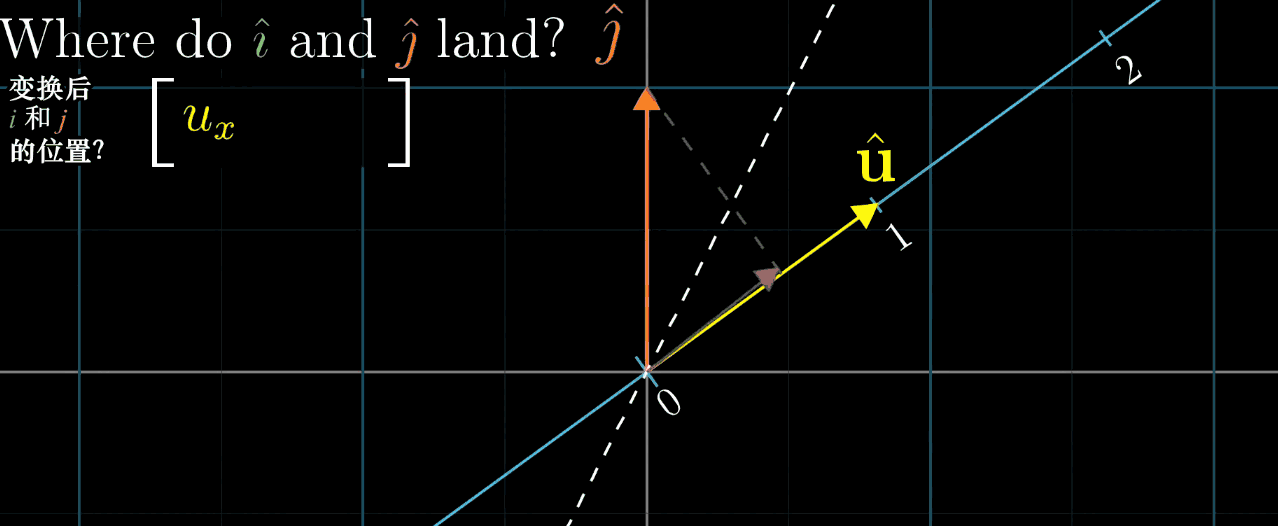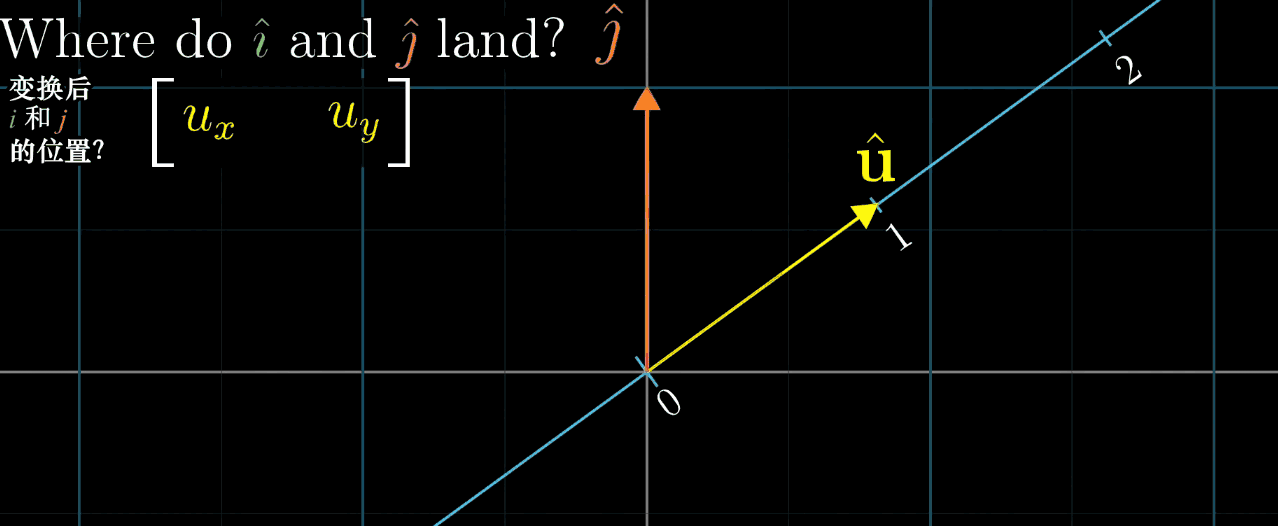
几何解释 ：设 u ⃗ \vec {u} u 是一维空间（数轴）的单位向量， L ( x ⃗ ) L (\vec {x}) L(x ) 是 x ⃗ \vec {x} x 在 u ⃗ \vec {u} u 所在数轴上的投影长度，则 L ( x ⃗ ) = u ⃗ ⋅ x ⃗ L (\vec {x}) = \vec {u} \cdot \vec {x} L(x )=u ⋅x （投影长度等于 x ⃗ \vec {x} x 与单位向量 u ⃗ \vec {u} u 的点积）。

9 叉积

每一个维度都很特别。------ 杰弗里・拉加里亚斯（Jeffrey Lagarias）

从他（格罗滕迪克）和他的作为中，我还学到了一点：不以高难度的证明为傲，因为难度高意味着我们还不理解。理想的情况是能够绘出一幅美景，而其中的证明显而易见。

9.1 二维情况下的叉积类比

在二维空间中，向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形的面积 ，可类比为二维 "叉积"（注：严格意义上的叉积仅定义于三维空间，二维情况实为面积的代数值），记为 v ⃗ × w ⃗ \vec{v} \times \vec{w} v ×w 。

该结果的正负号由基向量 ı ^ \hat{\imath} ^ 和 ȷ ^ \hat{\jmath} ^ 的相对位置关系确定：若 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形中， ȷ ^ \hat{\jmath} ^ 相对于 ı ^ \hat{\imath} ^ 的位置与原始坐标系一致，则结果为正；反之则为负。

结合几何直观，可得出以下结论：

向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 的夹角越接近 9 0 ∘ 90^\circ 90∘（垂直），二者张成的平行四边形面积越大；
叉积满足分配律，即 v ⃗ × ( w ⃗ 1 + w ⃗ 2 ) = v ⃗ × w ⃗ 1 + v ⃗ × w ⃗ 2 \vec{v} \times (\vec{w}_1 + \vec{w}_2) = \vec{v} \times \vec{w}_1 + \vec{v} \times \vec{w}_2 v ×(w 1+w 2)=v ×w 1+v ×w 2。

9.2 真正的叉积定义

严格意义上的叉积 定义于三维空间：给定两个三维向量 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w ，二者的叉积运算将产生一个新的三维向量 p ⃗ \vec{p} p ，且满足以下两个条件：

向量 p ⃗ \vec{p} p 的长度等于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形的面积；
向量 p ⃗ \vec{p} p 的方向与 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w 张成的平面垂直，其具体方向由右手定则 确定：将右手食指指向 v ⃗ \vec{v} v 的方向，中指指向 w ⃗ \vec{w} w 的方向，此时大拇指所指方向即为 p ⃗ \vec{p} p 的方向。

9.3 叉积计算公式

三维向量叉积的计算公式可通过行列式形式表示，如下所示：

v ⃗ × w ⃗ = [ v 1 v 2 v 3 ] × [ w 1 w 2 w 3 ] = det ⁡ ( ı ^ v 1 w 1 ȷ ^ v 2 w 2 k ^ v 3 w 3 ) \vec{v} \times \vec{w} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix} = \det\begin{pmatrix} \hat{\imath} & v_1 & w_1 \\ \hat{\jmath} & v_2 & w_2 \\ \hat{k} & v_3 & w_3 \end{pmatrix} v ×w = v1v2v3 × w1w2w3 =det ^^k^v1v2v3w1w2w3

展开上述行列式，可得：

v ⃗ × w ⃗ = ı ^ ( v 2 w 3 − v 3 w 2 ) − ȷ ^ ( v 1 w 3 − v 3 w 1 ) + k ^ ( v 1 w 2 − v 2 w 1 ) \vec{v} \times \vec{w} = \hat{\imath}(v_2 w_3 - v_3 w_2) - \hat{\jmath}(v_1 w_3 - v_3 w_1) + \hat{k}(v_1 w_2 - v_2 w_1) v ×w =^(v2w3−v3w2)−^(v1w3−v3w1)+k^(v1w2−v2w1)

其中， ı ^ \hat{\imath} ^、 ȷ ^ \hat{\jmath} ^、 k ^ \hat{k} k^ 为三维空间的标准单位基向量，这三个基向量前面的系数（即 v 2 w 3 − v 3 w 2 v_2 w_3 - v_3 w_2 v2w3−v3w2、 − ( v 1 w 3 − v 3 w 1 ) -(v_1 w_3 - v_3 w_1) −(v1w3−v3w1)、 v 1 w 2 − v 2 w 1 v_1 w_2 - v_2 w_1 v1w2−v2w1）分别对应叉积结果向量 p ⃗ \vec{p} p 的 x x x、 y y y、 z z z 坐标值。

初次接触该公式时，多数学习者难以理解其形式由来，甚至部分教学过程仅要求记忆公式而不解释逻辑。但基于 "直观理解" 的核心原则，需进一步探明公式的推导过程。

9.4 叉积计算的几何直观

在推导前，需再次强化对偶性的核心概念：每当遇到一个从 "多维空间到数轴" 的线性变换时，该空间中必然存在唯一一个向量与之对应 ------"将线性变换作用于某个向量" 的结果，与 "该向量和对应向量的点积运算" 结果完全等价。

叉积的运算过程正是对偶性的典型实例：根据向量 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w 定义一个从三维空间到数轴的特定线性变换，找到该变换的对偶向量，这个对偶向量即为 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 的叉积。具体推导步骤如下：

9.4.1 定义线性变换 f ( u ⃗ ) f(\vec{u}) f(u )

已知三维空间中， 3 × 3 3 \times 3 3×3 矩阵的行列式值等于该矩阵三个列向量（或行向量）张成的平行六面体的体积。若将矩阵的第一列替换为自变量向量 u ⃗ = ( x , y , z ) \vec{u} = (x, y, z) u =(x,y,z)，后两列固定为向量 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w ，则可定义函数：

f ( u ⃗ ) = det ⁡ ( u ⃗ v ⃗ w ⃗ ) f(\vec{u}) = \det\begin{pmatrix} \vec{u} & \vec{v} & \vec{w} \end{pmatrix} f(u )=det(u v w )

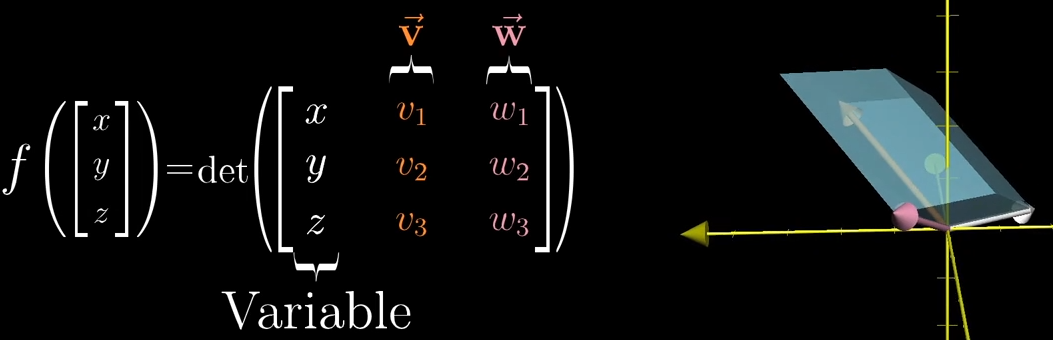
该函数的几何意义为：平行六面体的体积随自变量向量 u ⃗ \vec{u} u 的变化而变化（ "平行六面体随白色向量 ( x , y , z ) (x,y,z) (x,y,z) 的随机游走而不断改变" ）。此时核心问题转化为：根据 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w ，找到一个变换（矩阵或函数），使得上述等式成立。

9.4.2 利用对偶性转化问题

由于 f ( u ⃗ ) f(\vec{u}) f(u ) 满足线性变换的 "可加性" 与 "成比例性"（即线性性质），根据对偶性原理，存在一个三维向量 p ⃗ \vec{p} p ，使得对任意向量 u ⃗ \vec{u} u ，均有：

f ( u ⃗ ) = p ⃗ ⋅ u ⃗ f(\vec{u}) = \vec{p} \cdot \vec{u} f(u )=p ⋅u

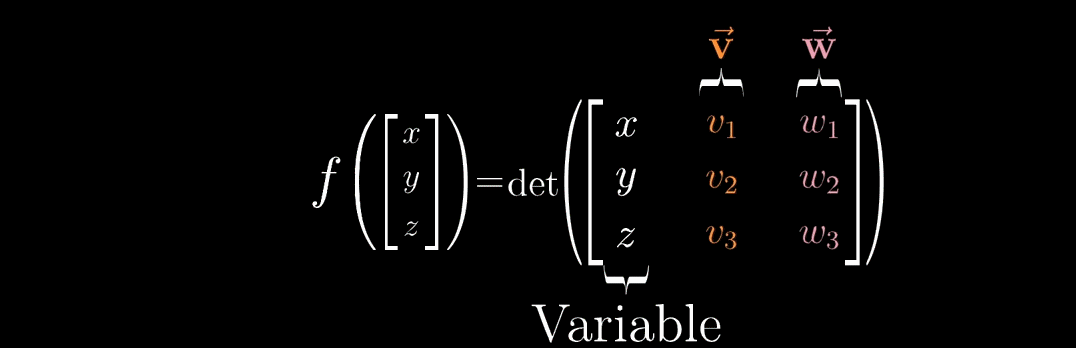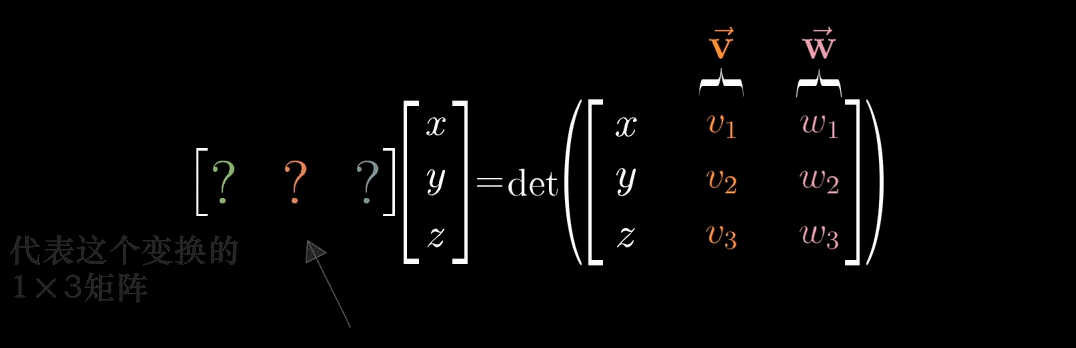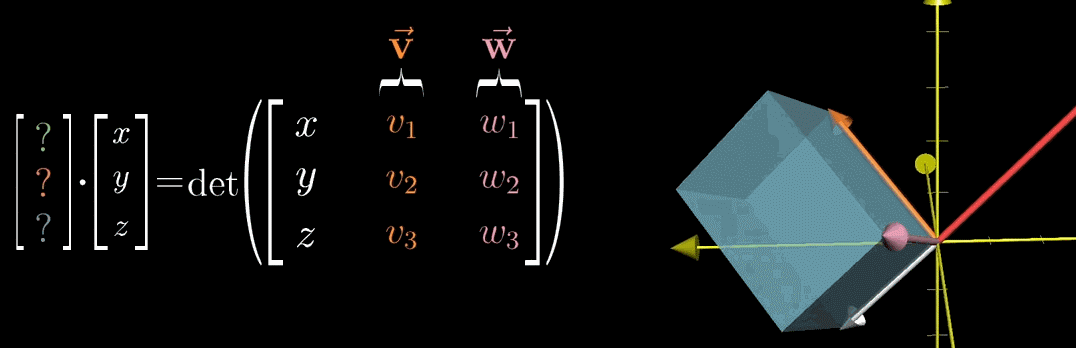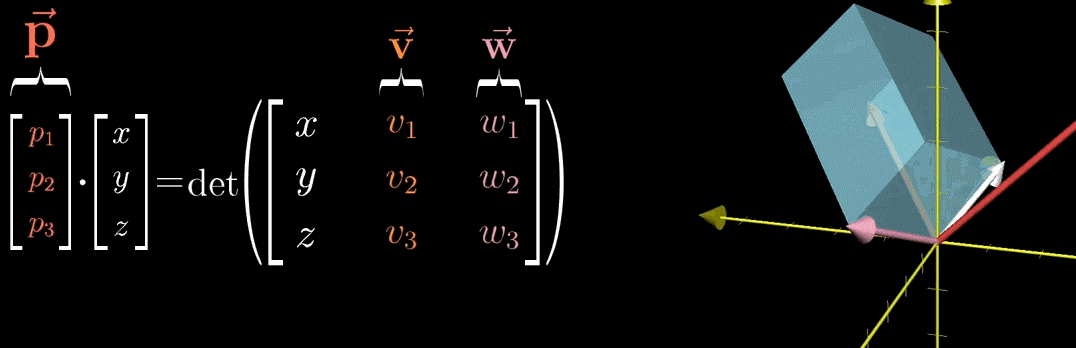
"将 1 × 3 1 \times 3 1×3 的变换矩阵转置，写成点积形式" 的逻辑 ------ 通过对偶性，将 "线性变换作用于 u ⃗ \vec{u} u " 转化为 " u ⃗ \vec{u} u 与 p ⃗ \vec{p} p 的点积"，此时问题进一步转化为：寻找向量 p ⃗ \vec{p} p ，使得上述等式成立。

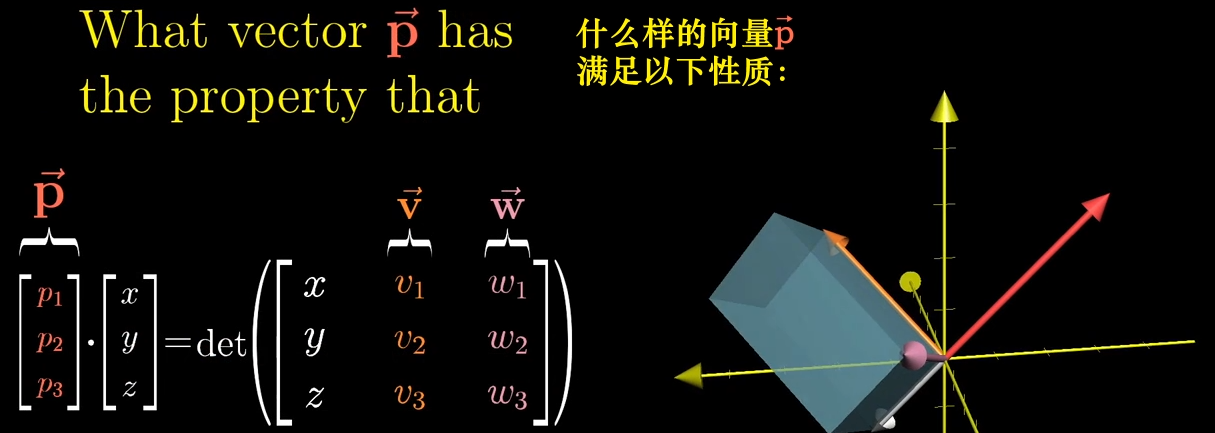
9.4.3 确定 p ⃗ \vec{p} p 的方向与长度

（1） p ⃗ \vec{p} p 的方向：与 v ⃗ \vec{v} v 、 w ⃗ \vec{w} w 张成的平面垂直

根据点积的几何意义， p ⃗ ⋅ u ⃗ \vec{p} \cdot \vec{u} p ⋅u 表示 "将 u ⃗ \vec{u} u 投影到 p ⃗ \vec{p} p 上，投影长度与 p ⃗ \vec{p} p 的长度相乘"；而平行六面体的体积公式为 "底面积 × 高"，其中 "高" 是 u ⃗ \vec{u} u 在 "与底面积垂直方向" 上的投影长度（底面积为 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积）。

为使 "点积结果" 与 "体积" 相等， p ⃗ \vec{p} p 的方向必须与 v ⃗ \vec{v} v 、 w ⃗ \vec{w} w 张成的平面垂直 ------ 只有这样， u ⃗ \vec{u} u 在 p ⃗ \vec{p} p 上的投影长度才等于平行六面体的高，满足 "体积 = 底面积 × 高" 的逻辑。

（2） p ⃗ \vec{p} p 的长度：等于 v ⃗ \vec{v} v 、 w ⃗ \vec{w} w 张成的平行四边形面积

结合点积公式与体积公式：

点积： p ⃗ ⋅ u ⃗ = ∣ p ⃗ ∣ × ∣ u ⃗ 投影 ∣ \vec{p} \cdot \vec{u} = |\vec{p}| \times |\vec{u}{\text{投影}}| p ⋅u =∣p ∣×∣u 投影∣（ ∣ u ⃗ 投影 ∣ |\vec{u}{\text{投影}}| ∣u 投影∣ 为 u ⃗ \vec{u} u 在 p ⃗ \vec{p} p 上的投影长度）；
体积： V = S × ∣ u ⃗ 投影 ∣ V = S \times |\vec{u}_{\text{投影}}| V=S×∣u 投影∣（ S S S 为 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积）。

由于 p ⃗ ⋅ u ⃗ = V \vec{p} \cdot \vec{u} = V p ⋅u =V，代入后可得 ∣ p ⃗ ∣ = S |\vec{p}| = S ∣p ∣=S，即 p ⃗ \vec{p} p 的长度等于 v ⃗ \vec{v} v 与 w ⃗ \vec{w} w 张成的平行四边形面积。

9.4.4 对偶性的价值

通过上述推导，再次验证了对偶性的意义 ------ 它建立了 "线性变换" 与 "向量" 之间自然且出乎意料的对应关系。基于几何直观理解叉积公式的由来，而非单纯记忆，是加深概念记忆、实现深度理解的有效途径。

9.5 总结

通过以下步骤可回顾叉积的核心逻辑，检验对概念的掌握程度：

基于 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w ，定义一个从三维空间到数轴的线性变换 f ( u ⃗ ) = det ⁡ ( u ⃗ v ⃗ w ⃗ ) f(\vec{u}) = \det\begin{pmatrix} \vec{u} & \vec{v} & \vec{w} \end{pmatrix} f(u )=det(u v w )；
利用对偶性，将线性变换 f ( u ⃗ ) f(\vec{u}) f(u ) 转化为 " u ⃗ \vec{u} u 与某向量 p ⃗ \vec{p} p 的点积"，即 f ( u ⃗ ) = p ⃗ ⋅ u ⃗ f(\vec{u}) = \vec{p} \cdot \vec{u} f(u )=p ⋅u ；
为满足 "点积结果 = 平行六面体体积"，推导得出： p ⃗ \vec{p} p 的方向与 v ⃗ \vec{v} v 、 w ⃗ \vec{w} w 张成的平面垂直，长度等于该平面内平行四边形的面积；
将 ı ^ \hat{\imath} ^、 ȷ ^ \hat{\jmath} ^、 k ^ \hat{k} k^ 代入行列式第一列并展开，即可得到叉积的计算公式，而该行列式的结果向量正是对偶向量 p ⃗ \vec{p} p ，即 v ⃗ × w ⃗ = p ⃗ \vec{v} \times \vec{w} = \vec{p} v ×w =p 。

在几何直观上，这个对偶向量 一定与 v ⃗ \vec{v} v 和 w ⃗ \vec{w} w 垂直，并且其长度与这两个向量张成的平行四边形的面积相同。

10 基变换与坐标转换

Mathematics is the art of givinh the same name to different things -Henri Poincare

数学是一门赋予不同事物相同名称的艺术 ------昂利·庞加莱

10.1 基的定义与坐标表示

设 { b 1 ⃗ , b 2 ⃗ , ⋯ , b n ⃗ } \{\vec {b_1}, \vec {b_2}, \cdots, \vec {b_n}\} {b1 ,b2 ,⋯,bn } 是 n n n 维空间的一组基，任意向量 x ⃗ \vec {x} x 可唯一表示为：
x ⃗ = c 1 b 1 ⃗ + c 2 b 2 ⃗ + ⋯ + c n b n ⃗ \vec {x} = c_1\vec {b_1} + c_2\vec {b_2} + \cdots + c_n\vec {b_n} x =c1b1 +c2b2 +⋯+cnbn

其中 [ c 1 c 2 ⋯ c n ] \begin {bmatrix} c_1 \\ c_2 \\ \cdots \\ c_n \end {bmatrix} c1c2⋯cn 称为 x ⃗ \vec {x} x 在基 { b 1 ⃗ , ⋯ , b n ⃗ } \{\vec {b_1}, \cdots, \vec {b_n}\} {b1 ,⋯,bn } 下的坐标。

10.1.2 标准基与非标准基的转换

设标准基为 { ı ^ , ȷ ^ } \{\hat {\imath}, \hat {\jmath}\} {^,^}（二维），非标准基为 { b 1 ⃗ , b 2 ⃗ } \{\vec {b_1}, \vec {b_2}\} {b1 ,b2 }，其中 b 1 ⃗ = [ 2 1 ] \vec {b_1} = \begin {bmatrix} 2 \\ 1 \end {bmatrix} b1 =[21]， b 2 ⃗ = [ − 1 1 ] \vec {b_2} = \begin {bmatrix} -1 \\ 1 \end {bmatrix} b2 =[−11]（用标准基表示）。

基变换矩阵：将非标准基向量作为列构成矩阵 T = [ 2 − 1 1 1 ] T = \begin {bmatrix} 2 & -1 \\ 1 & 1 \end {bmatrix} T=[21−11]，称为 "从非标准基到标准基的转换矩阵"；
坐标转换：若 x ⃗ \vec {x} x 在非标准基下的坐标为 [ c 1 c 2 ] \begin {bmatrix} c_1 \\ c_2 \end {bmatrix} [c1c2]，则其在标准基下的坐标为 [ x 1 x 2 ] = T [ c 1 c 2 ] \begin {bmatrix} x_1 \\ x_2 \end {bmatrix} = T\begin {bmatrix} c_1 \\ c_2 \end {bmatrix} [x1x2]=T[c1c2]；
逆转换：若已知 x ⃗ \vec {x} x 在标准基下的坐标，其在非标准基下的坐标为 [ c 1 c 2 ] = T − 1 [ x 1 x 2 ] \begin {bmatrix} c_1 \\ c_2 \end {bmatrix} = T^{-1}\begin {bmatrix} x_1 \\ x_2 \end {bmatrix} [c1c2]=T−1[x1x2]，其中 T − 1 T^{-1} T−1 是 T T T 的逆矩阵。

10.2 线性变换在不同基下的矩阵

设线性变换 L L L 在标准基下的矩阵为 M M M，在非标准基 { b 1 ⃗ , b 2 ⃗ } \{\vec {b_1}, \vec {b_2}\} {b1 ,b2 } 下的矩阵为 M ′ M' M′，则 M ′ M' M′ 与 M M M 的关系为：
M ′ = T − 1 M T M' = T^{-1} MT M′=T−1MT

其中 T T T 是从非标准基到标准基的转换矩阵。

10.2.2 几何意义

T T T：将非标准基下的坐标转换为标准基下的坐标；
M M M：在标准基下应用线性变换；
T − 1 T^{-1} T−1：将标准基下的变换结果转换回非标准基下的坐标；
整体效果： M ′ M' M′ 描述了同一线性变换在非标准基下的数字表达。

示例：设 L L L 是 "左旋转 9 0 ∘ 90^\circ 90∘" 的变换，标准基下的矩阵 M = [ 0 − 1 1 0 ] M = \begin {bmatrix} 0 & -1 \\ 1 & 0 \end {bmatrix} M=[01−10]，非标准基转换矩阵 T = [ 2 − 1 1 1 ] T = \begin {bmatrix} 2 & -1 \\ 1 & 1 \end {bmatrix} T=[21−11]，则非标准基下的变换矩阵为：
M ′ = T − 1 M T = 1 3 [ 1 1 − 1 2 ] × [ 0 − 1 1 0 ] × [ 2 − 1 1 1 ] = [ 1 3 − 1 3 2 3 − 1 ] M' = T^{-1} MT = \frac {1}{3}\begin {bmatrix} 1 & 1 \\ -1 & 2 \end {bmatrix} \times \begin {bmatrix} 0 & -1 \\ 1 & 0 \end {bmatrix} \times \begin {bmatrix} 2 & -1 \\ 1 & 1 \end {bmatrix} = \begin {bmatrix} \frac {1}{3} & -\frac {1}{3} \\ \frac {2}{3} & -1 \end {bmatrix} M′=T−1MT=31[1−112]×[01−10]×[21−11]=[3132−31−1]

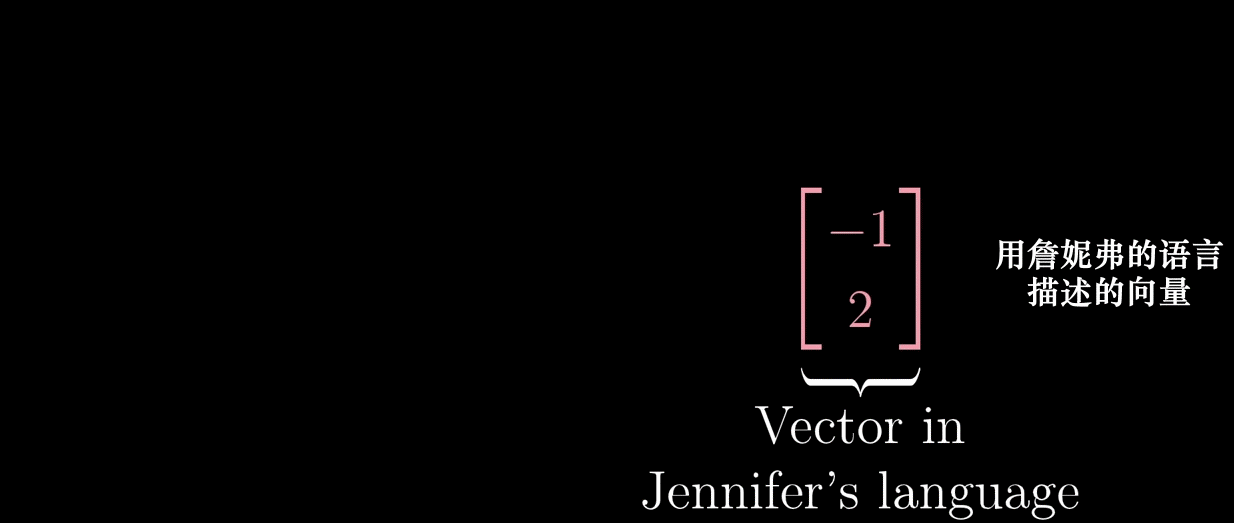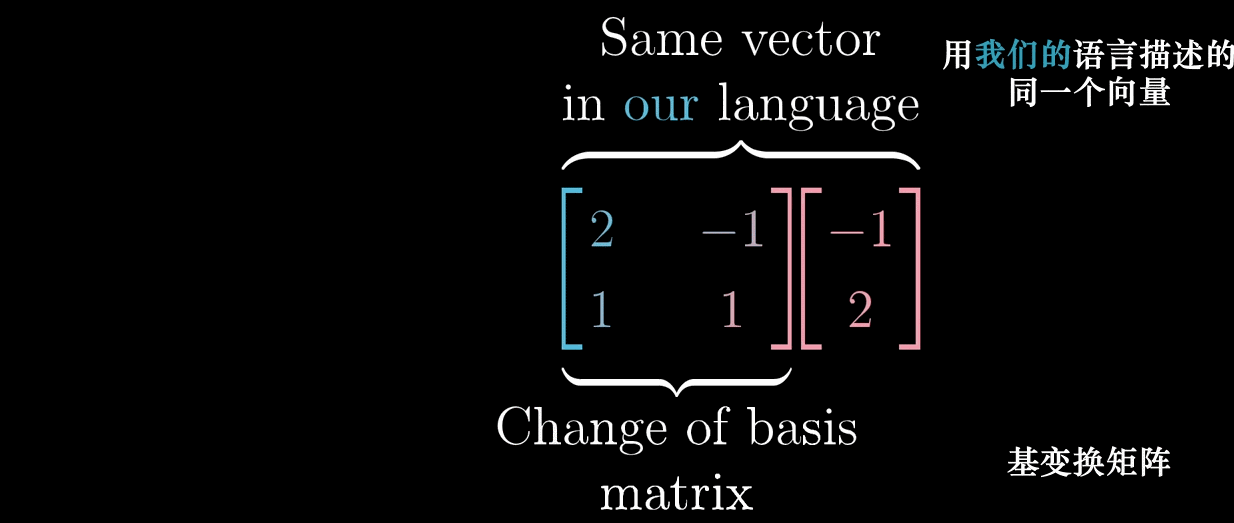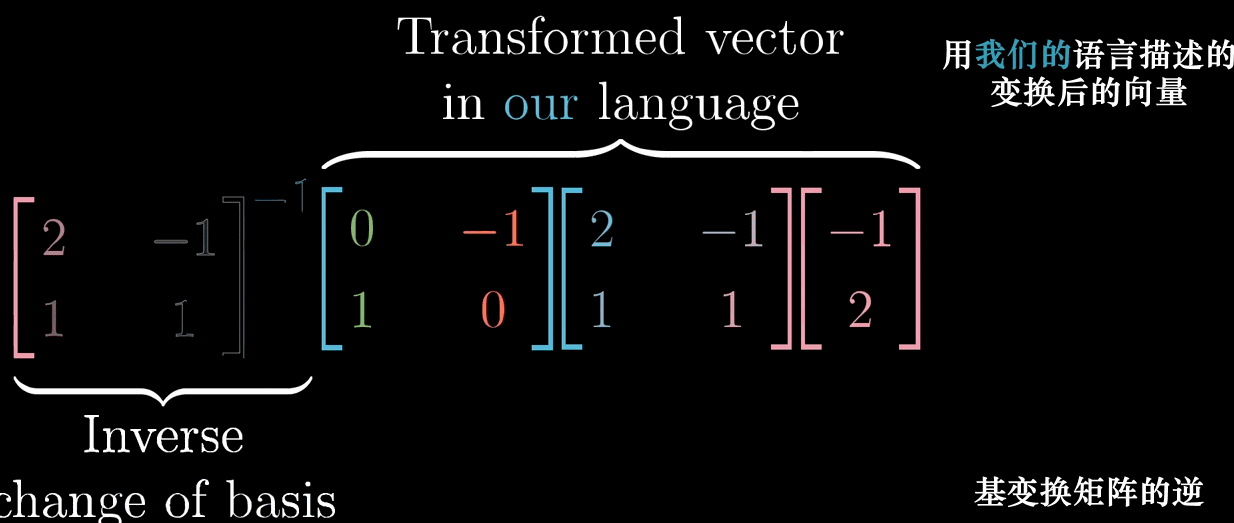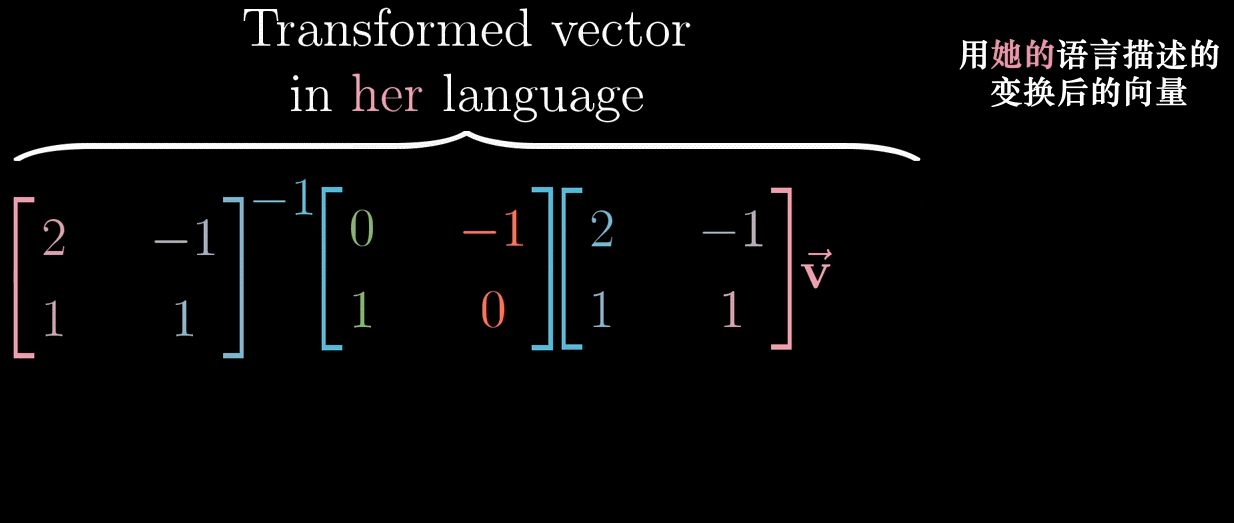
11 特征向量与特征值

本节将系统梳理特征向量与特征值的定义、意义、计算方法及特殊情况，同时探讨特征基的应用，建立其与线性变换、行列式等前置知识的关联，深化对线性代数变换本质的理解。

11.1 特征向量与特征值的定义

设对 ı ^ \hat{\imath} ^ 和 ȷ ^ \hat{\jmath} ^ 张成的空间进行线性变换，基变换为 ı ^ ′ = [ 3 0 ] \hat{\imath}' = \begin{bmatrix} 3 \\ 0 \end{bmatrix} ^′=[30]、 ȷ ^ ′ = [ 1 2 ] \hat{\jmath}' = \begin{bmatrix} 1 \\ 2 \end{bmatrix} ^′=[12]。变换中，大部分向量会脱离自身张成空间（原点到向量终点的直线），但部分向量仍留在该空间内，仅被拉伸或压缩。

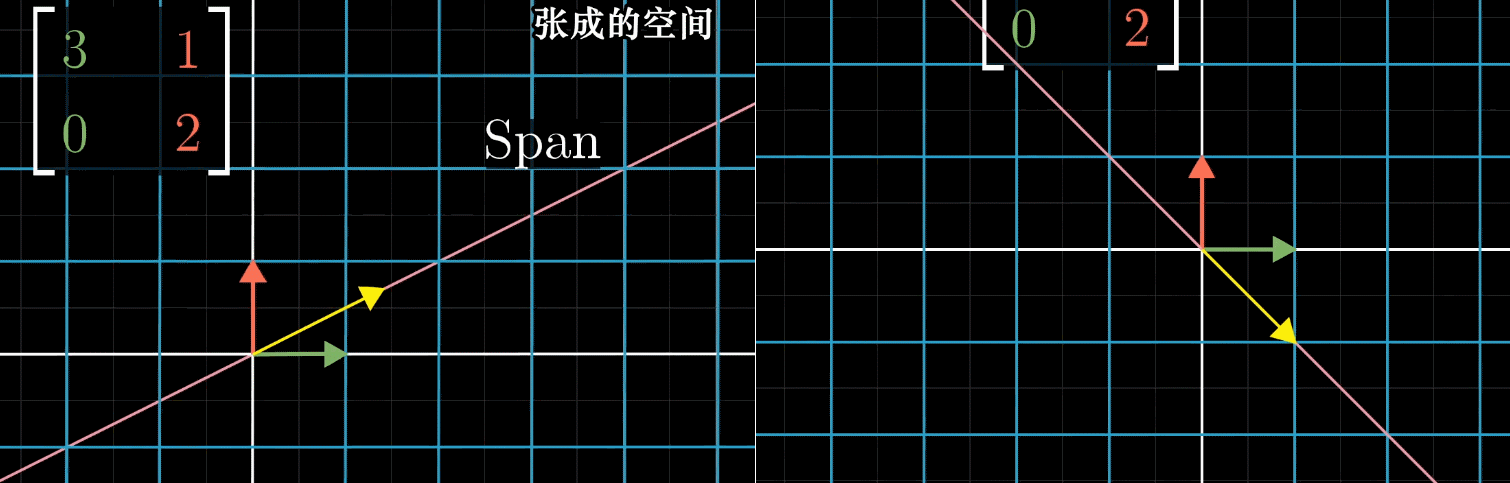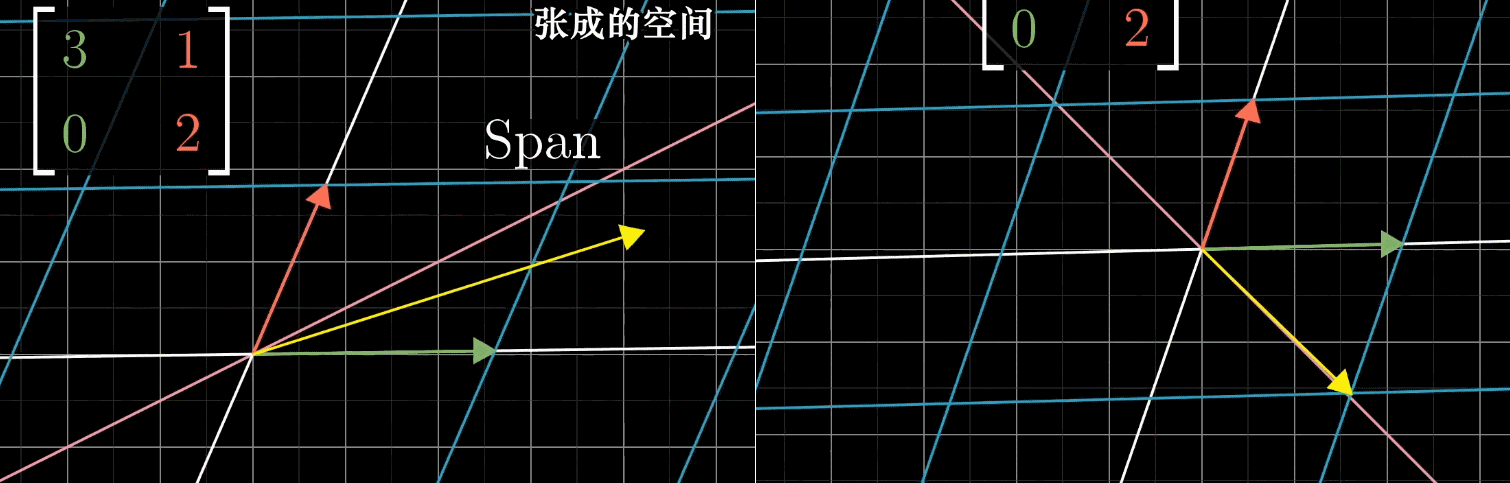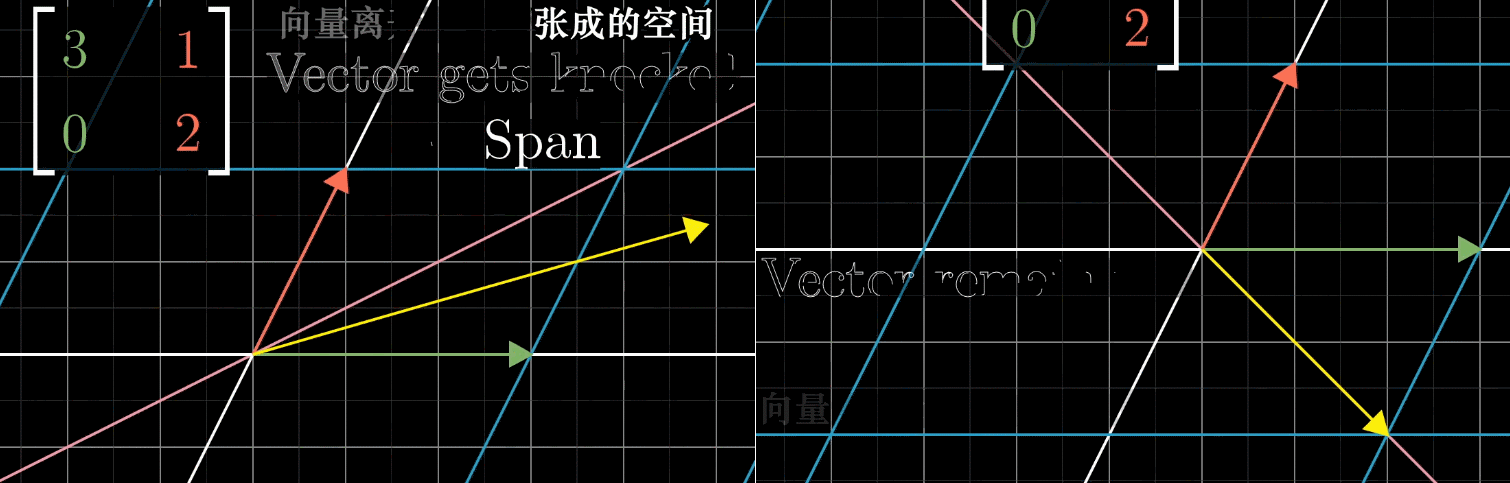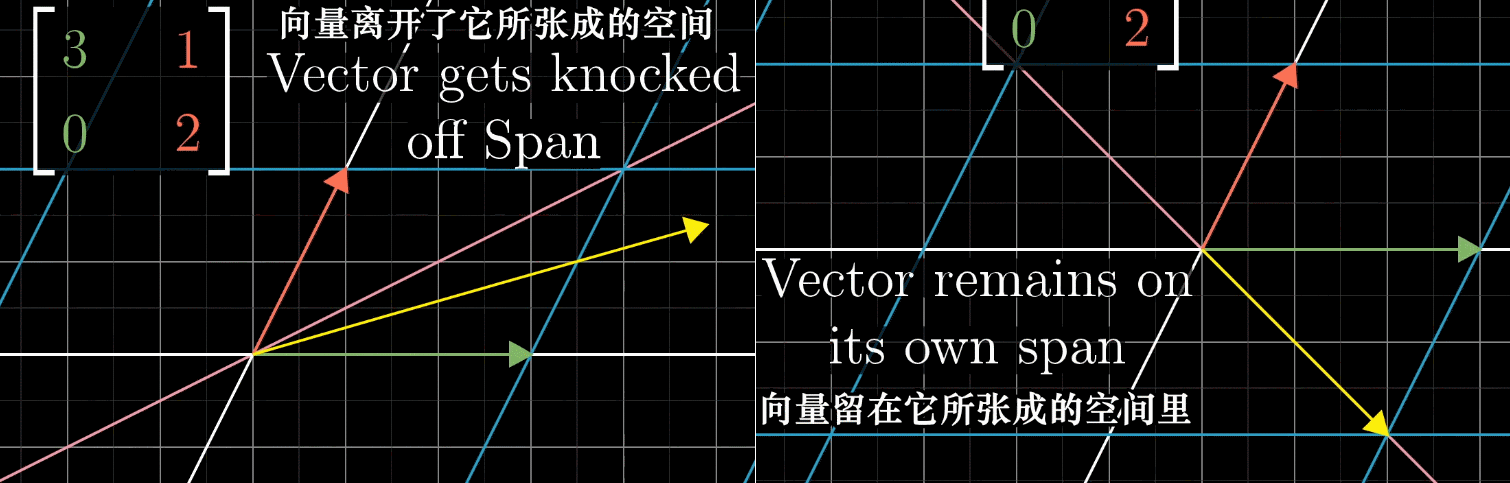
如图所示， x x x 轴上所有向量被伸长为原来的 3 倍，向量 ( − 1 , 1 ) (-1, 1) (−1,1) 被伸长为原来的 2 倍，基于此可给出如下定义：

变换中留在自身张成空间内的向量，称为特征向量 （如 x x x 轴上的向量、 ( − 1 , 1 ) (-1, 1) (−1,1)）；
特征向量被拉伸或压缩的比例因子，称为特征值（如 3、2）；
特征值的正负号，用于表示变换是否使向量发生方向翻转。

11.2 特征向量与特征值的意义

特征向量与特征值是理解线性变换作用的关键工具。以三维空间为例，若能找到旋转轴对应的向量，其特征值必为 1，该向量在旋转变换中保持方向不变，通过这类特征信息可更清晰地描述线性变换的本质。

11.3 特征向量与特征值的计算

根据定义，特征向量与特征值满足数学关系 A v ⃗ = λ v ⃗ A \vec{v} = \lambda \vec{v} Av =λv ，其中 A A A 为变换矩阵， v ⃗ \vec{v} v 为特征向量， λ \lambda λ 为特征值。为便于计算，将等式变形为矩阵乘法形式：

由于 λ v ⃗ \lambda \vec{v} λv 等价于对角矩阵 λ I \lambda I λI 与 v ⃗ \vec{v} v 的乘积（ I I I 为单位矩阵），因此 A v ⃗ = ( λ I ) v ⃗ A \vec{v} = (\lambda I) \vec{v} Av =(λI)v ；
移项可得 ( A − λ I ) v ⃗ = 0 (A - \lambda I) \vec{v} = 0 (A−λI)v =0，该式表示矩阵 A − λ I A - \lambda I A−λI 对 v ⃗ \vec{v} v 的变换会将其压缩到更低维度；
空间压缩对应矩阵行列式为 0，即 det ⁡ ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0，求解该方程可得到特征值 λ \lambda λ，再代入 ( A − λ I ) v ⃗ = 0 (A - \lambda I) \vec{v} = 0 (A−λI)v =0 可求得特征向量 v ⃗ \vec{v} v 。

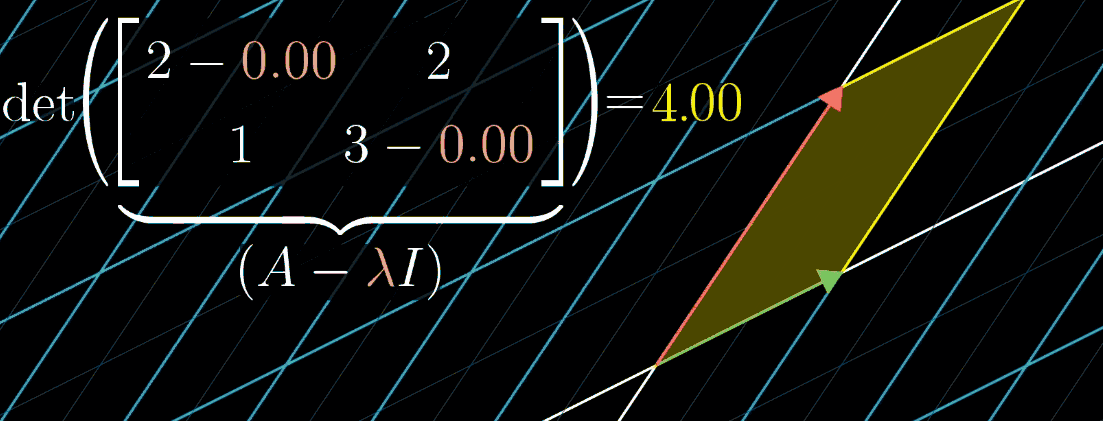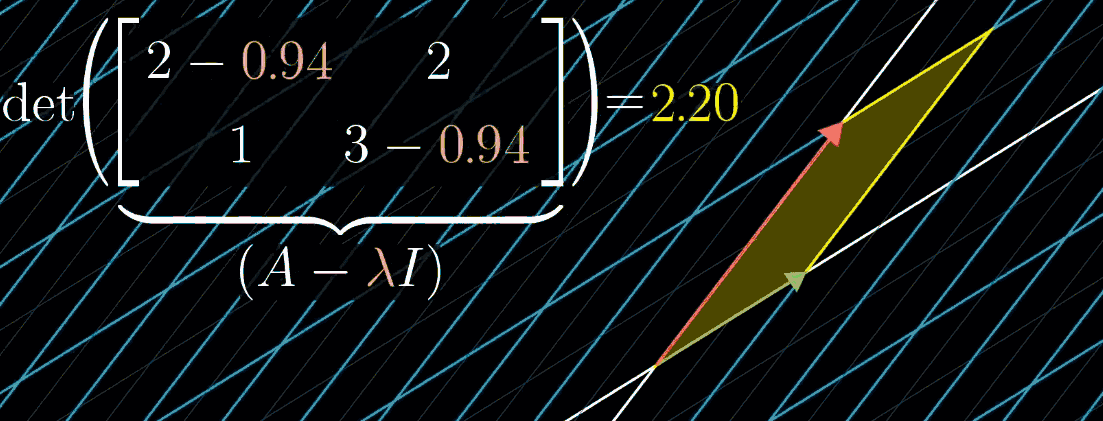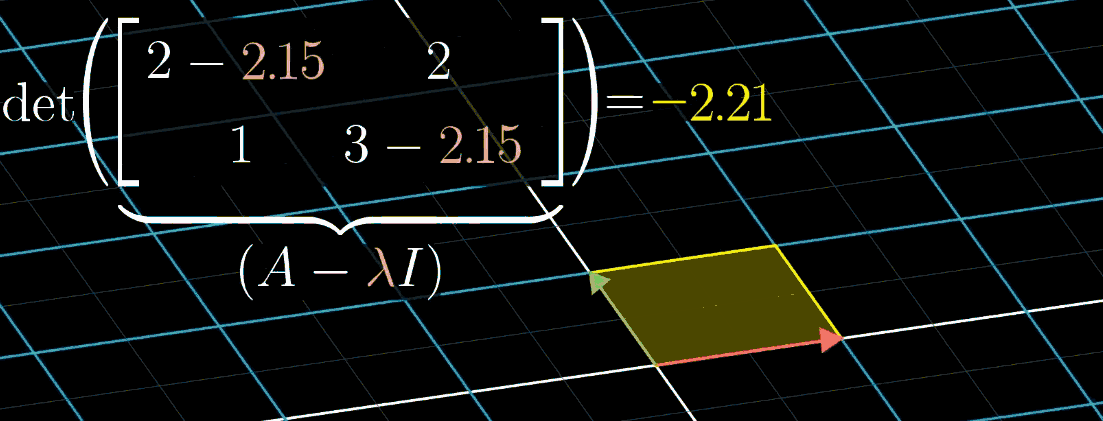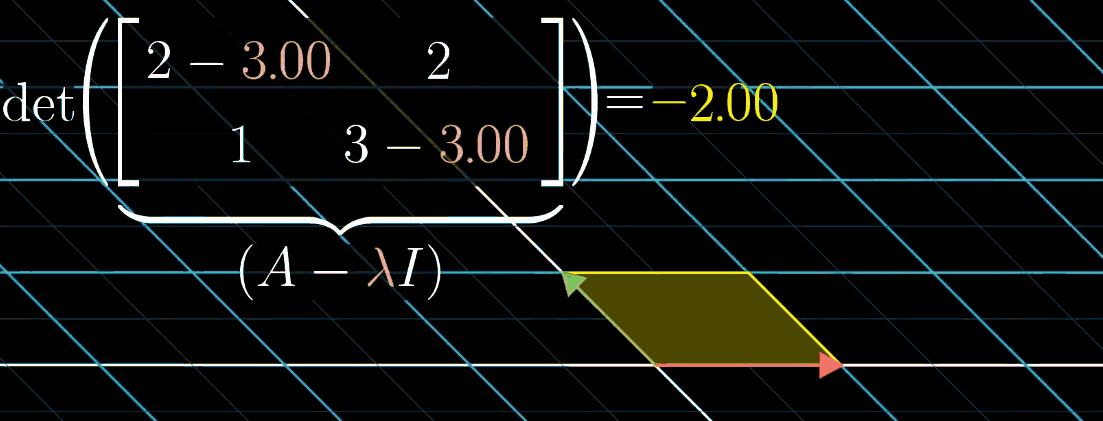
如图所示，随 λ \lambda λ 变化可可视化这一计算过程。例如矩阵 A = [ 2 2 1 3 ] A = \begin{bmatrix} 2 & 2 \\ 1 & 3 \end{bmatrix} A=[2123]，其特征值之一为 1。

11.4 特征向量的特殊情况

11.4.1 旋转变换

对平面旋转变换，求解特征值会得到复数解（如 ± i \pm i ±i），不存在实特征向量。特征值为复数的情况，通常对应变换中的旋转操作。

11.4.2 剪切变换

剪切变换中， x x x 轴保持不变，仅存在一个特征值 λ = 1 \lambda = 1 λ=1（满足 ( λ − 1 ) 2 = 0 (\lambda - 1)^2 = 0 (λ−1)2=0），且特征向量数量不足，无法张成整个空间。

11.4.3 伸缩变换

伸缩变换中，仅有一个特征值，但空间内所有向量均为特征向量，变换仅对所有向量进行统一比例的拉伸或压缩。

11.5 特征基

定义：由特征向量构成的基向量集合，称为特征基。对角矩阵的基向量均为特征向量，因其列向量（对应基向量）仅在自身维度上有非零值，符合特征向量"方向不变"的属性。
优势：对角矩阵的多次乘法计算简便，例如 A n A^n An（ A A A 为对角矩阵）仅需对对角线元素取 n n n 次幂。
应用：若矩阵可对角化，可通过基变换将其转化为对角矩阵计算：以特征向量为基构建变换矩阵 P P P，则 P − 1 A P P^{-1}AP P−1AP 为对角矩阵（对角元素为特征值），计算后再通过 P P P 转换回原空间。

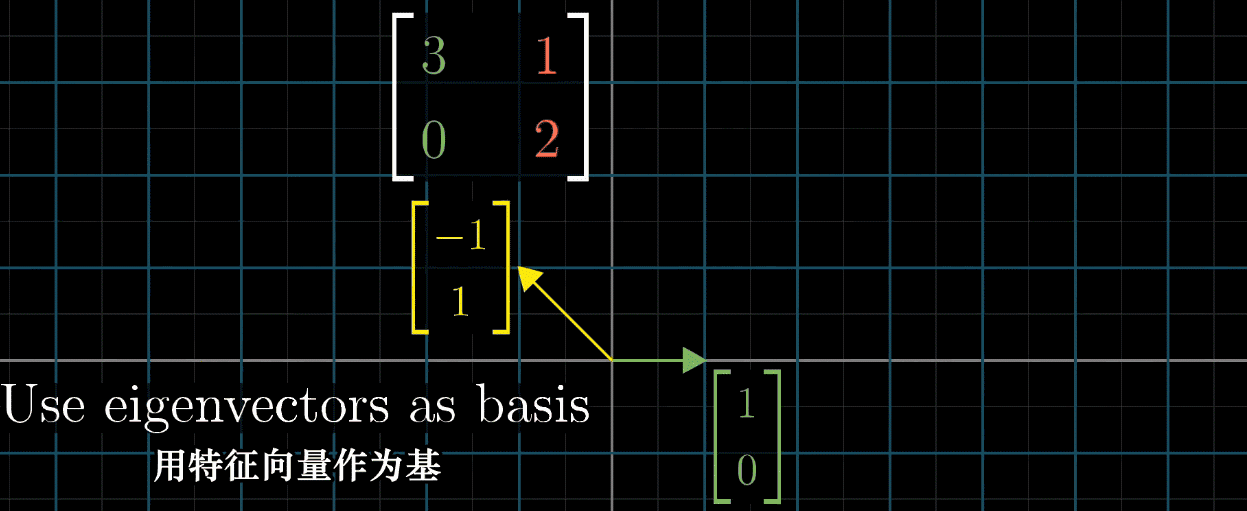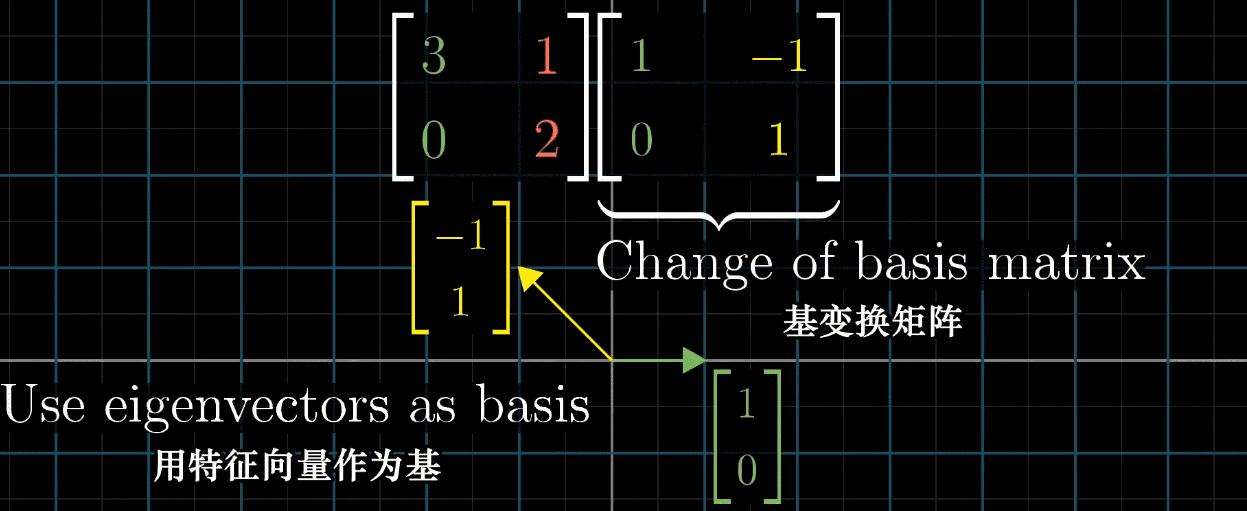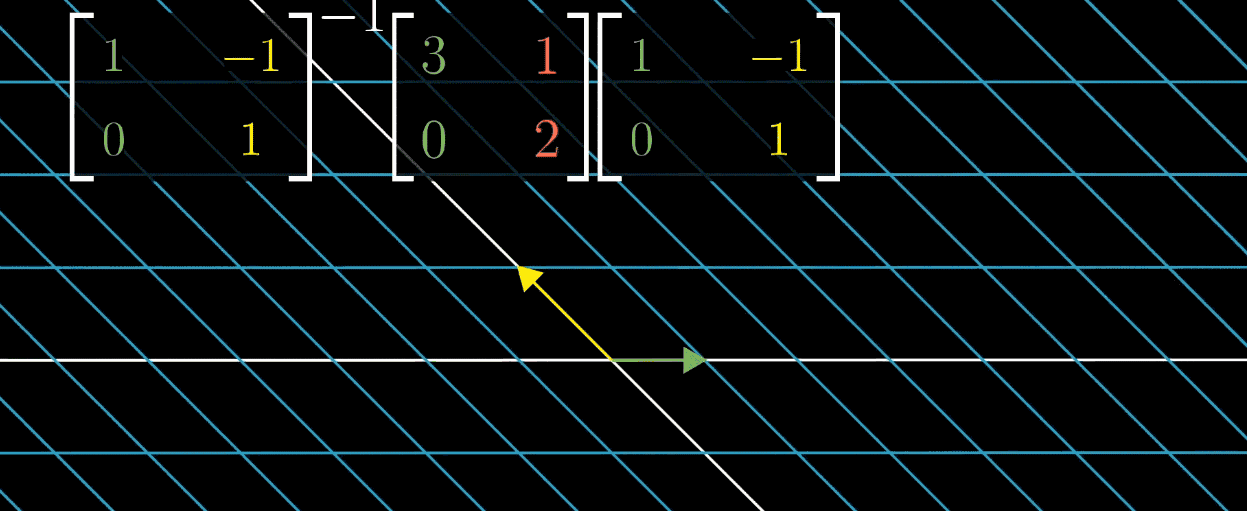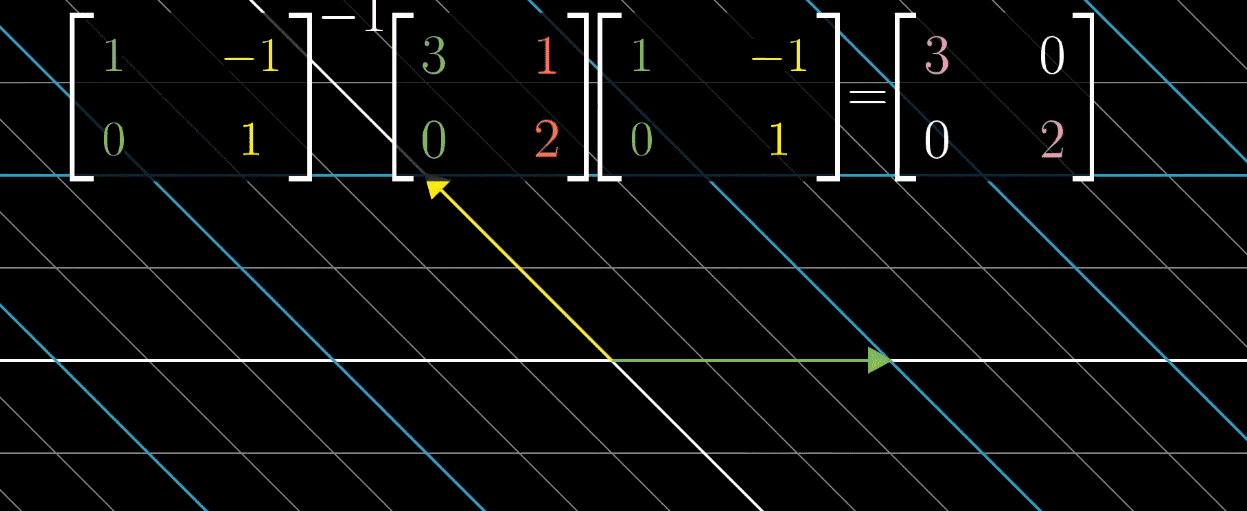
需注意，并非所有矩阵都能对角化，如剪切变换因特征向量数量不足，无法构建特征基。

12 抽象向量空间

线性代数的关键概念（如行列式、特征向量）不受坐标系限制，是空间的固有属性。

本节将线性代数的应用范围从"箭头向量"扩展到更广泛的抽象对象，构建抽象向量空间的理论框架。

12.1 函数与向量的等价性

函数可视为一种特殊的"向量"，因其满足向量的关键运算性质：

可加性： ( f + g ) ( x ) = f ( x ) + g ( x ) (f + g)(x) = f(x) + g(x) (f+g)(x)=f(x)+g(x)，即两个函数在任意点的函数值之和，对应向量加法；
数乘性： ( k f ) ( x ) = k f ( x ) (kf)(x) = kf(x) (kf)(x)=kf(x)（ k k k 为标量），即标量与函数值的乘积，对应向量数乘。

基于此，线性代数中矩阵、线性变换等概念可迁移至函数领域。例如，微积分中的导数是典型的函数线性变换，通常称为"线性算子"，其本质与向量空间中的线性变换一致。

以多项式函数为例，可通过矩阵描述求导变换。选取幂函数 { 1 , x , x 2 , x 3 , ... } \{1, x, x^2, x^3, \dots\} {1,x,x2,x3,...} 作为基函数（对应向量空间的基向量），则求导操作可表示为矩阵形式，进一步验证"矩阵是变换的数字表达"这一关键观点。

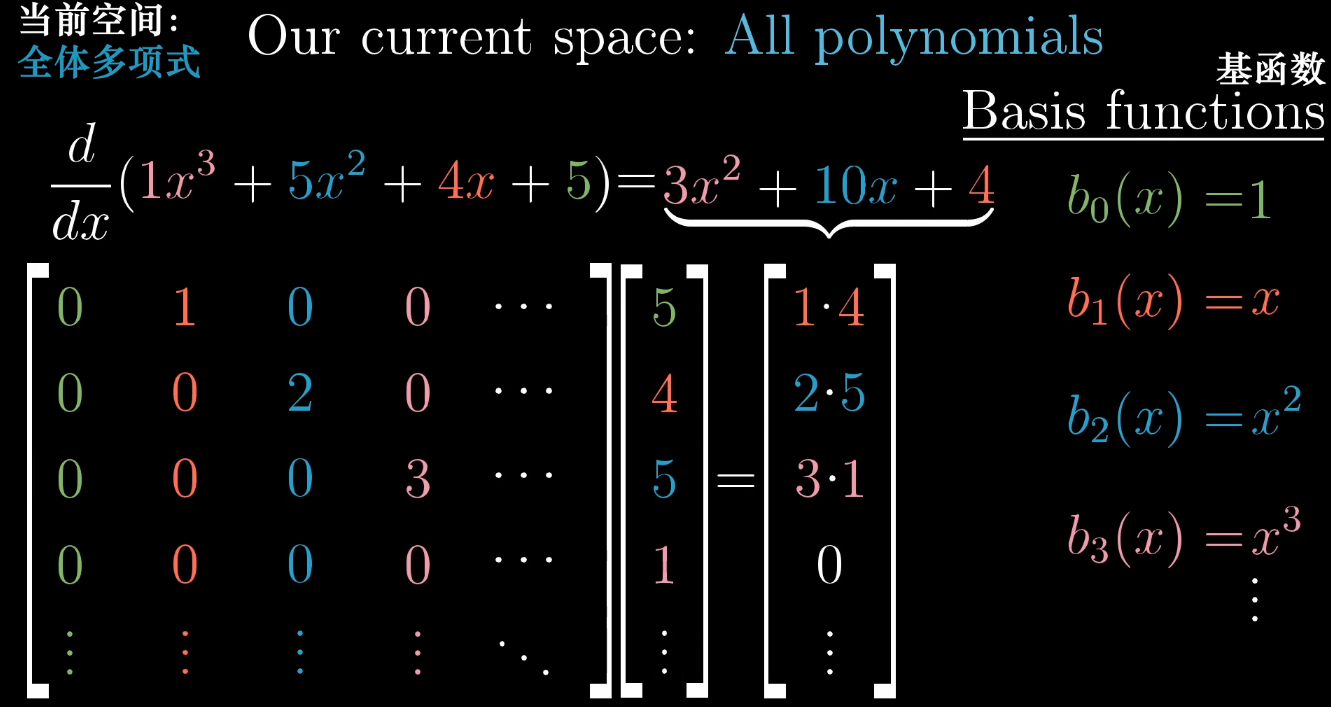
12.2 向量空间的定义与公理

定义：满足向量加法和数乘运算规则的集合，称为向量空间，集合中的元素称为"向量"（如箭头、数组、函数等）。
公理：向量加法与数乘需满足以下 8 条公理，以保证运算的合理性：

向量加法结合律： r ⃗ + ( v ⃗ + w ⃗ ) = ( r ⃗ + v ⃗ ) + w ⃗ \vec{r} + (\vec{v} + \vec{w}) = (\vec{r} + \vec{v}) + \vec{w} r +(v +w )=(r +v )+w ；
向量加法交换律： v ⃗ + w ⃗ = w ⃗ + v ⃗ \vec{v} + \vec{w} = \vec{w} + \vec{v} v +w =w +v ；
加法单位元存在：存在零向量 0 ⃗ \vec{0} 0 ，使得 0 ⃗ + v ⃗ = v ⃗ \vec{0} + \vec{v} = \vec{v} 0 +v =v 对所有 v ⃗ \vec{v} v 成立；
加法逆元存在：对任意向量 v ⃗ \vec{v} v ，存在 − v ⃗ \vec{-v} −v ，使得 v ⃗ + ( − v ⃗ ) = 0 ⃗ \vec{v} + (-\vec{v}) = \vec{0} v +(−v )=0 ；
标量乘法与域乘法相容： a ( b v ⃗ ) = ( a b ) v ⃗ a(b\vec{v}) = (ab)\vec{v} a(bv )=(ab)v （ a , b a, b a,b 为标量）；
标量乘法单位元存在： 1 ⋅ v ⃗ = v ⃗ 1 \cdot \vec{v} = \vec{v} 1⋅v =v ；
标量乘法对向量加法分配律： a ( v ⃗ + w ⃗ ) = a v ⃗ + a w ⃗ a(\vec{v} + \vec{w}) = a\vec{v} + a\vec{w} a(v +w )=av +aw ；
标量乘法对域加法分配律： ( a + b ) v ⃗ = a v ⃗ + b v ⃗ (a + b)\vec{v} = a\vec{v} + b\vec{v} (a+b)v =av +bv 。

这些公理是连接理论与应用的桥梁，确保线性代数结论可推广到各类抽象向量空间。

12.3 函数空间示例：多项式空间

以"所有多项式构成的集合"为例，验证其满足抽象向量空间的定义：

向量加法 ：设多项式 f ( x ) = a n x n + ⋯ + a 1 x + a 0 f(x) = a_nx^n + \dots + a_1x + a_0 f(x)=anxn+⋯+a1x+a0、 g ( x ) = b n x n + ⋯ + b 1 x + b 0 g(x) = b_nx^n + \dots + b_1x + b_0 g(x)=bnxn+⋯+b1x+b0，则 f ( x ) + g ( x ) = ( a n + b n ) x n + ⋯ + ( a 1 + b 1 ) x + ( a 0 + b 0 ) f(x) + g(x) = (a_n + b_n)x^n + \dots + (a_1 + b_1)x + (a_0 + b_0) f(x)+g(x)=(an+bn)xn+⋯+(a1+b1)x+(a0+b0)，符合可加性；
向量数乘 ：对标量 c c c， c ⋅ f ( x ) = c a n x n + ⋯ + c a 1 x + c a 0 c \cdot f(x) = ca_nx^n + \dots + ca_1x + ca_0 c⋅f(x)=canxn+⋯+ca1x+ca0，符合数乘性；
基与维度 ： n n n 次多项式空间的基为 { 1 , x , x 2 , ... , x n } \{1, x, x^2, \dots, x^n\} {1,x,x2,...,xn}，维度为 n + 1 n + 1 n+1（基向量的个数）。

12.4 线性算子：抽象空间的线性变换

在抽象向量空间中，"线性变换"称为线性算子 ，需满足与线性变换相同的条件：对任意向量 u ⃗ , v ⃗ \vec{u}, \vec{v} u ,v 和标量 k k k，有 T ( u ⃗ + v ⃗ ) = T ( u ⃗ ) + T ( v ⃗ ) T(\vec{u} + \vec{v}) = T(\vec{u}) + T(\vec{v}) T(u +v )=T(u )+T(v ) 且 T ( k u ⃗ ) = k T ( u ⃗ ) T(k\vec{u}) = kT(\vec{u}) T(ku )=kT(u )。

12.4.1 导数算子示例

设导数算子 D : D ( f ( x ) ) = f ′ ( x ) D: D(f(x)) = f'(x) D:D(f(x))=f′(x)（作用于多项式空间），验证其线性性：

可加性： D ( f ( x ) + g ( x ) ) = f ′ ( x ) + g ′ ( x ) = D ( f ( x ) ) + D ( g ( x ) ) D(f(x) + g(x)) = f'(x) + g'(x) = D(f(x)) + D(g(x)) D(f(x)+g(x))=f′(x)+g′(x)=D(f(x))+D(g(x))；
数乘性： D ( k f ( x ) ) = k f ′ ( x ) = k D ( f ( x ) ) D(kf(x)) = kf'(x) = kD(f(x)) D(kf(x))=kf′(x)=kD(f(x))。

以 { 1 , x , x 2 } \{1, x, x^2\} {1,x,x2} 为基，多项式 f ( x ) = a + b x + c x 2 f(x) = a + bx + cx^2 f(x)=a+bx+cx2 的坐标为 [ a b c ] \begin{bmatrix} a \\ b \\ c \end{bmatrix} abc ，其导数 f ′ ( x ) = b + 2 c x f'(x) = b + 2cx f′(x)=b+2cx 的坐标为 [ b 2 c 0 ] \begin{bmatrix} b \\ 2c \\ 0 \end{bmatrix} b2c0 ，因此导数算子对应的矩阵为：
D = [ 0 1 0 0 0 2 0 0 0 ] D = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & 0 & 0 \end{bmatrix} D= 000100020

12.5 概念的统一与扩展

抽象向量空间中，线性代数关键概念可对应扩展，不同领域术语本质一致，具体如下表所示：

线性代数术语	抽象向量空间术语	函数空间示例
线性变换	线性算子	导数 D ( f ( x ) ) = f ′ ( x ) D(f(x)) = f'(x) D(f(x))=f′(x)
点积	内积	积分内积 ⟨ f , g ⟩ = ∫ a b f ( x ) g ( x ) d x \langle f, g \rangle = \int_a^b f(x)g(x)dx ⟨f,g⟩=∫abf(x)g(x)dx
特征向量	特征函数	微分方程 D ( f ( x ) ) = λ f ( x ) D(f(x)) = \lambda f(x) D(f(x))=λf(x) 的解 f ( x ) = e λ x f(x) = e^{\lambda x} f(x)=eλx

只要对象满足加法与数乘规则，线性代数的所有结论均可适用，体现了数学规律的普适性。

12.6 总结

向量的本质：向量并非局限于箭头或数组，而是满足加法与数乘公理的抽象对象，类似"3"是对"三个事物"的抽象，向量空间是对"具有线性运算属性的集合"的抽象；
抽象性与普适性 ：抽象性是实现普适性的代价（abstractness is the price of generality）。通过公理定义向量空间，可将线性代数应用于函数、多项式等各类领域；
线性代数的关键框架 ：
1. 向量：满足线性运算的抽象对象；
2. 矩阵：线性变换的数字表达，列向量对应基向量的变换结果；
3. 行列式：空间体积的缩放比例，决定矩阵可逆性；
4. 特征向量/值：变换中方向不变的向量与缩放比例，揭示变换本质；
5. 抽象向量空间：扩展线性代数的应用范围，实现概念统一。

学习线性代数的关键在于建立"几何直观"而非记忆公式，通过理解概念间的关联，可在机器学习、机器人控制等工程领域灵活应用，突破单纯的计算层面。

学习的过程只能来源于解决问题，来源于带有思考的不断重复 ，但如果你具备了正确的直观 ，你会再以后的学习中更加高效。

via:

【直观详解】线性代数的本质 | Go Further | Stay Hungry, Stay Foolish
https://charlesliuyx.github.io/2017/10/06/【直观详解】线性代数的本质/
Determinant - Note201.pdf - 21 February, 2019
https://math.ntnu.edu.tw/~li/Linear/Note201.pdf

线性代数 | 要义 / 本质 （下篇）