生成对抗网络（GAN）

第一部分：生成对抗网络（GAN）简介

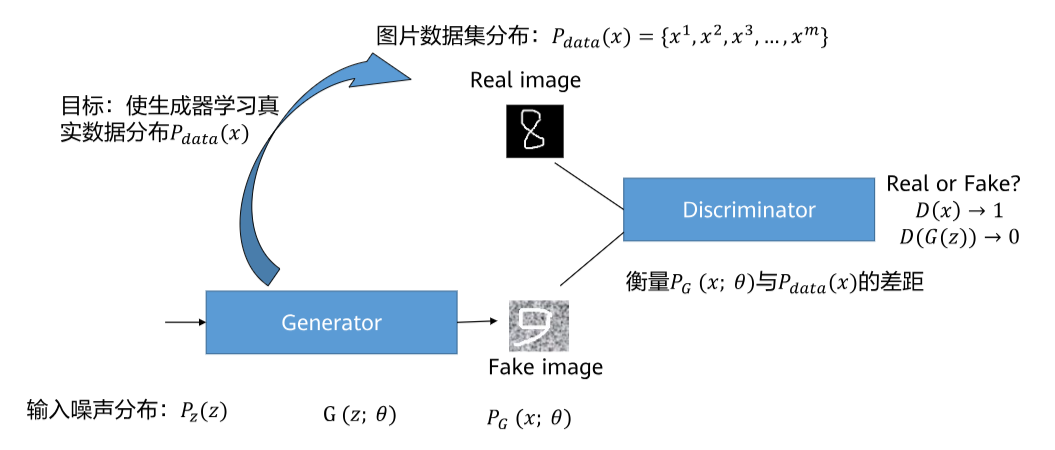
首先，让我们来认识一下生成对抗网络（GAN）。想象一下，GAN就像一场"警察与伪造者"的游戏：

生成器（Generator）：扮演"伪造者"，负责制造假数据（比如假画作），目标是让假数据看起来像真的一样。
判别器（Discriminator）：扮演"警察"，负责区分真数据（比如真实画作）和假数据，目标是尽可能准确地识别真假。

这两个网络相互对抗、共同进步，最终生成器能产生非常逼真的数据。GAN在图像生成、风格迁移等领域应用广泛。

生成对抗网络（Generative Adversarial Network，GAN，英标：/dʒɪˈnɛrətɪv ˌædvərˈsɛəriəl ˈnɛtwɜːrk/）
判别器（Discriminator，D，英标：/dɪˈskrɪmɪneɪtər/）
生成器（Generator，G，英标：/ˈdʒɛnəreɪtər/）
欠拟合（Underfitting，无常用缩写，英标：/ˌʌndərˈfɪtɪŋ/）
过拟合（Overfitting，无常用缩写，英标：/ˌoʊvərˈfɪtɪŋ/）
模式崩塌（Mode Collapse，无常用缩写，英标：/moʊd kəˈlæps/）
不稳定性（Instability，无常用缩写，英标：/ˌɪnstəˈbɪlɪti/）

第二部分：GAN的训练过程

GAN的训练是一个交替优化的过程：先训练判别器（D），再训练生成器（G），反复进行。这就像警察和伪造者轮流学习和改进。

1. 训练判别器（Discriminator）

在训练判别器时，我们固定生成器，只更新判别器的参数。目标是让判别器能准确区分真实数据和生成数据。

原理：判别器接收真实数据（来自训练集）和假数据（来自生成器），并输出一个概率值（0到1之间），表示数据是真实的概率。我们希望判别器对真实数据输出高概率，对假数据输出低概率。
数学公式 ：判别器的损失函数通常定义为：
LD=−Ex∼pdata[log⁡D(x)]−Ez∼pz[log⁡(1−D(G(z)))] L_D = -\mathbb{E}{x \sim p{\text{data}}}[\log D(x)] - \mathbb{E}_{z \sim p_z}[\log(1 - D(G(z)))] LD=−Ex∼pdata[logD(x)]−Ez∼pz[log(1−D(G(z)))]

其中：
- x∼pdatax \sim p_{\text{data}}x∼pdata 表示从真实数据分布中采样的样本。
- z∼pzz \sim p_zz∼pz 表示从噪声分布（如高斯分布）中采样的随机向量。
- G(z)G(z)G(z) 是生成器根据噪声生成的假数据。
- D(x)D(x)D(x) 是判别器对真实数据的输出概率。
- D(G(z))D(G(z))D(G(z)) 是判别器对假数据的输出概率。
- E\mathbb{E}E 表示期望值（平均值）。
  这个损失函数的意义是：判别器要最大化对真实数据的对数概率（log⁡D(x)\log D(x)logD(x)）和最小化对假数据的对数概率（log⁡(1−D(G(z)))\log(1 - D(G(z)))log(1−D(G(z)))）。简单说，就是让判别器"火眼金睛"，正确分类真假。
训练步骤 ：每次迭代中，我们采样一批真实数据和一批假数据，计算损失 LDL_DLD，然后通过梯度下降更新判别器的参数。这就像警察通过观察真画和假画来提升识别能力。

2. 训练生成器（Generator）

在训练生成器时，我们固定判别器，只更新生成器的参数。目标是让生成器产生的假数据能"骗过"判别器，即让判别器对假数据输出高概率。

原理：生成器从噪声中生成数据，我们希望这些数据被判别器误认为是真实的。
数学公式 ：生成器的损失函数可以定义为：
LG=−Ez∼pz[log⁡D(G(z))] L_G = -\mathbb{E}_{z \sim p_z}[\log D(G(z))] LG=−Ez∼pz[logD(G(z))]

这里，生成器要最大化判别器对假数据的输出概率 D(G(z))D(G(z))D(G(z))。换句话说，生成器想让假数据看起来尽可能真实，让判别器"上当"。

有时，这个损失函数也写作 LG=Ez∼pz[log⁡(1−D(G(z)))]L_G = \mathbb{E}_{z \sim p_z}[\log(1 - D(G(z)))]LG=Ez∼pz[log(1−D(G(z)))]，但实践中常用前者来避免梯度消失问题。
训练步骤 ：每次迭代中，我们采样一批噪声，生成假数据，计算损失 LGL_GLG，然后通过梯度下降更新生成器的参数。这就像伪造者根据警察的反馈改进造假技术。

总结训练过程：GAN的训练是交替进行的------先训练判别器几步，再训练生成器几步，反复循环。理想情况下，两者会达到一个平衡点，生成器能产生逼真的数据。但这个过程并不总是顺利的，接下来我们就看看常见问题。

第三部分：GAN训练中存在的问题

GAN训练虽然强大，但像任何复杂系统一样，容易出问题。主要问题包括欠拟合与过拟合、模式崩塌和不稳定性。我会用比喻帮你理解这些问题。

1. 欠拟合（Underfitting）和过拟合（Overfitting）

这两个问题在机器学习中很常见，但在GAN中尤其棘手，因为它们会影响生成器和判别器的平衡。

欠拟合 ：模型太简单，无法捕捉数据的复杂模式。在GAN中，如果生成器或判别器网络太浅或参数太少，就可能欠拟合。
- 例子：想象一个画家（生成器）只会画简单的圆圈，但真实画作是复杂的风景画。无论怎么训练，他都画不出细节，因为能力不足。
- 在GAN中的表现：生成的数据过于简单、模糊，判别器也无法有效区分真假。
过拟合 ：模型太复杂，过度记忆训练数据，导致泛化能力差。在GAN中，判别器容易过拟合。
- 例子：警察（判别器）只记住了训练集中的具体画作，一旦看到稍微不同的假画，就误判为真。这就像背答案而不是理解原理。
- 在GAN中的表现：判别器在训练集上表现完美，但对新生成的假数据识别能力差，导致生成器训练停滞。

2. 模式崩塌（Mode Collapse）

这是GAN特有的问题，指生成器只生成少数几种样本，缺乏多样性。

原理：生成器发现判别器对某些模式（如特定颜色或形状）识别能力弱，就只生成这些模式来"作弊"，而不是学习整个数据分布。
例子：假设真实数据是各种动物图片（猫、狗、鸟），但生成器只生成猫的图片，因为判别器对猫的识别最差。结果，生成器变成了"专画猫的艺术家"，忽略了其他动物。
表现：生成的数据重复、单调，无法覆盖真实数据的所有变化。

3. 不稳定性（Instability）

GAN训练过程常常不稳定，表现为损失函数剧烈振荡、难以收敛，甚至发散。

原理：生成器和判别器的对抗性导致动态平衡问题。如果一方太强，另一方就难以进步，就像"军备竞赛"失控。
例子：警察（判别器）太强大，总能识别假画，伪造者（生成器）就放弃改进；或者伪造者太厉害，警察总是被骗。结果训练过程像坐过山车，无法稳定。
表现：损失值忽高忽低，生成质量时好时坏，有时甚至完全失败。

第四部分：解决和缓解方法

针对以上问题，研究者提出了许多方法。

1. 针对欠拟合和过拟合的方法

调整网络架构 ：使用更深的网络或更多参数来防止欠拟合；添加正则化（如Dropout或权重衰减）来防止过拟合。
- 例子：在判别器中加入Dropout层，随机忽略一些神经元，避免它过度依赖特定特征。
- 数学上 ，权重衰减在损失函数中添加正则项，例如 LD+λ∥θ∥2L_D + \lambda \|\theta\|^2LD+λ∥θ∥2，其中 θ\thetaθ 是参数，λ\lambdaλ 是超参数。
早停（Early Stopping）：监控验证集性能，在过拟合前停止训练。
数据增强：对训练数据进行旋转、缩放等变换，增加多样性，减少过拟合风险。

2. 针对模式崩塌的方法

迷你批判别（Minibatch Discrimination） ：让判别器在批次级别比较样本，而不是单个样本，从而鼓励生成器产生多样化的输出。
- 原理：判别器计算批次内样本的相似度，如果生成器只产生相似样本，判别器就容易识别。
Wasserstein GAN (WGAN) ：使用Wasserstein距离代替原始GAN的JS散度，能更好地衡量分布差异，减少模式崩塌。
- 数学公式 ：WGAN的损失函数改为：
  LD=Ex∼pdata[D(x)]−Ez∼pz[D(G(z))] L_D = \mathbb{E}{x \sim p{\text{data}}}[D(x)] - \mathbb{E}{z \sim p_z}[D(G(z))] LD=Ex∼pdata[D(x)]−Ez∼pz[D(G(z))]
  LG=−Ez∼pz[D(G(z))] L_G = -\mathbb{E}{z \sim p_z}[D(G(z))] LG=−Ez∼pz[D(G(z))]
  同时，要求判别器是1-Lipschitz函数，通常通过梯度惩罚（Gradient Penalty）实现。
- 优点：训练更稳定，模式崩塌减少。
多样性促进损失：在生成器损失中添加多样性项，强制生成器覆盖更多模式。

3. 针对不稳定的方法

使用改进的优化器：如Adam优化器，它能自适应调整学习率，比传统SGD更稳定。
学习率调度：动态调整学习率，例如在训练后期降低学习率，避免振荡。
WGAN和LSGAN（Least Squares GAN） ：这些变体通过修改损失函数来稳定训练。LSGAN使用最小二乘损失：
LD=Ex∼pdata[(D(x)−1)2]+Ez∼pz[(D(G(z)))2] L_D = \mathbb{E}{x \sim p{\text{data}}}[(D(x) - 1)^2] + \mathbb{E}{z \sim p_z}[(D(G(z)))^2] LD=Ex∼pdata[(D(x)−1)2]+Ez∼pz[(D(G(z)))2]
LG=Ez∼pz[(D(G(z))−1)2] L_G = \mathbb{E}{z \sim p_z}[(D(G(z)) - 1)^2] LG=Ez∼pz[(D(G(z))−1)2]
这能减少梯度消失问题。
特征匹配（Feature Matching）：让生成器匹配真实数据在判别器中间层的特征统计量，从而平滑训练过程。