概述:为什么需要小波云模型?
年径流序列是一种典型的非线性、非平稳性时间序列,受到气候变化和人类活动的双重影响。传统的时间序列预测方法(如ARIMA模型)在处理这种复杂特性时往往表现不佳。
• 小波分析 的优势:擅长处理非平稳信号,能将径流序列分解为不同时间尺度的子序列(高频细节和低频趋势),从而揭示序列的局部特征和演化规律。
• 云模型 的优势:由李德毅院士提出,是一种能够完美结合随机性和模糊性的模型。它通过期望(Ex)、熵(En)和超熵(He)三个数字特征,定量地描述自然语言中的概念(如"丰水年"、"平水年"、"枯水年"),非常适合处理水文系统的不确定性。
小波云模型的核心思想:将两者的优势结合。先用小波分析将复杂的径流序列"化繁为简",分解为相对平稳的子序列;然后对每个子序列分别建立云预测模型;最后将各子序列的预测结果重构,得到最终的年径流预测值。
预测步骤详解
整个过程可以分为以下六个核心步骤:
步骤一:数据预处理与年径流状态划分
-
数据收集与整理:收集长系列的年径流数据,并进行一致性、可靠性检验。
-
状态划分(概念化):根据历史数据,将年径流划分为不同的状态等级,例如:
• 枯水年 (L1)
• 偏枯年 (L2)
• 平水年 (L3)
• 偏丰年 (L4)
• 丰水年 (L5)
划分标准可以是百分位数法、聚类分析法等。
步骤二:小波分解
-
选择小波基函数:常用的小波基有Daubechies (dbN)、Symlets (symN)等。选择不同的小波基会影响分解效果,通常需要通过对比试验确定最优小波。
-
确定分解层数:分解层数过多会导致信息冗余,过少则无法有效分离不同频率的成分。通常根据数据长度和序列特性确定,一般3~5层。
-
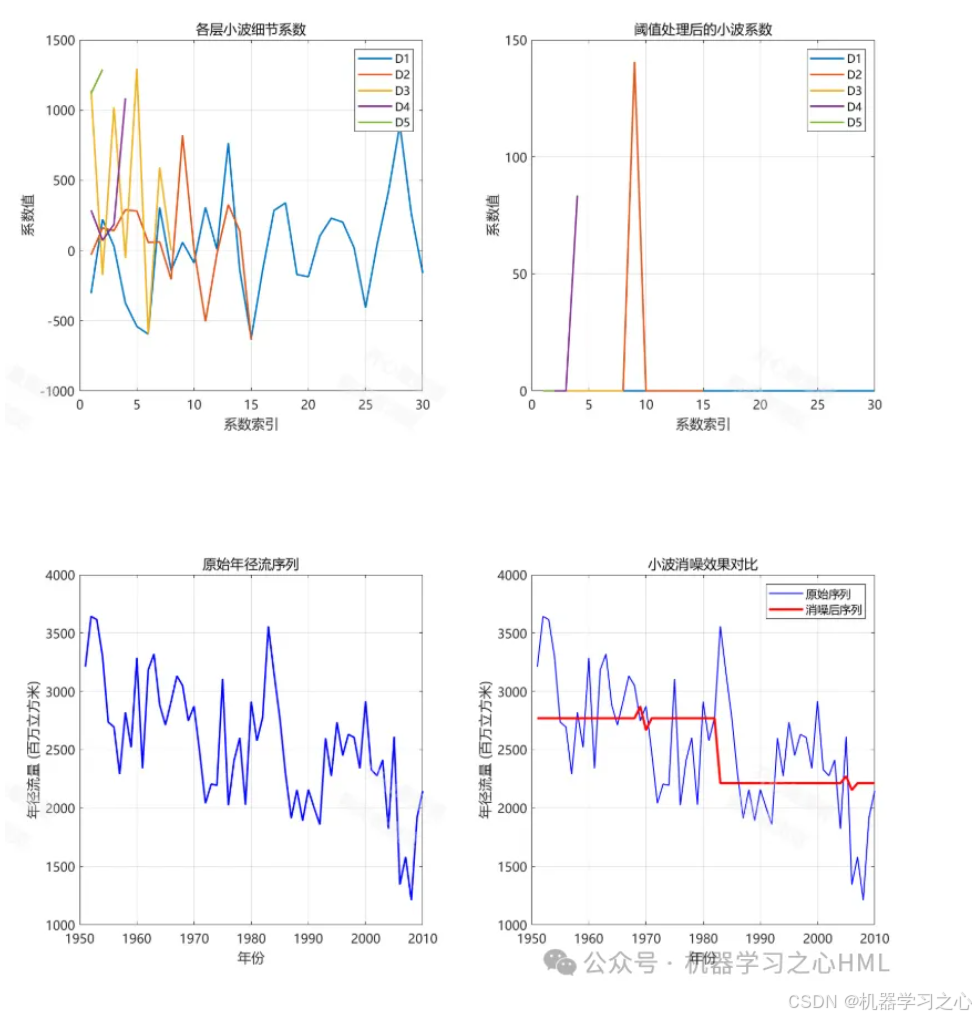
执行分解:将原始年径流序列 分解为一个近似序列 和多个细节序列。
• 近似序列 (A):代表原始序列的低频成分(趋势项)。
• 细节序列 (D1, D2, ...):代表原始序列的高频成分(细节项,如年际波动)。
• 最终,
步骤三:各子序列的云模型建模
对分解后得到的每一个子序列(A, D1, D2, ...)分别建立云模型。
-
确定论域:对于每个子序列,取其历史数据的最大值和最小值作为论域的边界。
-
逆向云发生器:输入每个子序列的历史数据,计算出对应每个径流状态(L1~L5)的云数字特征(Ex, En, He)。
• Ex (期望):概念在论域中的中心值。对于"丰水年"子序列,Ex值较大。
• En (熵):概念的模糊度,反映了该状态可接受的数值范围。
• He (超熵):熵的不确定性度量,反映了云滴的离散程度(厚度)。
至此,每个子序列都拥有了一个"云模型库",描述了该子序列在不同径流状态下的变化规律。
步骤四:基于云推理的子序列预测
这是预测的核心环节。对于待预测年份的每个子序列,进行如下操作:
- 输入条件:以待预测年前若干年(如前3年)的该子序列数据作为条件属性。
- 云推理:
• 将条件属性输入到前一阶段建立的云模型中。
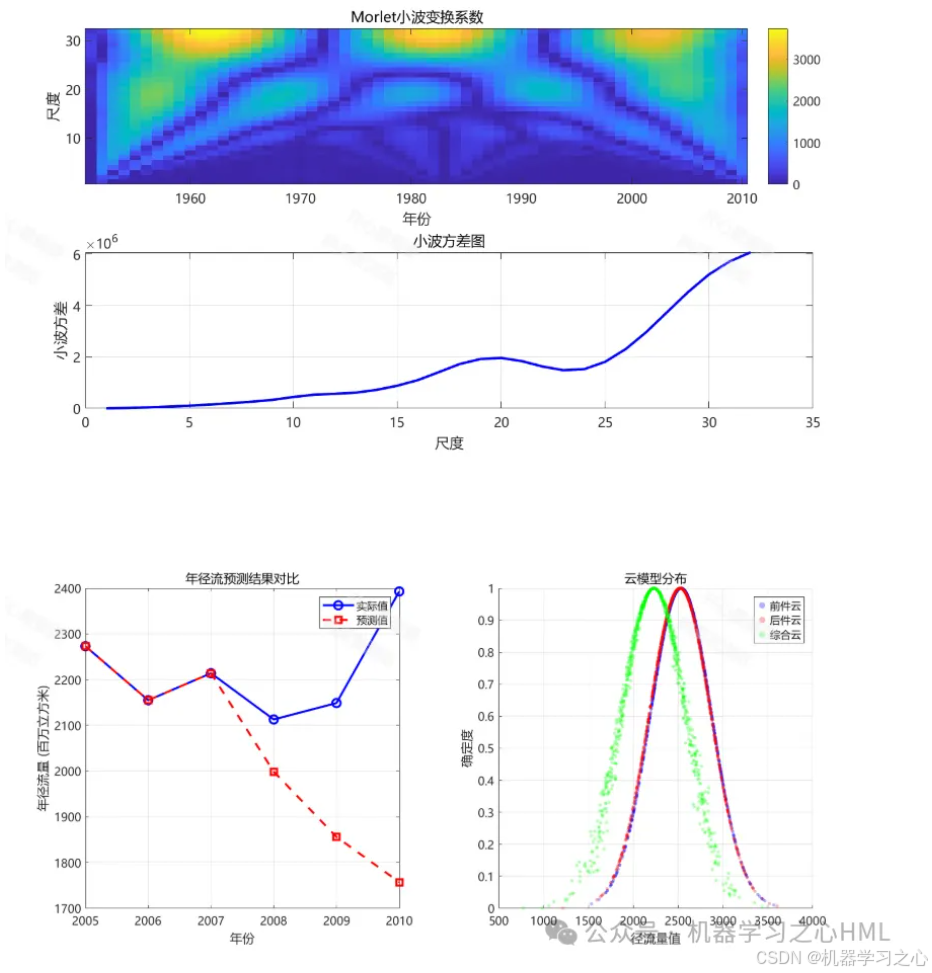
• 通过条件云发生器,计算在给定条件下,待预测年该子序列属于各个状态(L1~L5)的确定度。 - 确定预测状态:选择确定度最高的状态作为该子序列的预测状态。
- 生成预测值:根据预测状态对应的云数字特征(Ex, En, He),通过正向云发生器生成一个具体的、带有不确定性的预测值。可以生成多个云滴,取其期望作为该子序列的确定性预测值。
步骤五:小波重构
将步骤四中得到的所有子序列的预测值进行小波重构,得到最终的归一化年径流预测值。
步骤六:结果分析与评估
- 反归一化:将重构后的预测值反归一化,得到实际的年径流量预测值。
- 模型评估:使用测试集数据,采用以下指标评估模型性能:
• 均方根误差 (RMSE)
• 平均绝对百分比误差 (MAPE)
• 纳什效率系数 (NSE)
• 确定性系数 (R²) - 不确定性分析:由于云模型本身能产生多个云滴,可以据此给出预测值的区间范围(如置信区间),而不仅是一个单点值,这对水资源风险管理至关重要。
优势与挑战
优势: - 处理非平稳性:小波分解有效解决了径流序列的非平稳性问题。
- 描述不确定性:云模型能同时处理随机性和模糊性,预测结果更符合水文现象的物理本质。
- 多尺度分析:能从不同时间尺度上分析径流形成的物理机制,预测信息更丰富。
- 智能性:结合了模糊逻辑和概率统计,具有一定的智能推理能力。
挑战与注意事项: - 参数选择敏感:小波基函数、分解层数、径流状态划分标准等对结果影响较大,需要谨慎选择。
- 计算复杂度:步骤较多,计算量相对较大。
- 数据要求:需要较长系列的历史数据来保证云模型建模的稳定性。
- "维数灾"风险:如果子序列过多,且每个序列的状态划分很细,会导致云推理规则组合爆炸。
总结
基于小波云模型的年径流预测是一种数据驱动与概念驱动相结合的先进方法。它不仅在数学上严谨,更在哲学层面上符合水文系统"确定性"与"不确定性"并存的客观规律。尽管模型构建过程较为复杂,但它在处理年径流这类高度复杂的非线性系统时,展现出了比传统方法更强的适用性和潜力,尤其适合为水资源规划和管理提供带有不确定性信息的决策支持。