单调栈的“降维打击”：从直方图到矩阵——再探「最大矩形」

哈喽，各位，我是前端小L。

在上一篇文章中，我们刚刚经历了一场酣畅淋漓的"封神之战"，用单调栈 O(n) 的优雅姿态，完美解决了"柱状图中最大的矩形"（LC 84）。我们掌握了如何在一次遍历中，确定每个柱子能延伸的左右边界。

今天，我们的战场从"一维"的柱状图，升级到了"二维"的 0/1 矩阵。我们要在这片土地上，圈出那块完全由 1 构成的、面积最大的矩形。你可能会觉得，维度升高，难度必然剧增。但你将惊喜地发现，凭借我们手中已有的"单调栈"利器，配合一点巧妙的"视角转换"，这个问题将应声而解！

力扣 85. 最大矩形

https://leetcode.cn/problems/maximal-rectangle/

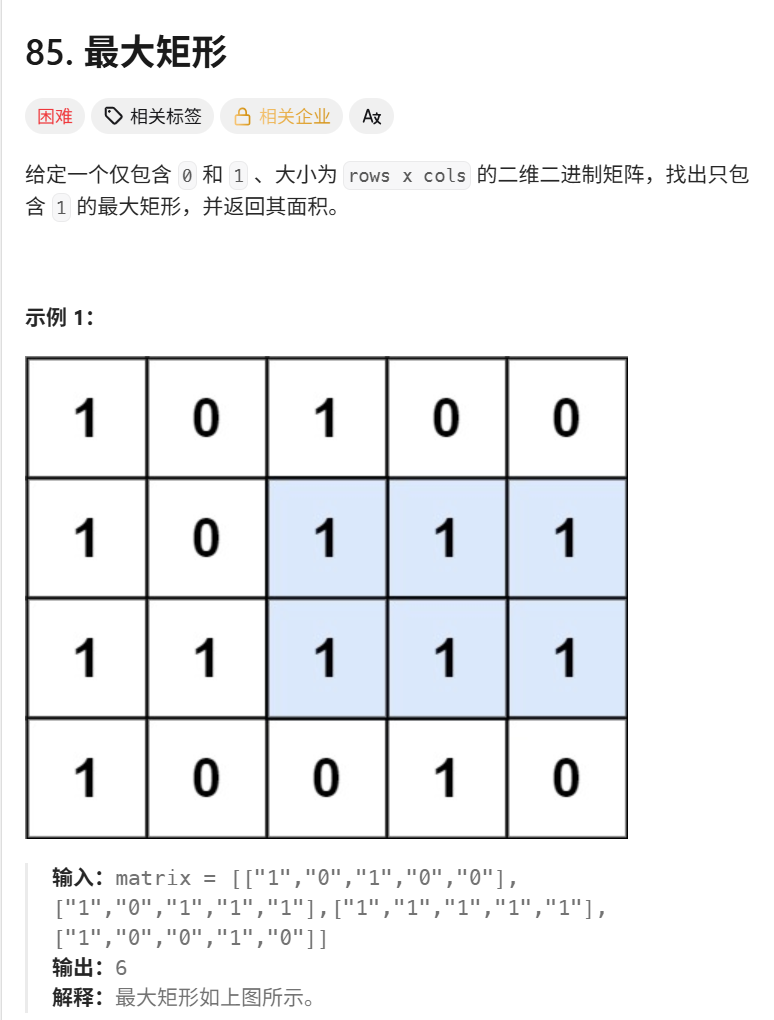
题目分析： 在一个由 0 和 1 组成的二维矩阵中，找到只包含 1 的最大矩形的面积。

与 LC 84 的联系： LC 84 处理的是高度数组构成的直方图。而这个矩阵，看起来和直方图相去甚远。如何建立联系？

"Aha!"时刻 ------ 逐行构建"空中直方图"

关键在于，我们不要试图一次性解决整个二维问题。我们可以逐行扫描 这个矩阵，并将每一行，想象成构建直方图的"地基"。

核心思想： 当我们处理到第 i 行时，我们可以计算出在这一行，以每个位置 j 为底座，向上能延伸的连续 1 的高度是多少。

举个例子： matrix = [ ["1","0","1","0","0"], ["1","0","1","1","1"], <-- 假设我们处理到这一行 (i=1) ["1","1","1","1","1"], ["1","0","0","1","0"] ]

第 0 行 : 高度数组 heights = [1, 0, 1, 0, 0]
第 1 行:
- j=0: matrix[1][0]=='1', 上一行高度 1 -> 新高度 1+1=2
- j=1: matrix[1][1]=='0', 高度中断 -> 新高度 0
- j=2: matrix[1][2]=='1', 上一行高度 1 -> 新高度 1+1=2
- j=3: matrix[1][3]=='1', 上一行高度 0 -> 新高度 0+1=1
- j=4: matrix[1][4]=='1', 上一行高度 0 -> 新高度 0+1=1
- 第 1 行对应的高度数组 heights = [2, 0, 2, 1, 1]

发现了吗？ 对于每一行 i，我们都可以生成一个对应的 heights 数组。而在以第 i 行为底、只包含 1 的所有矩形中，面积最大的那个，就等价于在由 heights 数组构成的直方图中，找到的最大矩形面积！

结论： 我们成功地将一个二维的 (m*n) 矩阵问题，分解成了 m 个一维的 (1*n) 柱状图最大矩形问题！

最终算法：逐行构建直方图 + 复用 LC 84 解法

现在，算法步骤清晰无比：

初始化 maxArea = 0。
创建一个 heights 数组，长度为 n（矩阵的列数），初始全为0。
逐行遍历 矩阵 (从 i = 0 到 m-1)： a. 更新 heights 数组 ：遍历当前行 i 的每一列 j。 * 如果 matrix[i][j] == '1'，则 heights[j] += 1。 * 如果 matrix[i][j] == '0'，则 heights[j] = 0 (高度中断)。 b. 调用 LC 84 解法 ：将当前 heights 数组传入我们上一篇已经写好的 largestRectangleInHistogram 函数，得到当前行的最大矩形面积 currentMax。 c. 更新全局最大值 ：maxArea = max(maxArea, currentMax)。
所有行遍历完毕后，maxArea 就是最终答案。

代码实现 (融合 LC 84 解法)

复制代码

#include <vector>
#include <stack>
#include <algorithm> // for max

using namespace std;

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) {
            return 0;
        }
        int m = matrix.size();
        int n = matrix[0].size();
        
        // heights[j] 表示在当前行i，第j列向上延伸的连续1的高度
        vector<int> heights(n, 0);
        int maxArea = 0;

        for (int i = 0; i < m; ++i) {
            // 1. 更新 heights 数组
            for (int j = 0; j < n; ++j) {
                if (matrix[i][j] == '1') {
                    heights[j] += 1;
                } else {
                    heights[j] = 0;
                }
            }
            // 2. 对当前 heights 数组（直方图）调用 LC 84 的解法
            maxArea = max(maxArea, largestRectangleInHistogram(heights));
        }
        return maxArea;
    }

private:
    // LeetCode 84: 柱状图中最大的矩形 (单调栈解法 - O(n) 时间, O(n) 空间)
    int largestRectangleInHistogram(vector<int>& heights) {
        stack<int> s; // 存储索引的单调递增栈
        heights.push_back(0); // 哨兵
        int n = heights.size();
        int maxArea = 0;
        
        for (int i = 0; i < n; ++i) {
            while (!s.empty() && heights[i] < heights[s.top()]) {
                int h = heights[s.top()];
                s.pop();
                int w = s.empty() ? i : i - s.top() - 1;
                maxArea = max(maxArea, h * w);
            }
            s.push(i);
        }
        heights.pop_back(); // 恢复
        return maxArea;
    }
};

总结：降维打击的威力

今天这道题，是"问题转化"思想的又一次伟大胜利。它雄辩地证明了：

许多高维度的问题，可以通过巧妙的视角转换和预处理，被分解为一系列我们已经掌握解法的低维度子问题。

我们没有尝试发明一个全新的二维单调栈（那会非常复杂），而是：

逐行处理，将注意力集中在一维。
构建高度数组 heights ，将二维的 0/1 信息转化为一维的高度信息。
复用已知模型（LC 84），解决转化后的一维问题。

这种**"降维打击"**的思路，是算法设计中极其宝贵的财富。它要求我们不仅要会解决单个问题，更要善于发现不同问题之间的联系，建立起自己的"模型库 "，并在遇到新挑战时，尝试将其"归约"到已知的模型上。

咱们下期见。