数据结构算法学习：LeetCode热题100-图论篇（岛屿数量、腐烂的橘子、课程表、实现 Trie (前缀树)）

文章目录

• 简介
• [200. 岛屿数量](#200. 岛屿数量)
• • 递归-深度优先搜索
  • 广度优先搜索
  • 并查集
• [994. 腐烂的橘子](#994. 腐烂的橘子)
• [207. 课程表](#207. 课程表)
• • 着色法-DFS
  • 拓扑排序-BFS
• [208. 实现 Trie (前缀树)](#208. 实现 Trie (前缀树))
• 个人学习总结

简介

本篇博客聚焦于 LeetCode 热题 100 中的图论经典问题，包括"岛屿数量"、"腐烂的橘子"、"课程表"以及"实现 Trie (前缀树)"。这些问题是图算法思想的绝佳实践，涵盖了从网格遍历、连通性判断，到有向图的环路检测，再到高效字符串处理结构等多个核心场景。通过本文，你将深入理解并掌握深度优先搜索（DFS）、广度优先搜索（BFS）、并查集以及拓扑排序等关键算法的实战应用，从而在面对复杂的图论问题时，能够迅速定位模型并选择最优解法。

200. 岛屿数量

问题描述

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例：

输入：grid = [
  ['1','1','0','0','0'],
  ['1','1','0','0','0'],
  ['0','0','1','0','0'],
  ['0','0','0','1','1']
]
输出：3

标签提示： BFS、DFS、矩阵、并查集

递归-深度优先搜索

解题思想

采用"洪水填充"或"感染"的思想。每当遇到一个未被访问的陆地（'1'），就发现了一个新岛屿。然后，通过深度优先搜索，将这个岛屿的所有相连陆地都"淹没"（标记为已访问，如改为 '0'）。整个网格中，启动"淹没"的次数就是岛屿的总数。

解题步骤

1. 遍历网格中的每一个单元格。
2. 如果当前单元格是陆地（'1'），则岛屿数量加一。
3. 从该单元格开始进行 DFS 搜索，将其自身及所有上下左右相连的陆地单元格都标记为 '0'。
4. 重复上述过程，直到遍历完整个网格。

实现代码

class Solution {
    // 利用深度优先搜索，深搜的次数作为岛屿数
    // 1.遇到1，进入搜索，往四处探索，到达边界或0则结束
    // 2.将所有元素变为0，边深搜边将1改为0
    public void dfs(char[][] grid, int r, int c){
        int numr = grid.length;
        int numc = grid[0].length;
        // 边界判定
        if(r < 0 || r >= numr || c < 0 || c >= numc || grid[r][c] == '0'){
            return ;
        }
        // 更改值
        grid[r][c] = '0';
        // 递归
        dfs(grid, r + 1, c);
        dfs(grid, r, c - 1);
        dfs(grid, r - 1, c);
        dfs(grid, r, c + 1);
    }
    public int numIslands(char[][] grid) {
        int numr = grid.length;
        int numc = grid[0].length;
        int ans = 0;
        for(int r = 0; r < numr; r ++){
            for(int c = 0; c < numc; c ++){
                if(grid[r][c] == '1'){
                    ans ++;
                    dfs(grid, r, c);
                    
                }
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度: O(M * N)
  其中 M 和 N 分别是网格的行数和列数。每个单元格最多被访问一次。
• 空间复杂度: O(M * N)
  最坏情况下（当整个网格都是陆地时），递归调用栈的深度可能达到 M * N。

广度优先搜索

解题思想

与 DFS 思想类似，同样是"洪水填充"。区别在于，当发现一个新岛屿后，使用广度优先搜索（借助队列）来逐层"淹没"整个岛屿，而不是用递归。

解题步骤

1. 遍历网格中的每一个单元格。
2. 如果当前单元格是陆地（'1'），则岛屿数量加一。
3. 将该单元格标记为 '0'，并将其坐标加入队列。
4. 循环处理队列，每次从队列中取出一个单元格，并将其所有未被访问的陆地邻居标记为 '0' 后加入队列，直到队列为空。
5. 重复上述过程，直到遍历完整个网格。

实现代码

class Solution {
    // 利用BFS完成搜索，也是洪水法，边遍历边把岛屿淹掉
    // 进行几次BFS，便是有几个岛屿
    // 将二维数组展成一维数组，然后队列就记录对应的一维数组位置
        
    public int numIslands(char[][] grid) {
        int numr = grid.length;
        int numc = grid[0].length;
        int ans = 0;
        Queue<Integer> queue = new LinkedList<Integer>();
        for(int r = 0; r < numr; r ++){
            for(int c = 0; c < numc; c ++){
                if(grid[r][c] == '1'){
                    ans ++;
                    grid[r][c] = '0';
                    queue.offer(r * numc + c);
                    while(!queue.isEmpty()){
                        int id = queue.remove();
                        // 还原行列
                        int row = id / numc;
                        int col = id % numc;
                        // 开始深搜，向四周扩
                        if(row + 1 < numr && grid[row + 1][col] == '1'){
                            grid[row + 1][col] = '0';
                            queue.offer((row + 1) * numc + col);
                        }
                        if(col - 1 >= 0 && grid[row][col - 1] == '1'){
                            grid[row][col - 1] = '0';
                            queue.offer(row * numc + col - 1);
                        }
                        if(row - 1 >= 0 && grid[row - 1][col] == '1'){
                            grid[row - 1][col] = '0';
                            queue.offer((row - 1) * numc + col);
                        }
                        if(col + 1 < numc && grid[row][col + 1] == '1'){
                            grid[row][col + 1] = '0';
                            queue.offer(row * numc + col + 1);
                        }
                    }
                }
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度: O(M * N)
  每个单元格最多被访问和入队一次。
• 空间复杂度: O(M * N)
  最坏情况下，队列中可能需要存储 M * N 个单元格。

并查集

解题思想

将每个陆地单元格（'1'）看作一个独立的元素，每个元素初始时自成一个集合（即一个岛屿）。遍历网格，当发现相邻的两个陆地单元格时，就将它们所在的集合进行合并。最终，独立集合的数量就是岛屿的数量。

解题步骤

1. 初始化并查集。遍历网格，为每个 '1' 创建一个独立的集合，并记录初始的岛屿数量。
2. 再次遍历网格，对于每个 '1'，检查其右边和下边的邻居。
3. 如果邻居也是 '1'，则将当前单元格与邻居进行 union（合并）操作。如果合并成功（说明它们原属不同集合），则将总岛屿数量减一。
4. 遍历结束后，剩下的岛屿数量即为最终结果。

实现代码

class Solution {
    // 并查集求解
    // 需要一个并查集类(找集合老大、合并集合功能)
    class UnionFind{
        // 集合数
        int count;
        // 通过记录集合标识（老大）
        int[] parent;
        // 记录集合的秩，当前数量
        int[] rank;
        // 初始化并查集
        public UnionFind(char[][] grid){
            count = 0;
            int rows = grid.length;
            int cols = grid[0].length;
            int size = rows * cols;
            parent = new int[size];
            rank = new int[size];
            for(int i = 0; i < rows; i ++){
                for(int j = 0; j < cols; j ++){
                    if(grid[i][j] == '1'){
                        int n = i * cols + j;
                        parent[n] = n;
                        rank[n] = 1;
                        count ++;
                    }
                }
            }
        }
        // 寻找集合标识（老大）
        public int find(int x){
            if(parent[x] != x){
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }
        // 合并集合
        public void union(int x, int y){
            int parentx = find(x);
            int parenty = find(y);
            // 同一个集合，不操作
            if(parentx == parenty){
                return ;
            }
            // 不在同一个集合，得合并
            if(rank[parentx] > rank[parenty]){
                parent[parenty] = parentx;
                rank[parentx] += rank[parenty];
                -- count;
            }else{
                parent[parentx] = parenty;
                rank[parenty] += rank[parentx];
                -- count;
            }
        }
        // 得到结果
        public int getCount(){
            return count;
        }
    }
    public int numIslands(char[][] grid) {
        if(grid == null || grid.length == 0){
            return 0;
        }
        int rows = grid.length;
        int cols = grid[0].length;
        // 初始化并查集
        UnionFind uf = new UnionFind(grid);
        // 开始遍历，归并集合
        for(int i = 0; i < rows; i ++){
            for(int j = 0; j < cols; j ++){
                if(grid[i][j] == '1'){
                    // 然后右和下的去合并即可
                    if(j + 1 < cols && grid[i][j + 1] == '1'){
                        uf.union(i * cols + j,i * cols + j + 1);
                    }
                    if(i + 1 < rows && grid[i + 1][j] == '1'){
                        uf.union(i * cols + j, (i + 1) * cols + j);
                    }
                }
            }
        }
        return uf.getCount();
    }
}

复杂度分析

• 时间复杂度: O(M * N * α(M * N))
  其中 α 是阿克曼函数的反函数，增长极慢，可视为常数。因此，时间复杂度近似为 O(M * N)。
• 空间复杂度: O(M * N)
  需要 parent 和 rank 数组来存储 M * N 个元素的信息。

994. 腐烂的橘子

问题描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；

值 1 代表新鲜橘子；

值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例：

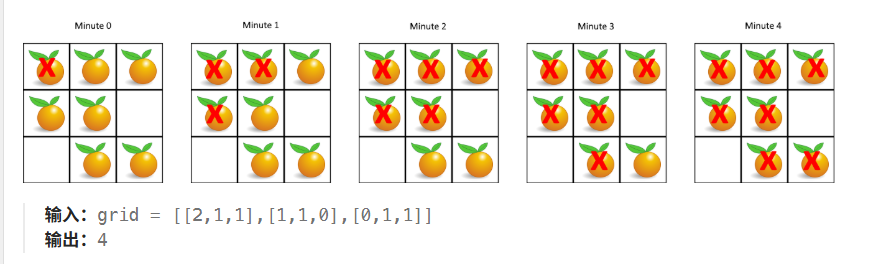
标签提示： BFS、矩阵

解题思想

这道题的本质是一个扩散过程的模拟。想象一下，每个腐烂的橘子都是一个病毒源头，病毒以每分钟一格的速度向四周扩散。这完美契合了广度优先搜索（BFS） 的核心思想------逐层扩展。

我们将所有初始的腐烂橘子看作是第 0 层的节点。它们在第一分钟会感染所有相邻的新鲜橘子，这些被感染的橘子就构成了第 1 层。接着，第 1 层的橘子会在下一分钟去感染它们相邻的橘子，形成第 2 层......

因此，整个过程就像水波纹一样，一圈一圈地向外扩散。BFS 每向外扩展一层，就代表时间过去了一分钟。我们总共扩展了多少层，就是最终需要的分钟数。

解题步骤

1. 准备阶段：收集初始信息
   • 首先，遍历整个网格，完成两件事：
     • 将所有初始腐烂的橘子（病毒源头）放入一个队列中，作为 BFS 的起点。
     • 统计新鲜橘子的总数，这是我们判断是否成功的最终标准。
2. 模拟阶段：逐分钟扩散
   • 开始一个循环，模拟时间的流逝。循环的条件是：队列不为空（还有橘子能传播）且 新鲜橘子数量大于 0（还有橘子需要被感染）。
   • 在每一轮循环中（代表一分钟）：
     • 处理当前队列中所有的橘子（即当前这一层的所有感染源）。
     • 让它们去感染四周的新鲜橘子。
     • 每成功感染一个，就将新鲜橘子总数减一，并将这个新腐烂的橘子加入队列，让它成为下一分钟的感染源。
     • 当这一轮处理完毕，时间加一。
3. 收尾阶段：判断结果
   • 当循环结束后，检查新鲜橘子的总数。
   • 如果总数为 0，说明所有橘子都被成功感染，返回记录的总分钟数。
   • 如果总数不为 0，说明有橘子因为被空格隔开，永远无法被感染，返回 -1。

实现代码

class Solution {
    // 每个烂橘子可以每分钟向四周传染-广搜的味道，被感染的也会在下一分钟向四周传染
    // 利用队列存储烂橘子的坐标，然后开始出队感染，并将新感染的加入队列，往复
    public int orangesRotting(int[][] grid) {
        // 初始化，维度和队列(存储坐标、数组)
        int rows = grid.length;
        int cols = grid[0].length;
        Queue<int[]> queue = new LinkedList<int[]>();
        // 记录新鲜橘子的数量
        int fresh = 0;
        // 遍历网格，找到所有初始烂橘子，和新鲜橘子数量
        for(int r = 0; r < rows; r ++){
            for(int c = 0; c <cols; c ++){
                if(grid[r][c] == 2){
                    queue.offer(new int[]{r,c});
                }else if(grid[r][c] == 1){
                    fresh ++;
                }
            }
        }
        // 如果fresh = 0, 不用污染
        if(fresh == 0){
            return 0;
        }
        // 设置四个方向的数据结构，和时间
        int[][] directions = new int[][]{{-1,0}, {1,0}, {0,-1}, {0,1}};
        int ans = 0;
        // 开始BFS
        while(!queue.isEmpty() && fresh > 0){
            // 记录此时的烂橘子数量(当前时刻的，还未感染周围的)
            int size = queue.size();
            // 开始感染
            for(int i = 0; i < size; i ++){
                int[] point = queue.poll();
                int r = point[0];
                int c = point[1];
                // 开始感染邻居
                for(int[] dir : directions){
                    int nr = r + dir[0];
                    int nc = c + dir[1];
                    // 检查是否为好橘子
                    if(nr >= 0 && nr < rows && nc >= 0 && nc < cols && grid[nr][nc] == 1){
                        grid[nr][nc] = 2;
                        queue.offer(new int[]{nr,nc});
                        fresh --;
                    }
                }
            }
            ans ++;
        }
        if(fresh == 0){
            return ans;
        }else{
            return -1;
        }
    }
}

复杂度分析

• 时间复杂度：O(M * N)
  其中 M 和 N 是网格的行数和列数。在最坏情况下，我们需要遍历网格中的每一个单元格数次（初始扫描 + BFS 访问）。这是解决该问题的理论下限。
• 空间复杂度：O(M * N)
  空间主要取决于队列。在最坏情况下（例如，网格中大部分或全部是腐烂橘子），队列可能需要存储 O(M * N) 个坐标。

207. 课程表

问题描述

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

标签提示： DFS、BFS、图、拓扑排序

着色法-DFS

解题思想

这种思想可以比喻为 "在一条学习路径上探路，并检查是否绕回了起点"。

我们从任意一门未访问的课程开始，沿着先修关系进行深度优先搜索。在搜索过程中，我们为每个课程标记一个状态：

• 未访问：还没开始探查这门课。
• 正在访问：当前正在这条学习路径上，刚刚到达了这门课。
• 已访问：已经完整地探查过这门课，并确认从它出发不会形成环，是安全的。

如果在探查过程中，我们遇到了一门状态为 "正在访问" 的课程，就意味着我们回到了当前路径上的某一点，即发现了环。

解题步骤

1. 构建图：使用邻接表来表示课程之间的先修关系。
2. 初始化状态：创建一个状态数组，所有课程初始状态为"未访问"。
3. 遍历并深搜：遍历所有课程。对于每个"未访问"的课程，启动 DFS 进行环检测。
4. DFS 环检测：
   • 进入一个节点时，将其标记为 "正在访问"。
   • 递归访问其所有邻居。如果在邻居中发现 "正在访问" 的节点，则返回 true（表示有环）。
   • 如果所有邻居都安全，则将该节点标记为 "已访问"，并返回 false（表示无环）。
5. 得出结论：如果任何一次 DFS 检测到环，则整个课程计划不可行。如果所有节点都探查完毕且未发现环，则计划可行。

实现代码

class Solution {
    // 其实是判断一个图是否存在有向无环图的问题（拓扑排序）
    // 深度优先，路径着色法，遍历过程中，检查是否存在环
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 1.构建邻接表（图）
        List<List<Integer>> adjList = new ArrayList<>();
        for(int i = 0; i < numCourses; i ++){
            adjList.add(new ArrayList<>());
        }
        for(int[] pre : prerequisites){
            adjList.get(pre[1]).add(pre[0]);
        }
        // 2.创建状态数组，用来记录当前节点的访问状态
        int[] status = new int[numCourses];
        // 3.遍历所有节点，对每个节点进行深搜（判断是否有环）
        for(int i = 0; i < numCourses; i ++){
            if(status[i] == 0){
                if(dfs(i, adjList, status)){
                    return false;
                }
            }
        }
        return true;

        
    }
    // 4.深搜当前节点的所有邻接节点，判断是否有环
    public boolean dfs(int node, List<List<Integer>> adjList, int[] status){
        // status 为 1，为正在访问，有环
        if(status[node] == 1){
            return true;
        }
        // status 为 2，已经访问过了为安全节点
        if(status[node] == 2){
            return false;
        }
        // 0，为访问过，设置为访问
        status[node] = 1;
        // 然后开始深搜邻居节点
        for(int neighbor : adjList.get(node)){
            if(dfs(neighbor, adjList, status)){
                return true;
            }
        }
        // 访问完之后
        status[node] = 2;
        return false;
    }
}

复杂度分析

• 时间复杂度：O(V + E)
  V 为课程数（numCourses），E 为先修关系的数量（prerequisites.length）。我们需要访问每个节点和每条边一次。
• 空间复杂度：O(V + E)
  邻接表需要 O(V + E) 的空间，状态数组和递归调用栈在最坏情况下需要 O(V) 的空间。

拓扑排序-BFS

解题思想

这种思想更贴近现实的选课策略："每学期都优先上那些没有先修要求的课"。

我们统计每门课有多少个先修要求（即"入度"）。入度为 0 的课，就是当前可以上的课。我们把这些课加入一个队列，然后开始"上课"。

每"上完"一门课，它就不再是后续课程的先修课了，所以我们将所有依赖它的课程的入度减 1。如果某门课的入度因此减到了 0，它就变成了新的"可上课程"，我们也将它加入队列。

这个过程本质上就是 拓扑排序。如果最终所有课程都能被上完，说明图中没有环。

解题步骤

1. 构建图与入度表：使用邻接表表示图，并创建一个数组来记录每门课的入度。
2. 初始化队列：遍历所有课程，将所有入度为 0 的课程加入队列。
3. 开始 BFS（拓扑排序）：
   • 当队列不为空时，从队列中取出一个课程，表示"上完"这门课，并计数。
   • 遍历它的所有后续课程，将它们的入度减 1。
   • 如果某门后续课程的入度减为 0，则将其加入队列。
4. 得出结论：循环结束后，比较"已上完的课程数"和"总课程数"。如果两者相等，说明所有课程都能完成，图无环；否则，说明有环。

实现代码

class Solution {
    // 其实是判断一个图是否存在有向无环图的问题（拓扑排序）
    // 利用BFS，得记录节点的入度，从入度为0的开始广搜，直到搜索结束判断是否还存在未搜节点
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 1.构建领接表和入度数组
        List<List<Integer>> adjList = new ArrayList<>();
        int[] inDegree = new int[numCourses];
        for(int i = 0; i < numCourses; i++){
            adjList.add(new ArrayList<>());
        }
        for(int[] pre : prerequisites){
            // pre[0]为想修，pre[1]为前置课程
            int course = pre[0];
            int preCourse = pre[1];
            // 添加到邻接表
            adjList.get(preCourse).add(course);
            // course的入度加1
            inDegree[course] ++;
        }
        // 2.将入度为0的节点加入队列
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0; i < numCourses; i ++){
            if(inDegree[i] == 0){
                queue.offer(i);
            }
        }
        // 3.BFS,拓扑排序
        // 记录能够修的课程
        int count = 0;
        while(!queue.isEmpty()){
            int currCourse = queue.poll();
            count ++;
            for(int neighbor : adjList.get(currCourse)){
                inDegree[neighbor] --;
                // 如果入度减为零，入队
                if(inDegree[neighbor] == 0){
                    queue.offer(neighbor);
                }
            }
        }
        // 4.结果判定
        return numCourses == count;
    }
}

复杂度分析

• 时间复杂度：O(V + E)
  我们需要遍历所有节点和边来构建图和进行 BFS。
• 空间复杂度：O(V + E)
  邻接表、入度数组和队列在最坏情况下都需要 O(V + E) 的空间。

208. 实现 Trie (前缀树)

问题描述

Trie（发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补全和拼写检查。

请你实现 Trie 类：

• Trie() 初始化前缀树对象。
• void insert(String word) 向前缀树中插入字符串 word 。
• boolean search(String word) 如果字符串 word 在前缀树中，返回
  true（即，在检索之前已经插入）；否则，返回 false 。
• boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

标签提示： 设计、字典树、哈希表

解题思想

Trie（前缀树）是一种专门为高效处理字符串前缀问题而设计的树形数据结构。其核心思想是 "共享公共前缀，以空间换时间"。

想象一下，我们要存储 "app", "apple", "apply"。在普通列表中它们是独立的，但在 Trie 中，它们会共享从根节点到 "a" -> "p" -> "p" 的这条公共路径。

• 路径即前缀：树中的每一条从根到节点的路径，都代表一个前缀。
• 节点设计：每个节点只需回答两个问题：
  • 我的下一个字符有哪些？（通过一个 Map 实现，指向子节点）
  • 我这里是不是一个单词的结尾？（通过一个 boolean 标志实现）

通过这种结构，字符串的查询和插入操作，被高效地转化为了在树上的路径遍历。

解题步骤

1. 设计节点（蓝图）

   首先定义 Trie 的基本单元------节点。每个节点包含两部分：

   • 一个 Map，用于存储指向其所有子节点的链接。
   • 一个 boolean 标志，用于标记从根节点到此是否构成一个完整的单词。

2. 初始化 Trie（地基）

   创建一个 Trie 类，它持有一个唯一的根节点。这个根节点是所有操作的起点，本身不存储任何字符。

3. 插入单词（铺设路径）

   • 从根节点出发，遍历单词的每个字符。
   • 对于每个字符，检查当前节点是否存在对应的路径。
   • 如果不存在，就创建一个新节点并建立连接。
   • 遍历完成后，在最后一个节点上打上"单词结尾"的标记。

4. 查找单词（寻找终点）

   • 从根节点出发，沿着单词的字符路径查找。
   • 如果路径中途断裂，说明单词不存在。
   • 如果能完整走完路径，还需检查终点是否被标记为"单词结尾"。只有被标记，才是一个完整的单词。

5. 前缀查找（确认方向）

   • 过程与查找类似，但更简单。
   • 只需从根节点出发，沿着前缀的字符路径查找。
   • 只要能完整走完路径，就说明该前缀存在，无需关心终点是否被标记。

实现代码

class Trie {

    // 节点类
    class TrieNode{
        // 通过map来存储26个字母，作为节点信息
        Map<Character, TrieNode> children;
        // 标记该节点是否为单词的结尾
        boolean isEnd;
        // 初始化
        public TrieNode(){
            children = new HashMap<>();
            isEnd = false;
        }
    }

    // trie的根节点，仅作为入口，不存储信息
    private final TrieNode root;
    // 初始化
    public Trie(){
        root = new TrieNode();
    }
    
    public void insert(String word) {
        TrieNode node = root;
        for(char c : word.toCharArray()){
            if(!node.children.containsKey(c)){
                // 不存在则创建新节点
                node.children.put(c, new TrieNode());
            }
            // 移动到下一个节点
            node = node.children.get(c);
        }
        // 设置单词结尾
        node.isEnd = true;
    }
    
    public boolean search(String word) {
        TrieNode node = root;
        for(char c : word.toCharArray()){
            if(!node.children.containsKey(c)){
                return false;
            }
            node = node.children.get(c);
        }
        return node.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        TrieNode node = root;
        for(char c : prefix.toCharArray()){
            if(!node.children.containsKey(c)){
                return false;
            }
            node = node.children.get(c);
        }
        return true;
    }
}

复杂度分析

• 时间复杂度：O(L)
  其中 L 是操作的单词或前缀的长度。所有三个方法（insert, search, startsWith）都只需对字符串进行一次遍历。
• 空间复杂度：O(N * L)
  其中 N 是插入的单词总数，L 是单词的平均长度。在最坏情况下（所有单词无公共前缀），需要为每个字符创建一个新节点。

个人学习总结

通过攻克这四道经典的图论问题，我最大的收获是学会了如何"看透"问题的本质，并为其匹配最合适的算法思想。

• 网格即图，遍历是根本："岛屿数量"和"腐烂的橘子"让我深刻理解了 DFS/BFS 在矩阵（隐式图）中的应用。"岛屿数量"是典型的连通性问题，DFS/BFS 的"洪水填充"思想是解题利器。而"腐烂的橘子"则巧妙地运用了多源 BFS，通过队列的层级遍历来模拟时间的流逝，这种思想在解决最短路径或最少步数问题时极具通用性。
• 有向图的核心是环："课程表"问题则是有向图处理的典范。DFS 的"路径着色法"和 BFS 的"拓扑排序"分别从"深度探索"和"广度剥离"两个角度解决了环路检测问题。这让我明白，同一个问题可以有不同的切入视角，选择哪种方法取决于具体场景和性能考量。
• 专用结构的威力："实现 Trie"让我认识到，高效的算法往往依赖于精巧的数据结构设计。Trie 通过共享前缀，将字符串问题转化为树上的路径查找，是"空间换时间"思想的绝佳体现。它提醒我，除了掌握通用算法，理解特定场景下的专用数据结构同样重要。

总而言之，图论的学习核心在于：识别模型（是网格、依赖图还是其他？）、选择思想（是深度优先、广度优先还是集合合并？）、精准实现。这次学习不仅让我掌握了几个"解题模板"，更重要的是培养了我对问题进行抽象和建模的能力。