深度学习中的两个不确定性

偶然不确定性（Aleatoric Uncertainty，AU）

偶然不确定性又称为数据不确定性 ，是由于观测数据本身的噪声产生的（如人脸图像模糊、标注框边缘不准确、医疗图像采集设备噪声等）。

这类不确定性是数据固有 的特性，即使获取更多的观测样本，也无法降低 。

偶然不确定性通常反映输入数据中难以避免的随机扰动，它会在模型预测结果中累积体现出来。

认知不确定性（Epistemic Uncertainty，EU）

认知不确定性又称为模型不确定性 ，来源于模型结构、参数以及训练数据分布的不完善。

当模型训练数据不足、参数未充分学习或模型结构不合理时，模型对输入样本的预测会产生偏差，从而体现为认知不确定性。

与偶然不确定性不同，认知不确定性是可以通过增加训练样本数量或改进模型结构 而降低的。

例如，当输入样本位于训练数据分布之外（out-of-distribution, OOD）时，模型往往会表现出较高的认知不确定性。

Monte-Carlo Dropout（蒙特卡罗 Dropout）

Monte-Carlo Dropout（简称 MC Dropout）由 Gal 和 Ghahramani 于 2016 年提出，论文为：

Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning (ICML 2016)

其核心思想是：通过在测试阶段保持 Dropout 激活状态，对同一输入样本进行多次随机前向传播，从而获得多个不同的输出结果。

由于每次 Dropout 的神经元激活不同，相当于从模型参数的分布中进行采样，因此可以近似模拟贝叶斯神经网络的采样过程。

理论原理

对于一个模型的输出结果，我们希望得到其方差来估计模型不确定性（尤其是认知不确定性）。

但由于训练好的模型参数是固定的，单次预测无法计算方差。

若我们能对同一输入样本进行 TTT 次预测，并且每次的预测结果各不相同，那么就可以计算输出的方差：

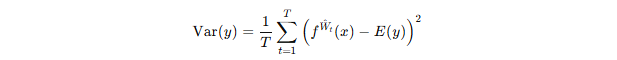
其中：

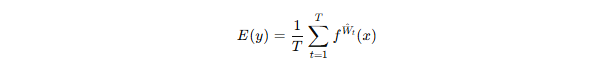
在此过程中，Dropout 起到了近似参数采样的作用。

例如，当 dropout rate = 0.5 时，意味着每个神经元有 50% 的概率被丢弃，这相当于在测试阶段对模型参数进行伯努利分布采样。

因此，通过在测试时保持 Dropout 开启，并进行多次前向传播，我们即可得到模型输出分布的估计，从而估计模型不确定性。

估计不确定性

我们估计不确定性的目的是衡量模型对预测输出的信心程度 。

由于输入数据本身含有偶然不确定性，而模型参数学习不足又带来认知不确定性，因此模型预测输出的不确定性通常是二者的综合反映。

估计的方法可采用 Monte-Carlo Dropout，通过重复预测计算输出分布的均值与方差，进而同时捕获数据噪声与模型参数带来的不确定性。

对于回归问题，不确定性可以用输出值的方差来表示：

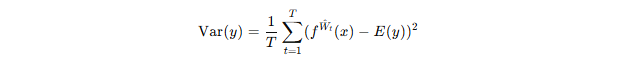
其中：

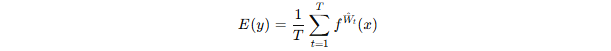
方差越大，说明模型对该样本的预测越不稳定、不自信；方差越小，则说明模型的预测较为确定。

利用不确定性训练模型

估计出模型不确定性后，我们不仅可以将其作为模型置信度的度量指标，还可以在训练过程中利用不确定性信息 ，提高模型的稳健性和泛化能力。

下面分别介绍在回归任务与分类任务中的常见做法。

（1）回归任务中的不确定性建模

在回归问题中，模型通常同时输出目标的均值与方差：

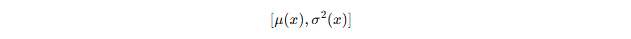
其中，为预测均值，为预测的不确定性（方差）。

基于最大似然推导，可得到以下损失函数：

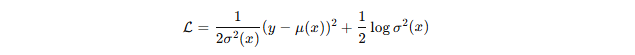
第一项是带权重的均方误差，表示预测与真实值的偏差；
第二项为正则化项，防止模型过度放大方差。

直观地看：

对高噪声样本（大），模型降低其权重；
对低噪声样本（小），模型更加信任其标签；
因此，模型能自动学习数据中噪声的不确定性结构，提高整体鲁棒性。

该思想来自 Kendall 和 Gal 在 2017 年的论文：

What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? (NIPS 2017)

（2）分类任务中的不确定性建模

在分类任务中，模型输出类别概率分布。

若使用 MC Dropout 进行 T 次预测，则可得到 T 个不同的概率分布：

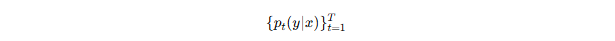
最终平均预测为：

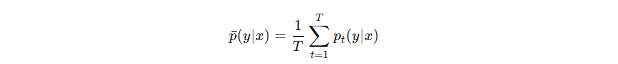
模型的不确定性可用熵（Entropy）表示：

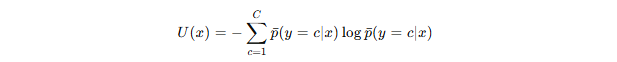
熵值越大，模型越不确定。

此外，可利用**互信息（Mutual Information, MI）**分离认知与偶然不确定性：

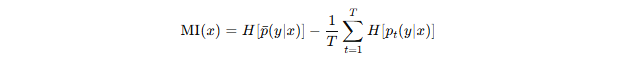
其中：

：总体预测熵（总不确定性）；
平均样本熵：偶然不确定性；
两者差值即认知不确定性。

（3）不确定性在半监督与主动学习中的应用

半监督学习：利用不确定性筛选高置信度样本生成伪标签，或对高不确定样本施加一致性约束；
主动学习：高不确定性样本通常信息量更大，可优先选择进行人工标注；
医学影像分析：可生成不确定性热力图，辅助医生评估模型分割结果的可靠性与风险区域。

总结与展望

深度学习中的不确定性主要分为偶然不确定性 和认知不确定性 ，分别对应于数据噪声与模型参数的不确定来源。

通过 Monte-Carlo Dropout 等方法，可以在不改变网络结构的前提下，对模型输出进行多次采样估计，从而量化预测结果的置信度。

不确定性不仅是模型可靠性的重要指标，也可作为训练信号，引导模型关注高置信度区域或自适应调整样本权重。

未来研究中，不确定性估计将在半监督学习、主动学习、医学影像分析以及可信AI系统中发挥越来越重要的作用，为深度学习模型提供更加稳定、透明与可解释的决策依据。