"你知道 0.1+0.2 不等于 0.3 吧?那我再问一个:为什么 0.1+0.1 又等于 0.2?"
面试现场,当面试官抛出这个问题时,小林心里咯噔一下 ------ 他背过 "0.1 二进制无法精确存储" 的结论,却从没琢磨过 "两个不精确的 0.1 相加,为啥能得到精确的 0.2"。支支吾吾半天没说清,这场面试最终以 "再联系" 收尾。
Java中测试效果如下:

其实这道题的核心,不是 "记结论",而是搞懂IEEE 754 双精度浮点数的存储规则------ 所有 "看似矛盾" 的加法结果,都藏在 "符号位、指数位、尾数位" 这三部分里。
一、先搞懂底层:计算机怎么存 0.1?(IEEE 754 双精度规则)
我们平时用的 "十进制小数",计算机要先转成 "二进制小数",再按 IEEE 754 双精度(Java 的 double、Python 的 float 默认类型)规则存储。双精度共 64 位,分三部分:
- 符号位(1 位) :0 正 1 负,0.1 是正数,所以符号位为 0;
- 指数位(11 位) :用 "偏移值 1023" 表示指数,比如指数是 - 4,实际存储的是 1023-4=1019;
- 尾数位(52 位) :存储二进制小数的 "有效数字",但有个关键规则 ------ 二进制小数会先转成 "1.xxxxxx×2^e" 的科学计数法(类似十进制的 1.23×10^2),而 "1." 是默认不存的,只存后面的 "xxxxxx"(52 位,不够补 0,超了舍入)。
那 0.1 转二进制是多少?答案是无限循环小数:
0.1₁₀ = 0.00011001100110011...₂("0011" 无限循环)
按科学计数法转成 "1.xxxx×2^e":
0.000110011...₂ = 1.100110011...₂ × 2^(-4)
这时候对应到 IEEE 754 存储:
- 指数位:-4 + 1023 = 1019(二进制是 01111111011);
- 尾数位:取 "1.xxxx" 后面的 52 位(因为 "1." 不存),但 "0011" 无限循环,所以第 52 位会触发 "舍入"(类似十进制四舍五入),最终尾数位是 "100110011...001101"(中间省略部分是循环的 0011,最后一位因舍入变 1)。
重点来了:0.1 的二进制是无限循环的,所以计算机存储的 0.1,其实是 "舍入后的近似值",不是数学上精确的 0.1。
二、拆解两个加法:为啥结果天差地别?
知道了 "0.1 是近似值",再看两个加法的区别 ------ 核心是 "两个近似值相加后,结果是否能被 IEEE 754 精确存储"。
案例 1:0.1 + 0.1 = 0.2(结果精确)
先看 0.2 的二进制和存储:
0.2₁₀ = 0.001100110011...₂(同样 "0011" 无限循环)
转科学计数法:0.00110011...₂ = 1.100110011...₂ × 2^(-3)
再看两个 "近似 0.1" 相加的过程(二进制):
两个 0.1 的二进制近似值相加 → 0.000110011...₂ + 0.000110011...₂ = 0.00110011...₂
而这个 "相加结果",刚好就是 0.2 的二进制(无限循环的 0.00110011...₂)。更关键的是:
当这个结果按 IEEE 754 存储时,它的 "1.xxxx×2^e" 形式中,"xxxx" 部分的循环长度,刚好能被 52 位尾数位 "完整容纳 + 舍入后无误差"------ 简单说,两个近似的 0.1 相加后,误差刚好抵消,结果刚好是 0.2 的精确存储值。
我们可以用代码验证:
csharp
// Java中打印0.1的实际存储值(不是数学上的0.1)
System.out.println(new BigDecimal(0.1));
// 输出:0.1000000000000000055511151231257827021181583404541015625
// 打印0.1+0.1的实际值
System.out.println(new BigDecimal(0.1).add(new BigDecimal(0.1)));
// 输出:0.200000000000000011102230246251565404236316680908203125
// 打印0.2的实际存储值
System.out.println(new BigDecimal(0.2));
// 输出:0.200000000000000011102230246251565404236316680908203125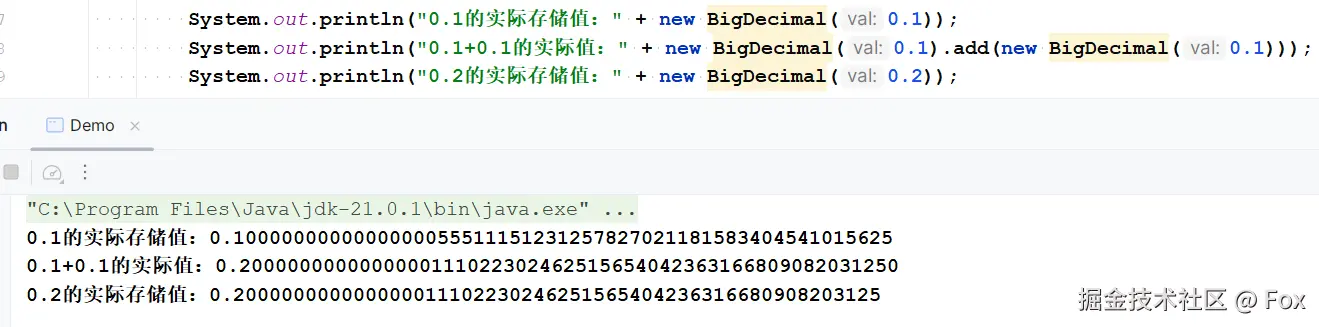
看到了吗?0.1+0.1 的结果,和 0.2 的存储值完全一样 ------ 所以计算机判定 "0.1+0.1=0.2"。
案例 2:0.1 + 0.2 ≠ 0.3(结果不精确)
同样先看 0.3 的二进制:
0.3₁₀ = 0.01001100110011...₂(还是 "0011" 无限循环)
转科学计数法:0.010011...₂ = 1.00110011...₂ × 2^(-2)
再看 0.1+0.2 的二进制相加过程:
0.1 的近似二进制(0.000110011...₂) + 0.2 的近似二进制(0.00110011...₂) = 0.0100110011...₂
这个相加结果,虽然数学上等于 0.3,但按 IEEE 754 存储时出了问题:
它的 "1.xxxx×2^e" 形式中,"xxxx" 部分的循环长度,在 52 位尾数位中 "无法完整容纳",舍入后的结果,和 "数学上 0.3 的二进制" 舍入后的存储值,差了一点点 ------ 简单说,这次相加的误差没有抵消,反而产生了新的误差,导致结果不等于 0.3 的存储值。
再用代码验证:
csharp
// 打印0.1+0.2的实际值
System.out.println(new BigDecimal(0.1).add(new BigDecimal(0.2)));
// 输出:0.3000000000000000444089209850062616169452667236328125
// 打印0.3的实际存储值
System.out.println(new BigDecimal(0.3));
// 输出:0.299999999999999988897769753748434595763683319091796875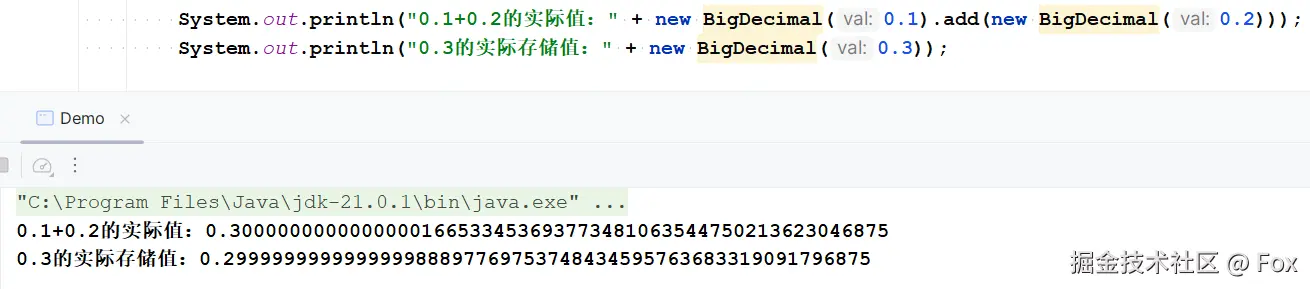
很明显,两个值不一样 ------ 所以计算机判定 "0.1+0.2≠0.3"。
三、面试标准答案模板:3 步说清,不慌不忙
遇到这道题,别只说 "二进制无法精确存储",要按 "原理→案例→总结" 的逻辑说,体现你的深度:
- 核心原因:IEEE 754 双精度存储的 "近似性"
计算机用 IEEE 754 双精度存储小数时,会先把十进制转二进制。但像 0.1、0.2、0.3 这类小数,二进制是无限循环的,而尾数位只有 52 位,必须舍入,所以存储的是 "近似值",不是数学上的精确值。加法结果是否相等,本质是 "两个近似值相加后,是否等于目标值的近似存储值"。
- 分案例拆解:为什么结果不同?
- 0.1+0.1=0.2:两个 0.1 的近似值相加后,得到的二进制值,刚好和 0.2 的近似存储值完全一致(舍入误差抵消),所以计算机判定相等;
- 0.1+0.2≠0.3:两个近似值相加后的二进制值,和 0.3 的近似存储值有微小差异(舍入误差叠加),所以判定不相等。可以用 BigDecimal 打印实际值来验证这个差异。
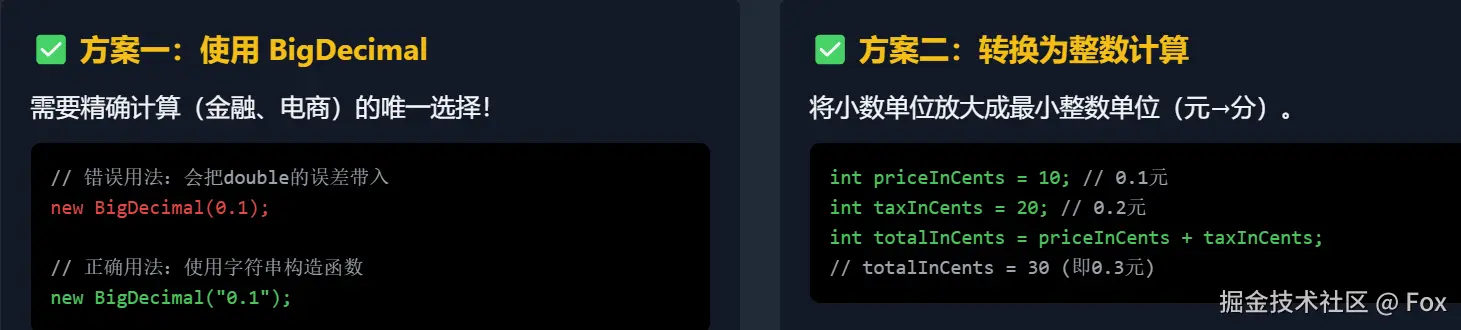
- 延伸总结:工程中怎么避免这个问题?
实际开发中,如果需要精确计算(比如金额),不能用 double/float,要改用:
- Java 用 BigDecimal(注意用 String 构造,别用 double 构造);
- 或者把小数转成整数计算(比如金额乘 100 转成分,计算完再转回来)。
其实这道题考的不是 "记结论",而是 "是否理解浮点数的存储本质"。只要把 "无限循环→尾数位舍入→近似值相加" 的逻辑说透,再结合代码验证,面试官就会觉得你不仅 "知其然",更 "知其所以然"。
你之前面试遇到过类似的 "反常识" 问题吗?评论区聊聊~
觉得有用的兄弟,点个赞,收藏起来,万一下次面试就用上了呢!
想了解更多高频面试题,欢迎关注公众号【Fox爱分享】,领取大厂高频面试真题。