项目开发中从补码到精度丢失的陷阱

背景

在最近的项目开发中，遇到了许多与二进制相关的问题，比如：

接口返回的 long 型数据精度丢失；
浮点数计算误差（如 0.1 + 0.2 ≠ 0.3）；
大整数运算或文件数据转化。

这些问题的本质，都离不开对 计算机底层二进制表示与运算规则 的理解。

基于此，这篇文章将讲解二进制的常见表示与运算法则，并结合项目中的实际案例，一步步剖析这些看似"神秘"的问题。

基础知识

计算机中的数据

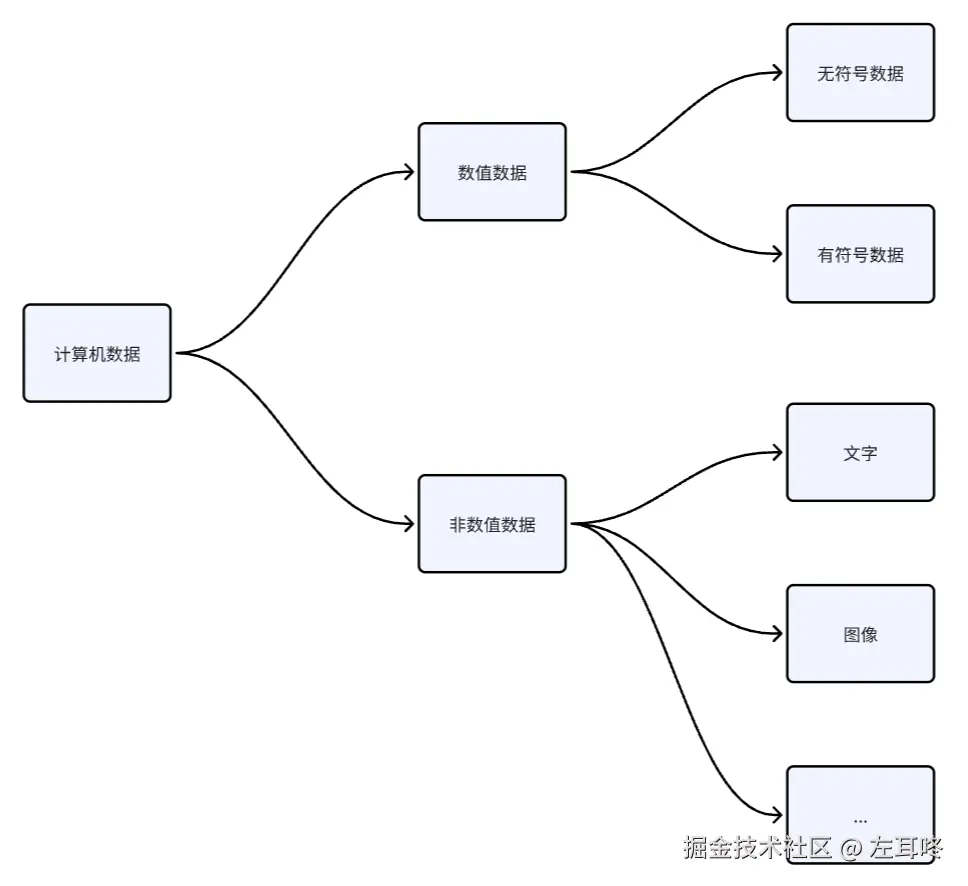
在计算机中，所有数据本质上都是由二进制（0 和 1）组成的。大体可以分为：

数值数据：无符号数据、有符号数据等；
非数值数据：字符、图像、音频等。

数值数据

无符号数据

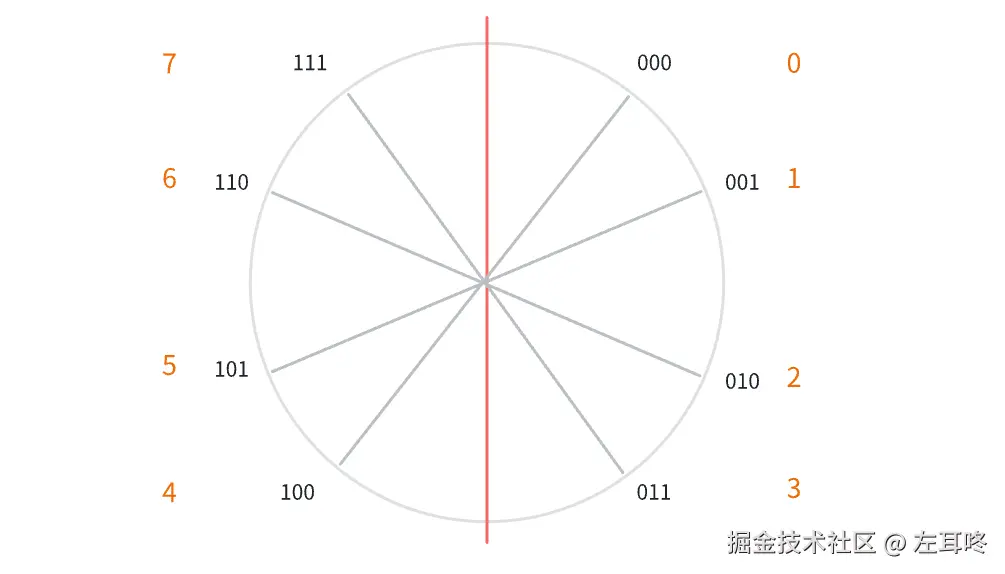
在二进制中，无符号数据通过 0、1 表示。

例如 3 个 bit 能表示 8 个数 (0、1、2、3、4、5、6、7)

有符号数据

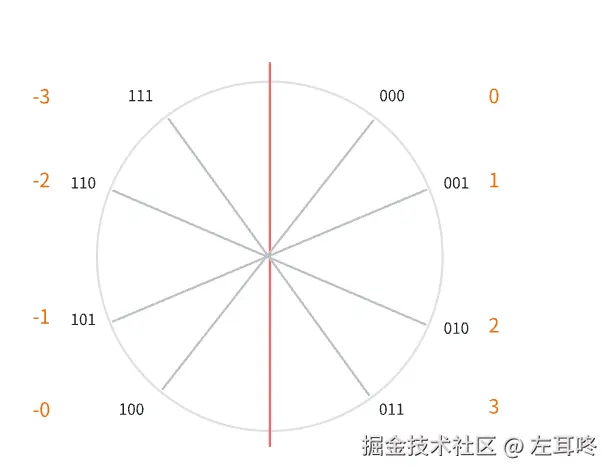
而有符号数据，则最高位通过 0、1表示正符号（0 是正数、1是负数）

例如 3 个 bit 能表示 8 个数 (+0、+1、+2、+3、-3、-2、-1、-0)

从反码到补码：计算机如何做减法

在二进制中，做加法非常简单，但"减法"其实是通过 加上补码 实现的。

例如 010 + 001 = 011 即 2 + 1 = 3，可当我需要做减法运算呢？

聪明的同学可能已经到了那就加上一个数的负数即可，例如 2 - 1 = 2 +（-1）= 1;

可当我们尝试进行运算时会发现 010 + 101 = 111（-3）显然答案是错误的。

那需要怎么做呢？

答案是在二进制中 减去一个数 等于 加上一个数的补码

在了解补码之前，我们需要先了解什么是反码

反码

反码指的是正数不变，负数除符号位取反

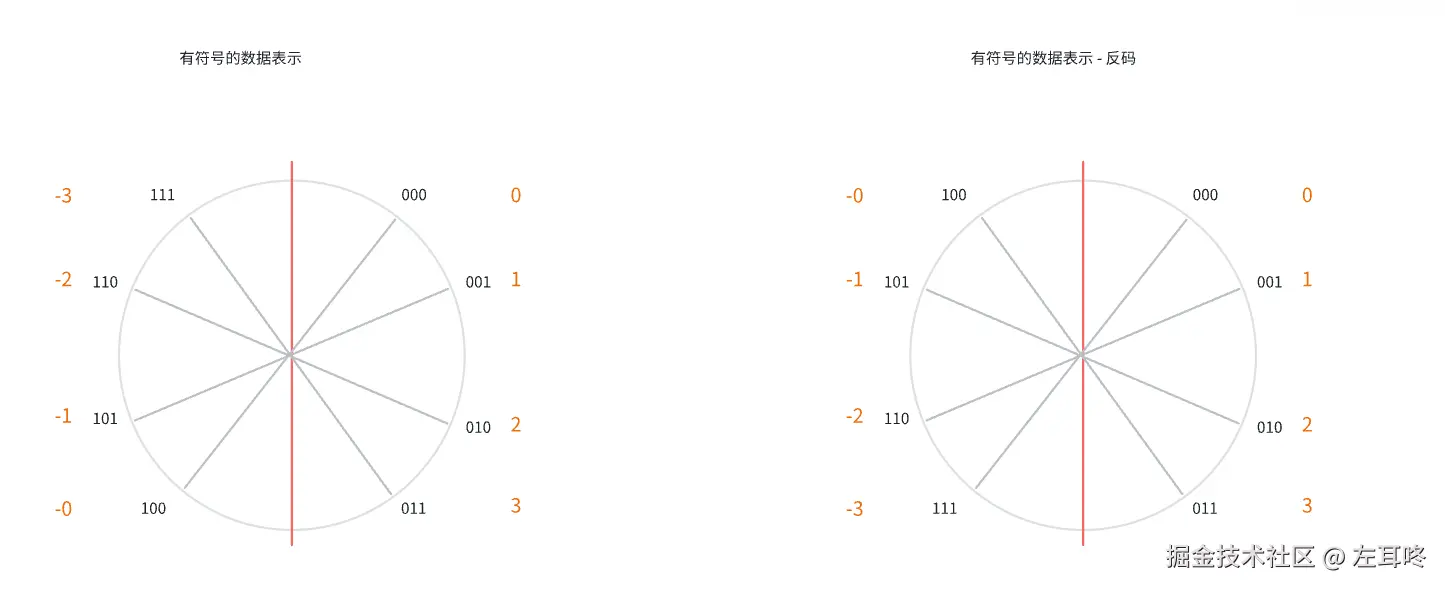
这时候有同学可能已经发现了规律，如下图所示

当正数的二进制每一位的取反后，就是他对应的负数，这就相当于在二进制中，减去一个数，相当于加上一个二进制数的反码。

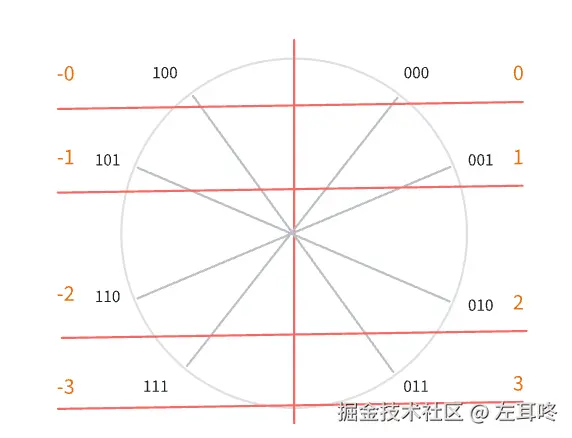
但反码中存在的缺点：0 存在着 2 种表示方法（+0、-0），但对于 0 来说，存在一种就可以了，没什么区别。

为了解决反码的缺点，补码就顺势而出了。

补码

正数不变，负数在反码的基础上加 1

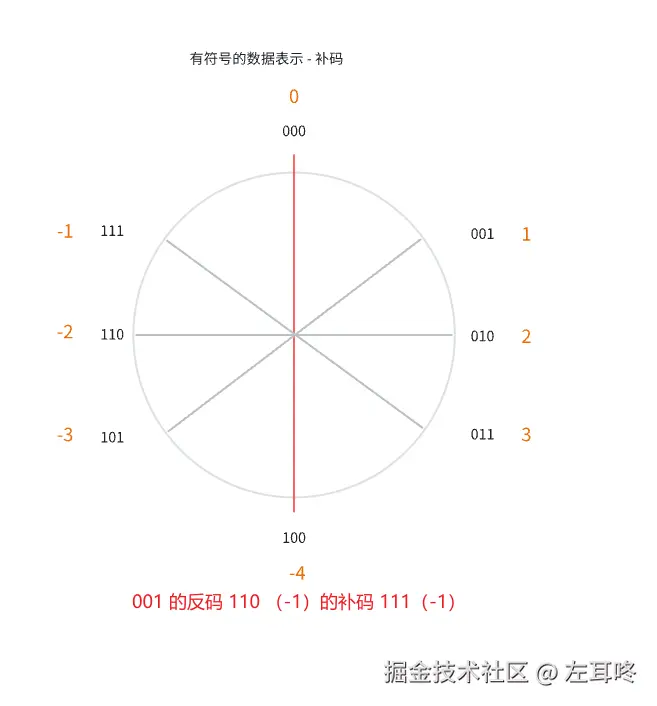
通过补码，在表示数量不变的基础上，解决了反码中存在 +0、-0 的冗余表示方法。

例如 010 - 001 => 010 + 111(补码) = 001

进制转化

二进制转十进制

以二进制 111.11 为例子

二进制转十进制的核心是 按位加权求和 ，即每个数位上的数字乘以 2 的对应幂次，然后将所有结果相加。整数部分和小数部分的计算规则略有不同，需分开处理。

1. 整数部分计算（111）

整数部分从右往左，幂次从 0 开始依次递增。

最右侧第 1 位（1）： <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 2 0 = 1 × 1 = 1 1 × 2⁰ = 1 × 1 = 1 </math>1×20=1×1=1
中间第 2 位（1）： <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 2 1 = 1 × 2 = 2 1 × 2¹ = 1 × 2 = 2 </math>1×21=1×2=2
最左侧第 3 位（1）： <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 2 2 = 1 × 4 = 4 1 × 2² = 1 × 4 = 4 </math>1×22=1×4=4
整数部分总和： <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 + 2 + 4 = 7 1 + 2 + 4 = 7 </math>1+2+4= 7

2. 小数部分计算（.11）

小数部分从左往右，幂次从 - 1 开始依次递减。

小数点后第 1 位（1）： <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 2 − 1 = 1 × 0.5 = 0.5 1 × 2⁻¹ = 1 × 0.5 = 0.5 </math>1×2−1=1×0.5=0.5
小数点后第 2 位（1）： <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 × 2 − 2 = 1 × 0.25 = 0.25 1 × 2⁻² = 1 × 0.25 = 0.25 </math>1×2−2=1×0.25=0.25
小数部分总和： <math xmlns="http://www.w3.org/1998/Math/MathML"> 0.5 + 0.25 = 0.75 0.5 + 0.25 = 0.75 </math>0.5+0.25= 0.75

3. 最终结果

将整数部分和小数部分相加，得到最终十进制结果：7 + 0.75 = 7.75

十进制转二进制

整数部分: 除 2 取余，直到商为 0。最先得到的余数是最低位，最后得到的余数是最高位。

小数部分: 乘 2 取整，直到积为 0 或者达到精度要求为止。最先得到的是整数最高位

例如十进制中的 7.75 可以转化为二进制的 111.11

整数部分是 111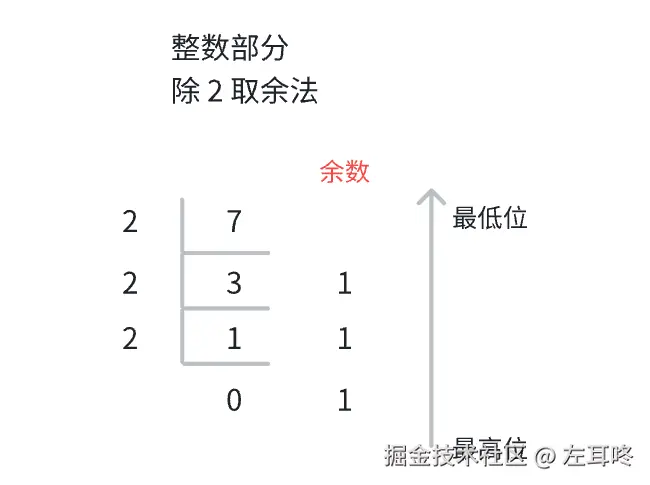

小数部分是 0.11 因此，十进制中的 7.75 是二进制中的 111.11

IEEE754 标准

JavaScript 采用 IEEE 754 双精度标准，用 64 位存储一个数字，结构分为三部分：

符号位（1 位） ：表示正负，0 为正，1 为负。
指数位（11 位） ：决定数值的数量级。
小数有效位（52 位） ：决定数值的精度，也称为 "尾数"。

在浮点数的科学计数法表示中

例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> 十进制中的 3.5 = 二进制中的 11.1 = 1.11 ∗ 2 1 十进制中的 3.5 = 二进制中的 11.1 = 1.11 * 2^1 </math>十进制中的3.5=二进制中的11.1=1.11∗21

最大精度

小数有效位是 "隐含了一位前导 1" 的。也就是说，52 位的小数有效位实际能表示 52+1=53 位二进制精度。

因此，它能精确表示的最大整数就是 2⁵³ - 1（因为 53 位二进制数的最大值是 "53 个 1"，即 2⁵³ - 1）。如果整数超过这个值，JavaScript 就无法保证精确存储和计算了。

实战案例

讲述完相对枯燥的基础知识后，接下来到了相对有趣的项目实战中遇到的案例进行分析。

案例 1：接口返回的 long 类型被 "改写"

某天, 前端小C和后端小Q 在对接接口的时候, 数据明明返回的是long类型 1981543253761712129, 可浏览器显示的却是 1981543253761712000

但这一切瞒不过刚学过 IEEE754 标准的小 C, 小 C 灵光一闪，因为 JavaScript 中最大整数是 2⁵³ - 1 （即 9007199254740991）

而输入的 1981543253761712129，该数字的二进制位数超过 53 位，尾数位（52 位 + 隐藏位 1 位）无法完整存储所有有效数字，JavaScript 会自动舍入，保留最接近的可表示值，导致末尾的 129 被舍去，使用偏移量补零为 000，最终结果为 1981543253761712000。

也可以在控制台输入 1981543253761712129 也会被丢弃转化为 1981543253761712000

案例 2：`0.1 + 0.2 !== 0.3`

0.1 通过 乘2取整法 转化为二进制过程中，存在着无限循环小数

而 0.2 也存在着无限循环小数

同理 0.3 也是存在着无限循环小数。

因此，在二进制中，0.1 + 0.2 != 0.3

解决方法也有特别多，常见的是通过 toFixed 方法进行精度截取。

案例 3：大整数加法（前端高精度计算）

在支付平台/钱包业务中，比较常见的就是大整数加法了, 常见的解法有双指针解法等等。。

js 复制代码

// 双指针解法
function lagerPhoneNumber(number1, number2) {
    // 确保number1是最小数
    if (number1.length > number2.length) {
      [number1, number2] = [number2, number1];
    }

    let res = "";
    const len1 = number1.length;
    const len2 = number2.length;
    let i = 0; // number1的指针
    let j = 0; // number2的指针
    let povit = 0; // 权重
    while (i < len1) {
      let num =
        Number(number1[len1 - 1 - i]) + Number(number2[len2 - 1 - j]) + povit;

      if (num >= 10) {
        povit = 1;
        num = num - 10;
      } else {
        povit = 0; // 重置
      }

      res = num + res;
      i++;
      j++;
    }

    // 最后考虑number2的情况
    while (j < len2) {
      let num = Number(number2[len2 - 1 - j]) + povit;

      if (num >= 10) {
        povit = 1;
        num = num - 10;
      } else {
        povit = 0; // 重置
      }

      res = num + res;
      j++;
    }

    if (povit) {
      // 最后一种情况
      res = 1 + res;
      povit = 0;
    }

    return res;
  }

最后

二进制、补码、IEEE754 这些概念看似"底层"，但在平时项目开发中影响巨大。

理解这些原理，能帮助我们在面对数据精度问题时，不再只是 "试出来"，而是 "看得懂、解释清、能修复"。