前言
同态加密其实是一种特殊的加密技术,它具有一种特殊的性质,即在密文上进行某种特定运算操作后,再解密得到的结果与在明文上进行同样的运算操作结果相同。换句话说,同态加密允许在加密状态下进行计算操作,而无需解密. 同态加密在加密货币领域具有极强重要的作用, 在多方协同签名进行转账, 智能合约方面都有同态加密的身影。
同态加密性质
同态加密,就是满足下面的性质的加密算法

- FHE支持无限次的乘法和加法运算,当前算法复杂度高,实际使用较少。
- SWHE支持有限次的加法和乘法运算。
- PHE只支持加法或乘法运算中的一种。
PHE在实际中使用的较多。 加法同态的算法有Paillier算法、DGK算法、OU算法、基于格密码的方案等。乘法同态有我们常见的RSA算法、ElGamal算法等。
前置知识
为了彻底理解同态加密,这里我列举了一些需要用到的数学定理,公式。
二次项定理/泰勒展开

唯一分解定理
每一个大于 1 的自然数 n n n,要么本身是质数(素数),要么可以唯一地写成一系列质数次方的乘积。
n = p 1 a 1 × p 2 a 2 × . . . × p n a n n=p_1^{a_1} \times p_2^{a_2} \times ... \times p_n^{a_n} n=p1a1×p2a2×...×pnan
其中 a 1 , a 2 . . . , a n a_1,a_2...,a_n a1,a2...,an均为正整数
剩余类/同余类
设模为 n n n,根据对 n n n取模将所有正整数分为 n n n类,记作 [ 1 ] , [ 2 ] , . . . [ n − 1 ] [1],[2],...[n−1] [1],[2],...[n−1], 记为 Z n Z_n Zn
a \] \[a\] \[a\] 表示 所有与整数 a a a模 n n n同余的整数构成的集合叫做模 n n n的一个剩余类, a a a为 \[ a \] \[a\] \[a\]的代表元 > 如 n = 5 , a = 1 , \[ 1 \] = 1 , 6 , 11 , 26 , 21... n=5,a=1,\[1\]=1,6,11,26,21... n=5,a=1,\[1\]=1,6,11,26,21...这些数字对5取模都为1 与 n 互质的剩余类,记为 Z n ∗ Z_n\^\* Zn∗ Z n ∗ = { a ∈ Z n ∣ g c d ( a , n ) = 1 } Z_n\^\*=\\{a\\in Z_n \| gcd(a,n)=1\\} Zn∗={a∈Zn∣gcd(a,n)=1} #### 费小马定理  #### 欧拉函数 ϕ ( n ) \\phi(n) ϕ(n)为小于等于 n n n的正整数中与 n n n互质的数的数 > 若 n n n为质数时很容易得到 ϕ ( n ) = n − 1 \\phi(n)=n−1 ϕ(n)=n−1 > > 如 p h i ( 5 ) phi(5) phi(5)=4,因为有4个数与5互质分别是:1,2,3,4 * 欧拉函数性质 : 若 p , q p,q p,q互质, n = p q , 则 ϕ ( n ) = ϕ ( p ) ϕ ( q ) = ( p − 1 ) ( q − 1 ) n=pq,则\\phi(n)=\\phi(p)\\phi(q)=(p−1)(q−1) n=pq,则ϕ(n)=ϕ(p)ϕ(q)=(p−1)(q−1) * 欧拉定理: 若 n n n与 a a a互质,则 a ϕ ( n ) ≡ 1 ( m o d n ) a\^{\\phi(n)} \\equiv 1 \\pmod n aϕ(n)≡1(modn) #### Carmichael 函数 对 n ∈ N , a ∈ N n \\in N, a \\in N n∈N,a∈N, 使 a m = 1 ( m o d n ) a\^m= 1 \\pmod n am=1(modn)恒成立的最小正整数 m m m, 记 λ ( n ) \\lambda(n) λ(n) * 对于素数 n n n, λ ( n ) = ϕ ( n ) = n − 1 \\lambda(n) = \\phi(n) = n-1 λ(n)=ϕ(n)=n−1(欧拉函数)。 * 但对于合数, λ ( n ) \\lambda(n) λ(n) 通常是 ϕ ( n ) \\phi(n) ϕ(n) 的真因数。 * 若 n = p k n = p\^k n=pk 是奇素数的幂, λ ( p k ) = ϕ ( p k ) = p k − 1 ( p − 1 ) \\lambda(p\^k) = \\phi(p\^k) = p\^{k-1}(p-1) λ(pk)=ϕ(pk)=pk−1(p−1) * 若 n = 2 k n = 2\^k n=2k, k ≥ 3 k \\geq 3 k≥3,则 λ ( 2 k ) = 2 k − 2 \\lambda(2\^k) = 2\^{k-2} λ(2k)=2k−2。 * 对于一般的合数 n = ∏ i = 1 m p i k i n = \\prod_{i=1}\^m p_i\^{k_i} n=∏i=1mpiki, λ ( n ) \\lambda(n) λ(n) 是所有 λ ( p i k i ) \\lambda(p_i\^{k_i}) λ(piki) 的最小公倍数。 ### Paillier算法 Paillier是一个支持**加法同态**的公钥密码系统,在众多PHE方案中,Paillier方案由于效率较高、安全性证明完备的特点,在各大顶会和实际应用中被广泛使用,是隐私计算场景中最常用的PHE实例化方案之一。 #### 密钥生成  #### 公钥加密 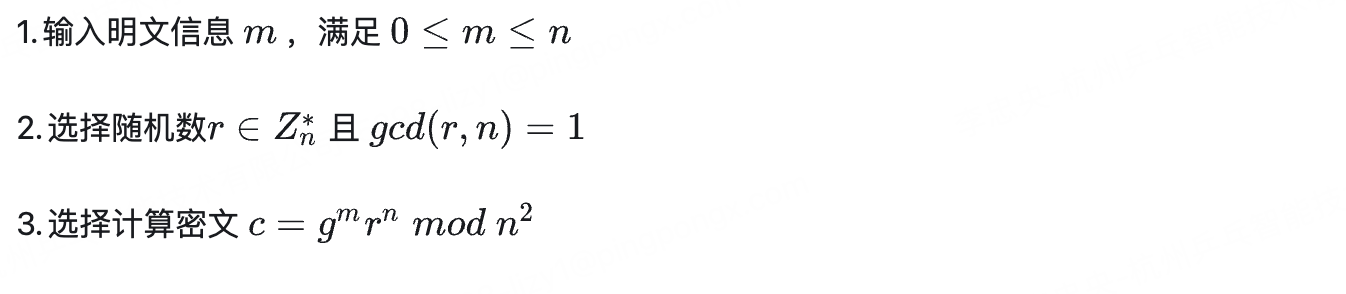 #### 私钥解密 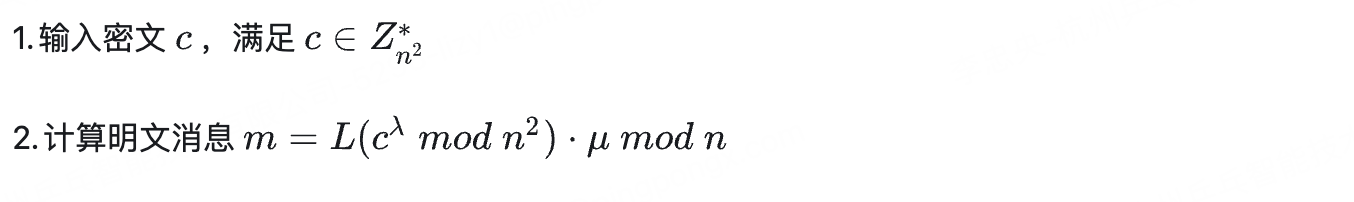 #### 证明   ### 总结 在环论中,同态加密本质是构造一个从明文环(如 Z n Z_n Zn )到密文环的环同态映射.加密函数 E : M → C E:M\\rightarrow C E:M→C 需满足 E ( m 1 + m 2 ) = E ( m 1 ) ⊕ E ( m 2 ) E ( m 1 ∗ m 2 ) = E ( m 1 ) ⊗ E ( m 2 ) E(m_1+m_2) =E(m_1) \\oplus E(m_2) \\\\E(m_1 \* m_2) =E(m_1) \\otimes E(m_2) E(m1+m2)=E(m1)⊕E(m2)E(m1∗m2)=E(m1)⊗E(m2) 其中 M M M 是明文空间(通常是一个环), C C C 是密文空间(另一个环或代数结构) ### 主要参考 《[费马小定理(通俗易懂)](https://zhuanlan.zhihu.com/p/616185983)》 《[应用密码学 \| Paillier同态加密算法简介](https://zhuanlan.zhihu.com/p/557034854)》 《[加密货币安全基石: 详解 Paillier 同态加密并使用币安tss-lib库](https://juejin.cn/post/7395377854602068031)》