freertos系统中如何生成随机数以及保证随机性？

文章目录

• 一、背景
• 二、伪随机算法
• • 2.1 线性同余生成器 (LCG)
  • 2.2 梅森旋转算法 (Mersenne Twister)
  • 2.3 平方取中法
  • 2.4 Xorshift
  • 2.5 密码学安全随机数
  • 2.6 算法选择考量
• 三、随机种子生成
• • 3.1 增加扰动熵源
  • 3.2 精确定时
  • 3.3 系统状态熵源混合
  • 3.4 随机种子生成熵源对比
• 四、CPU周期性计数器
• • 4.1 ARM&ARM64
  • • ARM (32-bit) 示例
    • ARM64 (AArch64) 示例
    • 重要实践提示:
  • 4.2 RISC-V架构
  • • 读取周期计数器的方法
    • 访问权限与配置
    • cycle与时间ms的转换
• 四、总结
• 五、参考资料

一、背景

freertos下如果使用加密、签名、SSL都需要用到随机数。linux下获取随机数很简单，C库已经提供了APIrand()，使用srand先设置好一个种子，通常使用系统时间，然后调用rand函数生成伪随机数序列。但是freertos没c库，所以需要自行实现random函数，核心是随机算法和随机种子，随机算法比较好实现，难点是随机种子的生成，freertos也没有time函数，如何生成一个具有随机的随机种子是本文着重探讨的。

#include <stdlib.h>
#include <stdio.h>
#include <time.h>
int main() {
   // 使用当前时间作为种子，确保每次运行生成不同的随机数
   srand((unsigned)time(NULL));
   // 生成并打印 10 个随机数
   for (int i = 0; i < 10; i++) {
       printf("Random Number: %d\n", rand());
   }
   return 0;
}

二、伪随机算法

软件实现的随机数生成，一般为伪随机数，根据算法计算得出一定随机的数据序列，由于算法固定，所以可能具有周期性重复的特性，且随机算法固定，如果知道种子值+随机算法，可以预测下一个随机数，所以需要种子值也有一定随机性。先介绍一下常见的随机数生成算法：

算法名称	主要原理	随机性周期	速度	安全性	典型应用场景
线性同余法(LCG)	使用线性公式 Xn+1=(aXn+c)modm递推	较短（≤m）	极快	低	简单模拟、游戏、对随机性要求不高的场景
梅森旋转算法(MT)	基于庞大的线性反馈移位寄存器状态数组	极长 (2^219937−1)	中等	低	科学计算、蒙特卡洛模拟、复杂系统仿真
Xorshift算法	通过连续的异或和移位操作快速改变内部状态	长（例如 232−1或更高）	极快	低	需要高速生成随机数的场景，如实时渲染、游戏
密码学安全算法	使用加密学哈希函数（如SHA-256）或加密算法（如AES）	依赖熵源质量	较慢	高	加密密钥生成、安全令牌、数字签名
真随机数生成器(TRNG)	基于物理现象（如热噪声、量子效应）	无限	可变	极高	高安全需求：密码学、安全协议、彩票抽奖

2.1 线性同余生成器 (LCG)

通过以下公式进行计算，原理是根据前一个随机数Xn乘一个系数a，在加上一个系数c，然后取余数。

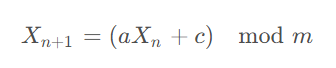
• 优点：

  速度快，算法简单

• 缺点：

  周期较短（最大周期为m），低位随机性差，通常取高位输出。

c语言代码实现：

#include <stdio.h>
#include <stdint.h>

typedef struct {
    uint32_t state;
    uint32_t a;
    uint32_t c;
    uint32_t m;
} LCG;

void lcg_init(LCG *lcg, uint32_t seed) {
    lcg->state = seed;
    lcg->a = 1103515245;
    lcg->c = 12345;
    lcg->m = 0x7FFFFFFF; // 2^31-1
}

uint32_t lcg_next(LCG *lcg) {
    lcg->state = (lcg->a * lcg->state + lcg->c) % lcg->m;
    return lcg->state;
}

int main() {
    LCG lcg;
    lcg_init(&lcg, 42);
    printf("LCG: %u\n", lcg_next(&lcg)); // 输出：1622650073
    return 0;
}

2.2 梅森旋转算法 (Mersenne Twister)

基于一个 624 维的状态数组，通过移位和异或操作生成随机数，Python random 模块的默认算法。

• 优点

周期极长（2^{19937}-1) ，且分布均匀。

• 缺点：

状态空间大，适合科学计算，但不适合加密。

c语言实现：

#include <stdio.h>
#include <stdint.h>

#define MT_N 624
#define MT_M 397

typedef struct {
    uint32_t state[MT_N];
    int index;
} MersenneTwister;

void mt_init(MersenneTwister *mt, uint32_t seed) {
    mt->state[0] = seed;
    for (int i = 1; i < MT_N; i++) {
        mt->state[i] = 0x6C078965 * (mt->state[i-1] ^ (mt->state[i-1] >> 30)) + i;
    }
    mt->index = MT_N;
}

void mt_twist(MersenneTwister *mt) {
    for (int i = 0; i < MT_N; i++) {
        uint32_t x = (mt->state[i] & 0x80000000) | (mt->state[(i+1)%MT_N] & 0x7FFFFFFF);
        x = (x >> 1) ^ ((x & 1) ? 0x9908B0DF : 0);
        mt->state[i] = mt->state[(i+MT_M)%MT_N] ^ x;
    }
    mt->index = 0;
}

uint32_t mt_next(MersenneTwister *mt) {
    if (mt->index >= MT_N) mt_twist(mt);
    uint32_t y = mt->state[mt->index++];
    y ^= (y >> 11);
    y ^= (y << 7) & 0x9D2C5680;
    y ^= (y << 15) & 0xEFC60000;
    y ^= (y >> 18);
    return y;
}

int main() {
    MersenneTwister mt;
    mt_init(&mt, 42);
    printf("Mersenne: %u\n", mt_next(&mt)); // 输出：1608637542
    return 0;
}

2.3 平方取中法

将当前数平方后取中间部分作为下一个数。例如，4位数 1234 平方为 1522756，取中间4位 5227。

• 优点：

算法简单。

• 缺点：

容易陷入短周期或退化到0。

C语言实现：

#include <stdio.h>
#include <stdint.h>

uint32_t middle_square(uint32_t seed, int digits) {
    uint64_t squared = (uint64_t)seed * (uint64_t)seed;
    uint32_t mask = 1;
    for (int i = 1; i < digits; i++) mask *= 10;
    squared /= mask; // 右移 digits/2 位
    squared %= (mask * 10); // 取中间 digits 位
    return (uint32_t)squared;
}

int main() {
    uint32_t seed = 1234;
    for (int i = 0; i < 5; i++) {
        seed = middle_square(seed, 4);
        printf("Middle Square: %u\n", seed); // 输出序列：5227, 3215, 3362...
    }
    return 0;
}

2.4 Xorshift

通过位运算（异或、移位）快速生成随机数。

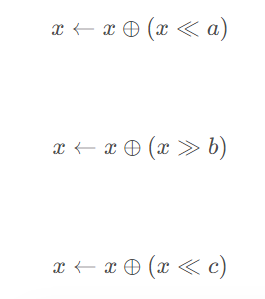
• 特点

速度快，周期长（232−12^{32}-1232−1或更高）。

c语言实现

#include <stdio.h>
#include <stdint.h>

typedef struct {
    uint32_t state;
} Xorshift32;

void xorshift32_init(Xorshift32 *xs, uint32_t seed) {
    xs->state = seed;
}

uint32_t xorshift32_next(Xorshift32 *xs) {
    xs->state ^= xs->state << 13;
    xs->state ^= xs->state >> 17;
    xs->state ^= xs->state << 5;
    return xs->state;
}

int main() {
    Xorshift32 xs;
    xorshift32_init(&xs, 42);
    printf("Xorshift: %u\n", xorshift32_next(&xs)); // 输出：2707161783
    return 0;
}

2.5 密码学安全随机数

上述随机数序列算法固定，如果知道种子和随机算法可以预测下一个随机数，对于密码学加密而言，可能会被破解，所以可以使用加密学哈希函数（如 SHA-256）或加密算法（如 AES、ChaCha20）生成不可预测的随机数。

2.6 算法选择考量

• 评估随机性需求 ：明确应用场景对随机数的统计特性 、不可预测性 和唯一性的要求。例如，科学模拟关注统计分布，而安全加密则强调不可预测性。
• 权衡性能与资源：在计算能力有限或对性能要求高的环境中，LCG和Xorshift是不错的选择。梅森旋转算法虽然提供高质量的随机数，但其状态空间较大。
• 理解算法的局限：例如，LCG生成的随机数低位随机性可能较差，而梅森旋转算法虽然统计性质优良，但不适用于加密场景。
• 种子质量的重要性：对于伪随机数生成器，种子的质量直接影响随机序列的起点。使用高熵源（如硬件噪声、系统时钟的精细读数）初始化种子，可以有效改善随机性。

简明选择策略：

• 通用应用，非安全场景 ：Python的random模块默认使用梅森旋转算法 ，C++标准库的std::mt19937也是可靠选择。
• 资源极度受限或极致性能要求 ：考虑Xorshift 或精心选择参数的LCG。
• 安全敏感应用（密码学） ：务必使用密码学安全的伪随机数生成器 ，如Java的SecureRandom，或操作系统提供的接口（如Linux的/dev/urandom）。
• 最高安全级别（如根密钥生成） ：使用真随机数生成器。

三、随机种子生成

linux下种子通常使用系统时间time，对应freertos下可以使用tick，但是freertos启动是严格按照时序执行的，而tick是ms级别的，每次启动执行代码初始化种子时tick值可能是一样的，所以需要需要增加熵源，可以从如下两个方面入手：

• 增加扰动
• 提高时间统计精度

3.1 增加扰动熵源

• 芯片内置的TRNG

芯片内置的TRING生成真随机数，但是一般MCU硬件可能不支持。

• ADC采样噪声

使用ADC模数转换，根据采样的噪声作为随机种子。

• 报文收发

通过报文收发交互，报文的随机时间来做为扰动。

3.2 精确定时

• tick

系统tick计时为ms级别，精度较低，对于一些场景可能不够。

• 高精度定时

使用cpu内部hrtimer高精度定时器进行定时。

• CPU周期计数器（cycle）

CPU中计算运行的周期数据，统计精度和主频对应的，精度很高。

3.3 系统状态熵源混合

混合一些任务调度状态、堆栈指针、中断时间戳等，但是堆栈指针有时因为freertos执行代码的严格时序性，堆栈内容也可能是一样。

3.4 随机种子生成熵源对比

方法分类	具体方法	实施关键	随机性质量	硬件依赖/成本	适用场景
硬件随机源	芯片内置真随机数发生器(TRNG)	调用厂商提供的SDK接口函数直接读取	高（真随机）	需要MCU硬件支持	加密、安全认证等对随机性要求极高的场景
	片内模拟模块的噪声（如ADC）	读取悬空或温度传感器ADC的低位噪声	较高	利用现有模拟外设，基本无额外成本	无TRNG，但对随机性有一定要求的场景
基于系统状态的熵源混合	结合多种运行时参数	混合系统tick计数 、中断时间戳 、高精度定时器、CPU周期计数器 、任务堆栈指针等的低位	中等（伪随机，但种子不可预测）	无额外硬件成本，依赖软件实现	通用应用，需要改善默认种子的场景
	报文收发	在一段网络报文交互后在计算系统时间。	中等	无	特定场景
外部熵源	使用独立的硬件随机数模块	通过SPI/I2C等总线读取外部器件数据	高（真随机）	需要额外硬件和连接	对随机质量有严苛要求且主控无TRNG的场景
非易失性存储维护种子	每次启动使用新种子并保存	将本次生成的优质随机数保存，作为下次启动的种子	中等（避免序列重复）	无额外硬件成本，需要非易失性存储器	希望每次上电随机序列都不同的场景

实施要点与选择建议：

• 硬件TRNG的利用：如果MCU支持硬件TRNG，这是最简单高效的方式。

• ADC噪声采集技巧：使用ADC采集噪声时，通常读取悬空引脚或内部温度传感器（需注意其电压波动范围）。通过连续多次采样并取这些采样值的低位进行组合（例如异或操作），可以提取到较好的随机熵源。

• 熵源混合的代码示例：下面是一个混合多种系统状态生成种子的C代码示例：

  // 生成随机种子
  unsigned int generate_random_seed(void) {
  unsigned int seed = 0;
  // 获取系统tick计数
  seed ^= (xTaskGetTickCount() & 0xFFFF);
  // 获取某个全局变量或函数指针的地址（具有一定随机性）
  seed ^= ((uint32_t)(&seed) >> 2) & 0xFFFF;
  // 可以添加其他熵源，如ADC读取的噪声低位等
  return seed;
  }

  // 在程序初始化阶段调用
  void main_task(void *pvParameters) {
  unsigned int seed = generate_random_seed();
  srand(seed); // 初始化标准库随机种子
  // ... 其他初始化代码
  }

• 非易失性存储种子的注意事项：采用此方法时，需要确保在写入新种子前系统已获得了高质量的随机数，以避免将可预测或有缺陷的随机序列延续到下一次启动。

四、CPU周期性计数器

CPU周期性计数器(cycle)精度是和CPU主频一样，比如CPU主频1G，那么cycle的单位是1ns，是比较好的随机源。下面介绍一下不同架构下cycle的获取。

4.1 ARM&ARM64

arm架构可以通过如下方式获取高精度时间戳：

特性对比	ARM (32-bit, e.g., ARMv7/A/R)	ARM64 (AArch64)
首选计数器	PMU 周期计数器 (PMCCNTR)	PMU 周期计数器 (PMCCNTR_EL0)
访问指令	MRC p15, 0, <Rt>, c9, c13, 0	MRS <Xt>, PMCCNTR_EL0
计数器特性	直接统计 CPU 时钟周期数，精度最高。	直接统计 CPU 时钟周期数，精度最高。
访问要求	通常需要在特权模式（如内核态）下访问。	可在用户态访问，但通常需要内核先使能 PMUSERENR_EL0寄存器。
备选方案	通用定时器 (CNTVCT)，但其频率固定，可能与 CPU 频率不同。	通用定时器 (CNTVCT_EL0)，系统级计数器，频率固定（ARMv8.6+ 通常为 1GHz），不受 CPU 调频影响。

ARM (32-bit) 示例

使用 PMU 周期计数器 (PMCCNTR) 的示例代码如下。请注意，访问 PMU 寄存器通常需要在内核态或具有相应权限的环境下进行。

/* 使能 PMU 和周期计数器 */
static inline void enable_pmu(void) {
    uint32_t value;

    // 启用 PMU 全局控制 (设置 PMCR.E 位)
    asm volatile("MRC p15, 0, %0, c9, c12, 0" : "=r"(value));
    value |= 1; // 设置 E 位
    asm volatile("MCR p15, 0, %0, c9, c12, 0" :: "r"(value));

    // 启用周期计数器 (设置 PMCNTENSET.C 位)
    value = (1 << 31); // C 位对应 bit 31
    asm volatile("MCR p15, 0, %0, c9, c12, 1" :: "r"(value));
}

/* 读取周期计数器 */
static inline uint32_t read_pmu_cycle_counter(void) {
    uint32_t value;
    asm volatile("MRC p15, 0, %0, c9, c13, 0" : "=r"(value));
    return value;
}

// 使用示例
enable_pmu();
uint32_t start_cycle = read_pmu_cycle_counter();
// ... 要测量的代码段 ...
uint32_t end_cycle = read_pmu_cycle_counter();
uint32_t cycles_elapsed = end_cycle - start_cycle;

ARM64 (AArch64) 示例

在 ARM64 下，使用 PMCCNTR_EL0寄存器可以获取最高精度的 CPU 周期。以下是在用户态读取的示例，前提是内核已启用用户态访问。

/* 直接读取 PMU 周期计数器 (需要内核使能用户态访问) */
static inline uint64_t read_pmu_cycle_counter_el0(void) {
    uint64_t value;
    asm volatile("mrs %0, PMCCNTR_EL0" : "=r"(value));
    return value;
}

/* 读取通用定时器 CNTVCT_EL0 (通常总可在用户态读取) */
static inline uint64_t read_cntvct_el0(void) {
    uint64_t value;
    asm volatile("mrs %0, cntvct_el0" : "=r"(value));
    return value;
}

/* 读取通用定时器的频率 */
static inline uint64_t read_cntfrq_el0(void) {
    uint64_t freq;
    asm volatile("mrs %0, cntfrq_el0" : "=r"(freq));
    return freq;
}

// 使用示例：测量代码段消耗的CPU周期
uint64_t start = read_pmu_cycle_counter_el0();
// ... 要测量的代码段 ...
uint64_t end = read_pmu_cycle_counter_el0();
uint64_t cpu_cycles = end - start;

// 使用示例：使用通用定时器测量实际时间
uint64_t freq = read_cntfrq_el0(); // 获取定时器频率 (Hz)
uint64_t start_time = read_cntvct_el0();
// ... 要测量的代码段 ...
uint64_t end_time = read_cntvct_el0();
double time_elapsed_seconds = (double)(end_time - start_time) / freq;

重要实践提示:

1. 访问权限与内核使能 ：在 ARM64 上，虽然 CNTVCT_EL0通常可在用户态直接读取，但为了在用户态读取 PMCCNTR_EL0，通常需要内核模块或驱动程序的配合，以设置 PMUSERENR_EL0等寄存器来启用用户态访问。直接尝试在用户态执行相关指令可能会触发非法指令异常。
2. 多核一致性：与 x86 的 TSC 类似，在多核 ARM 系统上，不同 CPU 核心的周期计数器（特别是 PMU 计数器）在启动时可能不是同步的。如果测量涉及线程在核心间迁移，可能会影响结果。对于精确测量，最好将线程绑定到单个 CPU 核心。
3. 功耗管理的影响 ：现代处理器的动态调频（DVFS）技术可能会影响基于 CPU 周期的 PMU 计数器的递增速率。而通用定时器（如 CNTVCT_EL0）基于一个独立的、通常频率固定的系统计数器，因此其计数值更稳定，适合测量真实的"挂钟时间"。
4. 计数器溢出 ：PMU 周期计数器在 ARM32 下是 32 位，在长时间测量时需注意溢出问题。ARM64 下的 PMCCNTR_EL0是 64 位，溢出周期极长，在大多数场景下可忽略。

根据你的具体需求来选择合适的方法：

• 追求最高精度，测量纯 CPU 工作量 ：优先使用 PMU 周期计数器 (PMCCNTR/PMCCNTR_EL0)，它能最真实地反映代码执行的 CPU 周期成本。
• 测量真实（挂钟）时间，或无法控制 CPU 频率 ：使用通用定时器 (CNTVCT/CNTVCT_EL0)，其结果更接近实际流逝的时间。
• 考虑便捷性和通用性 ：CNTVCT_EL0在 ARM64 用户态下的可访问性通常更好，是一个简单可靠的选择。

4.2 RISC-V架构

在RISC-V架构中，高精度的时间统计通常通过读取其内置的周期计数器（cycle计数器）来实现，下表介绍RISC-V中与时间测量相关的三个基本计数器及其用途。

计数器名称	访问指令/伪指令	主要用途说明
周期计数器 (CYCLE)	RDCYCLE/ RDCYCLEH(RV32)	统计处理器核心执行的时钟周期数 ，适用于测量CPU密集型任务的执行效率。
实时时钟计数器 (TIME)	RDTIME/ RDTIMEH(RV32)	统计实际经过的挂钟时间，更贴近实际耗时，但其递增速率通常由平台特定的时钟源决定。
退休指令计数器 (INSTRET)	RDINSTRET/ RDINSTRETH(RV32)	统计硬件线程退休的指令数量，可用于计算CPI(Clock Per Instruction)等指标。

读取周期计数器的方法

直接使用RISC-V架构定义的伪指令是读取周期计数器最便捷和可移植的方式。

1. 使用伪指令 ：在汇编代码中，你可以直接使用 RDCYCLE这条伪指令。编译器会将其转换为相应的 csrr(Control and Status Register Read) 指令来读取底层的 cycle寄存器。

   unsigned long long get_cycle_count(void) {
       unsigned long long cycles;
       // 对于RV64架构，一条指令即可读取完整的64位计数器
       __asm__ volatile ("rdcycle %0" : "=r"(cycles));
       // 对于RV32架构，内联汇编的实现见后续说明
       return cycles;
   }

2. RV32架构下的安全读取：由于RV32的寄存器是32位宽，而周期计数器是64位的，需要分两次读取（先低32位，后高32位）。为了保证在两次读取之间计数器低32位溢出时高32位不会出错，需要使用一个循环来确保读取值的正确性。下面的代码序列演示了如何安全地读取：

   unsigned long long get_cycle_count_rv32(void) {
       unsigned int hi, lo, hi2;
       do {
           __asm__ volatile (
               "rdcycleh %0\n"  // 读取高32位到hi
               "rdcycle  %1\n"  // 读取低32位到lo
               "rdcycleh %2"    // 再次读取高32位到hi2
               : "=r"(hi), "=r"(lo), "=r"(hi2)
           );
       } while (hi != hi2); // 比较两次读取的高位，如果不相等则说明发生了溢出，需要重试
       return ((unsigned long long)hi << 32) | lo;
   }

访问权限与配置

在使用周期计数器前，需要注意其访问权限和配置。

• 特权级别 ：cycle计数器属于 Zicntr扩展的一部分，通常可以在非特权模式（如用户模式）下直接读取。这为你直接在应用程序代码中插入性能测量点提供了便利。
• 计数器使能：虽然架构定义了计数器，但具体的RISC-V芯片实现可能需要通过机器模式（M-mode）的控制状态寄存器（CSR）来启用这些计数器。你需要查阅你所使用芯片的数据手册或编程手册，确认是否需要以及如何配置。

cycle与时间ms的转换

可以使用cycle做精确的时间计算，cycle计时的计算公式：

时间(秒) = 周期数 / CPU主频

四、总结

freertos\vxworks\ucos等实时操作系统没有提供随机数生成的，伪随机算法有很多可以直接使用，重点在于随机种子的生成，关键在于扰动+精度，建议使用cpu周期计数器+常见扰动（adc采样+报文交互）。本文详细介绍了随机算法和随机种子生成，以及尤其介绍了CPU周期计数器这种常见计时和随机种子的使用方法，希望对你有帮助。

五、参考资料

https://blog.csdn.net/qq_62784677/article/details/147240398