CSP集训错题集 第八周 主题：基础图论

apcipot_rain2025-11-04 9:25

E

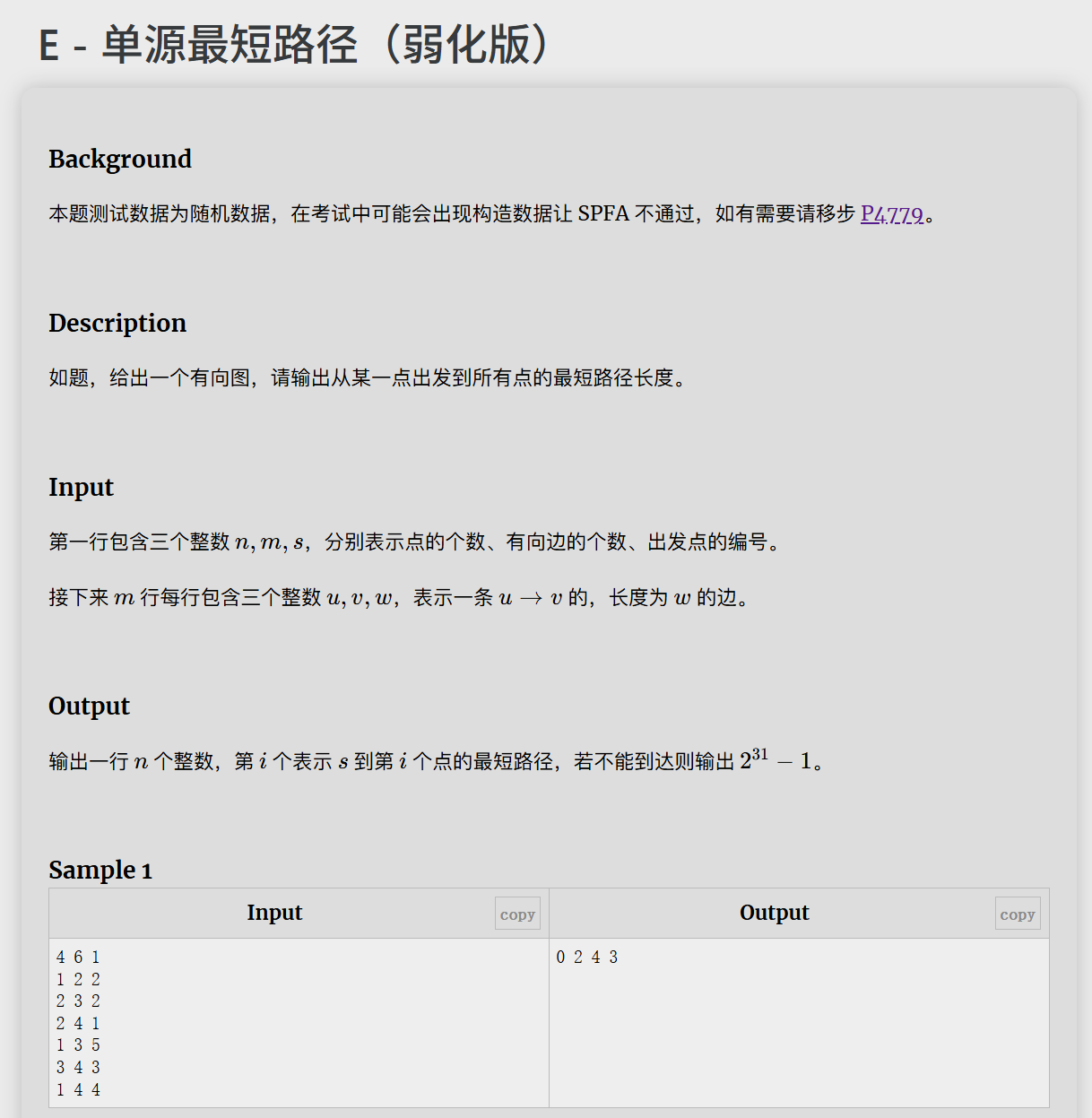
单源最短路径，让我捡回迪杰斯特拉。。。

上一把写迪杰斯特拉还是实验课：数据结构实验------基于 Dijsktra 算法的最短路径求解_编程题实训-实验5-基于dijsktra-CSDN博客。

我就不再提上面的s山了，现在我的写法优化了很多。这个算法的核心就两步：

1.比较di[lst].res+w和di[nxt].res，如果更小代表解更优，就更新。

更新不仅是di[nxt].res，而且di[nxt].pre也需要更新成lst。

2.比较di[i].res，寻找最小值，作为下一个点。

然后就是其它的建结构体、初始化等内容。

最后注意，可能有非连通的情况，比如这个点：

输入：

5 15 5

2 2 270

1 4 89

2 1 3

5 5 261

5 2 163

5 5 275

4 5 108

4 4 231

3 4 213

3 3 119

3 1 77

3 1 6

2 4 83

5 5 196

5 5 94

输出

166 163 2147483647 246 0

所以，while终止的条件不应该是集齐所有点cnt==n，而是lst==-1，也就是下一个点不存在。

Code

cpp 复制代码 
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
struct node{
	bool vis;
	int res,pre;
}di[100005];
int n,m,s,u,v,w;
vector<vector<pair<int,int> > > a(100005);
void init();
void dijkstra();
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m>>s;
	init();
	for(int i=1;i<=m;i++){
		cin>>u>>v>>w;
		a[u].push_back({v,w}); 
	}
	dijkstra();
	for(int i=1;i<=n;i++){
		cout<<di[i].res<<' ';
	}
	cout<<endl;
	return 0;
}
void init(){
	for(int i=1;i<=n;i++){
		di[i].vis=0;
		di[i].res=2147483647;
		di[i].pre=i;
	}
}
void dijkstra(){
	int cnt=0;//如果cnt=n那么遍历完，终止 
	di[s].res=0;//起始位置res等于0 
	
	int lst=s;//lst表示上一个的位置 
	//while(cnt<n)写法是错的 
	while(lst!=-1){//可能不是连通图 
		//标记lst已经被遍历过了 
		di[lst].vis=1;
		
		//lst上一个 nxt下一个 wei权值 
		for(int i=0;i<a[lst].size();i++){
			int nxt=a[lst][i].first;
			int wei=a[lst][i].second;
			
			if(di[lst].res+wei<di[nxt].res){
				di[nxt].res=di[lst].res+wei;
				di[nxt].pre=lst;
			}
		}
		
		int minres=2147483647,minpos=-1;
		for(int i=1;i<=n;i++){
			if(i==s) continue;
			if(di[i].vis==1) continue;
			//没有被遍历而且距离最短 
			if(di[i].res<minres){
				minpos=i;
				minres=di[i].res;
			}
		}
		lst=minpos;//下一个遍历的位置就是minpos的位置 
		//cout<<lst<<endl;//用来测试下一个点位 
		
		cnt++;
	} 
}

F

同样的题面，数据变大了。

关于一些疑问，D老师还是很权威的：

以这个为例：

4 6 1

1 2 2

2 3 2

2 4 1

1 3 5

3 4 3

1 4 4

理论输出：0 2 4 3

首先(0,1)入队，然后得到(2,2) (4,4) (5,3)，都会入队。

但是(4,4) (5,3)显然不是最优解，

那么请问这是怎么过滤掉的？

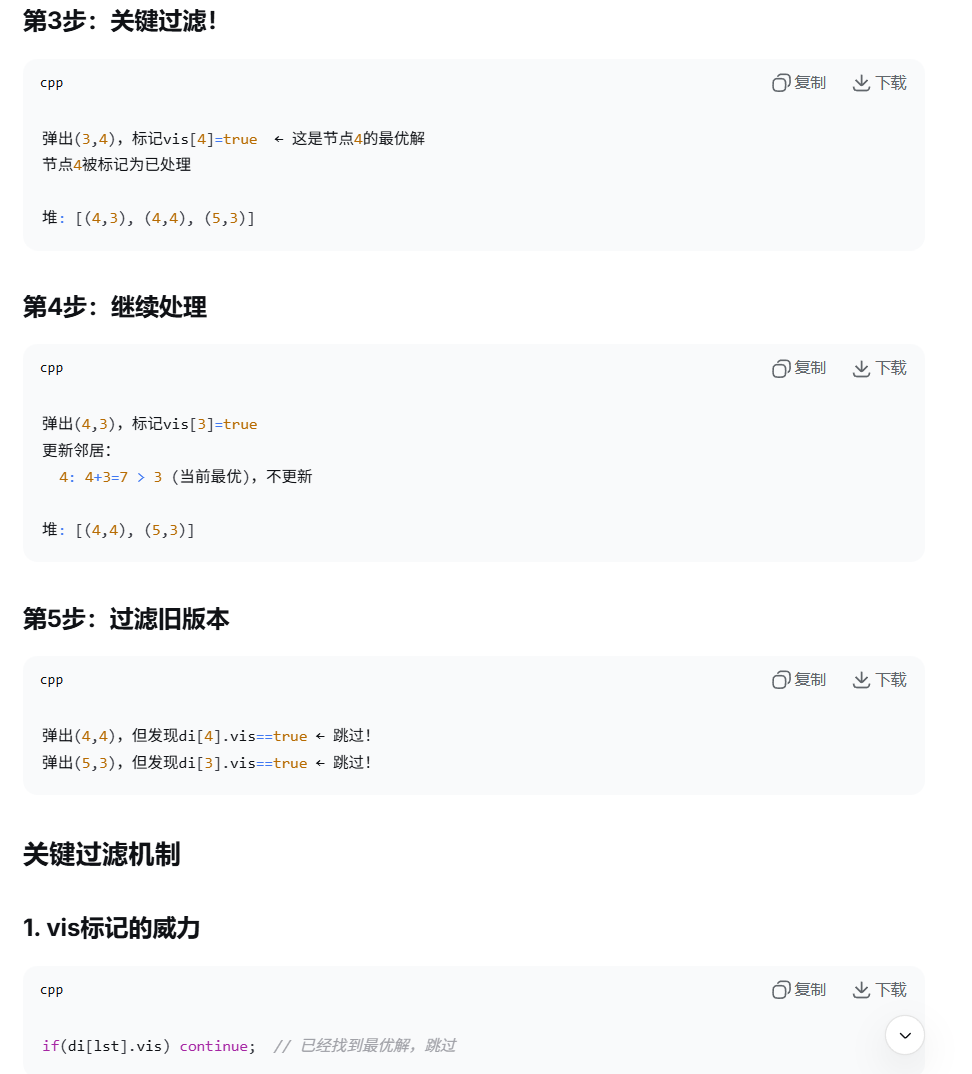
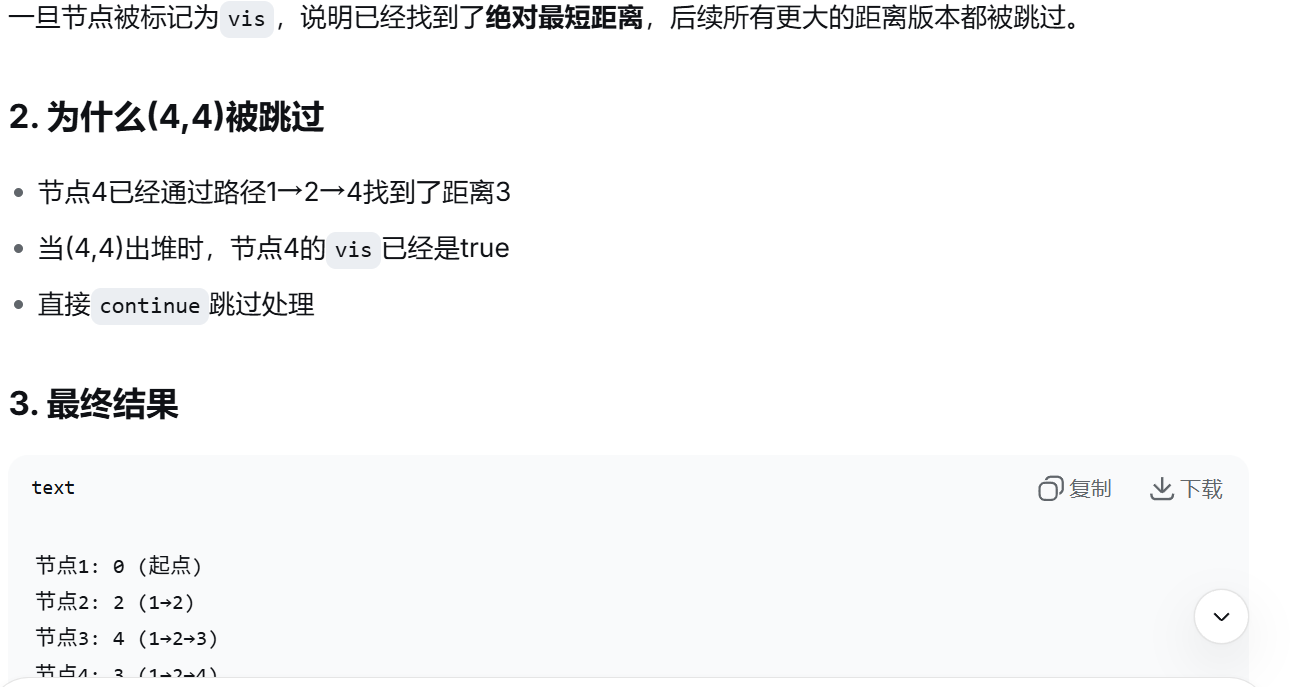
有一些过程解不是最优解，会因为小根堆的排序而排到后面去。

然后因为vis标记，所以你从队列首部取出来的必定是最优解，等到你做完一圈最优解之后，尽管还有一些糟粕解留在队列里，但是因为vis=1被跳过。（比如第五步，这题里的[4,4][5,3]）。

Code

cpp 复制代码 
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
struct node{
	bool vis;
	int res,pre;
}di[100005];
int n,m,s,u,v,w;
vector<vector<pair<int,int> > > a(100005);
priority_queue<
	pair<int,int>,
	vector<pair<int,int> >,
	greater<pair<int,int> >
	//存储的数据类型，底层容器，比较函数（小顶堆，最小元素在堆顶，先一后二） 
> pq;
void init();
void dijkstra();
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m>>s;
	init();
	for(int i=1;i<=m;i++){
		cin>>u>>v>>w;
		a[u].push_back({v,w}); 
	}
	dijkstra();
	for(int i=1;i<=n;i++){
		cout<<di[i].res<<' ';
	}
	cout<<endl;
	return 0;
}
void init(){
	for(int i=1;i<=n;i++){
		di[i].vis=0;
		di[i].res=2147483647;
		di[i].pre=i;
	}
}
void dijkstra(){
	di[s].res=0;//起始位置res等于0 
	pq.push({0,s});//距离、节点  

	while(!pq.empty()){
		int lst=pq.top().second;//上一个元素 
		pq.pop();//一定要及时出队！ 
		
		if(di[lst].vis)
			continue;
		di[lst].vis=1;
		
		//lst上一个 nxt下一个 wei权值 
		for(int i=0;i<a[lst].size();i++){
			int nxt=a[lst][i].first;
			int wei=a[lst][i].second;
			
			if(di[lst].res+wei<di[nxt].res){
				di[nxt].res=di[lst].res+wei;
				di[nxt].pre=lst;
				pq.push({di[nxt].res,nxt});
			}
		}
	} 
}

G

变种dijkstra

有向图->无向图。"You are given a simple connected undirected graph......"

只有边权重->点也有权重。

其实想通了也很简单，把点权重和边权重加一起就行了。然后起始距离不是0而是第一个点权重。

cpp 复制代码 
    for(i64 i=1;i<=m;i++){
   		cin>>u>>v>>w;
		a[u].push_back({v,w}); 
		a[v].push_back({u,w});
	}


	di[s].res=b[s];//起始位置res等于0 
	pq.push({b[s],s});//距离、节点  


            if(di[lst].res+wei+b[nxt]<di[nxt].res){
				di[nxt].res=di[lst].res+wei+b[nxt];
				di[nxt].pre=lst;
				pq.push({di[nxt].res,nxt});
			}

H

这一题我比较明确是什么意思，但是想不到有什么高效解法，又去问了D老师。

原来可以把这张图看成树，先定一个节点（我定1），然后计算所有点距离根节点的距离。

然后又给出了一个公式：

距离 = depth[c] + depth[d] - 2 × depth[lca(c,d)]

距离%2==1 输出Road；距离%2==0 输出Town。

lca是什么？

实际上和lca无关，因为 2 × depth[lca(c,d)]%2==0 ，不影响结果。本来想学的，但是看着很抽象，什么"向上跳2^k步"，劝退，劝退。

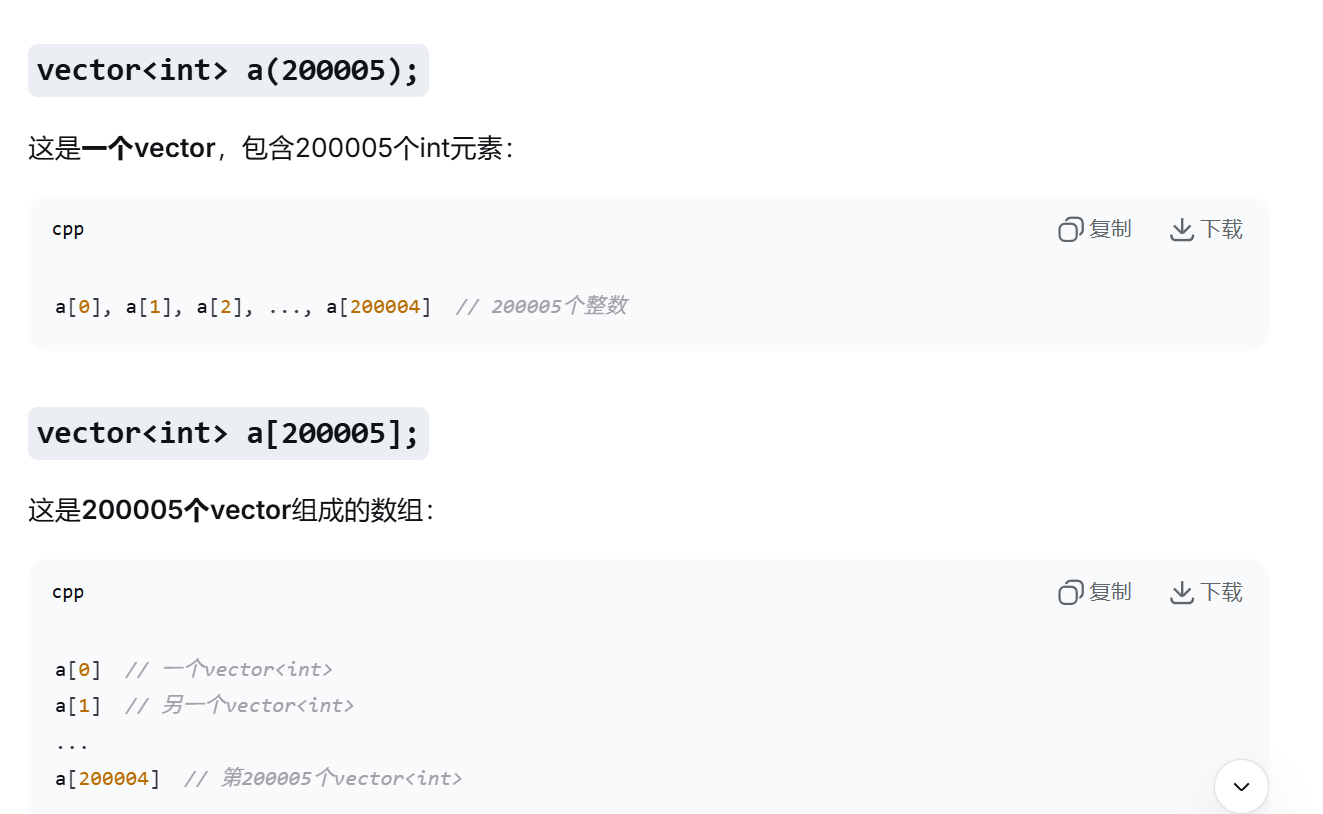
写到这里，我发现我有点搞不清

vector<int> a[200005];

vector<vector<pair<int,int> > > a(100005);

这两玩意

cpp 复制代码 
#include<iostream>
#include<vector>
#include<queue>
#define i64 long long
using namespace std;
i64 n,q,u,v;
vector<i64> a[200005];
i64 dis[200005];
void bfs();
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>q;
	for(i64 i=1;i<=n-1;i++){
		cin>>u>>v;
		a[u].push_back(v);
		a[v].push_back(u);
	}
	bfs();
	while(q--){
		cin>>u>>v;
		i64 ans=dis[u]+dis[v];
		if(ans%2==1) cout<<"Road"<<endl;
		else if(ans%2==0) cout<<"Town"<<endl;
	}
	return 0;
}
void bfs()
{
	bool s[200005];
	queue<i64> q;
	q.push(1);
	s[1]=1;
	i64 depth=0;
	while(!q.empty()){
		q.push(0);
		++depth;
		while(q.front()!=0)
		{
			i64 lst=q.front();
			q.pop();
			for(i64 i=0;i<a[lst].size();i++){
				i64 nxt=a[lst][i];
				if(s[nxt])
					continue;
				s[nxt]=1;
				dis[nxt]=depth;
				q.push(nxt);
			}
		}
		q.pop();
	}
}

I

bfs记层可解，但是对32错7。

然后我发现，居然是一个代码冗余带来的灾难？？?

如果三个节点，但是只有两条边，是(1,2)(2,1)，仍成立。

纪律性这一块

cpp 复制代码 
#include<iostream>
#include<vector>
#include<queue>
#define i64 long long
using namespace std;
i64 n,m,u,v;
vector<i64> a[200005];
void bfs();
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(i64 i=1;i<=m;i++){
		cin>>u>>v;
		a[u].push_back(v);
	}
	/*if(n>m){
		cout<<-1<<endl;
		return 0;
	}*///错误代码 
	bfs();
	return 0;
}
void bfs()
{
	bool s[200005]={0},flag=0;
	i64 depth=0;
	queue<i64> q;
	//s[1]=1;怀疑这点是不需要的 
	q.push(1);
	while(!q.empty()&&!flag){
		++depth;
		q.push(0);
		while(q.front()!=0&&!flag){
			i64 lst=q.front();
			q.pop();
			for(int i=0;i<a[lst].size();i++){
				int nxt=a[lst][i];
				if(s[nxt])
					continue;
				
				if(nxt==1)//找到目标1 
					flag=1;
					
				s[nxt]=1;
				q.push(nxt);
			}
		}
		q.pop();
	}
	while(!q.empty()){//队列全部放空，享受素质人生 
		q.pop();
	}
	if(flag) cout<<depth<<endl;
	else cout<<-1<<endl; 
	return ;
}

J

并查集的思路

但是、对于每个连通分量，点数和边数如何统计？

我们可能想到，有那么多个点，但是只有几个连通分量，所以很难统计。可是实际上，往往都是空间换时间的过程，我们就开两个数组去存储边数和点数，就会方便很多。（这种思路很妙而且对于我这种初学者有点反直觉）

那么每两个点进来，就不仅是联合操作一次，而且边和点都要操作，实际上就是相加就可以了sz[x]+=sz[y]; edge[x]+=edge[y]+1;

这题一开始WA了两次，是因为 edge[x]++ 错写成 edge[x]=y ，edge[x]+edge[y]+1 错写成 edge[x]=edge[y]+1。

cpp 复制代码 
#include<iostream>
#define i64 long long
using namespace std;
i64 n,m,u,v,ans=0;
i64 pre[200005]={0},sz[200005]={0},edge[200005]={0};
void init();
void unite();
i64 find(i64 num);
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	init();
	for(i64 i=1;i<=m;i++){
		cin>>u>>v;
		unite();
	}
	for(i64 i=1;i<=n;i++){
		if(pre[i]==i){//自己 
			ans+=sz[i]*(sz[i]-1)/2-edge[i]; 
		}
	}
	cout<<ans<<endl; 
	return 0;
}
void init(){
	for(int i=1;i<=n;i++){
		pre[i]=i;
		sz[i]=1;//特别 
	}
}
void unite(){
	i64 x=find(v),y=find(u);
	if(x==y){
		edge[x]=y;//如果两个点祖宗一致，那么单纯的边增加，不会带来点的问题。 
		return ;
	}
	//如果祖宗不一样，那么说明两个图之间变连通，原来两个点的点、边数据现在合并到一个点y上 
	pre[y]=x;//y依靠于x，那么x是核心 
	sz[x]+=sz[y]; 
	edge[x]=edge[y]+1;	
	return ;
}
i64 find(i64 num)
{
	if(pre[num]==num) return num;
	else return pre[num]=find(pre[num]);
}

K

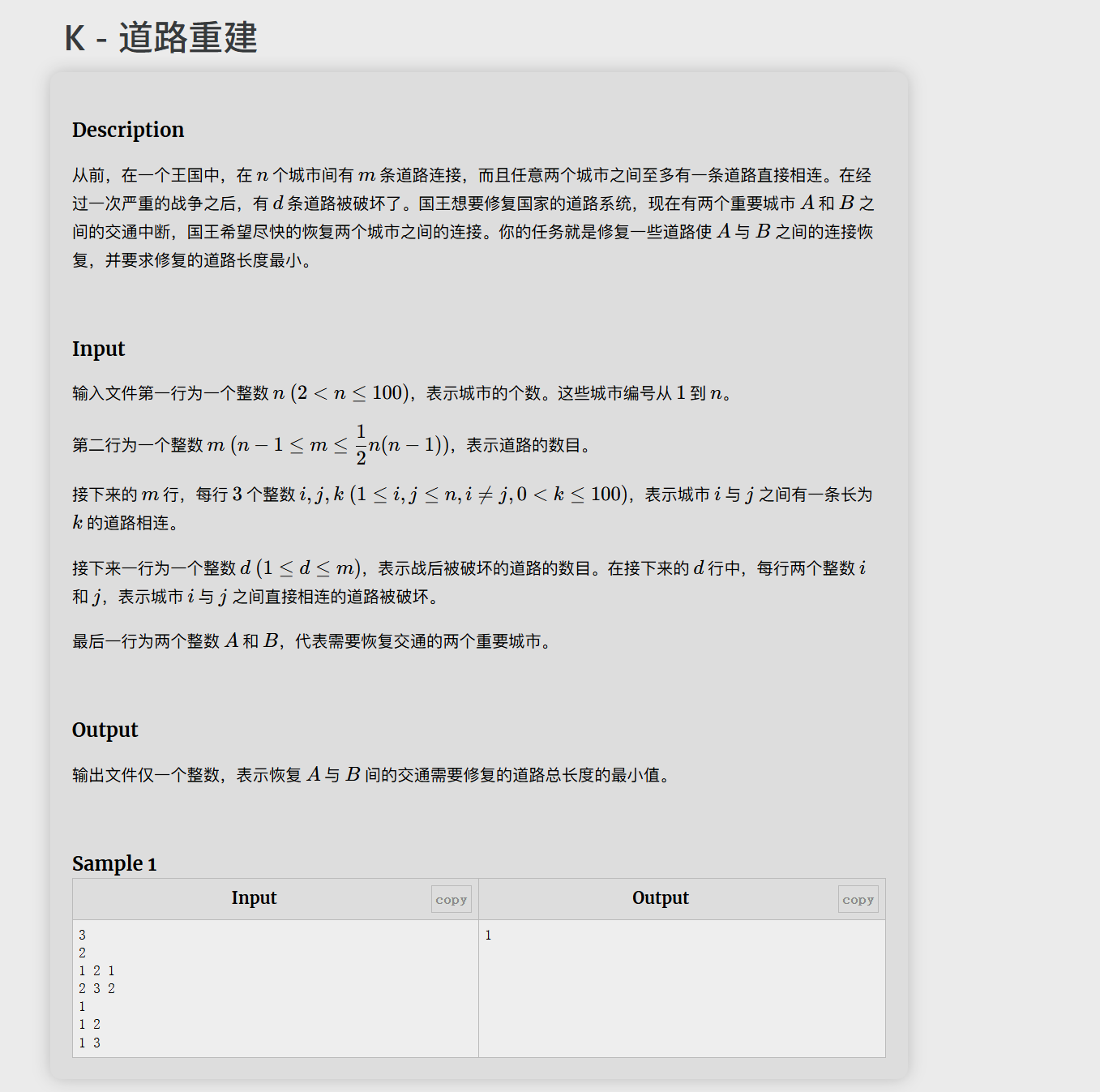
n<=100，那么懒得vector了，直接上邻接矩阵。

学到现在，算法无非就是dfs bfs 并查集 dijkstra，而现在分析题面的能力越来越重要了。

分析这题：灾后重建，有的桥带权，但是没有被破坏，所以实际上这个权不应该被计算进去。

如果把这个权置为0，那么是不是也是一个最短路径dijkstra？

所以我们借用一个数组操作一下，让没有被破坏的边权值变0，有破坏的边权值正常显示，其它都是MX。那么这题就结束了。

cpp 复制代码 
#include<iostream>
#include<queue>
#define MX 10086
#define i64 long long
using namespace std;
struct node{
	bool vis;
	int res,pre;
}di[105];
priority_queue<
	pair<int,int>,
	vector<pair<int,int> >,
	greater<pair<int,int> >
> pq;
i64 n,m,t,u,v,w,st=0,ed=0,ans=0;
i64 a[105][105]={0};
bool broken[105][105]={0};
void init();
void dijkstra();
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	init();
	cin>>st>>ed;
	dijkstra();
	return 0;
}
void dijkstra(){
	di[st].res=0;
	pq.push({0,st});
	while(!pq.empty()){
		i64 lst=pq.top().second;
		pq.pop();
		
		if(di[lst].vis)
			continue;
		di[lst].vis=1;
			
		for(i64 i=1;i<=n;i++){
			if(a[lst][i]==MX)
				continue;
			
			i64 wei=a[lst][i];
			i64 nxt=i;
			
			if(di[lst].res+wei<di[nxt].res){
				di[nxt].res=di[lst].res+wei;
				di[nxt].pre=lst;
				pq.push({di[nxt].res,nxt});
			}
		}
	}
	/*for(int i=1;i<=n;i++)
		cout<<di[i].res<<endl;*/
	cout<<di[ed].res<<endl;
	return ;
}
void init(){
	cin>>n>>m;
	//初始化全部是MX 
	for(i64 i=1;i<=n;i++){
		di[i].res=MX;
		for(i64 j=1;j<=n;j++){
			a[i][j]=MX;
		}
	}
	//开始输入路径 
	for(i64 i=1;i<=m;i++){
		cin>>u>>v>>w;
		a[u][v]=w;
		a[v][u]=w;
	}
	//标记谁被破坏了 
	cin>>t;
	for(i64 i=1;i<=t;i++){
		cin>>u>>v;
		broken[u][v]=1;
		broken[v][u]=1;
	}
	//如果原来有路，而且没被破坏，道路置0 
	for(i64 i=1;i<=n;i++){
		for(i64 j=1;j<=n;j++){
			if(a[i][j]!=MX&&!broken[i][j]){
				a[i][j]=0;
			}
		}
	}
	//输出演示 
	/*for(i64 i=1;i<=n;i++){
		for(i64 j=1;j<=n;j++){
			cout<<a[i][j]<<' ';
		}
		cout<<endl;
	}*/
	return ;
}

M

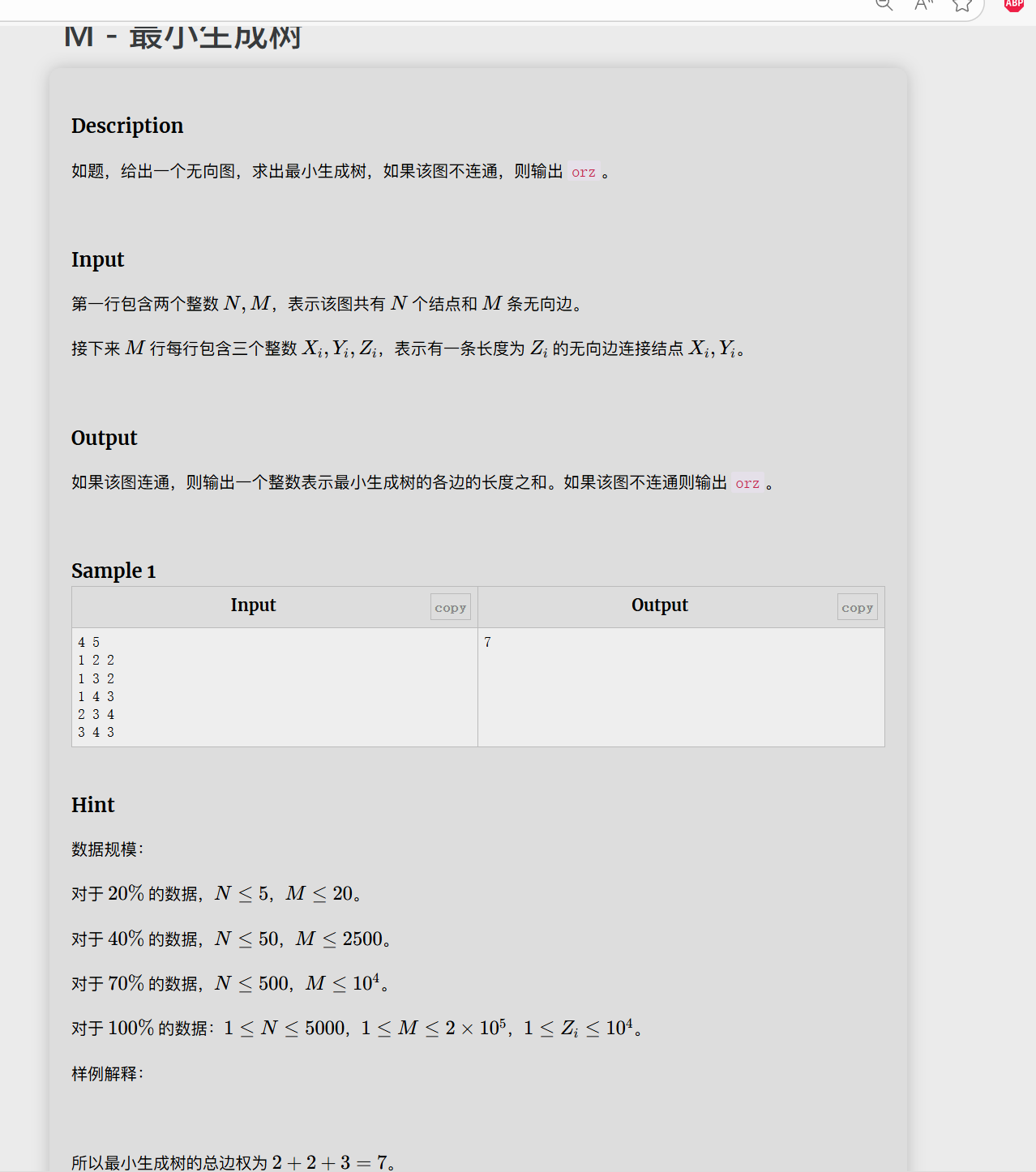
学了数据结构或者离散数学的都能知道Prim和Kruskal（避圈法）算法。算法很好理解，但是避圈法太难实现，所以我用prim。

我找的题解在这：最小生成树算法 - 洛谷专栏

其实不用完整看这个题解，你看一遍Prim的演示图你就知道这算法是个啥意思了。和迪杰斯特拉不能说一模一样但是确实是很像。内核都是bfs更新。不过最短路径着重点是点，最小生成树着重点是边。所以造成了判定条件略微的不一样。

然后这题依旧是稳定发挥交上去无法AC，因为一开始感觉a[5005][5005]还行，懒得用vector，但是MLE了4个点，所以只好换vector了。

cpp 复制代码 
#include<iostream>
#include<queue>
#define MX 10086
#define i64 long long
using namespace std;
i64 n,m,u,v,w,res=0;
i64 dis[5005]={0};
vector<pair<i64,i64> > a[5005];
bool s[5005]={0};
priority_queue<//来个堆更方便排序 
	pair<i64,i64>,
	vector<pair<i64,i64> >,
	greater<pair<i64,i64> >
> q;
void init();
void prim();
bool check();
int main(){
	cin>>n>>m;
	init();
	for(i64 i=1;i<=m;i++){
		cin>>u>>v>>w;
		a[u].push_back({v,w});//可能存在重边 
		a[v].push_back({u,w});
	}
	prim();
	if(check()) cout<<res<<endl; 
	else cout<<"orz"<<endl;
	return 0;
}
void init(){
	for(i64 i=1;i<=n;i++){
		dis[i]=MX;
	}
	return ;
}
void prim(){
	//把1作为根节点 
	dis[1]=0;
	q.push({0,1});//路径在前节点在后，堆根据这样排序 
	while(!q.empty()){
		i64 lst=q.top().second;//取出队首，能被取出来的一定是贪心最优解 
		i64 distance=q.top().first;
		q.pop();
		
		if(s[lst]==1)//如果被遍历过 
			continue;
		s[lst]=1; 
		
		for(i64 i=0;i<a[lst].size();i++){
			i64 nxt=a[lst][i].first;
			i64 wei=a[lst][i].second;
			if(s[nxt]) continue;
			if(wei>=dis[nxt]) continue;
			
			dis[nxt]=wei;
			q.push({wei,nxt});
		}
	}
	return ;
}
bool check(){
	for(i64 i=1;i<=n;i++){
		if(dis[i]==MX){
			return 0;
		}
		res+=dis[i];
	}
	return 1;
}

N

我一开始以为，这又是一个复杂的一批的题目，打开洛谷，啊？橙题？啊？题解代码这么短？

首先看这题可能被这个路径给吓到了，但是实际上我们并不关注中间还要经过多少额外节点，这题直接就是一个M个点之间的最短路径求和问题，不就行了？

所以这个纯纯就是纸老虎。我们只需要求出每个点对每个点的最短路径就行了。而Floyd算法复杂度为O(n3)，100的数据恰到好处不会TLE。那么a不断更新就可以了。

不过，身为菜鸟级选手，为啥floyd这么写捏？

中间这一行是个dp更新最小值，很好理解，难的就是怎么理解k在i和j的前面。

这个文章描述的很好，D老师描述的我倒是没怎么理解到。

https://blog.csdn.net/qq_43753724/article/details/129507989

cpp 复制代码 
#include<iostream>
#define MX 10086
#define i64 long long
using namespace std;
i64 a[105][105]={0}, b[10005]={0};
i64 n,m,ans=0;
void floyd();
int main(){
	cin>>n>>m;
	for(i64 i=1;i<=m;i++){
		cin>>b[i];
	}
	for(i64 i=1;i<=n;i++){
		for(i64 j=1;j<=n;j++){
			cin>>a[i][j];
		}
	}
	floyd();
	for(i64 i=2;i<=m;i++){
		ans+=a[b[i-1]][b[i]];
	}
	cout<<ans;
	return 0;
}
void floyd(){
	for(i64 k=1;k<=n;k++){
		for(i64 i=1;i<=n;i++){
			for(i64 j=1;j<=n;j++){
				a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
			}
		}
	}
	return ;
}
相关推荐
sheeta199810 小时前
LeetCode 每日一题笔记 日期：2025.11.24 题目：1018. 可被5整除的二进制前缀
笔记·算法·leetcode
gfdhy16 小时前
【c++】哈希算法深度解析：实现、核心作用与工业级应用
c语言·开发语言·c++·算法·密码学·哈希算法·哈希
百***060116 小时前
SpringMVC 请求参数接收
前端·javascript·算法
一个不知名程序员www17 小时前
算法学习入门---vector（C++）
c++·算法
云飞云共享云桌面17 小时前
无需配置传统电脑——智能装备工厂10个SolidWorks共享一台工作站
运维·服务器·前端·网络·算法·电脑
福尔摩斯张17 小时前
《C 语言指针从入门到精通：全面笔记 + 实战习题深度解析》(超详细)
linux·运维·服务器·c语言·开发语言·c++·算法
橘颂TA17 小时前
【剑斩OFFER】算法的暴力美学——两整数之和
算法·leetcode·职场和发展
xxxxxxllllllshi18 小时前
【LeetCode Hot100----14-贪心算法(01-05),包含多种方法，详细思路与代码，让你一篇文章看懂所有！】
java·数据结构·算法·leetcode·贪心算法
前端小L18 小时前
图论专题(二十二)：并查集的“逻辑审判”——判断「等式方程的可满足性」
算法·矩阵·深度优先·图论·宽度优先
铁手飞鹰18 小时前
二叉树（C语言，手撕）
c语言·数据结构·算法·二叉树·深度优先·广度优先
热门推荐
01GitHub 镜像站点02【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连03BongoCat - 跨平台键盘猫动画工具04UV安装并设置国内源05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Google Antigravity：无法登录？早期错误、登录修复和用户反馈指南07Linux下V2Ray安装配置指南08全球最强模型Grok4，国内已可免费使用！（附教程）09Spring Boot 4.0 发布总结：新特性、依赖变更与升级指南10Labelme从安装到标注：零基础完整指南