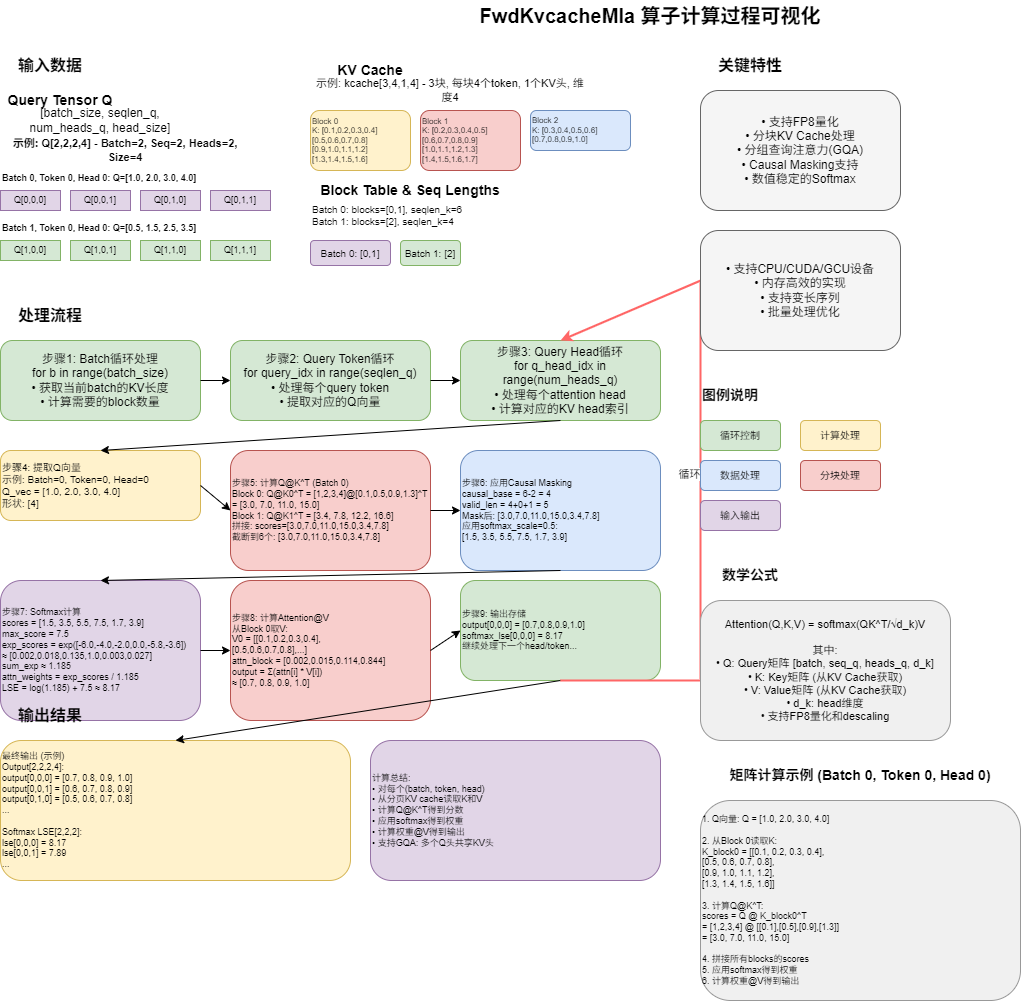
FwdKvcacheMla 算子详细数据流程讲解
📋 目录
1. 算子整体架构
核心公式
Attention(Q, K, V) = softmax(Q @ K^T * scale) @ V整体数据流
输入层 计算层 输出层
┌─────────┐ ┌──────────┐ ┌─────────┐
│ Q │────────>│ │ │ output │
│ [B,S,H,D]│ │ │───────────>│[B,S,H,D]│
├─────────┤ │ │ ├─────────┤
│ KCache │────────>│ Attention│ │softmax_ │
│[N,P,K,D]│ │ Compute │───────────>│ lse │
├─────────┤ │ │ │[B,H,S] │
│seqlens_k│────────>│ │ └─────────┘
│ [B] │ │ │
├─────────┤ │ │
│block_ │────────>│ │
│ table │ └──────────┘
│ [B,M] │
└─────────┘
B=batch_size, S=seqlen_q, H=num_heads_q
N=num_blocks, P=page_block_size, K=num_heads_kv
D=head_size, M=max_blocks_per_seq2. 输入数据详解
2.1 Query张量 (q)
形状 : [batch_size, seqlen_q, num_heads_q, head_size]
具体示例 : [2, 2, 4, 64]
含义解释:
- batch_size=2: 同时处理2个请求
- seqlen_q=2: 每个请求当前要生成2个token
- num_heads_q=4: 每个token有4个注意力头
- head_size=64: 每个头的向量维度是64
物理含义:
q[0, 0, 0, :] 表示:
- 第0个请求(batch 0)
- 第0个要生成的token(query token 0)
- 第0个注意力头(head 0)
- 的查询向量(64维)数据示例 (简化为4维):
python
# batch=0, token=0, head=0
q[0,0,0] = [1.0, 2.0, 3.0, 4.0, ...(共64个数)]
└─┬─┘ └─┬─┘ └─┬─┘ └─┬─┘
维度0 维度1 维度2 维度3
# 这个向量用来和历史的Key向量做点积,找出相关的历史信息2.2 KV Cache张量 (kcache)
形状 : [num_blocks, page_block_size, num_heads_kv, head_size]
具体示例 : [8, 16, 2, 64]
含义解释:
- num_blocks=8: 总共有8个内存块
- page_block_size=16: 每个块存储16个token的K和V
- num_heads_kv=2: KV有2个头(GQA: 4个Q头共享2个KV头)
- head_size=64: 每个头的向量维度是64
分块存储结构:
Block 0: [token_0, token_1, ..., token_15] (16个token)
Block 1: [token_16, token_17, ..., token_31]
Block 2: [token_32, token_33, ..., token_47]
...
为什么分块?
- 支持动态序列长度
- 避免大块连续内存
- 方便不同请求共享cache数据示例:
python
# Block 0, token 0, kv_head 0 的Key向量
kcache[0, 0, 0, :] = [0.1, 0.2, 0.3, 0.4, ...(共64个数)]
# Block 0存储的所有Key向量:
kcache[0, :, 0, :] =
[[0.1, 0.2, ..., 0.64], # token 0
[0.2, 0.3, ..., 0.65], # token 1
...
[1.5, 1.6, ..., 2.13]] # token 15
形状: [16, 64]2.3 序列长度 (seqlens_k)
形状 : [batch_size]
具体示例 : [32, 48]
含义:
- batch 0 有32个历史token
- batch 1 有48个历史token
物理含义:
每个请求的上下文长度不同:
- 请求0可能是: "今天天气"(已生成4个token) + 28个历史token
- 请求1可能是: "人工智能的发展"(已生成7个token) + 41个历史token2.4 块映射表 (block_table)
形状 : [batch_size, max_num_blocks_per_seq]
具体示例 : [2, 4]
python
block_table = [
[0, 1, -1, -1], # batch 0使用block 0和1,后面是padding
[2, 3, 4, -1] # batch 1使用block 2、3、4
]
含义:
告诉算子每个batch的历史token存储在哪些block中
查找过程:
如果要找 batch 0 的第20个历史token:
1. 20 // 16 = 1 (在第1个block)
2. block_table[0, 1] = 1 (对应物理block 1)
3. 20 % 16 = 4 (block内的第4个位置)
4. 因此: kcache[1, 4, kv_head, :]2.5 其他参数
python
softmax_scale = 1.0 / sqrt(head_size) # 通常是 1/sqrt(64) = 0.125
is_causal = True # 是否使用因果mask(生成任务需要)
head_size_v = 64 # Value的维度3. 完整计算流程
流程图总览
开始
│
├──> for batch in [0, 1]: ────────────────┐
│ │
│ 获取当前batch的KV长度 seqlens_k[batch] │
│ 计算需要的block数量 │
│ │
│ ├──> for query_token in [0, 1]: ────┤
│ │ │
│ │ ├──> for q_head in [0,1,2,3]: ──┤
│ │ │ │
│ │ │ ┌──────────────────────────┼──────────┐
│ │ │ │ 步骤A: 提取Q向量 │ │
│ │ │ │ q_vec = q[b,t,h] │ │
│ │ │ │ 形状: [64] │ │
│ │ │ └──────────┬───────────────┘ │
│ │ │ │ │
│ │ │ ┌──────────▼───────────────┐ │
│ │ │ │ 步骤B: 计算Q@K^T │ │
│ │ │ │ for block in blocks: │ │
│ │ │ │ k = kcache[block] │ │
│ │ │ │ scores = q_vec @ k.T │ │
│ │ │ │ 拼接所有scores │ │
│ │ │ │ 形状: [kv_len] │ │
│ │ │ └──────────┬───────────────┘ │
│ │ │ │ │
│ │ │ ┌──────────▼───────────────┐ │
│ │ │ │ 步骤C: Causal Mask │ │
│ │ │ │ 设置未来位置为-inf │ │
│ │ │ │ 形状: [kv_len] │ │
│ │ │ └──────────┬───────────────┘ │
│ │ │ │ │
│ │ │ ┌──────────▼───────────────┐ │
│ │ │ │ 步骤D: Apply Scale │ │
│ │ │ │ scores *= softmax_scale │ │
│ │ │ │ 形状: [kv_len] │ │
│ │ │ └──────────┬───────────────┘ │
│ │ │ │ │
│ │ │ ┌──────────▼───────────────┐ │
│ │ │ │ 步骤E: Softmax │ │
│ │ │ │ max_s = max(scores) │ │
│ │ │ │ exp_s = exp(scores-max_s)│ │
│ │ │ │ weights = exp_s/sum(exp_s)│ │
│ │ │ │ lse = log(sum)+max_s │ │
│ │ │ │ 形状: [kv_len] │ │
│ │ │ └──────────┬───────────────┘ │
│ │ │ │ │
│ │ │ ┌──────────▼───────────────┐ │
│ │ │ │ 步骤F: Attention@V │ │
│ │ │ │ for block in blocks: │ │
│ │ │ │ v = kcache[block] │ │
│ │ │ │ out += weights @ v │ │
│ │ │ │ 形状: [64] │ │
│ │ │ └──────────┬───────────────┘ │
│ │ │ │ │
│ │ │ ┌──────────▼───────────────┐ │
│ │ │ │ 步骤G: 存储结果 │ │
│ │ │ │ output[b,t,h] = out │ │
│ │ │ │ softmax_lse[b,h,t] = lse │ │
│ │ │ └──────────────────────────┘ │
│ │ │ │
│ │ └──> 下一个head ─────────────────────────┘
│ │ │
│ └──> 下一个query_token ─────────────────────┘
│ │
└──> 下一个batch ─────────────────────────────────┘
│
结束4. 数据维度变化追踪
完整的一次计算 (batch=0, query_token=0, q_head=0)
步骤 操作 输入形状 输出形状 数值示例
─────────────────────────────────────────────────────────────────────────────
0. 初始化 - - - -
1. 提取Q向量 q[0,0,0,:] [2,2,4,64] [64] [1.0, 2.0, 3.0, ...]
↓
[1.0, 2.0, 3.0, 4.0, ..., 64个数]
2. 获取KV信息 seqlens_k[0] [2] 标量: 32 32
block_table[0] [2,4] [2] [0, 1]
blk_num = ceil(32/16) 标量: 2 2
3. Block 0 kcache[0, :, 0, :] [8,16,2,64] [16,64] 见下方K矩阵
读取K
计算Q@K^T q_vec @ k_block.T [64]@[64,16] [16] [3.0, 7.0, 11.0, ...]
↓
scores_0 = [s0, s1, s2, ..., s15]
4. Block 1 kcache[1, :, 0, :] [8,16,2,64] [16,64]
读取K
计算Q@K^T q_vec @ k_block.T [64]@[64,16] [16] [3.4, 7.8, 12.2, ...]
↓
scores_1 = [s16, s17, ..., s31]
5. 拼接scores cat([scores_0, [16],[16] [32] [3.0, 7.0, ..., 7.8]
scores_1])
6. 截断 all_scores[:32] [32] [32] [3.0, 7.0, ..., 7.8]
7. Causal Mask if is_causal: [32] [32] [3.0, 7.0, ..., 3.9, -inf, -inf]
all_scores[31:] = -inf
(假设valid_len=31)
8. Apply Scale all_scores * 0.125 [32] [32] [0.375, 0.875, ..., 0.4875]
9. Softmax max_score = max(scores) [32] 标量: 7.5 7.5
exp_scores = exp( [32] [32] [0.002, 0.018, ..., 1.0, 0, 0]
scores - max_score)
sum_exp = sum( [32] 标量: 1.185 1.185
exp_scores)
weights = exp_scores/ [32] [32] [0.002, 0.015, ..., 0.844, 0, 0]
sum_exp
↓
attn_weights = [w0, w1, ..., w31] (和为1.0)
lse = log(sum_exp) + 标量*2 标量: 8.17 8.17
max_score
10. Block 0 kcache[0,:16,0,:64] [8,16,2,64] [16,64] V矩阵
读取V
加权求和 weights[0:16] @ v [16]@[16,64] [64] 累加到output_vec
↓
output_vec += Σ(w_i * v_i)
11. Block 1 kcache[1,:16,0,:64] [8,16,2,64] [16,64] V矩阵
读取V
加权求和 weights[16:32] @ v [16]@[16,64] [64] 累加到output_vec
↓
output_vec += Σ(w_i * v_i)
12. 存储结果 output[0,0,0] = out [64] - 写入output
softmax_lse[0,0,0]=lse 标量 - 写入softmax_lse
输出: output[0,0,0,:] = [o0, o1, o2, ..., o63]
softmax_lse[0,0,0] = 8.175. 具体数值示例
5.1 Q向量
python
# batch=0, token=0, head=0
q_vec = [1.0, 2.0, 3.0, 4.0] # 简化为4维5.2 K矩阵 (Block 0)
python
k_block = [
[0.1, 0.2, 0.3, 0.4], # token 0
[0.5, 0.6, 0.7, 0.8], # token 1
[0.9, 1.0, 1.1, 1.2], # token 2
[1.3, 1.4, 1.5, 1.6], # token 3
]
形状: [4, 4] # 简化版,实际是[16, 64]5.3 计算Q@K^T
python
# token 0的得分
score_0 = 1.0*0.1 + 2.0*0.2 + 3.0*0.3 + 4.0*0.4
= 0.1 + 0.4 + 0.9 + 1.6
= 3.0
# token 1的得分
score_1 = 1.0*0.5 + 2.0*0.6 + 3.0*0.7 + 4.0*0.8
= 0.5 + 1.2 + 2.1 + 3.2
= 7.0
# token 2的得分
score_2 = 1.0*0.9 + 2.0*1.0 + 3.0*1.1 + 4.0*1.2
= 0.9 + 2.0 + 3.3 + 4.8
= 11.0
# token 3的得分
score_3 = 1.0*1.3 + 2.0*1.4 + 3.0*1.5 + 4.0*1.6
= 1.3 + 2.8 + 4.5 + 6.4
= 15.0
scores = [3.0, 7.0, 11.0, 15.0]物理含义:
- score越大,表示该历史token与当前query越相关
- token 3的得分15.0最高,说明它最相关
5.4 应用Softmax Scale
python
softmax_scale = 0.5 # 假设
scaled_scores = [3.0*0.5, 7.0*0.5, 11.0*0.5, 15.0*0.5]
= [1.5, 3.5, 5.5, 7.5]5.5 Softmax计算
python
# 找最大值
max_score = 7.5
# 减去最大值
scores - max_score = [1.5-7.5, 3.5-7.5, 5.5-7.5, 7.5-7.5]
= [-6.0, -4.0, -2.0, 0.0]
# 计算exp
exp_scores = [exp(-6.0), exp(-4.0), exp(-2.0), exp(0.0)]
≈ [0.0025, 0.0183, 0.1353, 1.0000]
# 求和
sum_exp = 0.0025 + 0.0183 + 0.1353 + 1.0000
≈ 1.1561
# 归一化
weights = [0.0025/1.1561, 0.0183/1.1561, 0.1353/1.1561, 1.0/1.1561]
≈ [0.0022, 0.0158, 0.1170, 0.8650]
总和: 0.0022 + 0.0158 + 0.1170 + 0.8650 = 1.0000 ✓
# 计算LSE
lse = log(1.1561) + 7.5
= 0.1449 + 7.5
= 7.6449物理含义:
- token 3得到86.5%的注意力权重(最高)
- token 0只得到0.22%的权重(几乎忽略)
5.6 V矩阵
python
v_block = [
[0.1, 0.2, 0.3, 0.4], # token 0的V
[0.5, 0.6, 0.7, 0.8], # token 1的V
[0.9, 1.0, 1.1, 1.2], # token 2的V
[1.3, 1.4, 1.5, 1.6], # token 3的V
]
形状: [4, 4]5.7 计算加权和
python
weights = [0.0022, 0.0158, 0.1170, 0.8650]
# 第0维
output[0] = 0.0022*0.1 + 0.0158*0.5 + 0.1170*0.9 + 0.8650*1.3
= 0.00022 + 0.0079 + 0.1053 + 1.1245
= 1.2379
# 第1维
output[1] = 0.0022*0.2 + 0.0158*0.6 + 0.1170*1.0 + 0.8650*1.4
= 0.00044 + 0.00948 + 0.1170 + 1.2110
= 1.3379
# 第2维
output[2] = 0.0022*0.3 + 0.0158*0.7 + 0.1170*1.1 + 0.8650*1.5
= 0.00066 + 0.01106 + 0.1287 + 1.2975
= 1.4379
# 第3维
output[3] = 0.0022*0.4 + 0.0158*0.8 + 0.1170*1.2 + 0.8650*1.6
= 0.00088 + 0.01264 + 0.1404 + 1.3840
= 1.5379
最终输出向量:
output_vec = [1.2379, 1.3379, 1.4379, 1.5379]物理含义:
- 输出向量主要由token 3的V决定(因为它权重最大)
- 其他token的V贡献很小
5.8 多头的情况
对于4个Q头、2个KV头的GQA:
q_head 0 ──┐
q_head 1 ──┴─> 共享 kv_head 0
q_head 2 ──┐
q_head 3 ──┴─> 共享 kv_head 1
每个Q头都会执行上述完整流程,生成自己的output_vec6. 关键代码片段解读
6.1 Q@K^T 计算
python
# 伪代码
for block_idx in range(blk_num):
# 获取物理block索引
kv_block_idx = block_table[b, block_idx]
# 从cache读取K: [page_block_size, head_size]
k_block = kcache[kv_block_idx, :, kv_head_idx]
# Q @ K^T: [head_size] @ [head_size, page_block_size]
# 结果: [page_block_size]
scores_block = torch.matmul(q_vec, k_block.transpose(-2, -1))
attn_scores.append(scores_block)
# 拼接所有block的scores
all_scores = torch.cat(attn_scores, dim=0) # [total_tokens]关键点:
k_block.transpose(-2, -1)将 [16, 64] 转置为 [64, 16]matmul做批量点积: q和每个k向量点积
6.2 Causal Mask
python
if is_causal:
# 当前batch的KV长度: 32
# 当前query序列长度: 2
# causal基准位置: 32 - 2 = 30
causal_base_pos = cur_batch_kv_len - seqlen_q
# 对于query_idx=0,可以看到: 30 + 0 + 1 = 31 个token
valid_len = causal_base_pos + query_idx + 1
# 将后面的设为-inf
all_scores[valid_len:] = -float('inf')图示:
KV Cache: [t0, t1, t2, ..., t29, t30, t31]
↑
Query 0: 可以看到这里以前的所有token
Query 1: 可以看到所有32个token6.3 数值稳定的Softmax
python
# 普通softmax (会溢出):
# exp_scores = exp(scores) # 可能exp(1000)溢出!
# 数值稳定版本:
max_score = torch.max(all_scores)
exp_scores = torch.exp(all_scores - max_score) # 最大值变成0
sum_exp = torch.sum(exp_scores)
attn_weights = exp_scores / sum_exp
# LSE (log-sum-exp)
lse = torch.log(sum_exp) + max_score为什么数值稳定:
exp(score - max_score)保证指数最大是0- 避免
exp(大数)导致溢出 - LSE对于混合精度训练很重要
7. GQA (分组查询注意力) 详解
传统MHA vs GQA
传统MHA (Multi-Head Attention):
Q: 4个头 [q0, q1, q2, q3]
K: 4个头 [k0, k1, k2, k3]
V: 4个头 [v0, v1, v2, v3]
每个Q头独立使用一个KV头
内存占用: 4 * 2 * head_size * seq_len
─────────────────────────────
GQA (Grouped Query Attention):
Q: 4个头 [q0, q1, q2, q3]
K: 2个头 [k0, k1]
V: 2个头 [v0, v1]
分组共享:
Group 0: q0, q1 共享 k0, v0
Group 1: q2, q3 共享 k1, v1
内存占用: 2 * 2 * head_size * seq_len
节省50%内存!代码实现
python
num_queries_per_kv = num_heads_q // num_heads_kv # 4 // 2 = 2
for q_head_idx in range(num_heads_q): # 0, 1, 2, 3
# 计算对应的KV头索引
kv_head_idx = q_head_idx // num_queries_per_kv
# q_head_idx=0 -> kv_head_idx=0
# q_head_idx=1 -> kv_head_idx=0
# q_head_idx=2 -> kv_head_idx=1
# q_head_idx=3 -> kv_head_idx=18. 总结
核心思想
- 分页存储: KV Cache分块存储,支持动态长度
- 批量处理: 同时处理多个请求
- GQA优化: Q头共享KV头,节省内存
- 数值稳定: 使用log-sum-exp技巧
数据流动路径
Q [B,S,H,D]
↓ 提取
q_vec [D]
↓ 与K点积
scores [kv_len]
↓ Mask + Scale
scaled_scores [kv_len]
↓ Softmax
weights [kv_len]
↓ 与V加权求和
output_vec [D]
↓ 存储
output [B,S,H,D]循环层次
for batch (B维)
for query_token (S维)
for query_head (H维)
计算该位置的attention
生成output_vec [D维]性能优化
- FP8量化: 减少内存和计算
- 分块计算: 避免大矩阵乘法
- Causal mask: 节省不必要的计算
完整的流程
┌─────────────────────────────────────────────────────────────────────────────┐
│ 输入层 (Input Layer) │
├─────────────────────────────────────────────────────────────────────────────┤
│ │
│ Q (Query) KV Cache 辅助信息 │
│ [1,1,2,4] [2,4,1,4] │
│ │
│ ┌──────────┐ ┌────────────┐ ┌─────────────┐ │
│ │ [1,2,3,4]│ │ Block 0 │ │seqlens_k: 6 │ │
│ │ [1.5,2.5,│ │ t0:[0.1,..]│ │ │ │
│ │ 3.5,4.5]│ │ t1:[0.5,..]│ │block_table: │ │
│ └──────────┘ │ t2:[0.9,..]│ │ [0, 1] │ │
│ 2个head的 │ t3:[1.3,..]│ └─────────────┘ │
│ query向量 │ │ │
│ │ Block 1 │ │
│ │ t4:[0.2,..]│ │
│ │ t5:[0.6,..]│ │
│ └────────────┘ │
│ 6个历史token │
└─────────────────────────────────────────────────────────────────────────────┘
│
▼
┌─────────────────────────────────────────────────────────────────────────────┐
│ 计算层 (Computation Layer) │
│ for batch × token × head 循环 │
├─────────────────────────────────────────────────────────────────────────────┤
│ │
│ 【步骤1】提取Q向量 │
│ ┌────────────────────────────────────────────────┐ │
│ │ q_vec = Q[0, 0, 0, :] = [1.0, 2.0, 3.0, 4.0] │ │
│ └────────────────────────────────────────────────┘ │
│ │ 形状: [4] │
│ ▼ │
│ 【步骤2】分块计算 Q @ K^T │
│ ┌────────────────────────────────────────────────────────┐ │
│ │ Block 0: scores = [1,2,3,4] @ [0.1,0.2,0.3,0.4]^T │ │
│ │ @ [0.5,0.6,0.7,0.8]^T │ │
│ │ @ [0.9,1.0,1.1,1.2]^T │ │
│ │ @ [1.3,1.4,1.5,1.6]^T │ │
│ │ = [3.0, 7.0, 11.0, 15.0] │ │
│ │ │ │
│ │ Block 1: scores = [1,2,3,4] @ [0.2,0.3,0.4,0.5]^T │ │
│ │ @ [0.6,0.7,0.8,0.9]^T │ │
│ │ = [4.0, 8.0] │ │
│ │ │ │
│ │ 拼接: all_scores = [3, 7, 11, 15, 4, 8] │ │
│ └────────────────────────────────────────────────────────┘ │
│ │ 形状: [6] │
│ ▼ │
│ 【步骤3】应用 Softmax Scale │
│ ┌────────────────────────────────────────────────┐ │
│ │ scaled_scores = [3,7,11,15,4,8] × 0.5 │ │
│ │ = [1.5, 3.5, 5.5, 7.5, 2.0, 4.0] │ │
│ └────────────────────────────────────────────────┘ │
│ │ 形状: [6] │
│ ▼ │
│ 【步骤4】数值稳定的 Softmax │
│ ┌─────────────────────────────────────────────────────────┐ │
│ │ max_score = 7.5 │ │
│ │ exp_scores = exp([1.5-7.5, 3.5-7.5, ..., 4.0-7.5]) │ │
│ │ = [0.0025, 0.0183, 0.1353, 1.0, 0.0041, │ │
│ │ 0.0302] │ │
│ │ sum = 1.1904 │ │
│ │ │ │
│ │ weights = [0.0021, 0.0154, 0.1137, 0.8400, 0.0034, │ │
│ │ 0.0254] │ │
│ │ │ │
│ │ LSE = log(1.1904) + 7.5 = 7.6743 │ │
│ └─────────────────────────────────────────────────────────┘ │
│ │ 形状: [6] │
│ │ 注意力权重 (和为1.0) │
│ ▼ │
│ 【权重分析】 │
│ ┌──────────────────────────────────────┐ │
│ │ token 0: 0.21% ▏ │ │
│ │ token 1: 1.54% ▎ │ │
│ │ token 2: 11.37% ████▏ │ │
│ │ token 3: 84.00% ████████████████████ │ ← 最重要! │
│ │ token 4: 0.34% ▏ │ │
│ │ token 5: 2.54% ▉ │ │
│ └──────────────────────────────────────┘ │
│ │ │
│ ▼ │
│ 【步骤5】分块计算加权和 Attention @ V │
│ ┌──────────────────────────────────────────────────────────┐ │
│ │ output = Σ (weight[i] × V[i]) │ │
│ │ │ │
│ │ Block 0: │ │
│ │ 0.0021×[0.1,0.2,0.3,0.4] = [0.0002,0.0004,0.0006,0.0008]│ │
│ │ + 0.0154×[0.5,0.6,0.7,0.8] = [0.0077,0.0092,0.0108,0.0123]│ │
│ │ + 0.1137×[0.9,1.0,1.1,1.2] = [0.1023,0.1137,0.1251,0.1364]│ │
│ │ + 0.8400×[1.3,1.4,1.5,1.6] = [1.0920,1.1760,1.2600,1.3440]│ │
│ │ │ │
│ │ Block 1: │ │
│ │ + 0.0034×[0.2,0.3,0.4,0.5] = [0.0007,0.0010,0.0014,0.0017]│ │
│ │ + 0.0254×[0.6,0.7,0.8,0.9] = [0.0152,0.0178,0.0203,0.0229]│ │
│ │ │ │
│ │ output_vec = [1.2182, 1.3182, 1.4182, 1.5182] │ │
│ └──────────────────────────────────────────────────────────┘ │
│ │ 形状: [4] │
│ ▼ │
│ 【步骤6】存储结果 │
│ ┌────────────────────────────────────────────────┐ │
│ │ output[0, 0, 0, :] = [1.2182, 1.3182, ...] │ │
│ │ softmax_lse[0, 0, 0] = 7.6743 │ │
│ └────────────────────────────────────────────────┘ │
│ │
└─────────────────────────────────────────────────────────────────────────────┘
│
▼
┌─────────────────────────────────────────────────────────────────────────────┐
│ 输出层 (Output Layer) │
├─────────────────────────────────────────────────────────────────────────────┤
│ │
│ output softmax_lse │
│ [1, 1, 2, 4] [1, 2, 1] │
│ │
│ ┌─────────────────────┐ ┌─────────┐ │
│ │ head 0: [1.22, ...] │ │ 7.6743 │ │
│ │ head 1: [1.50, ...] │ │ 8.0958 │ │
│ └─────────────────────┘ └─────────┘ │
│ 每个head的输出向量 对应的LSE值 │
│ │
└─────────────────────────────────────────────────────────────────────────────┘
bash
================================================================================
FwdKvcacheMla 算子数据流程演示
================================================================================
>>> 参数设置
------------------------------------------------------------
batch_size = 1
seqlen_q = 1
num_heads_q = 2
num_heads_kv = 1
head_size = 4
head_size_v = 4
page_block_size = 4
kv_len = 6
softmax_scale = 0.5
is_causal = False
================================================================================
输入数据准备
================================================================================
>>> 1. Query 张量
------------------------------------------------------------
Q:
形状: (1, 1, 2, 4)
数据类型: float32
示例值: [1. 2. 3. 4. 1.5 2.5 3.5 4.5]
解释:
Q[0,0,0,:] 是 batch 0, token 0, head 0 的查询向量
Q[0,0,1,:] 是 batch 0, token 0, head 1 的查询向量
>>> 2. KV Cache 张量
------------------------------------------------------------
KCache:
形状: (2, 4, 1, 4)
数据类型: float32
示例值: [0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
解释:
kcache[0,:,:,:] 是 Block 0,存储token 0-3
kcache[1,:,:,:] 是 Block 1,存储token 4-7
>>> 3. 序列长度
------------------------------------------------------------
seqlens_k:
形状: (1,)
数据类型: int32
值: [6]
解释: batch 0 有 6 个历史token
>>> 4. 块映射表
------------------------------------------------------------
block_table:
形状: (1, 2)
数据类型: int32
数据 (显示前1行):
行0: [0 1]
解释: batch 0 使用 block 0 和 block 1
================================================================================
计算流程演示
================================================================================
演示位置: batch=0, query_token=0, q_head=0
对应的 kv_head=0 (GQA机制)
>>> 步骤1: 提取Q向量
------------------------------------------------------------
q_vec:
形状: (4,)
数据类型: float32
值: [1. 2. 3. 4.]
这个4维向量将用来和所有历史token的K向量做点积
>>> 步骤2: 计算 Q @ K^T (注意力分数)
------------------------------------------------------------
当前batch的KV长度: 6
需要读取的块数: 2
--- 处理 Block 0 (物理block 0) ---
k_block (Block 0):
形状: (4, 4)
数据类型: float32
数据 (显示前4行):
行0: [0.1 0.2 0.3 0.4]
行1: [0.5 0.6 0.7 0.8]
行2: [0.9 1. 1.1 1.2]
行3: [1.3 1.4 1.5 1.6]
scores (Block 0):
形状: (4,)
数据类型: float32
值: [ 3. 7. 11. 15.]
详细计算:
token 0: q·k = [1. 2. 3. 4.] · [0.1 0.2 0.3 0.4] = 3.00
token 1: q·k = [1. 2. 3. 4.] · [0.5 0.6 0.7 0.8] = 7.00
token 2: q·k = [1. 2. 3. 4.] · [0.9 1. 1.1 1.2] = 11.00
token 3: q·k = [1. 2. 3. 4.] · [1.3 1.4 1.5 1.6] = 15.00
--- 处理 Block 1 (物理block 1) ---
k_block (Block 1):
形状: (4, 4)
数据类型: float32
数据 (显示前4行):
行0: [0.2 0.3 0.4 0.5]
行1: [0.6 0.7 0.8 0.9]
行2: [1. 1.1 1.2 1.3]
行3: [1.4 1.5 1.6 1.7]
scores (Block 1):
形状: (4,)
数据类型: float32
值: [ 4. 8. 12. 16.]
详细计算:
token 4: q·k = [1. 2. 3. 4.] · [0.2 0.3 0.4 0.5] = 4.00
token 5: q·k = [1. 2. 3. 4.] · [0.6 0.7 0.8 0.9] = 8.00
token 6: q·k = [1. 2. 3. 4.] · [1. 1.1 1.2 1.3] = 12.00
token 7: q·k = [1. 2. 3. 4.] · [1.4 1.5 1.6 1.7] = 16.00
>>> 步骤3: 拼接所有block的分数
------------------------------------------------------------
all_scores (拼接后):
形状: (8,)
数据类型: float32
值: [ 3. 7. 11. 15. 4. 8. 12. 16.]
all_scores (截断到实际长度):
形状: (6,)
数据类型: float32
值: [ 3. 7. 11. 15. 4. 8.]
>>> 步骤4: 应用 Softmax Scale
------------------------------------------------------------
softmax_scale = 0.5
scaled_scores:
形状: (6,)
数据类型: float32
值: [1.5 3.5 5.5 7.5 2. 4. ]
>>> 步骤5: Softmax 计算 (数值稳定版)
------------------------------------------------------------
max_score = 7.5000
scores - max_score:
形状: (6,)
数据类型: float32
值: [-6. -4. -2. 0. -5.5 -3.5]
exp(scores - max_score):
形状: (6,)
数据类型: float32
值: [0.0025 0.0183 0.1353 1. 0.0041 0.0302]
sum(exp_scores) = 1.1904
attn_weights (归一化后):
形状: (6,)
数据类型: float32
值: [0.0021 0.0154 0.1137 0.84 0.0034 0.0254]
验证: sum(attn_weights) = 1.000000 (应该=1.0)
LSE = log(sum_exp) + max_score = log(1.1904) + 7.5000 = 7.6743
注意力权重分析:
token 0: 0.0021 (0.21%)
token 1: 0.0154 (1.54%)
token 2: 0.1137 (11.37%)
token 3: 0.8400 (84.00%)
token 4: 0.0034 (0.34%)
token 5: 0.0254 (2.54%)
最重要的token: token 3 (权重 0.8400)
>>> 步骤6: 计算加权和 Attention @ V
------------------------------------------------------------
--- 处理 Block 0 (物理block 0) ---
v_block (Block 0):
形状: (4, 4)
数据类型: float32
数据 (显示前4行):
行0: [0.1 0.2 0.3 0.4]
行1: [0.5 0.6 0.7 0.8]
行2: [0.9 1. 1.1 1.2]
行3: [1.3 1.4 1.5 1.6]
attn_weights (Block 0):
形状: (4,)
数据类型: float32
值: [0.0021 0.0154 0.1137 0.84 ]
weighted_sum (Block 0):
形状: (4,)
数据类型: float32
值: [1.2023 1.2994 1.3965 1.4936]
--- 处理 Block 1 (物理block 1) ---
v_block (Block 1):
形状: (2, 4)
数据类型: float32
数据 (显示前2行):
行0: [0.2 0.3 0.4 0.5]
行1: [0.6 0.7 0.8 0.9]
attn_weights (Block 1):
形状: (2,)
数据类型: float32
值: [0.0034 0.0254]
weighted_sum (Block 1):
形状: (4,)
数据类型: float32
值: [0.0159 0.0188 0.0217 0.0245]
output_vec (最终):
形状: (4,)
数据类型: float32
值: [1.2182 1.3182 1.4182 1.5182]
详细的加权和计算:
output[0] = 0.0021*0.1 + 0.0154*0.5 + 0.1137*0.9 + 0.8400*1.3 + 0.0034*0.2 + 0.0254*0.6
= 1.2182
output[1] = 0.0021*0.2 + 0.0154*0.6 + 0.1137*1.0 + 0.8400*1.4 + 0.0034*0.3 + 0.0254*0.7
= 1.3182
output[2] = 0.0021*0.3 + 0.0154*0.7 + 0.1137*1.1 + 0.8400*1.5 + 0.0034*0.4 + 0.0254*0.8
= 1.4182
output[3] = 0.0021*0.4 + 0.0154*0.8 + 0.1137*1.2 + 0.8400*1.6 + 0.0034*0.5 + 0.0254*0.9
= 1.5182
================================================================================
输出结果
================================================================================
>>> 最终输出
------------------------------------------------------------
output[0, 0, 0, :] = [1.2182 1.3182 1.4182 1.5182]
softmax_lse[0, 0, 0] = 7.6743
物理含义:
- output_vec 是当前query token经过attention后的表示
- 它是所有历史token的V向量的加权和
- 主要由 token 3 贡献 (权重最大)
================================================================================
多头情况演示 (GQA)
================================================================================
对于 num_heads_q=2, num_heads_kv=1 的情况:
q_head 0 ──┐
q_head 1 ──┴─> 共享 kv_head 0
两个Q头都会执行相同的计算流程,但使用不同的q_vec:
q_head 0: q_vec = [1. 2. 3. 4.]
最关注 token 3 (权重 0.8400)
q_head 1: q_vec = [1.5 2.5 3.5 4.5]
最关注 token 3 (权重 0.8960)
================================================================================
总结
================================================================================
关键步骤回顾:
1. 提取Q向量 [head_size]
2. 分块计算 Q@K^T 得到注意力分数 [kv_len]
3. 应用 softmax_scale 缩放分数
4. Softmax归一化得到注意力权重 [kv_len] (和为1)
5. 分块计算加权和 weights@V 得到输出 [head_size_v]
6. 存储输出和LSE值
数据维度变化:
Q [batch, seq_q, heads_q, dim]
↓ 提取
q_vec [dim]
↓ Q@K^T
scores [kv_len]
↓ Softmax
weights [kv_len]
↓ weights@V
output_vec [dim]
↓ 存储
output [batch, seq_q, heads_q, dim]
================================================================================