一、二叉搜索树的概念
二叉搜索树满足以下几点特征:
(1)若它的左子树不为空,则左子树上所有节点的值都小于等于根节点的值;
(2)若它的右子树不为空,则右子树上所有节点的值都大于等于根节点的值;
(3)它的左右子树也为二叉搜索树。
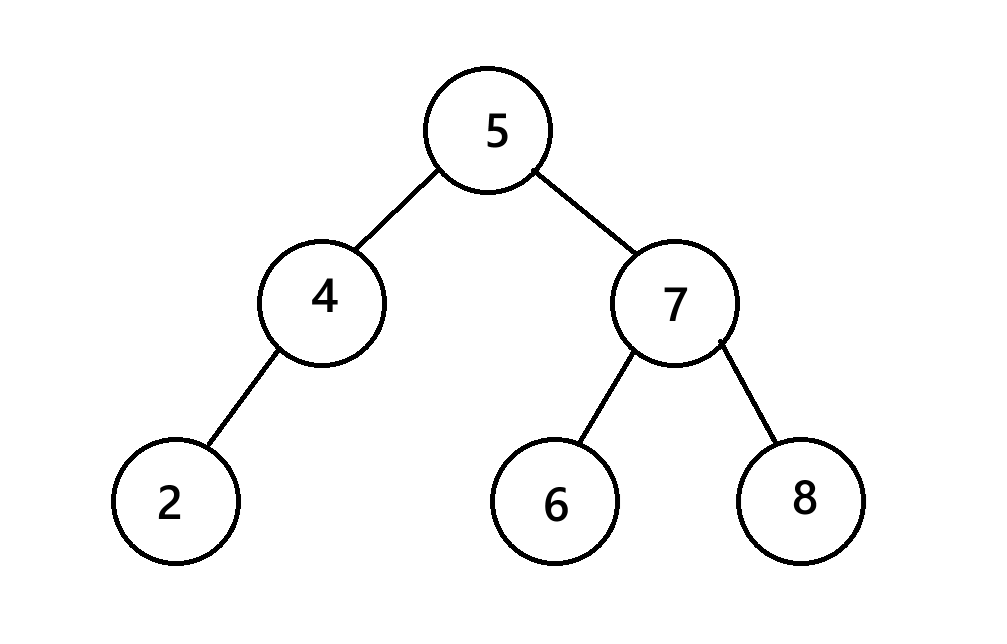
Note:二叉搜索树不要求是完全二叉树。
二、二叉搜索树的性能分析
请思考以下,在二叉搜索树里找一个值的时间复杂度为多少呢?
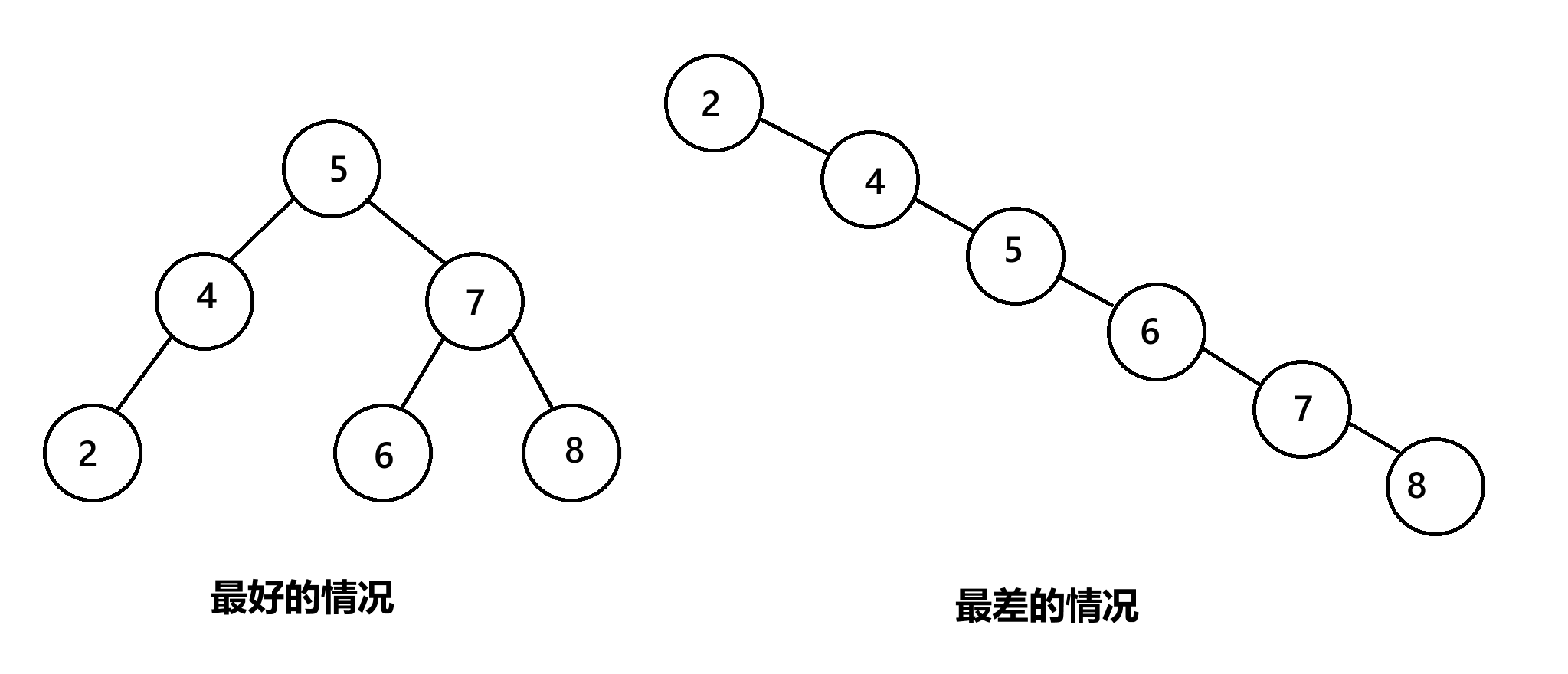
由此图可以清晰得知:最优的情况:O(logN)
最坏的情况:O(N)
所以综上而言。二叉搜索树的时间复杂度为:O(N)
Note:二分查找也能实现时间复杂度为 O(logN),只不过有两个缺陷:
(1)需要存储在支持随机下标访问的结构里,而且还要有序
(2)插入和删除效率低
三、实现搜索二叉树(模拟)
3.1、节点结构
咱们以前学习的二叉树的结点只有一个值,那可不可以有两个值呢?可以的,像后面学习的map 就是如此。简单来说,就是一个节点有两个存放数据的变量:key 和 value ,其中, key 负责比较,value 负责记录一些数据,比如该节点背后的含义等。
cpp
template<class K, class V>
struct BSTreeNode
{
K _key;
V _value;
BSTreeNode* _left;
BSTreeNode* _right;
//构造
BSTreeNode()
:_key(0)
, _value(0)
, _left(nullptr)
, _right(nullptr)
{ }
BSTreeNode(const K& key, const V& value)
:_key(key)
, _value(value)
, _left(nullptr)
, _right(nullptr)
{ }
};那么,在二叉搜索树里的成员变量就只有一个 root,为根节点
3.2、插入(不允许相同的值插入)
很简单,大了我往右边跑,小了我往左边跑。不过不要忘了,如果一开始是一个空树的情况。
cpp
//不允许相等的值插入
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* newnode = new Node(key, value);
Node* parent = nullptr; //parent 为 cur 的父节点
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//到达该插入的结点
if (key > parent->_key)
{
parent->_right = newnode;
}
else
{
parent->_left = newnode;
}
return true;
}Note:为什么要引入一个 parent 节点?因为 cur 节点在循环结束后为 nullptr ,我们应该把 newnode 插入到 cur 的父节点的左右孩子处,而我们的是二叉链表,不能通过孩子找父亲,所以在一开始就引入一个 parent 节点
3.3、查找
这个就很简单了,比大小,大了去右边,小了去左边,如果循环结束还没相等,就返回nullptr
cpp
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (key > cur->_key)
{
cur = cur->_right;
}
else if (key < cur->_key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}3.4、删除(重要)
删除一个节点很简单,但是要保证删除结束后的二叉搜索树结构不被破坏就很难了。我怕们先来分析分析删除一个节点会遇到什么情况:
**第一种情况:**被删除的结点没有左右孩子
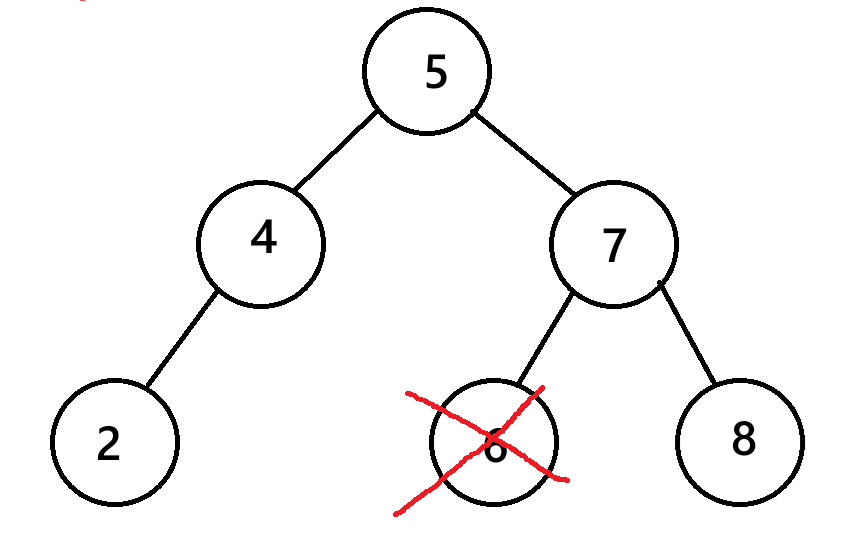
这种情况直接删除就行,对结构没有影响
**第二种情况:**被删除的结点只有一个孩子
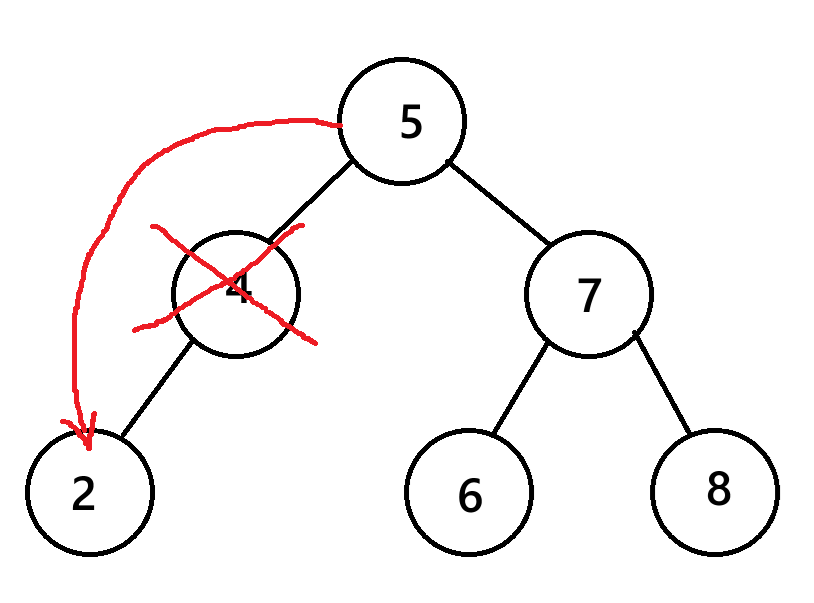
这种情况,由图可知,由它的父节点指向它的孩子即可
**第三种情况:**被删除的结点的左右孩子都存在
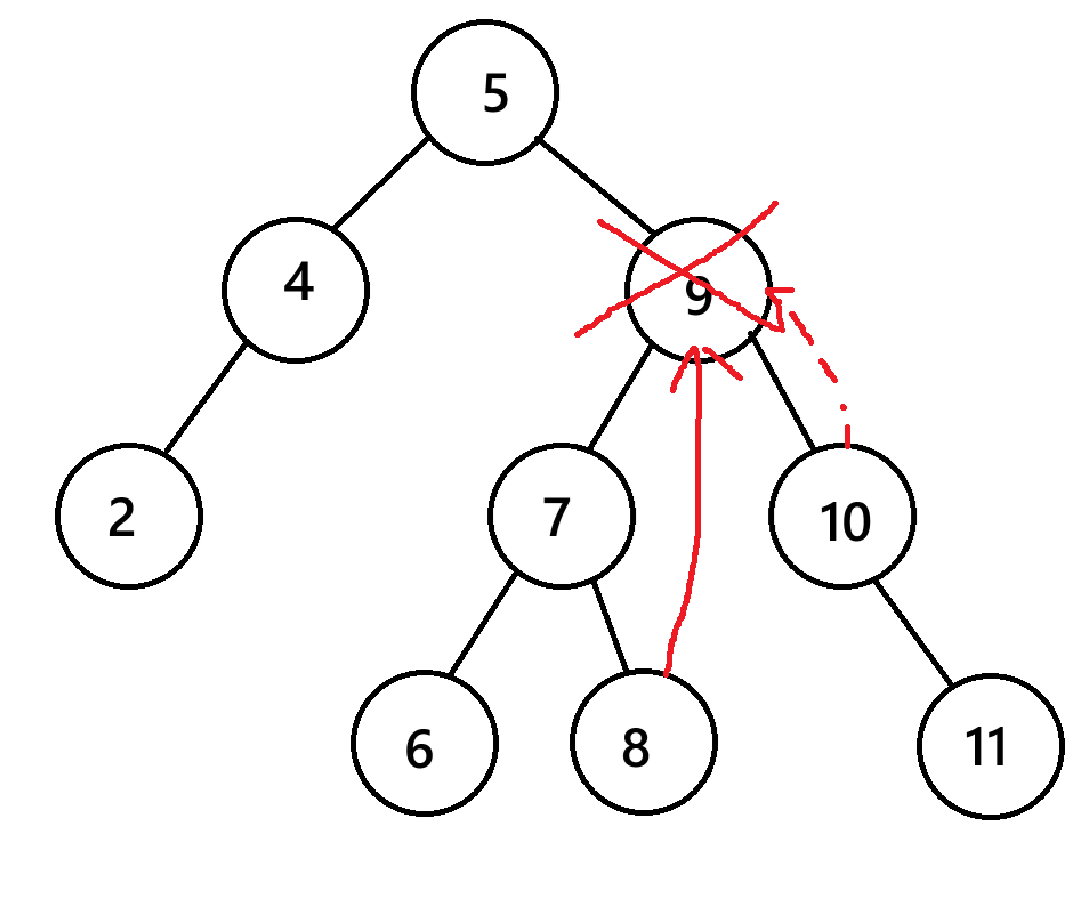
这种情况是最为复杂的,怎么办呢?我们应该在下面寻找一个新的节点代替它的位置,找谁替代?当然是左子树 key 最大的那个或者是右子树 可以 最小的那个。
cpp
bool Erase(const K& key)
{
//首先要找到节点
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (key == cur->_key)
{
//进行删除操作
//cur 的左孩子为空
if (cur->_left == nullptr )
{
if (cur == _root)
{
_root = cur->_right;
delete cur;
cur = nullptr;
}
//cur 是其父节点的左孩子
if (parent->_left = cur)
{
parent->_left = cur->_right;
}
else
{
//cur 是其父节点的右孩子
parent->_right = cur->_right;
}
delete cur;
cur = nullptr;
return true;
}
else if (cur->_right == nullptr )
{
if (cur == _root)
{
_root = cur->_left;
delete cur;
cur = nullptr;
}
//cur 的右孩子为空
if (parent->_left = cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
delete cur;
cur = nullptr;
return true;
}
else
{
//cur的左右孩子都存在
//我们设定寻找右子树的最小值
Node* current = cur->_right;
Node* current_parent = cur;
while (current->_left)
{
current_parent = current;
current = current->_left;
}
cur->_key = current->_key;
cur->_value = current->_value;
if (current_parent->_left == current)
{
current_parent->_left = current->_right;
}
else
{
current_parent->_right = current->_right;
}
delete current;
current = nullptr;
}
}
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
else
{
parent = cur;
cur = cur->_left;
}
}
//走到这里说明未找到
return false;
}Note:为什么没有把 cur 的左右孩子都不存在的情况列出来?因为在其左孩子为空的代码就可以实现这个功能。
满足左孩子为空的情况有两种,左孩子为空右孩子不为空和左右孩子都为空两种情况。
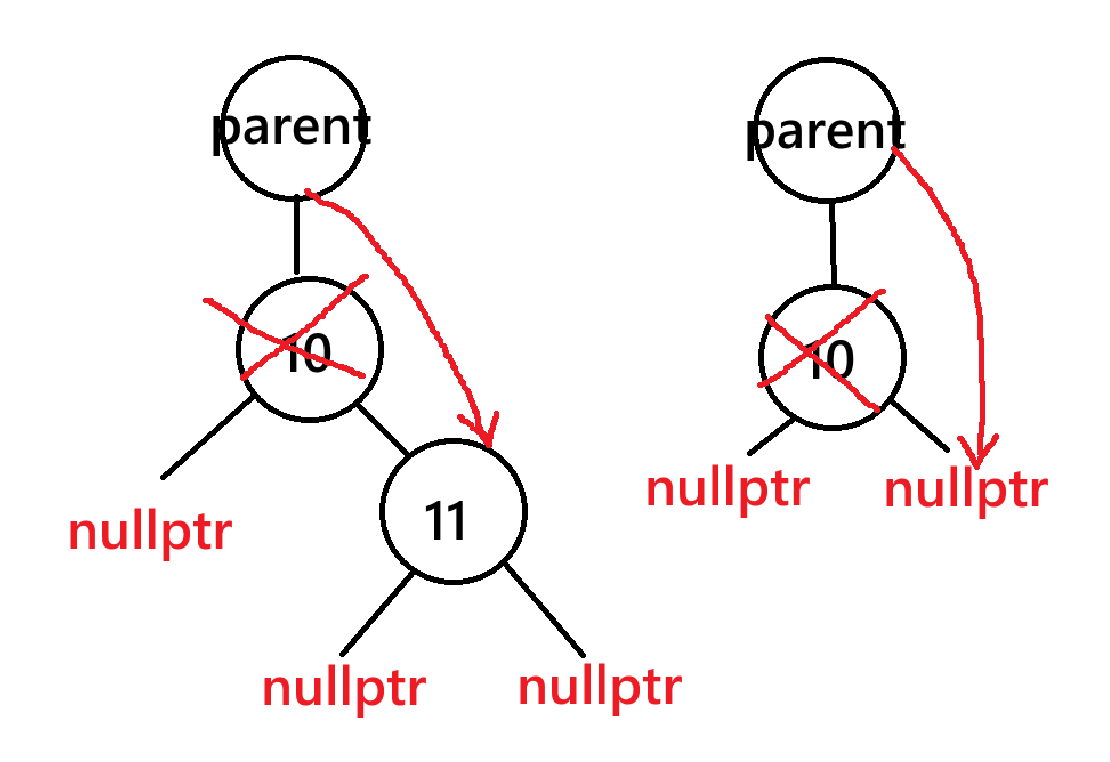
这两种情况都可以满足,在判定 cur 是 parent 的左孩子还是右孩子后,进行删除,只不过第二种情况的右孩子是 nullptr 罢了
恭喜你已经阅读完本篇博客的全部内容,如果有不足和错误,恳请批评和指正,期待我们的下次相会!