计算机视觉（一）：相机标定

1.课程介绍

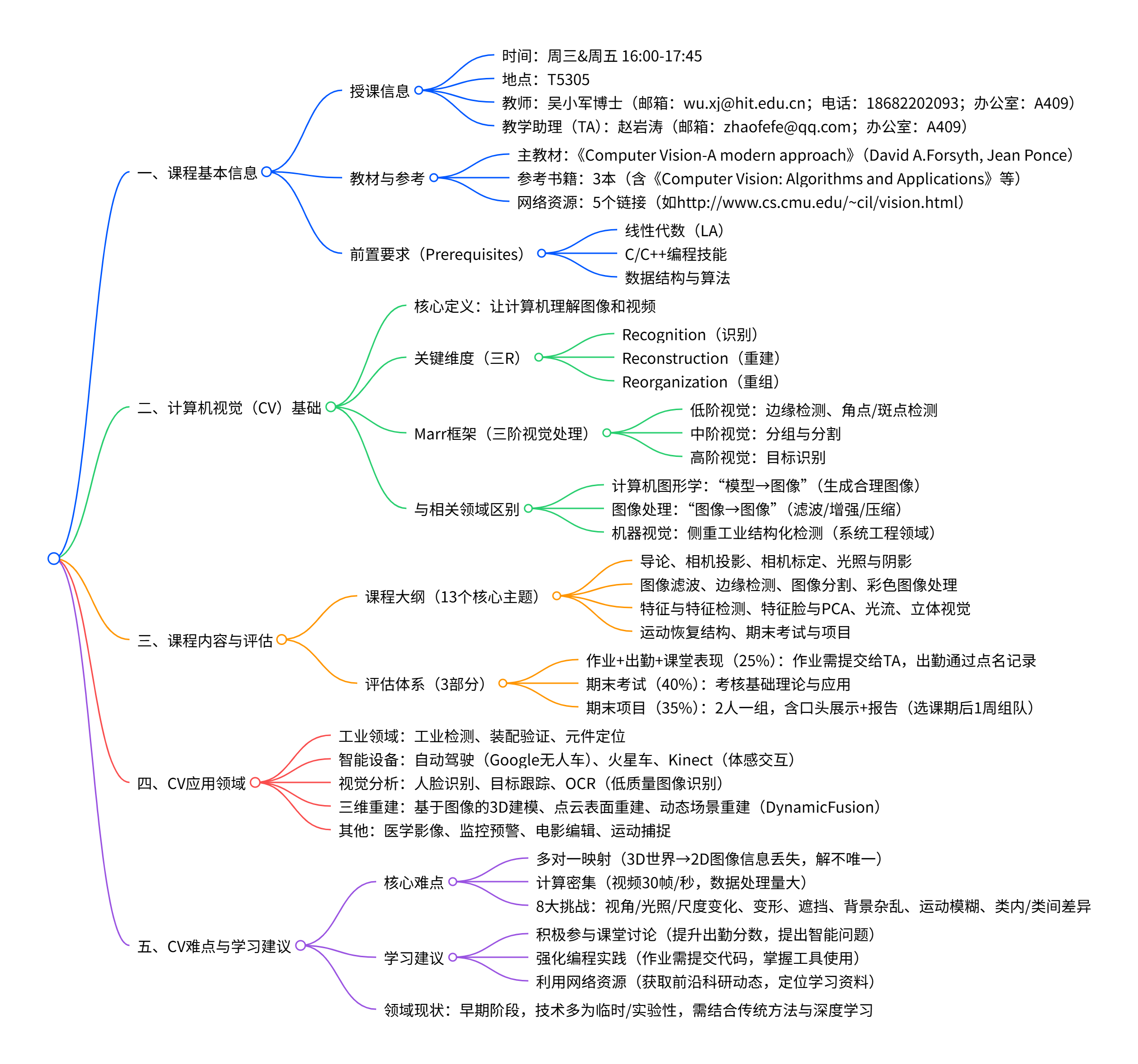
CV的定义是让计算机理解图像和视频 ，核心为"三R（Recognition、Reconstruction、Reorganization）"，并通过Marr框架（低阶边缘检测、中阶分组分割、高阶识别）解析CV流程，同时列举了自动驾驶、3D重建、人脸识别等10+类应用场景 ，指出CV存在多对一映射、计算密集及视角/光照变化等8大挑战，强调其仍处于早期阶段，需结合传统方法与深度学习学习。

思维导图

计算机视觉核心定义与理论框架

CV的核心定义
- 本质：让计算机理解图像和视频 ，具体解决6类问题：
  - 场景识别（"这是什么场景？"）；
  - 目标定位（"汽车在哪里？"）；
  - 距离测量（"建筑物有多远？"）；
  - 行为分析（"它们在做什么？"）；
  - 原因推断（"为什么会发生？"）；
  - 未来预测（"接下来会看到什么？"）。
CV的核心维度------"三R"
- Recognition（识别）：识别图像中的目标与场景；
- Reconstruction（重建）：从2D图像恢复3D场景结构；
- Reorganization（重组）：对图像信息进行结构化整理，支持后续分析。

Marr视觉框架（三阶处理流程）

视觉层级	核心任务	具体操作
低阶视觉（Early Vision）	处理局部图像属性	边缘检测、角点检测、斑点检测
中阶视觉（Mid-level Vision）	图像信息分组	目标分割、区域合并
高阶视觉（High-level Vision）	目标理解	目标识别、场景语义分析

CV与相关领域的区别

领域名称	核心目标	输入输出关系	学科归属
计算机视觉（CV）	从图像中提取定量/定性信息	图像→信息（如目标类别、距离）	计算机科学
计算机图形学	生成"合理"的图像	模型→图像（如3D模型渲染）	计算机科学
图像处理	图像间的转换优化	图像→图像（如滤波、压缩）	信号处理
机器视觉	工业结构化检测任务	图像→检测结果（如缺陷判断）	系统工程

课程大纲

课程核心大纲
1. 计算机视觉导论；
2. 相机模型与投影原理；
3. 相机标定技术；
4. 光照与阴影分析；
5. 图像滤波算法；
6. 边缘检测技术；
7. 图像分割方法；
8. 彩色图像处理；
9. 特征提取与检测；
10. 特征脸（Eigenface）与主成分分析（PCA）；
11. 光流（Optical Flow）估计；
12. 立体视觉（Stereo Vision）；
13. 运动恢复结构（Structure from Motion）

四、CV的应用领域（10+类核心场景）

应用类别	具体案例	技术支撑
工业检测	表面缺陷检测（深度学习驱动）、装配验证、元件计数	机器视觉算法、图像分割
智能交通	自动驾驶（Google无人车，用LIDAR+相机）、车辆跟踪	立体视觉、目标检测、光流
三维重建	基于图像的3D建模（如罗马斗兽场重建）、点云表面重建、动态场景重建（DynamicFusion）	运动恢复结构、激光扫描
生物识别	人脸识别（Face++、百度等企业应用）、微笑快门相机	特征脸、目标跟踪
智能设备	Kinect体感交互（Xbox游戏、Skype视频）、火星车导航	深度相机、立体视觉
医学影像	病灶检测、器官分割	图像分割、特征提取
内容创作	电影特效、运动捕捉（如汤姆·汉克斯数字木偶）	运动捕捉、变形传输
文字识别	低质量图像OCR（深度学习驱动）、代码读取	字符检测、特征匹配

CV的难点

核心难点（3大本质问题+8大挑战）
- 本质多对一映射------不同3D场景（材质、光照、几何）可能生成相似2D图像，导致解不唯一；
- 本质计算密集------视频数据量达30帧/秒，实时处理需求高；
- 8大具体挑战：视角变化、光照变化、尺度变化、目标变形、遮挡、背景杂乱、运动模糊、类内/类间差异。

关键问题

计算机视觉的核心本质是什么？其"三R"维度分别对应哪些具体任务？这些维度如何支撑CV的核心目标？

CV的核心本质是让计算机理解图像和视频，即从2D视觉数据中提取3D场景的语义信息，解决"是什么、在哪里、做什么"等问题；
"三R"维度及具体任务：
- Recognition（识别）：对应"目标/场景识别"任务，如判断图像中的目标是汽车还是建筑、场景是街道还是校园；
- Reconstruction（重建）：对应"3D结构恢复"任务，如从多张图像重建罗马斗兽场的3D模型、通过深度相机获取动态场景的4D（3D+时间）结构；
- Reorganization（重组）：对应"信息结构化"任务，如将图像分割为前景目标与背景、整理目标的轮廓与特征点；
支撑逻辑："三R"形成闭环------Reorganization对图像信息结构化，为Recognition（识别目标）和Reconstruction（重建3D）提供基础，最终共同实现"计算机理解视觉数据"的核心目标。

计算机视觉与图像处理、机器视觉的核心区别是什么？这些区别体现在目标、输入输出关系及学科归属上，对课程学习有何指导意义？

三者核心区别如下表：

对比维度	计算机视觉（CV）	图像处理	机器视觉
核心目标	提取定量/定性信息（如目标类别、距离）	优化图像质量/格式（如去噪、压缩）	解决工业结构化检测（如缺陷判断、装配验证）
输入输出	图像→信息	图像→图像	图像→检测结果（如"合格/不合格"）
学科归属	计算机科学	信号处理	系统工程

2.相机模型

核心围绕"从人眼视觉原理到相机设计与参数"展开：先解析人眼结构 （角膜、瞳孔、晶状体等部件功能及视觉通路）与视觉特性（盲点错觉）；再阐述相机设计演进（从"胶片+屏障"到针孔相机 ，给出最优孔径公式d=2fλd=2\sqrt{f\lambda}d=2fλ ）；随后详解透镜相机核心参数 （焦距计算f=vD/Vf=vD/Vf=vD/V或f=hD/Hf=hD/Hf=hD/H、视场与焦距负相关、F值与光圈的关系、景深影响因素、曝光的"光圈+快门速度"控制、透镜畸变类型）；对比CCD与CMOS感光元件 的9项关键指标（如CCD功耗高但低光灵敏度好，CMOS成本低且速度快）；最后定义5个参考坐标系（物体、世界、相机、图像平面、像素）及相互转换关系，为3D场景分析提供坐标基础。

思维导图

详细总结

人眼结构与视觉原理（相机设计的生物基础）

核心部件及功能

人眼是相机设计的灵感来源，各部件分工明确，共同实现光线感知与成像：

部件名称	核心功能	关键特性
角膜（Cornea）	汇聚入射光线	透明无血管，光线进入眼的第一道"透镜"
瞳孔（Pupil）	调节进光量	虹膜中央孔洞，亮环境缩小（减少强光损伤）、暗环境扩大（增加进光）
晶状体（Lens）	聚焦光线到视网膜	透明可弯曲，通过形状变化调整焦距（如看近物时变凸）
玻璃体（Vitreous）	维持眼球形态	透明粘稠物质，占眼球体积2/3，填充视网膜与晶状体之间的空间
视网膜（Retina）	感光并转换信号	含视杆细胞（弱光感知，无色彩）和视锥细胞（色彩感知，强光下工作），感光细胞位于视网膜底层，光线需穿透血管、神经纤维等多层结构才能到达
脉络膜（Choroid）	营养供给+防反射	富含血管，为视网膜细胞供能；含色素使视网膜呈黑色，避免眼内光线反射导致成像模糊
巩膜（Sclera）	保护眼球	不透明纤维外层，为眼肌提供附着点，维持眼球结构稳定

视觉特性与通路
- 视觉通路：超半数大脑区域参与视觉处理，处理过程高度模块化（从感光细胞→双极细胞→神经节细胞→视神经→大脑视觉皮层）；
- 视觉错觉：存在盲点（视神经穿出视网膜的区域无感光细胞，无法感知光线），但大脑会通过周边视觉信息"补全"盲点，使人难以察觉。

相机设计演进（从"模糊"到"针孔成像"）

初始设计思路的缺陷与改进
- 想法1：直接在物体前方放置胶片→图像严重模糊（原因：物体各点发出的光线杂乱投射到胶片，无定向性）；
- 想法2：在胶片与物体间加"带孔径的屏障"→减少杂光，降低模糊（孔径限制了光线投射方向，使物体各点光线大致对应胶片上的固定点），此时"孔径"即相机的雏形光圈。
针孔相机（Camera Obscura）的核心原理与局限
- 历史起源：公元前5世纪，亚里士多德与中国墨子分别记录了"针孔成像"现象，是最早的相机原型；
- 成像特点：通过极小孔径（针孔）使光线定向投射到胶片，形成倒立实像；
- 关键问题：孔径并非越小越好
  - 过小缺陷：①进光量急剧减少，需长时间曝光；②衍射效应增强（光线绕过小孔边缘发生弯曲），导致图像模糊；
  - 最优孔径公式：d=2fλ\boldsymbol{d=2\sqrt{f\lambda}}d=2fλ （ddd为孔径直径，fff为针孔到胶片的距离，λ\lambdaλ为入射光波长）；
  - 示例计算：若f=50mmf=50mmf=50mm（针孔到胶片距离）、λ=600nm\lambda=600nmλ=600nm（红光波长，1nm=10−6mm1nm=10^{-6}mm1nm=10−6mm），则d=250×600×10−6≈0.346mmd=2\sqrt{50\times600\times10^{-6}}≈0.346mmd=250×600×10−6 ≈0.346mm，此孔径下成像最清晰；
- 实际案例：Jerry Vincent的针孔相机拍摄人像（因曝光时间长，人物移动导致"鬼影"效果）、南安普顿大学Greg Parker的易拉罐针孔相机（拍摄夏至/冬至日轨，记录太阳运动轨迹）。

透镜相机核心参数（决定成像质量的关键）

透镜相机通过"透镜"替代针孔，解决了针孔相机进光量少、衍射模糊的问题，其核心参数直接影响成像效果：

焦距（f）：决定"拍摄范围"的基础
- 定义：透镜中心到成像平面（CCD）的距离，是衡量透镜"聚光能力"的指标；
- 计算公式：基于物体尺寸、物距与CCD尺寸推导，有两个核心公式：
  f=v×D/V\boldsymbol{f=v\times D/V}f=v×D/V
  （垂直方向：vvv为CCD垂直尺寸，DDD为物体到透镜的距离，VVV为物体垂直高度）
  f=h×D/H\boldsymbol{f=h\times D/H}f=h×D/H
  （水平方向：hhh为CCD水平尺寸，HHH为物体水平宽度）；
- CCD尺寸标准（不同格式的传感器尺寸，单位：mm）：
  
  CCD格式垂直尺寸（v）水平尺寸（h）
  
  1型 9.6 12.8
  
  2/3型 6.6 8.8
  
  1/3型 3.6 4.8
  
  1/4型 2.7 3.6
- 焦距选择原则：若垂直/水平方向计算的焦距值不同，取较小值（可获得更大的视场，拍摄范围更广）。
视场（FOV）：与焦距负相关的"拍摄角度"
- 定义：相机能拍摄到的空间范围（以角度衡量），直接决定"一张照片能装下多少景物"；
- 与焦距的关系：焦距越长，视场越小（长焦镜头拍远处小范围，广角镜头拍近处大范围）；
- 典型对应关系（焦距→视场）：
  500mm→5°、135mm→18°、50mm→46°、24mm→83°、7.5mm→180°（鱼眼镜头）。
F值（光圈系数）：控制"进光量"的核心
- 定义：衡量光圈大小的指标，公式为#=f/d\boldsymbol{\#=f/d}#=f/d（ddd为光圈直径）；
- 光圈序列：常用F值从大到小为f/22、f/11、f/8、f/5.6、f/4、f/3.5、f/2.8、f/1.4，相邻F值的进光量相差1倍（如从f/2.8到f/4，进光量减半）；
- 核心影响：低F值（如f/1.4）→光圈大→进光多（适合暗环境）；高F值（如f/22）→光圈小→进光少（适合亮环境）。
景深（DoF）：决定"清晰范围"的关键
- 定义：被摄物体中"成像清晰的距离范围"，超出该范围的景物会虚化；
- 影响因素：①物距（物体越远，景深越大）；②焦距（焦距越长，景深越小）；③F值（F值越高，景深越大）；④弥散圆标准（传感器尺寸越小，弥散圆阈值越小，景深越大）；
- 示例对比：
  - f/32（高F值）：景深大，背景与主体均清晰，易导致背景"争夺视觉注意力"；
  - f/5.6（中F值）：景深小，背景虚化，主体（如花朵）更突出。
曝光：控制"成像亮度"的平衡
- 定义：CCD传感器接收的光量总和，直接决定照片"过亮"（过曝）或"过暗"（欠曝）；
- 控制参数：由"光圈（F值）"和"快门速度"共同决定：
  - 快门速度：光线照射CCD的时间（单位：秒的分数，如1/15s、1/60s、1/250s、1/1000s）；
  - 速度影响：慢快门（1/15s）→进光多，但易产生运动模糊 （适合拍流水、夜景）；快快门（1/1000s）→进光少，但能冻结运动（适合拍运动的动物、运动员）。
透镜畸变：透镜不完美导致的"成像偏差"
- 类型：①无畸变（理想透镜，仅理论存在）；②桶形畸变（图像边缘向外凸起，常见于广角镜头）；③枕形畸变（图像边缘向内凹陷，常见于长焦镜头）；
- 原因：透镜镜片曲率加工不完美，边缘光线的折射角度与中心光线偏差过大，导致成像变形。

CCD格式	垂直尺寸（v）	水平尺寸（h）
1型	9.6	12.8
2/3型	6.6	8.8
1/3型	3.6	4.8
1/4型	2.7	3.6

感光元件：CCD与CMOS的差异与应用

感光元件是相机的"视网膜"，负责将光信号转换为电信号，主流类型为CCD（电荷耦合器件）和CMOS（互补金属氧化物半导体），二者在性能与应用上差异显著：

对比维度	CCD（电荷耦合器件）	CMOS（互补金属氧化物半导体）
功耗（Power Consumption）	高	低
噪声（Noise）	低（成像更纯净）	高（易产生杂色噪点）
低光灵敏度（Low light Sensitivity）	好（暗环境成像清晰）	差（暗环境易欠曝、噪点多）
成本（Cost）	高	低
均匀性（Uniformity）	高（画面亮度一致）	低（边缘易偏暗）
速度（Speed）	慢（信号传输慢）	快（每个像素独立处理信号）
动态范围（Dynamic Range）	高（明暗细节保留多）	低（明暗对比强烈时易丢失细节）
开窗功能（Windowing）	不能（需读取全画面）	能（仅读取指定区域，提速）
响应度（Responsivity）	高（光信号转换效率高）	低（转换效率低）

应用场景 ：
- CCD：用于高端相机（如专业单反、工业检测相机），追求高成像质量、低噪声、高灵敏度；
- CMOS：用于低端便携相机（如手机相机、入门级卡片机），优先考虑低功耗（延长续航）、低成本（降低售价）。

参考坐标系与转换（3D场景分析的基础）

为实现"3D场景→2D图像"的精准映射，需定义5个参考坐标系，并明确其转换关系，支撑后续相机标定、立体视觉等技术：

5个核心坐标系的定义

坐标系名称	维度	符号表示	核心用途	关键特性
物体坐标系	3D	(XO,YO,ZO)T(X_O,Y_O,Z_O)^T(XO,YO,ZO)T	建模单个物体（如检测零件孔位相对位置）	坐标不随物体在场景中的位置变化
世界坐标系	3D	(XW,YW,ZW)T(X_W,Y_W,Z_W)^T(XW,YW,ZW)T	关联3D场景中多个物体（如定位"车"与"路"）	全局基准坐标系，固定不变
相机坐标系	3D	(XC,YC,ZC)T(X_C,Y_C,Z_C)^T(XC,YC,ZC)T	以相机为基准描述物体位置	原点为相机投影中心，光轴为Z轴
图像平面坐标系	2D	(x,y)T(x,y)^T(x,y)T	描述3D点在CCD上的投影位置	单位为mm（物理尺寸），原点为主点
像素坐标系	2D	(xim,yim)T(x_{im},y_{im})^T(xim,yim)T	描述像素在图像阵列中的位置	单位为"像素"（整数），原点为图像左上角

关键坐标转换关系
- 图像平面坐标系→像素坐标系（物理尺寸→像素尺寸）：
  因CCD的物理尺寸（如n mm×m mm）与像素阵列尺寸（如N像素×M像素）不同，转换公式为：
  xim=Nnx\boldsymbol{x_{im}=\frac{N}{n}x}xim=nNx
  yim=Mmy\boldsymbol{y_{im}=\frac{M}{m}y}yim=mMy
  （NNN为像素阵列水平尺寸，nnn为CCD水平物理尺寸；MMM为像素阵列垂直尺寸，mmm为CCD垂直物理尺寸，原点均为左上角）。
世界坐标系与相机坐标系的简化假设

为简化3D→2D投影的数学计算，通常做以下假设：
- 相机投影中心与世界坐标系原点重合；
- 相机光轴与世界坐标系Z轴对齐，X/Y轴分别与世界坐标系X/Y轴平行；
- 图像平面位于投影中心前方（避免传统针孔相机的"倒立图像"，简化后续处理）；
- 图像平面原点为主点（principal point） ------光轴与图像平面的交点，注意：主点不一定是图像的几何中心（受透镜安装偏差影响）。

关键问题

针孔相机的"最优孔径"是如何确定的？请结合公式与示例说明其原理，以及孔径过小会导致什么问题？

针孔相机的最优孔径由"进光量"与"衍射模糊"的平衡决定，核心是通过公式计算使成像最清晰：

最优孔径公式 ：d=2fλ\boldsymbol{d=2\sqrt{f\lambda}}d=2fλ ，其中ddd为孔径直径（mm），fff为针孔到胶片的距离（mm），λ\lambdaλ为入射光的波长（mm，如红光λ=600nm=600×10−6mm\lambda=600nm=600\times10^{-6}mmλ=600nm=600×10−6mm）；
示例计算 ：若针孔到胶片距离f=50mmf=50mmf=50mm，红光波长λ=600nm\lambda=600nmλ=600nm，代入公式得：
d=250×600×10−6=20.03=2×0.173≈0.346mmd=2\sqrt{50\times600\times10^{-6}}=2\sqrt{0.03}=2\times0.173≈0.346mmd=250×600×10−6 =20.03 =2×0.173≈0.346mm

即孔径直径为0.346mm时成像最清晰；
孔径过小的问题：

①进光量不足------光线仅能通过极小孔洞，需延长曝光时间（如拍摄动态物体时易产生模糊）；

②衍射效应增强------光线绕过小孔边缘发生弯曲，导致物体各点的投影光斑扩大，图像整体模糊。

透镜相机的"焦距""视场""F值"三者之间存在怎样的关联？这些关联对实际拍摄（如人像、风景）有何指导意义？

三者的核心关联的是"焦距为基础，视场与焦距负相关，F值通过光圈间接影响成像范围的清晰度"，具体关联及拍摄指导如下：

焦距与视场的关联 ：焦距越长，视场越小 （焦距决定"镜头能'看'多远"，视场决定"镜头能'看'多广"）；
- 典型对应：500mm长焦→5°视场（仅拍远处小物体，如月亮）；24mm广角→83°视场（拍大范围场景，如风景）；50mm标准焦→46°视场（接近人眼视角，拍日常场景）；
焦距与F值的关联 ：F值由"焦距/光圈直径"（#=f/d\#=f/d#=f/d）决定，相同光圈直径下，焦距越长，F值越高（进光量越少）；
对实际拍摄的指导 ：
- 人像拍摄：选50-85mm中长焦（视场适中，压缩背景空间感）+低F值（如f/1.8-f/4，背景虚化突出人物）；
- 风景拍摄：选16-24mm广角（大视场容纳更多景物）+高F值（如f/8-f/16，大景深确保远近景物均清晰）；
- 夜景拍摄：选24-50mm标准焦（平衡视场与手抖影响）+低F值（如f/2.8-f/5.6，增加进光量，减少噪点）。

CCD与CMOS作为两种主流感光元件，在"低光灵敏度""功耗""成本"三个关键维度上有何差异？这些差异如何决定它们的应用场景？

CCD与CMOS在三个维度的差异显著，直接决定了其适用的相机类型：

核心差异对比 ：

维度	CCD	CMOS
低光灵敏度	好（暗环境下感光能力强，成像清晰、噪点少）	差（暗环境下易欠曝，噪点多、细节丢失）
功耗	高（信号需逐行传输，耗电多）	低（每个像素独立处理信号，耗电少）
成本	高（制造工艺复杂，量产难度大）	低（工艺简单，可与其他电路集成）

应用场景决定 ：
- CCD的应用：高端相机（如专业单反相机、工业检测相机、天文相机）------这类场景优先追求"成像质量"（低光清晰、低噪点），对功耗和成本敏感度低；例如工业检测中，需在暗箱内拍摄零件缺陷，CCD的低光灵敏度可确保缺陷细节不丢失；
- CMOS的应用：低端便携设备（如手机相机、入门级卡片机、监控摄像头）------这类场景优先考虑"续航"（低功耗延长使用时间）和"售价"（低成本降低用户购买门槛），对成像质量要求适中；例如手机相机需集成在狭小空间内，CMOS的低功耗和小体积优势显著，同时满足日常拍照需求。

3.相机参数与投影原理

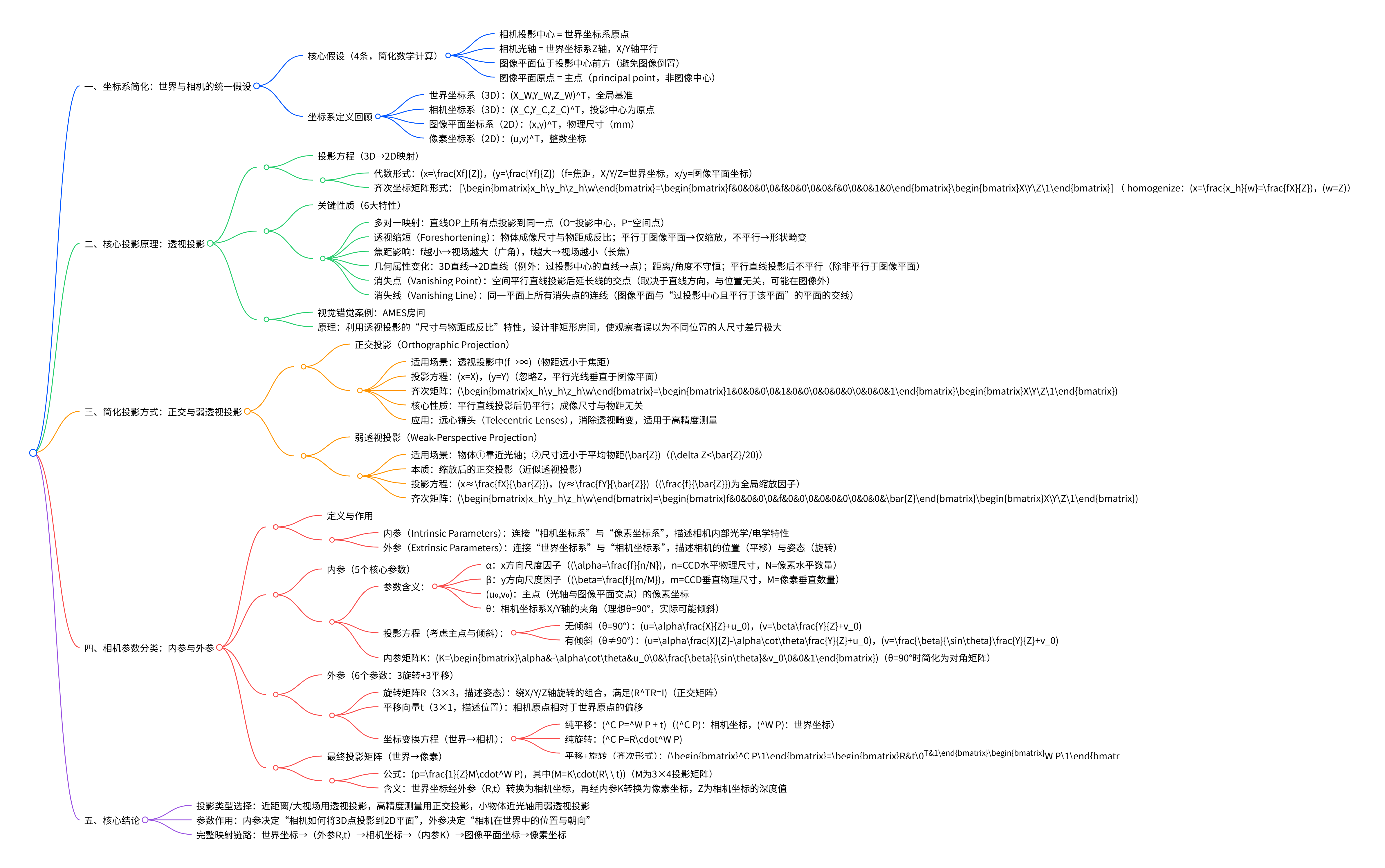
核心围绕"3D场景到2D像素的映射过程"展开：先通过4个简化假设（投影中心与世界原点重合、光轴对齐世界Z轴等）统一世界与相机坐标系；随后详解透视投影 的代数/矩阵（齐次坐标）方程及关键性质（多对一映射、透视缩短、消失点/消失线，附AMES房间视觉错觉案例）；对比两种简化投影（正交投影 ：焦距→∞，平行线条投影后仍平行，适用于远心镜头测量；弱透视投影 ：近似透视，适用于物体近光轴且尺寸远小于物距）；最终明确相机参数分类------内参（连接相机与像素坐标系，含尺度因子α/β、主点u₀/v₀、轴夹角θ）与外参（定义相机相对世界的姿态，含旋转矩阵R、平移向量t），并推导内参投影矩阵与外参坐标变换（平移+旋转）的组合形式，最终形成"世界坐标→相机坐标（外参）→图像平面（内参）→像素坐标"的完整映射链路。

思维导图

详细总结

坐标系简化：世界与相机的统一基础

为降低"3D世界→2D图像"映射的数学复杂度，文档提出4条核心简化假设，将世界坐标系与相机坐标系对齐，为后续投影方程推导奠定基础：

投影中心重合：相机的投影中心（透镜中心）与世界坐标系的原点重合；
光轴对齐：相机的光轴（垂直于图像平面的直线）与世界坐标系的Z轴完全一致，且相机坐标系的X/Y轴分别与世界坐标系的X/Y轴平行；
图像平面前置 ：将图像平面（CCD/CMOS所在平面）置于投影中心前方（而非传统针孔相机的后方），避免成像倒置，简化后续处理；
主点为原点 ：图像平面的坐标原点定义为"主点"（光轴与图像平面的交点），需注意：主点不一定是图像的几何中心（受透镜安装偏差影响）。

此阶段需明确4个关键坐标系的角色：世界坐标系（全局基准）、相机坐标系（3D投影起点）、图像平面坐标系（物理尺寸，mm）、像素坐标系（整数坐标，用于显示），后续所有投影与参数均围绕这4个坐标系的转换展开。

核心投影原理：透视投影（Perspective Projection）

透视投影是最贴近人眼与相机成像的模型，文档从方程推导、核心性质、视觉案例三方面展开，是本章重点内容。

1. 投影方程（3D→2D的数学映射）

基于坐标系简化假设，空间中任意一点P(X,Y,Z)P(X,Y,Z)P(X,Y,Z)（世界坐标，因坐标系对齐，等同于相机坐标）在图像平面上的投影点p(x,y)p(x,y)p(x,y)满足：

代数形式 ：通过相似三角形推导（△OAB∽△OA'B'，O为投影中心，AB为物体尺寸，A'B'为投影尺寸），得到：
x=XfZ,y=YfZ\boldsymbol{x=\frac{Xf}{Z}},\quad\boldsymbol{y=\frac{Yf}{Z}}x=ZXf,y=ZYf
其中，fff为焦距（投影中心到图像平面的距离），ZZZ为点PPP到投影中心的深度（沿光轴方向）。
齐次坐标矩阵形式 ：为统一处理"无穷远点"（如消失点），引入齐次坐标（4维），投影矩阵为： $xhyhzhw\]=\[f0000f0000f00010\]\[XYZ1\]\\begin{bmatrix}x_h\\\\y_h\\\\z_h\\\\w\\end{bmatrix}=\\begin{bmatrix}f\&0\&0\&0\\\\0\&f\&0\&0\\\\0\&0\&f\&0\\\\0\&0\&1\&0\\end{bmatrix}\\begin{bmatrix}X\\\\Y\\\\Z\\\\1\\end{bmatrix} xhyhzhw = f0000f0000f10000 XYZ1 齐次坐标转换为非齐次坐标时，需除以w=Zw=Zw=Z，还原为代数形式：x=xhw=fXZx=\\frac{x_h}{w}=\\frac{fX}{Z}x=wxh=ZfX，y=yhw=fYZy=\\frac{y_h}{w}=\\frac{fY}{Z}y=wyh=ZfY。$

透视投影的特性直接决定了成像效果，也是计算机视觉中"3D重建、相机标定"的关键依据：

性质1：多对一映射
空间中所有位于"过投影中心的直线OP"上的点，投影到图像平面后均为同一点ppp（深度信息Z丢失，导致3D→2D的信息损失）。
性质2：透视缩短（Foreshortening）
物体的成像尺寸与"物体到相机的距离Z"成反比：距离越远，成像越小；若物体表面不平行于图像平面，会产生"形状畸变"（如倾斜的桌面投影后呈梯形）；若平行于图像平面，则仅发生"缩放"（无畸变）。
性质3：焦距对於视场的影响
焦距fff与视场（FOV）呈负相关 ：
- fff越小（广角镜头）：视场越大，能拍摄更多场景，但透视畸变越明显；
- fff越大（长焦镜头）：视场越小，仅能拍摄局部场景，但透视畸变越弱（近似"望远镜"效果）。
性质4：几何属性不守恒
- 3D空间中的直线投影后仍为2D直线（例外：过投影中心的直线投影为点）；
- 距离、角度不守恒（如正方形投影后可能为梯形，直角投影后可能为锐角/钝角）；
- 平行直线投影后不平行（除非直线平行于图像平面），而是汇聚于"消失点"。
性质5：消失点（Vanishing Point）
空间中平行的直线 ，其透视投影的延长线会交于图像平面上的同一点，该点称为"消失点"。
- 关键特性：消失点仅与直线的方向有关，与直线的位置无关；若直线方向平行于光轴，消失点会落在图像平面外（无穷远处）。
性质6：消失线（Vanishing Line）
空间中同一平面上的所有直线 ，其消失点会构成一条直线，称为"消失线"。
- 几何意义：消失线是"过投影中心且平行于该平面"的平面，与图像平面的交线；例如，地面的消失线对应"地平线"。

3. 视觉错觉案例：AMES房间

通过"AMES房间"案例直观展示透视投影的特性：该房间实际为非矩形（墙面、地面均为梯形），但从特定角度观察时，其透视投影与"矩形房间"完全一致，导致观察者误以为房间内不同位置的人"尺寸差异极大"（近处人显小、远处人显大），本质是利用了"透视缩短"与"消失点"的视觉原理。

简化投影方式：正交与弱透视投影

透视投影的数学复杂度较高，在特定场景下可采用正交投影 或弱透视投影简化，文档详细对比了两种模型的适用场景、方程与性质。

1. 正交投影（Orthographic Projection）

适用场景 ：当物体到相机的距离远大于物体尺寸（即焦距f→∞f→∞f→∞），此时透视效应可忽略，如卫星遥感、高精度测量。
核心假设 ：投影光线为平行光，且垂直于图像平面。
投影方程 ：忽略深度Z的影响，直接映射：
x=X,y=Y\boldsymbol{x=X},\quad\boldsymbol{y=Y}x=X,y=Y

齐次矩阵形式：[xhyhzhw]=[1000010000000001][XYZ1]\begin{bmatrix}x_h\\y_h\\z_h\\w\end{bmatrix}=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} xhyhzhw = 1000010000000001 XYZ1

（ homogenize后x=X,y=Yx=X,y=Yx=X,y=Y）。
关键性质：
- 空间中平行的直线，投影后仍平行；
- 物体成像尺寸与"物距"无关（无透视缩短）；
- 无深度信息丢失（但实际应用中仍需额外手段获取Z）。
典型应用 ：远心镜头（Telecentric Lenses） ------通过在透镜焦点处放置小孔，确保投影光线平行，消除透视畸变，适用于工业零件尺寸测量（如螺丝直径、芯片引脚间距）。

2. 弱透视投影（Weak-Perspective Projection）

适用场景 ：物体①靠近相机光轴；②尺寸远小于其到相机的平均距离Zˉ\bar{Z}Zˉ（通常要求δZ<Zˉ/20\delta Z<\bar{Z}/20δZ<Zˉ/20），如小物体（昆虫、零件）的成像。
本质：近似的透视投影，用"缩放后的正交投影"替代，平衡精度与计算复杂度。
投影方程 ：将深度Z近似为平均距离Zˉ\bar{Z}Zˉ，引入全局缩放因子fZˉ\frac{f}{\bar{Z}}Zˉf：
x≈fXZˉ,y≈fYZˉ\boldsymbol{x≈\frac{fX}{\bar{Z}}},\quad\boldsymbol{y≈\frac{fY}{\bar{Z}}}x≈ZˉfX,y≈ZˉfY
齐次矩阵形式：[xhyhzhw]=[f0000f000000000Zˉ][XYZ1]\begin{bmatrix}x_h\\y_h\\z_h\\w\end{bmatrix}=\begin{bmatrix}f&0&0&0\\0&f&0&0\\0&0&0&0\\0&0&0&\bar{Z}\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} xhyhzhw = f0000f000000000Zˉ XYZ1 （ homogenize后x=fXZˉ,y=fYZˉx=\frac{fX}{\bar{Z}},y=\frac{fY}{\bar{Z}}x=ZˉfX,y=ZˉfY）。
关键性质：精度低于透视投影，但计算量远小于透视投影，是计算机视觉中"小物体识别"（如细胞检测）的常用模型。

四、相机参数分类：内参与外参（3D→2D的关键桥梁）

相机参数是"世界坐标→像素坐标"映射的核心，文档将其分为内参（相机内部特性）与外参（相机外部姿态），明确了各参数的定义、方程与矩阵形式。

1. 内参（Intrinsic Parameters）：相机的"内在属性"

内参描述相机自身的光学与电学特性，连接"相机坐标系"与"像素坐标系"，共5个核心参数，决定了3D点如何在图像平面上形成像素。

内参符号	参数名称	物理含义
α	x方向尺度因子	焦距f除以"像素水平物理尺寸"（α=fn/N\alpha=\frac{f}{n/N}α=n/Nf，n=CCD水平尺寸，N=水平像素数）
β	y方向尺度因子	焦距f除以"像素垂直物理尺寸"（β=fm/M\beta=\frac{f}{m/M}β=m/Mf，m=CCD垂直尺寸，M=垂直像素数）
(u₀,v₀)	主点的像素坐标	光轴与图像平面交点的像素位置（理想为图像中心，实际因安装偏差可能偏移）
θ	相机X/Y轴的夹角	理想情况下θ=90°（正交），实际镜头制造误差可能导致θ≠90°（倾斜）

投影方程（内参作用过程） ：

相机坐标系中的点P(X,Y,Z)P(X,Y,Z)P(X,Y,Z)，经内参转换为像素坐标(u,v)(u,v)(u,v)：
1. 无倾斜（θ=90°，理想情况）：
  u=α⋅XZ+u0,v=β⋅YZ+v0u=\alpha\cdot\frac{X}{Z}+u_0,\quad v=\beta\cdot\frac{Y}{Z}+v_0u=α⋅ZX+u0,v=β⋅ZY+v0
  （XZ\frac{X}{Z}ZX、YZ\frac{Y}{Z}ZY为归一化图像坐标，乘以尺度因子α/β转换为像素，再叠加主点偏移(u₀,v₀)）
2. 有倾斜（θ≠90°，实际情况）：
  u=α⋅XZ−αcot⁡θ⋅YZ+u0,v=βsin⁡θ⋅YZ+v0u=\alpha\cdot\frac{X}{Z}-\alpha\cot\theta\cdot\frac{Y}{Z}+u_0,\quad v=\frac{\beta}{\sin\theta}\cdot\frac{Y}{Z}+v_0u=α⋅ZX−αcotθ⋅ZY+u0,v=sinθβ⋅ZY+v0
  （额外引入−αcot⁡θ⋅YZ-\alpha\cot\theta\cdot\frac{Y}{Z}−αcotθ⋅ZY项补偿X/Y轴倾斜的影响）
内参矩阵K ：将上述方程整理为矩阵形式，便于计算：
K=[α−αcot⁡θu00βsin⁡θv0001]K=\begin{bmatrix}\alpha&-\alpha\cot\theta&u_0\\0&\frac{\beta}{\sin\theta}&v_0\\0&0&1\end{bmatrix}K= α00−αcotθsinθβ0u0v01

当θ=90°时，cot⁡θ=0\cot\theta=0cotθ=0、sin⁡θ=1\sin\theta=1sinθ=1，矩阵简化为：
K=[α0u00βv0001]K=\begin{bmatrix}\alpha&0&u_0\\0&\beta&v_0\\0&0&1\end{bmatrix}K= α000β0u0v01

（对角矩阵，理想内参）

2. 外参（Extrinsic Parameters）：相机的"外在姿态"

外参描述相机在世界坐标系中的位置与姿态，连接"世界坐标系"与"相机坐标系"，共6个参数（3个旋转+3个平移）。

外参类型	符号	维度	核心作用	关键特性
旋转矩阵	R	3×3	描述相机姿态（绕X/Y/Z轴旋转）	正交矩阵，满足RTR=IR^TR=IRTR=I（转置等于逆），行列式为1（右手坐标系）
平移向量	t	3×1	描述相机位置（相对世界原点）	向量分量(tx,ty,tz)(t_x,t_y,t_z)(tx,ty,tz)分别为相机原点在世界X/Y/Z轴上的偏移量

坐标变换方程（外参作用过程） ：
世界坐标系中的点WP(XW,YW,ZW)^W P(X_W,Y_W,Z_W)WP(XW,YW,ZW)，经外参转换为相机坐标系中的点CP(XC,YC,ZC)^C P(X_C,Y_C,Z_C)CP(XC,YC,ZC)：
1. 纯平移（仅位置变化，姿态不变）：
  CP=WP+t^C P=^W P + tCP=WP+t
  （相机原点相对于世界原点偏移t，所有点的坐标均叠加t）
2. 纯旋转（仅姿态变化，位置不变）：
  CP=R⋅WP^C P=R\cdot^W PCP=R⋅WP
  （绕X/Y/Z轴旋转的组合，如先绕X轴转α角，再绕Y轴转β角，最后绕Z轴转γ角）
3. 平移+旋转（完整变换，齐次形式）：
  为统一处理平移与旋转，引入齐次坐标（4维），变换矩阵为"旋转矩阵+平移向量"的组合： $CP1\]=\[Rt0T1\]\[WP1\]\\begin{bmatrix}\^C P\\\\1\\end{bmatrix}=\\begin{bmatrix}R\&t\\\\0\^T\&1\\end{bmatrix}\\begin{bmatrix}\^W P\\\\1\\end{bmatrix}\[CP1\]=\[R0Tt1\]\[WP1$ （0T=(0,0,0)0^T=(0,0,0)0T=(0,0,0)，右下角1为齐次坐标的缩放因子）

3. 最终投影矩阵（世界→像素的完整链路）

结合内参与外参，可推导从"世界坐标"到"像素坐标"的完整映射矩阵------投影矩阵M：

核心公式 ：p=1ZM⋅WPp=\frac{1}{Z}M\cdot^W Pp=Z1M⋅WP

其中：
- p=(u,v,1)Tp=(u,v,1)^Tp=(u,v,1)T：像素的齐次坐标；
- M=K⋅(R t)M=K\cdot(R\ \ t)M=K⋅(R t)：3×4投影矩阵（K为3×3内参矩阵，(R t)为3×4外参矩阵）；
- ZZZ：相机坐标系中的深度值（由Z=m3⋅WPZ=m_3\cdot^W PZ=m3⋅WP计算，m3m_3m3为M的第3行）；
- 1Z\frac{1}{Z}Z1：齐次坐标的归一化因子，消除深度对投影的影响。
物理意义 ：

世界坐标→（外参R,t）→相机坐标→（内参K）→归一化图像坐标→（除以Z）→像素坐标，形成"3D→2D"的完整闭环，是后续"相机标定"（求解内参K与外参R,t）的理论基础。

核心结论与应用价值

投影模型的选择依据：
- 透视投影：适用于近距离、大视场场景（如手机拍照、自动驾驶），需完整考虑透视效应；
- 正交投影：适用于远距离、高精度测量（如卫星地图、工业检测），需消除透视畸变；
- 弱透视投影：适用于小物体、近光轴场景（如显微成像、零件识别），平衡精度与计算量。
参数的核心作用：
- 内参K：决定相机"如何成像"（如焦距、主点位置），需通过相机标定实验求解；
- 外参(R,t)：决定相机"在哪里成像"（如在世界中的位置与朝向），需结合场景特征（如棋盘格）估计；
- 投影矩阵M：整合内参与外参，是"3D重建""目标定位"等任务的核心输入（如通过M反推空间点的3D坐标）。
后续学习关联 ：

本章内容是"相机标定""立体视觉""运动恢复结构（SfM）"的前置基础------相机标定的目标是求解K、R、t；立体视觉需利用两台相机的内参与外参计算深度；SfM需通过多帧图像的投影矩阵恢复场景3D结构。

4.单应性

核心围绕2D单应性变换 展开：先明确单应性是保线、可逆的投影映射 ，2D单应由3×3非奇异矩阵 表示（含8个自由度 ）；随后梳理单应变换层级（从低到高为等距变换3DOF、缩放变换4DOF、仿射变换6DOF、单应变换8DOF）；详解单应估计方法------需至少4对对应点 ，通过构建线性方程（如x′=h11x+h12y+h13h31x+h32y+h33x'=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}}x′=h31x+h32y+h33h11x+h12y+h13），用线性最小二乘（ATAh=ATbA^TAh=A^TbATAh=ATb）或SVD 求解；介绍两大核心应用（全景拼接 ：通过单应融合多图；相机位姿估计 ：结合内参K从单应推导旋转矩阵R和平移向量t）；还补充了透视n点（PnP）问题 （估计相机6DOF位姿，方法含EPnP）及相机标定（分标定板法和自标定法）。

思维导图

详细总结

前置回顾：相机参数与单应引入

文档开篇简要回顾相机参数，明确投影矩阵M=K[Rt]\mathcal{M}=K[R\quad t]M=K[Rt]（KKK为内参，R/tR/tR/t为外参），投影关系为p=1zMPp=\frac{1}{z}\mathcal{M}Pp=z1MP（p=(u,v)Tp=(u,v)^Tp=(u,v)T为像素点，PPP为世界点），为后续单应性与3D位姿估计奠定基础。

单应性（Homography）基础定义

通用定义

单应性是保线、可逆的投影映射 （记为H:Pn→PnH:P^n→P^nH:Pn→Pn），由(n+1)×(n+1)(n+1)×(n+1)(n+1)×(n+1)非奇异矩阵表示，自由度为(n+1)2−1(n+1)^2-1(n+1)2−1（消除尺度歧义）。计算机视觉中重点关注2D单应性 （n=2n=2n=2）。
2D单应性核心特性
- 保线性：3个共线点经单应变换后仍共线；
- 矩阵形式：3×3非奇异矩阵，记为H=[h11h12h13h21h22h23h31h32h33]H=\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix}H= h11h21h31h12h22h32h13h23h33 ；
- 自由度（DOF）：8个（3×3矩阵共9个元素，消除尺度因子后剩8个独立参数）；
- 变换关系：齐次坐标下[x′y′1]∼H[xy1]\begin{bmatrix}x'\\y'\\1\end{bmatrix} \sim H\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′1 ∼H xy1 ，非齐次形式为：
  x′=h11x+h12y+h13h31x+h32y+h33,y′=h21x+h22y+h23h31x+h32y+h33x'=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}},\quad y'=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}x′=h31x+h32y+h33h11x+h12y+h13,y′=h31x+h32y+h33h21x+h22y+h23

单应变换层级（从特殊到一般）

单应变换是最一般的2D投影变换，包含从简单到复杂的4个层级，各层级的矩阵形式、自由度、不变量差异显著，具体对比如下：

变换层级	矩阵形式	自由度（DOF）	核心不变量	适用场景
等距变换	[εcos⁡θ−sin⁡θtxεsin⁡θcos⁡θty001]\begin{bmatrix}\varepsilon\cos\theta&-\sin\theta&t_x\\\varepsilon\sin\theta&\cos\theta&t_y\\0&0&1\end{bmatrix} εcosθεsinθ0−sinθcosθ0txty1 （ε=±1\varepsilon=\pm1ε=±1）	3	长度、角度、面积	刚体运动（如物体平移旋转）
缩放变换	[sr11sr12txsr21sr22ty001]\begin{bmatrix}s r_{11}&s r_{12}&t_x\\s r_{21}&s r_{22}&t_y\\0&0&1\end{bmatrix} sr11sr210sr12sr220txty1 （s为缩放因子）	4	角度	相似变换（如图像缩放+旋转）
仿射变换	[a11a12txa21a22ty001]\begin{bmatrix}a_{11}&a_{12}&t_x\\a_{21}&a_{22}&t_y\\0&0&1\end{bmatrix} a11a210a12a220txty1 （A为非奇异矩阵）	6	平行线、平行长度比、面积比	非均匀缩放（如拉伸图像）
单应变换	[h11h12h13h21h22h23h31h32h33]\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix} h11h21h31h12h22h32h13h23h33	8	直线上四点的交比（Cross Ratio）	透视畸变场景（如全景拼接）

关键补充：交比（Cross Ratio） 是单应变换的核心不变量，定义为直线上四点x1,x2,x3,x4x_1,x_2,x_3,x_4x1,x2,x3,x4的比例关系，即Cross(x1,x2,x3,x4)=(x3−x1)(x4−x2)(x3−x2)(x4−x1)\text{Cross}(x_1,x_2,x_3,x_4)=\frac{(x_3-x_1)(x_4-x_2)}{(x_3-x_2)(x_4-x_1)}Cross(x1,x2,x3,x4)=(x3−x2)(x4−x1)(x3−x1)(x4−x2)，变换后数值不变。

2D单应估计方法（从对应点到求解）

单应估计的核心是通过图像点对应关系求解3×3单应矩阵H，需满足以下条件与步骤：

核心前提

至少需要4对不共线的对应点（每对对应点提供2个方程，8个自由度需8个方程，4对对应点恰好满足）。
估计步骤与方程构建
- 步骤1：设定约束消除尺度歧义
  
  方法1：设h33=1h_{33}=1h33=1（固定矩阵右下角元素为1，减少1个参数），此时非齐次方程可整理为线性形式：
  h11x+h12y+h13−h31xx′−h32yx′=x′h_{11}x + h_{12}y + h_{13} - h_{31}xx' - h_{32}yx' = x'h11x+h12y+h13−h31xx′−h32yx′=x′
  h21x+h22y+h23−h31xy′−h32yy′=y′h_{21}x + h_{22}y + h_{23} - h_{31}xy' - h_{32}yy' = y'h21x+h22y+h23−h31xy′−h32yy′=y′
  
  方法2：设∥h∥=1\|h\|=1∥h∥=1（矩阵元素的L2范数为1），适用于需严格约束尺度的场景。
- 步骤2：形成线性系统
  
  对N对对应点，构建2N×8的矩阵A和2N×1的向量b，形成线性方程组Ah=bAh=bAh=b（方法1）或Ah=0Ah=0Ah=0（方法2）。

求解方法

约束类型	求解算法	核心公式/步骤
无约束（h33=1h_{33}=1h33=1）	线性最小二乘	h=(ATA)−1ATbh=(A^TA)^{-1}A^Tbh=(ATA)−1ATb，Matlab中可直接用h=A\bh=A\backslash bh=A\b求解
有约束（∣h∣=1\|h\|=1∣h∣=1）	SVD分解（奇异值分解）	1. 计算ATAA^TAATA；2. 对ATAA^TAATA做SVD分解得U,D,VTU,D,V^TU,D,VT；3. 取V中最小特征值对应的列向量作为h

超定情况处理

当对应点数N>4时（超定系统），通过最小化投影误差优化H，常用非线性最小二乘方法（如Levenberg-Marquardt算法）。

单应性的核心应用场景

应用1：全景拼接（Panorama Stitching）

目标是将多幅重叠图像融合为一幅宽视角全景图，步骤如下：
1. 图像去畸变：消除镜头畸变（如桶形/枕形畸变），确保后续单应计算准确；
2. 寻找对应点：通过特征检测算法（如SIFT、ORB）匹配多幅图像的重叠区域点；
3. 计算单应H：用4对以上对应点估计相邻图像间的单应矩阵；
4. 重采样与融合 ：
  - 遍历第一幅图像的像素，通过H投影到第二幅图像的对应位置；
  - 用双线性插值填充投影后的像素值，避免锯齿；
  - 融合多幅图像的重叠区域，生成全景图。
应用2：相机位姿估计（Camera Pose Estimation）

目标是通过单应矩阵推导相机的6DOF位姿（3个旋转参数R+3个平移参数t），适用于增强现实（AR）、机器人导航等场景，具体流程：
- 前提条件：已知相机内参矩阵K（需提前标定）、平面场景的单应H；
- 核心推导：
  平面场景中（设Z=0），投影关系为x=K[r1,r2,t]Xx=K[r_1,r_2,t]Xx=K[r1,r2,t]X，对比单应定义得H=λK[r1,r2,t]H=\lambda K[r_1,r_2,t]H=λK[r1,r2,t]（λ为尺度因子）；
  两边左乘K−1K^{-1}K−1，得K−1H=λ[r1,r2,t]K^{-1}H=\lambda[r_1,r_2,t]K−1H=λ[r1,r2,t]，其中r1,r2r_1,r_2r1,r2是旋转矩阵R的前两列（需满足单位正交性）；
- 关键问题解决：
  ① 尺度因子λ不唯一：取r1r_1r1和r2r_2r2对应的λ的平均值；
  ② 旋转矩阵不正交：对初步估计的R′R'R′做SVD分解，令R=UVTR=UV^TR=UVT（U、V为正交矩阵），确保R的正交性；
- 典型案例：标志物跟踪（如Aruco marker），步骤为"视频输入→标志物识别→计算单应→估计3D位姿→渲染虚拟物体并叠加到真实图像"。

透视n点（PnP）问题

PnP是单应位姿估计的扩展，适用于非平面场景，核心是通过3D-2D点对应关系估计相机外参：

问题定义

已知：① 3D物体点的世界坐标Xi=(Xi,Yi,Zi)X_i=(X_i,Y_i,Z_i)Xi=(Xi,Yi,Zi)；② 对应的2D图像点坐标xi=(ui,vi)x_i=(u_i,v_i)xi=(ui,vi)；③ 相机内参K（已标定）；

求解：相机外参------旋转矩阵R（3参数）、平移向量t（3参数），共6个自由度。

常用求解方法

方法名称	核心特点	适用场景
P3P	仅需3对对应点，直接求解，但鲁棒性较差	点少且噪声小的场景
EPnP	O(n)复杂度，OpenCV默认方法，用4个控制点表示所有点	实时场景（如机器人视觉）
DLT	基于直接线性变换，需6对以上对应点	高精度、非实时场景
UPnP	鲁棒性强，适用于噪声较大的对应点数据	复杂环境（如户外导航）

应用案例：Aruco标志物跟踪
1. 准备工作：打印Aruco标志物（如6×6网格），标定相机获取内参K；
2. 流程：
  - 视频输入：通过摄像头采集含标志物的图像；
  - 标志物检测：识别标志物的4个角点（3D-2D对应点）；
  - PnP求解：用EPnP估计相机相对于标志物的位姿（R,t）；
  - 渲染叠加：将虚拟物体（如3D立方体）按位姿渲染，叠加到真实图像。

相机标定（Camera Calibration）

相机标定是求解内参和外参的关键步骤，直接影响单应估计和PnP位姿的精度：

核心目标

求解相机的内参（α,β,u0,v0,θ\alpha,\beta,u_0,v_0,\thetaα,β,u0,v0,θ）和外参（每幅标定图像对应的R,t），消除镜头畸变影响。

方法分类

标定方法	核心特点	优点	缺点
基于标定板	利用已知结构的标定目标（如棋盘格）	精度高，适用于所有相机模型	流程复杂，需高精度标定板
自标定	仅用多幅图像的对应点，无需标定目标	灵活性高，适用无标定板场景	非线性问题，鲁棒性低，易受噪声影响

线性标定流程

以基于棋盘格的标定为例，步骤如下：
1. 拍摄标定板：从不同角度拍摄至少10幅含棋盘格的图像；
2. 识别图像点：自动或手动标记棋盘格的角点（已知世界坐标）；
3. 构建方程 ：根据投影关系u=m1⋅Pm3⋅Pu=\frac{m_1\cdot P}{m_3\cdot P}u=m3⋅Pm1⋅P，v=m2⋅Pm3⋅Pv=\frac{m_2\cdot P}{m_3\cdot P}v=m3⋅Pm2⋅P构建线性方程组；
4. 求解参数 ：
  - 初步求解：用线性最小二乘得到内参和外参的初始值；
  - 优化迭代：用非线性最小二乘（如Gaussian-Newton算法）最小化投影误差，优化参数。

作业任务

Homework1：纯旋转相机场景下，推导并计算单应矩阵H（提示：纯旋转时平移t=0，投影矩阵简化）；
Homework2：给定3cm×3cm网格的图像，用文档介绍的单应估计方法（如4点法+线性最小二乘）计算单应矩阵。

关键问题

单应变换的4个层级（等距、缩放、仿射、单应）在自由度、不变量上有何核心差异？这些差异决定了它们各自的适用场景是什么？

单应变换的4个层级从特殊到一般，自由度、不变量及适用场景差异显著，具体如下：

变换层级	自由度（DOF）	核心不变量	适用场景
等距变换	3	长度、角度、面积	刚体运动场景（如机器人抓取物体时的视觉定位，需保持物体尺寸和角度不变）
缩放变换	4	角度	相似变换场景（如图像缩放+旋转，需保持物体形状不变仅改变大小，如证件照裁剪）
仿射变换	6	平行线、平行长度比、面积比	非均匀缩放场景（如图像拉伸、挤压，需保持平行线关系，如UI设计中的图像变形）
单应变换	8	直线上四点的交比	透视畸变场景（如全景拼接、相机位姿估计，需处理不同视角的透视差异）

核心逻辑：层级越一般（如单应），自由度越高，不变量越少，适用场景越复杂（如透视畸变）；层级越特殊（如等距），自由度越低，不变量越多，适用场景越简单（如刚体运动）。

估计2D单应矩阵H需要多少对对应点？为什么？当对应点数超过所需数量时，如何处理超定系统以提高H的精度？

所需对应点数 ：至少4对不共线的对应点 。

原因：2D单应矩阵H是3×3非奇异矩阵，共9个元素，但存在1个尺度歧义（即kH与H表示同一单应，k≠0），因此实际自由度为8个；每对对应点（(x,y)(x,y)(x,y)与(x′,y′)(x',y')(x′,y′)）可提供2个线性方程（从非齐次投影公式推导），8个自由度需8个方程，故需4对对应点（4×2=8个方程）。
超定系统处理（对应点数N>4） ：

当对应点数超过4时，系统为超定（方程数2N>8），此时需通过最小化投影误差优化H，常用方法如下：
- 第一步：用线性最小二乘求解初始H，公式为h=(ATA)−1ATbh=(A^TA)^{-1}A^Tbh=(ATA)−1ATb（A为2N×8矩阵，b为2N×1向量）；
- 第二步：用非线性最小二乘优化，如Levenberg-Marquardt算法，目标函数为最小化所有对应点的投影误差（即真实图像点与H投影得到的预测点之间的欧氏距离）；
- 核心目的：消除噪声对对应点的影响，使估计的H更符合实际投影关系，提高后续应用（如全景拼接、位姿估计）的精度。

如何利用单应矩阵H估计相机的6DOF位姿（R,t）？推导过程中会遇到哪些关键问题？如何解决这些问题？

位姿估计的前提与推导过程：
- 前提：① 场景为平面（设世界坐标系中平面Z=0）；② 已知相机内参矩阵K（需提前标定）；③ 已估计出平面场景的单应矩阵H。
- 核心推导：
  平面场景的投影关系为x=K[r1,r2,t]Xx=K[r_1,r_2,t]Xx=K[r1,r2,t]X（r1,r2r_1,r_2r1,r2为旋转矩阵R的前两列，t为平移向量）；
  对比单应矩阵的定义（x=HXx=HXx=HX），可得H=λK[r1,r2,t]H=\lambda K[r_1,r_2,t]H=λK[r1,r2,t]（λ为尺度因子）；
  两边左乘K−1K^{-1}K−1，得K−1H=λ[r1,r2,t]K^{-1}H=\lambda[r_1,r_2,t]K−1H=λ[r1,r2,t]，由此可分离出r1,r2,tr_1,r_2,tr1,r2,t的初步估计（除以λ）。

推导中的关键问题与解决方案：

关键问题	产生原因	解决方案
尺度因子λ不唯一	r1r_1r1和r2r_2r2从K−1HK^{-1}HK−1H分离时，λ可能不同	计算r1r_1r1和r2r_2r2对应的λ（如λ1=∣K−1H\lambda_1=\|K^{-1}Hλ1=∣K−1H的第1列\|，λ2=∣K−1H\lambda_2=\|K^{-1}Hλ2=∣K−1H的第2列\|），取两者的平均值作为最终λ
初步估计的旋转矩阵不正交	噪声或对应点误差导致r1⋅r2≠0r_1\cdot r_2≠0r1⋅r2=0或∣r1∣≠1\|r_1\|≠1∣r1∣=1	对初步旋转矩阵R′=[r1,r2,r1×r2]R'=[r_1,r_2,r_1×r_2]R′=[r1,r2,r1×r2]做SVD分解得R′=UVTR'=UV^TR′=UVT，令R=UVTR=UV^TR=UVT（U、V为正交矩阵），确保R满足正交性（RTR=IR^TR=IRTR=I）

最终位姿确定 ：

旋转矩阵R的第三列r3=r1×r2r_3=r_1×r_2r3=r1×r2（叉乘），平移向量t由t=1λ⋅(K−1Ht=\frac{1}{\lambda}\cdot(K^{-1}Ht=λ1⋅(K−1H的第3列)计算，最终得到相机的6DOF位姿（R,t），可用于增强现实（AR）中虚拟物体的叠加。

5.相机标定

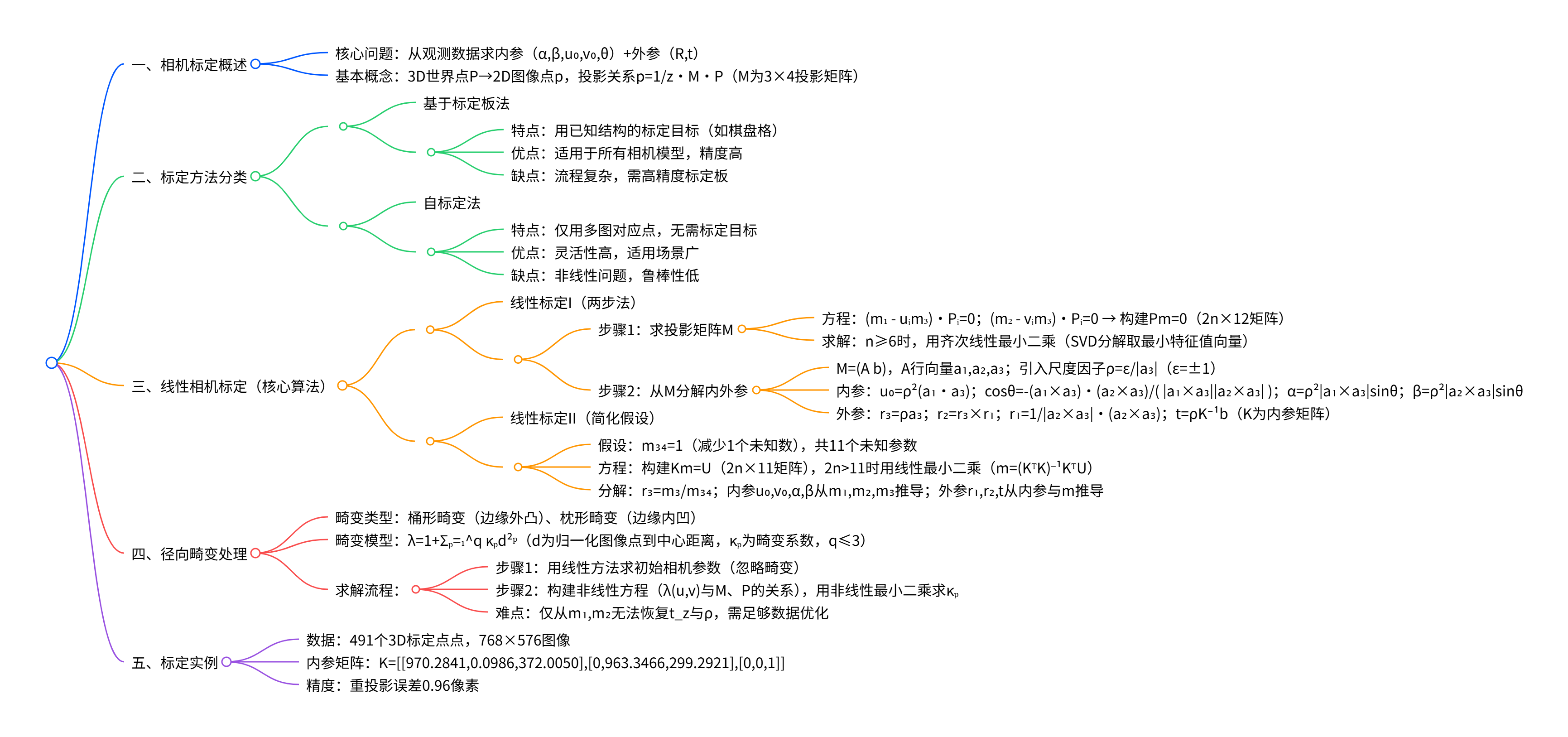
核心目标是通过观测数据求解相机内参（α,β,u₀,v₀,θ） 与外参（旋转矩阵R、平移向量t） ；首先将标定方法分为基于标定板法 （高精度、需已知场景结构）与自标定法 （灵活、非线性鲁棒性低）两类；重点阐述线性标定两步法（先通过线性最小二乘求解3×4透视投影矩阵M，再从M分解内外参，需至少6个3D-2D对应点），并补充线性标定II（假设m₃₄=1简化求解）；还详细说明径向畸变（桶形/枕形）的建模（λ=1+Σκₚd²ᵖ，κₚ为畸变系数）与非线性求解流程；最后给出标定实例（内参矩阵、重投影误差0.96像素），完整覆盖相机标定的问题定义、方法分类、核心算法及误差处理。

思维导图

详细总结

相机标定核心定义与问题

核心目标

通过相机拍摄的3D世界点P（已知坐标） 与对应的2D图像点p（观测坐标），求解相机的两类关键参数：
- 内参：描述相机光学/电学特性，包括尺度因子α（x方向）、β（y方向）、主点坐标(u₀,v₀)、轴夹角θ（理想90°）；
- 外参：描述相机在世界坐标系中的姿态，包括旋转矩阵R（3×3正交矩阵）、平移向量t（3×1向量）。
投影关系基础

3D点到2D点的投影通过3×4透视投影矩阵M 实现，齐次坐标下公式为：
z[uivi1]=M[PixPiyPiz1]z\begin{bmatrix}u_i\\v_i\\1\end{bmatrix}=M\begin{bmatrix}P_{ix}\\P_{iy}\\P_{iz}\\1\end{bmatrix}z uivi1 =M PixPiyPiz1

其中z为3D点在相机坐标系中的深度，M可分解为内参矩阵K与外参矩阵[R t]的乘积，即M=K[Rt]M=K[R\quad t]M=K[Rt]。

相机标定方法分类

两类方法在原理、精度、适用场景上差异显著，具体对比如下：

标定方法	核心特点	优点	缺点	适用场景
基于标定板法	依赖已知结构的标定目标（如棋盘格、3D标定 rig）	1. 适用于所有相机模型； 2. 标定精度高	1. 流程复杂（需多角度拍摄）； 2. 对标定板精度要求高	高精度场景（如工业检测、3D重建）
自标定法	仅利用多幅图像间的点对应关系，无需标定目标	1. 灵活性高； 2. 无需预设场景结构	1. 非线性优化问题； 2. 鲁棒性低（易受噪声影响）	无标定板场景（如户外导航、动态场景）

线性相机标定算法（核心内容）

文档详细介绍两种线性标定思路，均通过"构建线性方程→求解投影矩阵M→分解内外参"实现，核心差异在于M的求解约束不同。

1. 线性标定I（标准两步法）

适用于无特殊假设的场景，需至少6个3D-2D对应点（n≥6），步骤如下：

步骤	核心任务	方程/算法	关键细节
1	构建线性方程组	对每个对应点(i)，由投影关系推导： (m1−uim3)⋅P⃗i=0(m_1 - u_i m_3)·\vec{P}_i = 0(m1−uim3)⋅P i=0 (m2−vim3)⋅P⃗i=0(m_2 - v_i m_3)·\vec{P}_i = 0(m2−vim3)⋅P i=0	堆叠n个点的方程，形成2n×12的矩阵P和12×1的向量m（M的元素），得到齐次方程Pm=0Pm=0Pm=0
2	求解投影矩阵M	齐次线性最小二乘：对P做SVD分解，取PTPP^TPPTP最小特征值对应的特征向量作为m	M为3×4矩阵，需满足单位Frobenius范数（\|m\|=1）
3	从M分解内外参	设M=(Ab)M=(A\quad b)M=(Ab)（A为3×3矩阵，b为3×1向量），引入尺度因子ρ=ε/	a₃
4	计算内参	- u0=ρ2(a1⋅a3)u_0=ρ²(a₁·a₃)u0=ρ2(a1⋅a3)（主点x坐标） - $cosθ=-(a₁×a₃)·(a₂×a₃)/(	a₁×a₃
5	计算外参	- 旋转矩阵R：$r₁=1/	a₂×a₃

2. 线性标定II（简化假设法）

通过假设m34=1m_{34}=1m34=1（M第3行第4列元素为1）减少未知数，步骤如下：

简化约束 ：M共12个元素，设m34=1m_{34}=1m34=1后剩11个未知参数，记为m；
构建方程 ：对n个对应点，构建2n×11的矩阵K和2n×1的向量U，形成线性方程组Km=UKm=UKm=U；
求解M ：当2n>11（超定系统）时，用线性最小二乘求解m=(KTK)−1KTUm=(K^TK)^{-1}K^TUm=(KTK)−1KTU，进而构建M；
分解参数 ：
- 旋转矩阵：r3=m3/m34r₃=m₃/m_{34}r3=m3/m34（m₃为M第3行前3个元素）；r1=(m1−u0m3)⋅m34/αr₁=(m₁ - u₀m₃)·m_{34}/αr1=(m1−u0m3)⋅m34/α；r2=(m2−v0m3)⋅m34/βr₂=(m₂ - v₀m₃)·m_{34}/βr2=(m2−v0m3)⋅m34/β；
- 平移向量：tx=(m14−u0)⋅m34/αt_x=(m_{14} - u₀)·m_{34}/αtx=(m14−u0)⋅m34/α；ty=(m24−v0)⋅m34/βt_y=(m_{24} - v₀)·m_{34}/βty=(m24−v0)⋅m34/β；tz=m34t_z=m_{34}tz=m34。

四、径向畸变处理（误差补偿）

镜头制造缺陷会导致径向畸变（边缘光线投影偏差），文档重点介绍其建模与求解：

畸变类型
- 桶形畸变（Barrel）：图像边缘向外凸；
- 枕形畸变（Pin Cushion）：图像边缘向内凹；
- 无畸变（理想镜头，仅理论存在）。
畸变模型

假设图像中心为主点（u₀=v₀=0），畸变通过缩放因子λ修正，λ为归一化距离d²（图像点到中心距离的平方）的多项式：
λ=1+∑p=1qκpd2p\lambda=1+\sum_{p=1}^q \kappa_p d^{2p}λ=1+p=1∑qκpd2p

其中：
- q≤3（低次多项式，避免过拟合）；
- κₚ为径向畸变系数（需求解的未知量）；
- d2=u^2+v^2d²=\hat{u}^2+\hat{v}^2d2=u^2+v^2（u^,v^\hat{u},\hat{v}u^,v^为归一化图像坐标，由物理坐标与内参转换得到）。
求解流程
- 步骤1：忽略畸变，用线性标定求解初始内参（K）与外参（R,t）；
- 步骤2：构建非线性方程：λ[uv]=1m3⋅P[m1⋅Pm2⋅P]\lambda\begin{bmatrix}u\\v\end{bmatrix}=\frac{1}{m_3·P}\begin{bmatrix}m_1·P\\m_2·P\end{bmatrix}λ[uv]=m3⋅P1[m1⋅Pm2⋅P]，代入λ模型；
- 步骤3：用非线性最小二乘（如Levenberg-Marquardt算法）优化κₚ、t_z、ρ（仅从m₁,m₂无法恢复t_z，需足够数据约束）。

标定实例（验证效果）

文档给出具体标定案例，验证算法有效性：

标定数据：491个3D标定点点（来自标定rig），对应768×576分辨率图像的2D点；
内参矩阵 ：
K=[970.28410.0986372.00500963.3466299.2921001]K=\begin{bmatrix}970.2841&0.0986&372.0050\\0&963.3466&299.2921\\0&0&1\end{bmatrix}K= 970.2841000.0986963.34660372.0050299.29211
标定精度 ：重投影误差（真实2D点与M投影点的欧氏距离）为0.96像素，精度满足多数计算机视觉场景需求。

关键问题

基于标定板法与自标定法在原理、精度、适用场景上有何核心差异？选择时需优先考虑哪些因素？

两类方法的核心差异如下表，选择时需优先考虑"精度需求""场景约束""流程复杂度"：

对比维度	基于标定板法	自标定法
原理	利用已知结构的标定目标（如棋盘格），构建3D-2D对应关系	仅利用多幅图像间的点对应关系，无需预设场景结构
精度	高（标定板结构已知，误差可控）	低（非线性优化易受噪声影响，鲁棒性差）
流程复杂度	复杂（需多角度拍摄标定板，确保点覆盖全视场）	简单（仅需采集多幅重叠图像）
适用场景	高精度需求场景（工业检测、3D重建、AR位姿估计）	无标定板场景（户外导航、动态场景、无法布置标定目标的环境）

选择因素：若场景允许布置标定板且需高精度（如工业零件尺寸测量），优先选基于标定板法；若场景动态或无法预设标定目标（如无人机户外飞行），则选自标定法。

线性标定I的核心步骤是"求解投影矩阵M→分解内外参"，请详细说明M的求解方程如何构建，以及从M分解内参（u₀,α,θ）的关键公式与逻辑。

投影矩阵M的求解方程构建 ：

对每个3D-2D对应点(i)，由投影关系ui=m1⋅P⃗im3⋅P⃗iu_i=\frac{m_1·\vec{P}_i}{m_3·\vec{P}_i}ui=m3⋅P im1⋅P i、vi=m2⋅P⃗im3⋅P⃗iv_i=\frac{m_2·\vec{P}_i}{m_3·\vec{P}_i}vi=m3⋅P im2⋅P i（m₁,m₂,m₃为M的行向量），整理得齐次方程：
(m1−uim3)⋅P⃗i=0(m_1 - u_i m_3)·\vec{P}_i = 0(m1−uim3)⋅P i=0
(m2−vim3)⋅P⃗i=0(m_2 - v_i m_3)·\vec{P}_i = 0(m2−vim3)⋅P i=0

对n个点，堆叠上述方程形成2n×12的矩阵P （每行对应1个方程，列对应M的12个元素）和12×1的向量m （M的元素），最终得到齐次线性系统Pm=0Pm=0Pm=0。当n≥6时，通过SVD分解PTPP^TPPTP，取最小特征值对应的特征向量作为m，即M的元素。
从M分解内参（u₀,α,θ）的关键公式与逻辑：
- 步骤1：拆分M为M=(Ab)M=(A\quad b)M=(Ab)（A为3×3矩阵，a₁,a₂,a₃为A的行向量），引入尺度因子ρ=ϵ/∣a3∣\rho=\epsilon/|a_3|ρ=ϵ/∣a3∣（ε=±1，确保α,β为正，|a₃|为a₃的L2范数）；
- 步骤2：求主点u₀：利用旋转矩阵行向量的正交性（r₁·r₃=0），推导得u0=ρ2(a1⋅a3)u_0=\rho²(a₁·a₃)u0=ρ2(a1⋅a3)；
- 步骤3：求轴夹角θ：θ为相机X/Y轴的夹角，利用r₁与r₂的正交性，推导得cosθ=−(a1×a3)⋅(a2×a3)∣a1×a3∣⋅∣a2×a3∣cosθ=-\frac{(a₁×a₃)·(a₂×a₃)}{|a₁×a₃|·|a₂×a₃|}cosθ=−∣a1×a3∣⋅∣a2×a3∣(a1×a3)⋅(a2×a3)（叉乘确保向量垂直于a₃，对应r₁,r₂的方向）；
- 步骤4：求x尺度因子α：α为焦距与像素水平尺寸的比值，利用r₁的单位性（|r₁|=1），推导得α=ρ2∣a1×a3∣sinθα=ρ²|a₁×a₃|sinθα=ρ2∣a1×a3∣sinθ（sinθ由θ的余弦值计算，因θ接近90°，sinθ为正）。

径向畸变会导致图像边缘偏差，如何建立畸变模型？求解畸变系数κₚ时面临的核心难点是什么？如何解决？

径向畸变模型的建立 ：

文档采用多项式缩放模型 修正畸变，核心思路是：畸变图像点(u,v)由无畸变点(u^,v^\hat{u},\hat{v}u^,v^)经缩放因子λ修正得到，即(u,v)=λ(u^,v^)(u,v)=\lambda(\hat{u},\hat{v})(u,v)=λ(u^,v^)，其中λ为归一化距离d²（无畸变点到图像中心的距离平方）的低次多项式：
λ=1+∑p=1qκpd2p\lambda=1+\sum_{p=1}^q \kappa_p d^{2p}λ=1+p=1∑qκpd2p

式中：
- q≤3（避免过拟合，通常取q=1或2）；
- κₚ为待求解的径向畸变系数；
- d2=u^2+v^2d²=\hat{u}^2+\hat{v}^2d2=u^2+v^2（u^,v^\hat{u},\hat{v}u^,v^为无畸变的归一化图像坐标，由物理坐标与内参转换：u^=uα+vcosθβ\hat{u}=\frac{u}{\alpha}+\frac{v cosθ}{\beta}u^=αu+βvcosθ，v^=vsinθ∣β∣\hat{v}=\frac{v sinθ}{|\beta|}v^=∣β∣vsinθ）。
求解κₚ的核心难点与解决方法：
- 核心难点：仅通过m₁（M第1行）和m₂（M第2行）无法同时恢复尺度因子ρ、平移分量t_z和畸变系数κₚ------因畸变模型引入非线性项（λ中的d²ᵖ），且t_z的信息仅存在于M的第3行（m₃），而m₃未参与初始线性求解（仅用m₁,m₂构建方程）。
- 解决方法 ：
  1. 两步法优化：先忽略畸变，用线性标定求解初始内参（K）、外参（R,r₃）；
  2. 非线性最小二乘：构建目标函数（最小化"畸变修正后的投影点"与"真实图像点"的误差），代入λ模型和M的投影关系，联合优化κₚ、ρ、t_z；
  3. 数据约束：采集足够多的3D-2D对应点（n≥8），形成超定系统，确保非线性优化有唯一解（如文档中用491个标定点点，保证精度）。

6.相机标定II

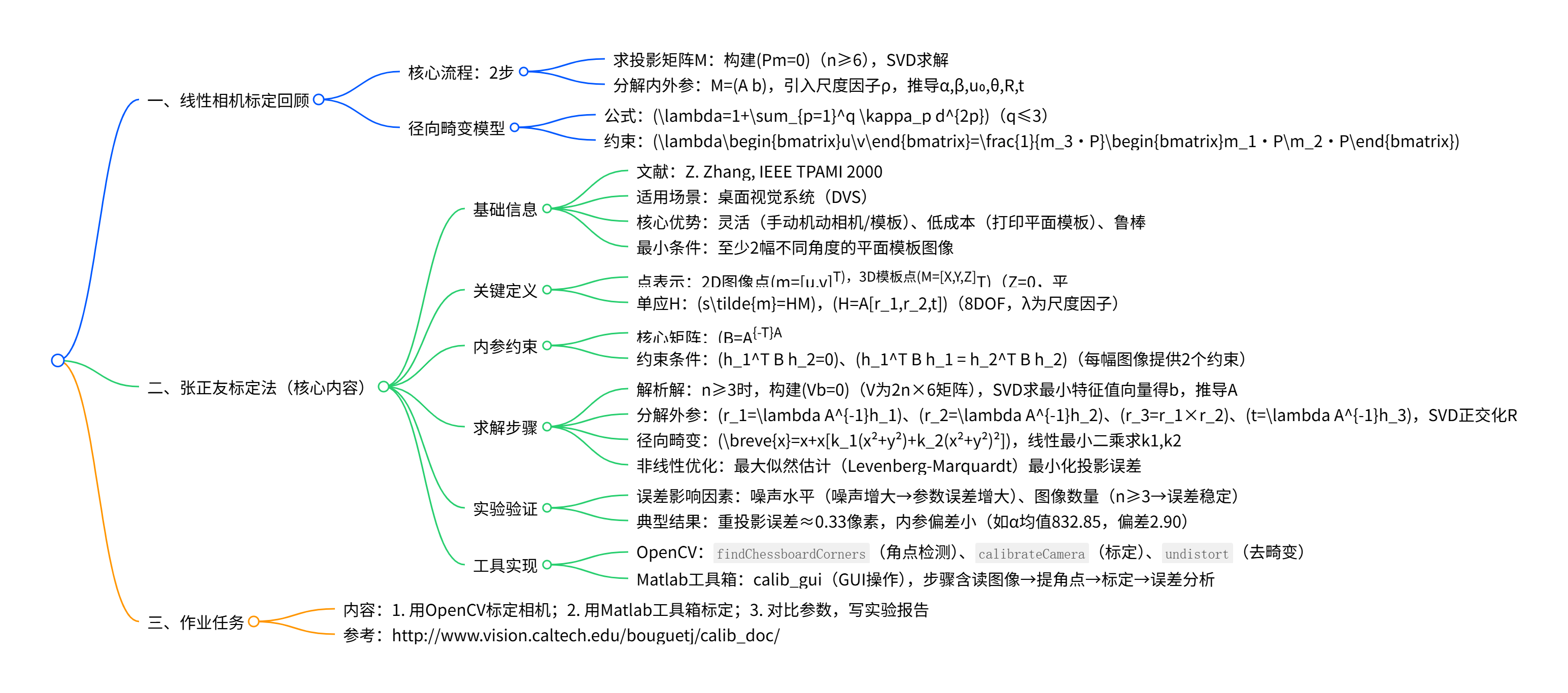
先回顾线性相机标定的两步流程（求解透视投影矩阵M→分解内外参）及径向畸变模型（λ=1+∑p=1qκpd2p\lambda=1+\sum_{p=1}^q \kappa_p d^{2p}λ=1+∑p=1qκpd2p）；随后详细阐述张正友方法的核心------仅需相机观测至少2个不同角度的平面模板 ，通过建立"平面模板与图像间的单应H"，利用内参约束（h1TA−TA−1h2=0h_1^T A^{-T} A^{-1} h_2=0h1TA−TA−1h2=0、h1TA−TA−1h1=h2TA−TA−1h2h_1^T A^{-T} A^{-1} h_1 = h_2^T A^{-T} A^{-1} h_2h1TA−TA−1h1=h2TA−TA−1h2）求解内参矩阵A（含α,β,u₀,v₀,γ），再分解外参（R,t），并通过非线性最大似然估计（Levenberg-Marquardt算法） 优化参数；还介绍了该方法的实验验证（噪声水平与图像数量对误差的影响）、工具实现（OpenCV函数如calibrateCamera、Matlab标定工具箱）。

思维导图

详细总结

线性相机标定回顾（前置知识）

线性标定核心流程（两步法）
- 步骤1：求解透视投影矩阵M
  对n个3D-2D对应点，构建齐次线性方程组Pm=0Pm=0Pm=0（P为2n×12矩阵，m为M的12个元素），当n≥6 时，通过SVD分解PTPP^TPPTP，取最小特征值对应的特征向量作为m，得到3×4的M。
- 步骤2：分解内外参
  将M拆分为M=(Ab)M=(A\quad b)M=(Ab)（A为3×3矩阵，b为3×1向量），引入尺度因子ρ=ϵ/∣a3∣\rho=\epsilon/|a_3|ρ=ϵ/∣a3∣（ε=±1，a₃为A的第3行），利用旋转矩阵的正交性（RTR=IR^TR=IRTR=I）推导内参（α,β,u₀,θ）和外参（R,t）。
径向畸变模型回顾

镜头畸变用缩放因子λ修正，λ为归一化距离d²的低次多项式：
λ=1+∑p=1qκpd2p\lambda=1+\sum_{p=1}^q \kappa_p d^{2p}λ=1+p=1∑qκpd2p

其中：q≤3（避免过拟合），d2=u2α2+v2β2+2uvαβcosθd²=\frac{u²}{\alpha²}+\frac{v²}{\beta²}+2\frac{uv}{\alpha\beta}cosθd2=α2u2+β2v2+2αβuvcosθ（u,v为图像点坐标），约束关系为λ[uv]=1m3⋅P[m1⋅Pm2⋅P]\lambda\begin{bmatrix}u\\v\end{bmatrix}=\frac{1}{m_3·P}\begin{bmatrix}m_1·P\\m_2·P\end{bmatrix}λ[uv]=m3⋅P1[m1⋅Pm2⋅P]。

张正友标定法（核心章节）

张正友标定法是文档重点，发表于2000年IEEE TPAMI期刊，是计算机视觉中应用最广泛的标定方法之一，具体内容分模块详解：

1. 方法基础与优势

维度	具体内容
适用场景	桌面视觉系统（DVS），如工业检测、机器人视觉
核心特点	1. 灵活性：相机或平面模板可手动机动，无需精密设备； 2. 低成本：模板可打印在平面上； 3. 鲁棒性：抗噪声能力强，超定系统优化
最小条件	至少拍摄2幅不同角度的平面模板图像（n≥3时内参有唯一解）
模板要求	平面结构（如棋盘格），已知模板点的世界坐标（通常设Z=0，简化计算）

2. 关键定义与单应性

点的表示 ：
- 2D图像点：m=[u,v]Tm=[u,v]^Tm=[u,v]T，齐次形式m~=[u,v,1]T\tilde{m}=[u,v,1]^Tm~=[u,v,1]T；
- 3D模板点：M=[X,Y,Z]TM=[X,Y,Z]^TM=[X,Y,Z]T（因模板平面，设Z=0），齐次形式M~=[X,Y,0,1]T\tilde{M}=[X,Y,0,1]^TM~=[X,Y,0,1]T。
单应矩阵H ：
平面模板与其图像间存在单应关系，满足sm~=HM~s\tilde{m}=H\tilde{M}sm~=HM~（s为尺度因子），且H=A[r1,r2,t]H=A[r_1,r_2,t]H=A[r1,r2,t]------A为内参矩阵，r1,r2r_1,r_2r1,r2为旋转矩阵R的前两列，t为平移向量。
H为3×3矩阵，含8个自由度（消除尺度歧义）。

3. 内参约束与求解

张正友方法的核心是利用旋转矩阵的正交性，建立内参的约束条件：

核心矩阵B ：定义B=A−TA−1B=A^{-T}A^{-1}B=A−TA−1，B为3×3对称矩阵，仅含6个独立参数 （b=[B₁₁,B₁₂,B₂₂,B₁₃,B₂₃,B₃₃]^T），与内参的关系如下：
B=[1α2−γα2βv0γ−u0βα2β−γα2βγ2α2β2+1β2−γ(v0γ−u0β)α2β2−v0β2v0γ−u0βα2β−γ(v0γ−u0β)α2β2−v0β2(v0γ−u0β)2α2β2+v02β2+1]B=\begin{bmatrix}\frac{1}{\alpha²}&-\frac{\gamma}{\alpha²\beta}&\frac{v₀\gamma - u₀\beta}{\alpha²\beta}\\-\frac{\gamma}{\alpha²\beta}&\frac{\gamma²}{\alpha²\beta²}+\frac{1}{\beta²}&-\frac{\gamma(v₀\gamma - u₀\beta)}{\alpha²\beta²}-\frac{v₀}{\beta²}\\\frac{v₀\gamma - u₀\beta}{\alpha²\beta}&-\frac{\gamma(v₀\gamma - u₀\beta)}{\alpha²\beta²}-\frac{v₀}{\beta²}&\frac{(v₀\gamma - u₀\beta)²}{\alpha²\beta²}+\frac{v₀²}{\beta²}+1\end{bmatrix}B= α21−α2βγα2βv0γ−u0β−α2βγα2β2γ2+β21−α2β2γ(v0γ−u0β)−β2v0α2βv0γ−u0β−α2β2γ(v0γ−u0β)−β2v0α2β2(v0γ−u0β)2+β2v02+1
约束条件 ：
因r1Tr2=0r_1^T r_2=0r1Tr2=0且r1Tr1=r2Tr2=1r_1^T r_1=r_2^T r_2=1r1Tr1=r2Tr2=1，代入H=λA[r1,r2,t]H=\lambda A[r_1,r_2,t]H=λA[r1,r2,t]（λ为尺度因子），推导得：
1. h1TBh2=0h_1^T B h_2=0h1TBh2=0（r₁与r₂正交）；
2. h1TBh1=h2TBh2h_1^T B h_1 = h_2^T B h_2h1TBh1=h2TBh2（r₁与r₂模长相等）。
  （h1,h2h_1,h_2h1,h2为H的前两列）
解析解求解 ：
对n幅图像，每幅图像提供2个约束，构建2n×6的矩阵V和方程Vb=0Vb=0Vb=0：
- 当n≥3 时，V为超定矩阵，对VTVV^TVVTV做SVD分解，取最小特征值对应的特征向量作为b；
- 当n=2时，需额外施加无畸变约束（γ=0）；
- 当n=1时，仅能求解α,β（需已知u₀,v₀且γ=0）。
  由b推导内参的公式如下：
  {v0=B12B13−B11B23B11B22−B122λ=B33−B132+v0(B12B13−B11B23)B11α=λB11β=λB11B11B22−B122γ=−B12α2βλu0=γv0α−B13α2λ \begin{cases} v₀=\frac{B₁₂B₁₃ - B₁₁B₂₃}{B₁₁B₂₂ - B₁₂²} \\ \lambda=B₃₃ - \frac{B₁₃² + v₀(B₁₂B₁₃ - B₁₁B₂₃)}{B₁₁} \\ \alpha=\sqrt{\frac{\lambda}{B₁₁}} \\ \beta=\sqrt{\frac{\lambda B₁₁}{B₁₁B₂₂ - B₁₂²}} \\ \gamma=-\frac{B₁₂\alpha²\beta}{\lambda} \\ u₀=\frac{\gamma v₀}{\alpha} - \frac{B₁₃\alpha²}{\lambda} \end{cases} ⎩ ⎨ ⎧v0=B11B22−B122B12B13−B11B23λ=B33−B11B132+v0(B12B13−B11B23)α=B11λ β=B11B22−B122λB11 γ=−λB12α2βu0=αγv0−λB13α2

4. 外参分解与优化

外参分解 ：
已知A和H，由H=λA[r1,r2,t]H=\lambda A[r_1,r_2,t]H=λA[r1,r2,t]推导：
r1=λA−1h1,r2=λA−1h2,r3=r1×r2,t=λA−1h3r_1=\lambda A^{-1}h_1,\quad r_2=\lambda A^{-1}h_2,\quad r_3=r_1×r_2,\quad t=\lambda A^{-1}h_3r1=λA−1h1,r2=λA−1h2,r3=r1×r2,t=λA−1h3
因噪声影响，初步得到的R可能不正交，需通过SVD分解（R′=UVTR'=UV^TR′=UVT）正交化。
径向畸变处理 ：
设理想图像点为(u,v)，实际观测点为(u˘,v˘\breve{u},\breve{v}u˘,v˘)，归一化坐标为(x,y)，畸变模型为：
x˘=x+x[k1(x2+y2)+k2(x2+y2)2],y˘=y+y[k1(x2+y2)+k2(x2+y2)2]\breve{x}=x+x[k_1(x²+y²)+k_2(x²+y²)²],\quad \breve{y}=y+y[k_1(x²+y²)+k_2(x²+y²)²]x˘=x+x[k1(x2+y2)+k2(x2+y2)2],y˘=y+y[k1(x2+y2)+k2(x2+y2)2]
代入u˘=u0+αx+γy\breve{u}=u₀+\alpha x+\gamma yu˘=u0+αx+γy、v˘=v0+βy\breve{v}=v₀+\beta yv˘=v0+βy，构建线性方程组Dk=dDk=dDk=d（D为2mn×2矩阵，k=[k₁,k₂]^T），用线性最小二乘求解k=(DTD)−1DTdk=(D^TD)^{-1}D^Tdk=(DTD)−1DTd。
非线性优化 ：
通过最大似然估计 （Levenberg-Marquardt算法）最小化投影误差，目标函数为：
∑i=1n∑j=1m∥m˘ij−m(A,k1,k2,Ri,ti,Mj)∥2\sum_{i=1}^n\sum_{j=1}^m \|\breve{m}{ij} - m(A,k₁,k₂,R_i,t_i,M_j)\|²i=1∑nj=1∑m∥m˘ij−m(A,k1,k2,Ri,ti,Mj)∥2
（m˘ij\breve{m}{ij}m˘ij为第i幅图像第j个点的观测值，m(·)为投影计算值）

5. 实验验证结果

文档给出实验数据，验证方法的稳定性与精度：

实验指标	结果示例
内参稳定性	α均值832.85（偏差2.90），β均值832.90（偏差2.84），u₀均值304.18（偏差0.44）
径向畸变系数	k₁均值-0.229（偏差0.001），k₂均值0.190（偏差0.006）
重投影误差	均值0.334像素（偏差0.04）
噪声影响	噪声从0→1.6像素，参数误差逐渐增大（如α误差从0→0.8）
图像数量影响	图像数从1→17，参数误差从1.0→0.2（n≥3后误差稳定）

6. 工具实现（OpenCV与Matlab）

OpenCV关键函数：

函数名	功能
`findChessboardCorners`	检测棋盘格角点，返回角点坐标
`calibrateCamera`	输入3D模板点、2D图像点，输出内参矩阵、畸变系数、旋转向量（rvecs）、平移向量（tvecs）
`undistort`	用标定得到的内参和畸变系数，对图像去畸变
`initCameraMatrix2D`	初始化内参矩阵

Matlab标定工具箱操作步骤：
1. 下载工具箱：http://www.vision.caltech.edu/bouguetj/calib_doc/，添加到Matlab路径；
2. 运行calib_gui，选择"Standard"模式；
3. 读取图像：输入图像basename（如Image）和格式（如tif）；
4. 提取角点：点击"Extract grid corners"，选择图像，手动点击4个角点确定模板范围，输入方格尺寸（如30mm）；
5. 标定：点击"Calibration"，自动完成解析解与非线性优化；
6. 结果分析：查看内参、外参（3D可视化）、重投影误差（彩色编码）。

作业任务

文档布置实践作业，强化标定方法的应用能力：

任务内容 ：
- 用OpenCV编写程序，基于TA提供的图像完成相机标定；
- 用Matlab相机标定工具箱完成同一相机的标定；
- 对比两种方法得到的内参（α,β,u₀,v₀,γ）、畸变系数（k₁,k₂）及重投影误差，撰写实验报告。
参考资源：http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/example.html

关键问题

张正友标定法相比传统线性标定法，核心优势是什么？这些优势使其适用于哪些场景？

张正友标定法相比传统线性标定法，核心优势体现在灵活性、成本、鲁棒性三个维度，具体如下：

灵活性更高 ：传统线性标定需高精度3D标定rig（如多控制点的立体标定板），且需固定相机/标定物；张正友方法仅需平面模板（可打印），相机或模板可手动机动，无需精密设备，适配更多场景；
成本更低：传统方法的3D标定rig价格昂贵，张正友方法的模板可自行打印，硬件成本几乎为零；
鲁棒性更强 ：传统线性标定易受噪声影响（仅线性求解，无优化）；张正友方法通过非线性最大似然估计（Levenberg-Marquardt）优化参数，且引入径向畸变修正，降低噪声干扰，重投影误差可控制在0.3像素左右。

适用场景：桌面视觉系统（DVS），如工业零件检测、机器人手眼协调、AR/VR设备标定、低成本视觉项目（无精密标定设备）等。

张正友标定法中，内参约束条件（h1TBh2=0h_1^T B h_2=0h1TBh2=0、h1TBh1=h2TBh2h_1^T B h_1 = h_2^T B h_2h1TBh1=h2TBh2）是如何基于旋转矩阵的特性推导而来的？

内参约束的推导核心是旋转矩阵的正交性 （riTrj=δijr_i^T r_j=\delta_{ij}riTrj=δij，δ为克罗内克函数，i,j=1,2），具体步骤如下：

单应与内外参的关系 ：

平面模板的单应矩阵H满足H=λA[r1,r2,t]H=\lambda A[r_1,r_2,t]H=λA[r1,r2,t]（λ为尺度因子，A为内参矩阵，r₁,r₂为旋转矩阵R的前两列，t为平移向量），因此H的前两列可表示为h1=λAr1h_1=\lambda A r_1h1=λAr1、h2=λAr2h_2=\lambda A r_2h2=λAr2。
利用旋转矩阵的正交性：
- 正交性1：r1Tr2=0r_1^T r_2=0r1Tr2=0（r₁与r₂垂直）：
  对h1=λAr1h_1=\lambda A r_1h1=λAr1、h2=λAr2h_2=\lambda A r_2h2=λAr2两边左乘A−1A^{-1}A−1，得r1=1λA−1h1r_1=\frac{1}{\lambda} A^{-1} h_1r1=λ1A−1h1、r2=1λA−1h2r_2=\frac{1}{\lambda} A^{-1} h_2r2=λ1A−1h2；
  代入r1Tr2=0r_1^T r_2=0r1Tr2=0，得(A−1h1)T(A−1h2)=0(A^{-1} h_1)^T (A^{-1} h_2)=0(A−1h1)T(A−1h2)=0，即h1T(A−TA−1)h2=0h_1^T (A^{-T} A^{-1}) h_2=0h1T(A−TA−1)h2=0；
  因定义B=A−TA−1B=A^{-T} A^{-1}B=A−TA−1，故约束1为h1TBh2=0h_1^T B h_2=0h1TBh2=0。
- 正交性2：r1Tr1=r2Tr2=1r_1^T r_1=r_2^T r_2=1r1Tr1=r2Tr2=1（r₁与r₂模长均为1）：
  同理，代入r1Tr1=1r_1^T r_1=1r1Tr1=1得(A−1h1)T(A−1h1)=(λ)−2(A^{-1} h_1)^T (A^{-1} h_1)=(\lambda)^{-2}(A−1h1)T(A−1h1)=(λ)−2，代入r2Tr2=1r_2^T r_2=1r2Tr2=1得(A−1h2)T(A−1h2)=(λ)−2(A^{-1} h_2)^T (A^{-1} h_2)=(\lambda)^{-2}(A−1h2)T(A−1h2)=(λ)−2；
  两式相等，即h1T(A−TA−1)h1=h2T(A−TA−1)h2h_1^T (A^{-T} A^{-1}) h_1 = h_2^T (A^{-T} A^{-1}) h_2h1T(A−TA−1)h1=h2T(A−TA−1)h2，故约束2为h1TBh1=h2TBh2h_1^T B h_1 = h_2^T B h_2h1TBh1=h2TBh2。
约束的作用 ：

每幅图像提供2个约束，n幅图像提供2n个约束，通过求解Vb=0Vb=0Vb=0（b为B的6个独立参数），可从单应矩阵中分离出内参（A），避免传统方法需多组3D点的局限。

使用OpenCV和Matlab相机标定工具箱进行标定时，核心操作步骤有哪些？如何对比两种方法的标定结果？

OpenCV标定核心步骤

准备工作 ：
- 采集至少10幅不同角度的棋盘格图像（确保棋盘格覆盖全视场）；
- 定义3D模板点（如棋盘格方格尺寸30mm，设Z=0，生成objPoints=[X,Y,0]objPoints=[X,Y,0]objPoints=[X,Y,0]）。
角点检测 ：
- 对每幅图像，用cv2.findChessboardCorners(image, patternSize, corners)检测棋盘格内角点（如patternSize=(9,6)表示9列6行角点）；
- 用cv2.cornerSubPix亚像素优化角点坐标，提高精度。
相机标定 ：
- 调用cv2.calibrateCamera(objPoints, imgPoints, imgSize, camMatrix, distCoeffs, rvecs, tvecs)：
  - objPoints：3D模板点列表；imgPoints：2D图像角点列表；imgSize：图像分辨率；
  - 输出：camMatrix（内参矩阵）、distCoeffs（畸变系数，如[k₁,k₂,p₁,p₂,k₃]）、rvecs（旋转向量）、tvecs（平移向量）。
结果验证 ：
- 用cv2.projectPoints将3D模板点投影到图像，计算投影点与实际角点的欧氏距离，得到重投影误差。

Matlab工具箱标定核心步骤

工具箱配置 ：
- 下载工具箱（http://www.vision.caltech.edu/bouguetj/calib_doc/），添加到Matlab路径，运行`calib_gui`，选择"Standard"模式。
图像读取 ：
- 点击"Image names"，输入图像basename（如"chess"）和格式（如"jpg"），加载所有标定图像。
角点提取 ：
- 点击"Extract grid corners"，选择所有图像，手动点击棋盘格4个对角点确定模板范围；
- 输入方格尺寸（如30mm），工具箱自动提取亚像素角点。
标定与优化 ：
- 点击"Calibration"，工具箱先计算解析解，再通过非线性优化得到最终内参、畸变系数、外参；
- 点击"Show calib results"查看内参矩阵、畸变系数、重投影误差（彩色编码图）。

结果对比维度

对比维度	对比方法
内参矩阵（A）	对比α（fx）、β（fy）、u₀、v₀、γ的数值差异（如计算绝对误差
畸变系数	对比k₁、k₂（径向畸变）、p₁、p₂（切向畸变）的差异，评估一致性
重投影误差	对比两种方法的平均重投影误差（如OpenCV误差0.35像素，Matlab误差0.33像素），误差越小精度越高
外参一致性	对同一幅图像，对比OpenCV的rvecs/tvecs与Matlab的外参（旋转矩阵/平移向量），通过SVD验证旋转矩阵正交性
去畸变效果	用两种方法的内参和畸变系数，调用`cv2.undistort`（OpenCV）和`undistort`（Matlab）对同一幅畸变图像去畸变，目视对比去畸变后的图像清晰度与边缘一致性